Multiple rogue wave and multiple lump solutions of a(3+1)-dimensional Korteweg-de Vries equation
2021-07-21TIANHongfeiSUNYanfangZHANGHuiqun
TIAN Hongfei,SUN Yanfang,ZHANG Huiqun
(Department of Mathematics and Statistics,Qingdao University,Qingdao 266071,Shandong,China)
Abstract:Based on the Hirota bilinear form,we obtained the multiple rogue wave and multiple lump solutions of a new(3+1)-dimensional Korteweg-de Vries(KdV)equation.The dynamic properities of the multiple rogue wave and multiple lump solutions were discussed and illustrated vividly through graphics.
Key words:(3+1)-dimensional Korteweg-de Vries(KdV)equation;Hirota bilinear form;multiple rogue wave;multiple lump solutions
1 Introduction
Rogue waves have always been an important topic since they can illustrate significant nonlinear wave phenomena in the financial markets[1],the water wave tank[2],Bose-Einstein condensates[3],and other areas in mathematical physics.Rogue wave solution is a kind of local rational solution in space and time.As one type of rogue waves,the lump waves[4−6]also have attracted widespread attention because they can describe that wave phenomena in oceanography[7−8]and nonlinear optics[9−10].In mathematics,lump solutions are analytic rational solutions which are localized in all directions in space.In 2015,the positive quadratic function method[11]was used to construct the lump solutions of Kadomtsev-Petviashvili(KP)equation,which has received the attention of many researchers.Recently,dispersion also plays an important role in such lump solutions[12].Some lump solutions of a combined equation involving three types of nonlinear terms have been researched,and they could be formulated by combing different nonlinearities[13].Whereafter,the single lump solutions to nonlinear partial differential equations were investigated[14−18].Futhermore,the multiple rogue wave solutions have also been extensively studied.Among them,ZHA[19]proposed the symbolic computation approach to construct rogue wave solutions.Then,some multiple rogue wave solutions to(3+1)and(2+1)-dimensional equations have been obtained[20−21],such as(3+1)-dimensional Kadomtsev-Petviashvili I equation[22]and(3+1)-dimensional potential Yu-Toda-Sasa-Fukuyama equation[23].Meanwhile,multiple lump solutions were also widely investigated by long wave limit method[24−25],such as(3+1)-dimensional Jimbo-Miwa equation[26]and(3+1)-dimensional nonlinear evolution equation[27].
In this article,we consider a(3+1)-dimensional Korteweg-de Vries(KdV)equation of the following form:

where u=u(x,y,z,t).Through the transformation u=2(lnf)xx,the corresponding bilinear form of equation(1)is
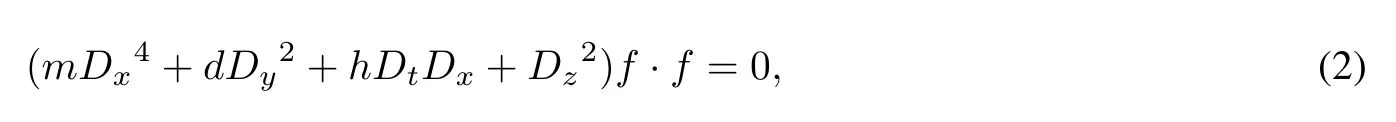
where f=f(x,y,z,t)is the unknown function,d,h,m are real parameters and the derivatives D-operator are the Hirota operators[28]defined by

where p,q,m,n are nonnegative integers.
Whend=1,h=1,m=1,some exact solutions and soliton solutions have been obtained[29].Besides,rational solutions and rogue wave solutions have been constructed[30].Complexiton solutions and dromion-like structures to the KdV equation have been discussed[31−32].Traveling wave solutions for 5th-order KdV type equations with time-dependent coefficients have been studied,too[33].However,multiple rogue wave solutions and multiple lump solutions of equation(1)have not been studied.
The paper aims at studying the multiple rogue wave and multiple lump solutions of a(3+1)-dimensional KdV equation(1).The rest of paper is arranged as follows.In section 2,the multiple rogue wave solutions of reduced equation(1)are obtained via a symbolic computation approach method.In section 3,1-lump,2-lump and 3-lump solutions to equation(1)are discussed.Several conclusions for this paper are given in section 4.
2 Multiple rogue wave solutions
We make the substitution X=x+ξy−dt and reduce the equation(1)to the following(1+1)-dimensional equation
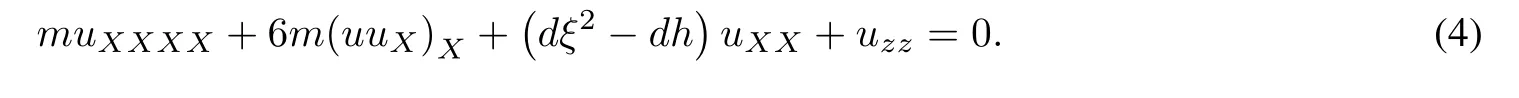
By the transformation

equation(4)is converted into the bilinear equation
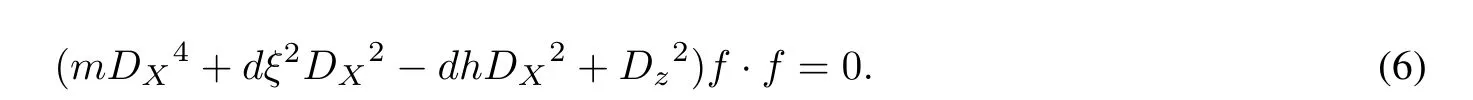
In order to construct multiple rogue wave solutions,we assume the solution has the following form:
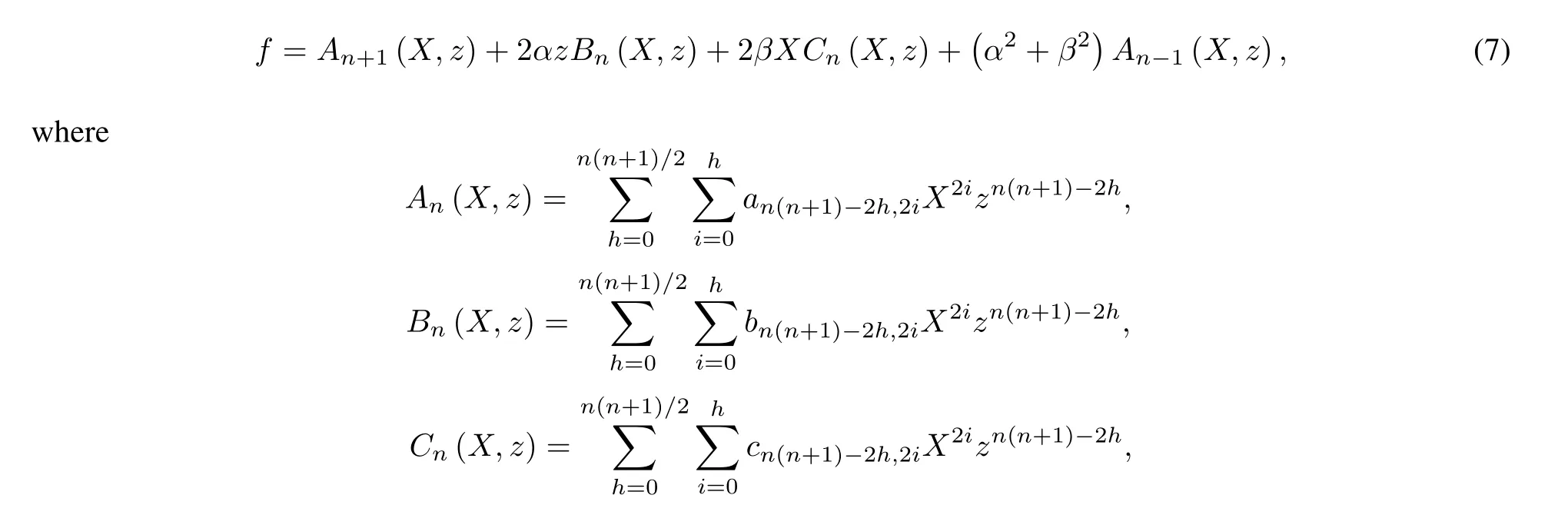
where ai,j,bi,j,ci,j,di,j,i,j∈(0,2,···,n(n+1)/2)are real parameters to be determined,α and β are real parameters to control the center of waves.
2.1 The first order rogue wave solution
In order to obtain the first order rogue wave solution,we choose the following form and set a2,0=1:

Substituting ansatz(8)into equation(6),we obtain the following set of constraining equations for the parameters:
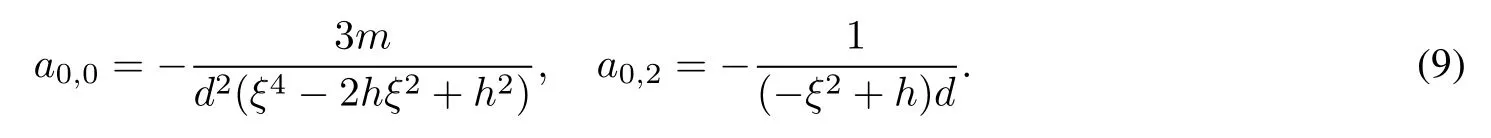
Then we generalize the solution
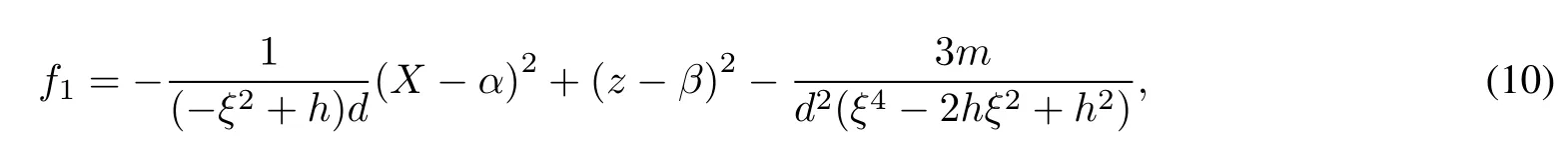
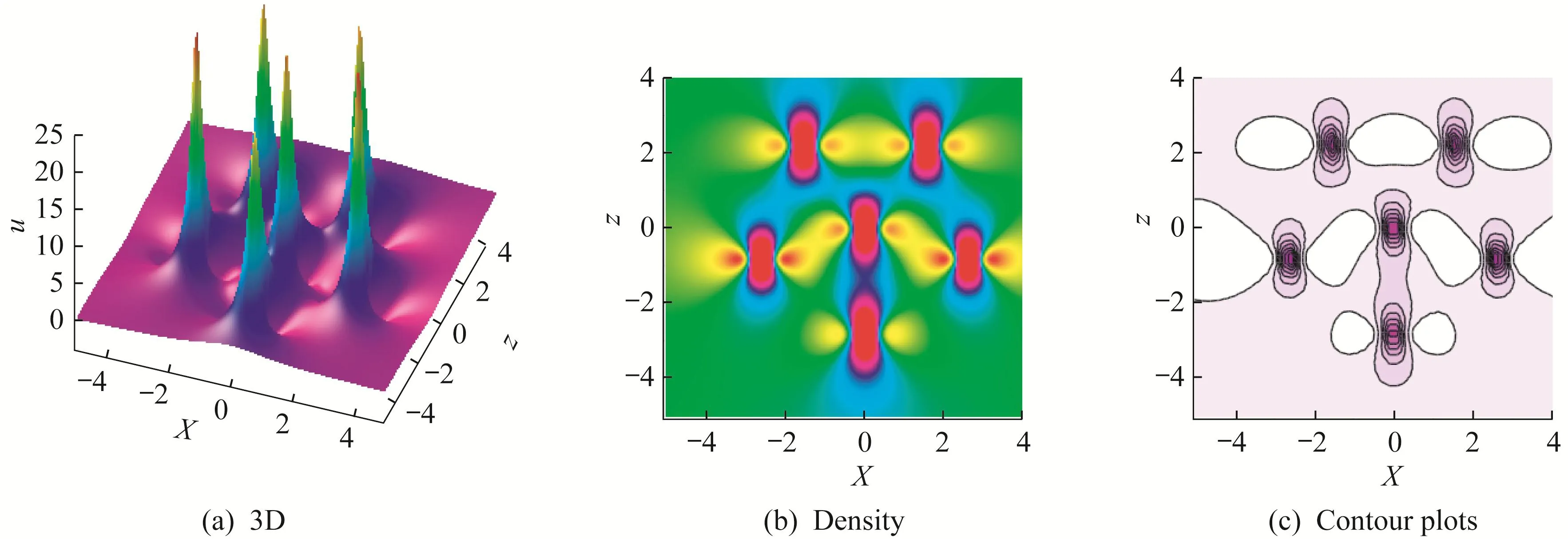
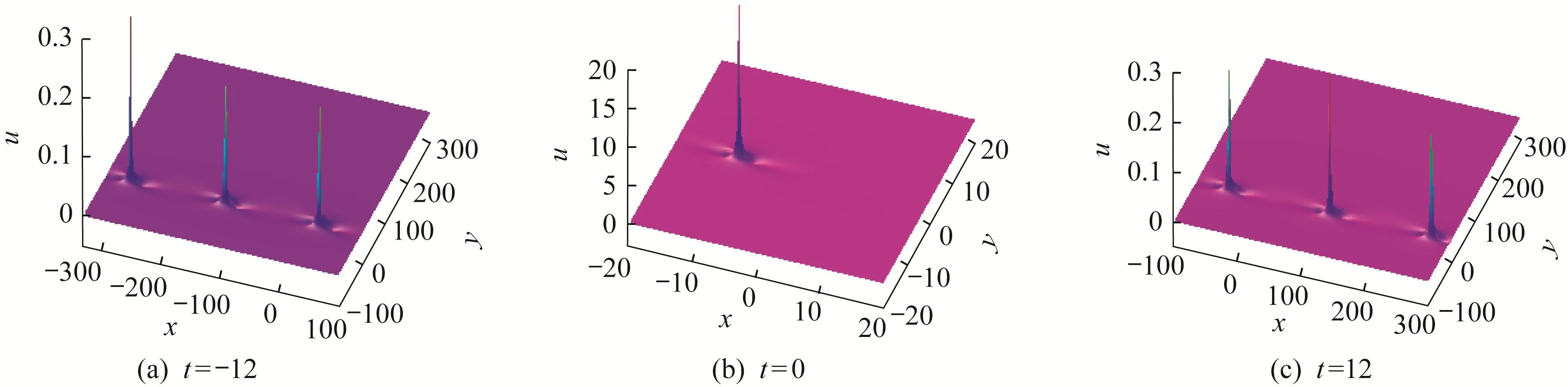
when d<0,m<0,ξ2 The first order rogue wave has the structure for three wave peaks.The maximum and the minimum value of rogue wave are located at{X=α,z=β}and,respectively.The amplitude of the rogue wave is.Futhermore,the center point of rogue wave is related to the value of parameters.For example,one wave is concentrated around(0,0)in figure 1. Figure 1 3D,density and contour plots of the first order rogue wave with α=0,β=0,ξ=1,d=−1,m=−1,h=2 Taking n=1 in ansatz(7)and setting A0(X,z)=1,we get Substituting equation(11)into equation(6),we obtain the following constraint equations for the parameters: By transformation(5),the second order rogue wave solution of equation(4)can be obtained. Taking α=β=0,the peaks of the second order rogue wave solution are concentrated around(0,0).However,when α=β=200,the peaks of rogue wave gradually separate and construct a group of three first order rogue waves which is shown in figure 2. Figure 2 3D,density and contour plots of the second order rogue wave solution with α=200,β=200,ξ=1,d=−1,m=−1 Taking n=2 in ansatz(7),we generalize the solution to the following form: Similarly,we obtain the following set of constraining equations for the parameters: where η=−ξ2+h,and the third order rogue wave solution to equation(4)is obtained. When α=β=1 000,the six peaks of rogue wave gradually separate.The five first order rogue waves are evenly arranged on one regular pentagon,while the rest is at the center of the pentagon as we can see in figure 3. Figure 3 3D,density and contour plots of the first order rogue wave with α=0,β=0,ξ=1,d=−1,m=−1,h=2 In this part,the multiple lump solutions to equation(1)are constructed via long wave limit method.We obtain N-soliton solutions to equation(1)as follows: The first summation in equation(14)represents possible combinations of µ=0 and 1,and the second summation represents possible combinations of the N elements with 1i To obtain the multiple lump solutions to equation(1),we take each ηi0=−1 in equation(14),and get By taking a limit of ki→0 and treating all the kias the same asymptotic order,we change the function fNin equation(16)to the following form: In order to calculate 1-lump solution,we choose N=2 and M=1 in equation(18),then Since the u is invariant when f2is multiplied by constant,we have the simplification to where Bij,θiare given in equation(19). Taking p2=,d=−1,m=0.5 and h=1 in equation(22),we obtain a nonsingular solution, Setting p1=ψ+Ωi,we have Thus,we obtain a 1-lump solution with the condition m>0 and d<0.We see that the solution is decaying as Ofor|x|,|y|,|z|→∞.By choosing appropriate parameters ψ=1 and Ω=1,we show the dynamic behaviors of 1-lump solution in figure 4.During the propagation,we find the amplitude and shape remain the same. Figure 4 Plots of 1-lump wave with x=0 when t=−10,t=0,t=10 In order to calculate 2-lump solution,we choose N=4 and M=2 in equation(18)and it becomes if gure 5,and it describes the interaction of 2-lump waves. where Bijand θiare given in equation(19).Through the transformation u=2(lnf4)xx,a nonsingular 2-lump solution is obtained when p3=p1∗=1+i,p4=p2∗=1+3i with Bij>0.The 2-lump solution is shown in Figure 5 Plots of 2-lump wave with z=10 when t=−3,t=0,t=3 In order to calculate 3-lump solution,we choose N=6 and M=3 in equation(18),where Bijand θiare given in equation(19).Under the transformation u=2(lnf)xx,a nonsingular 3-lump solution is obtained when+3i with Bij>0.The 3-lump solution is shown in if gure 6,and it describes the interaction of three lump waves. Figure 6 Plots of 3-lump wave with z=10 when t=−12,t=0,t=12 Based on the Hirota method,the multiple rogue wave solutions and multiple lump solutions of a(3+1)-dimensional KdV equation were obtained and discussed with symbolic computation approach.With the aid of symbolic calculations,the correctness of the results in this work has been verified.The first,second and third order rogue wave solutions satisfy the property thatu=u0.By implementing the long wave limit,we analyzed the dynamic properties of multiple lump solutions under specific parameter constraints. The research on the partial differential equations with multiple rogue wave solutions is a meaningful and interesting topic.We can pay more attention to discuss bright,dark and Gaussons optical solutions[34].At the same time,we are also paying more attention to N-soliton solutions of integrable equations and analyze the Hirota N-soliton conditions in future[35].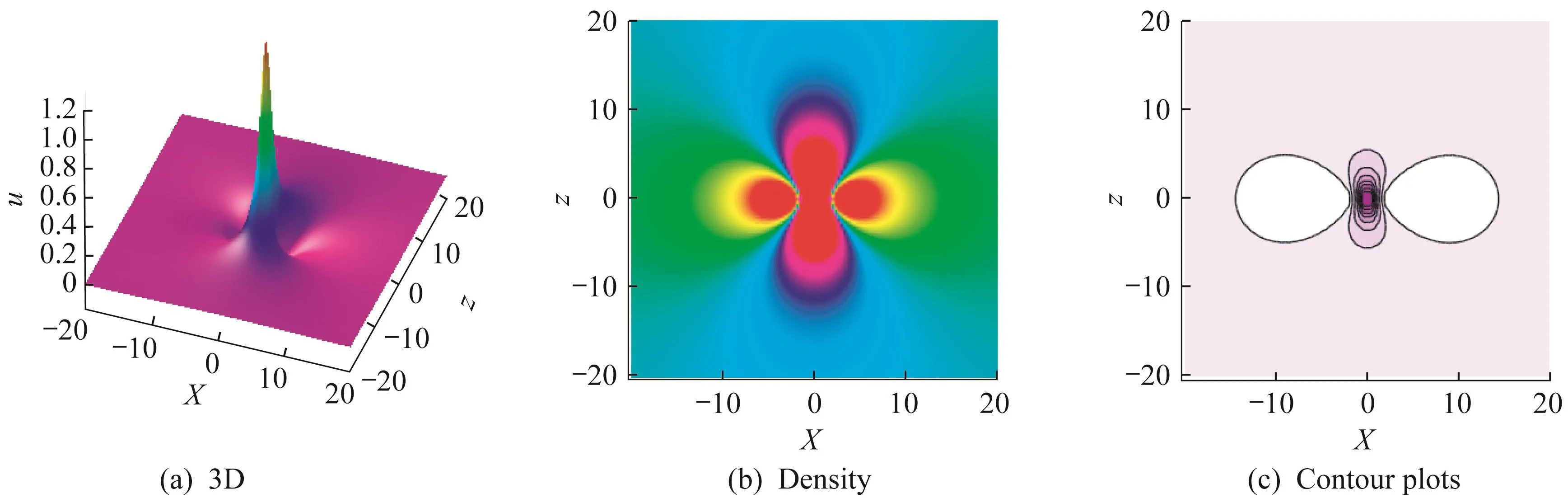
2.2 The second order rogue wave solution

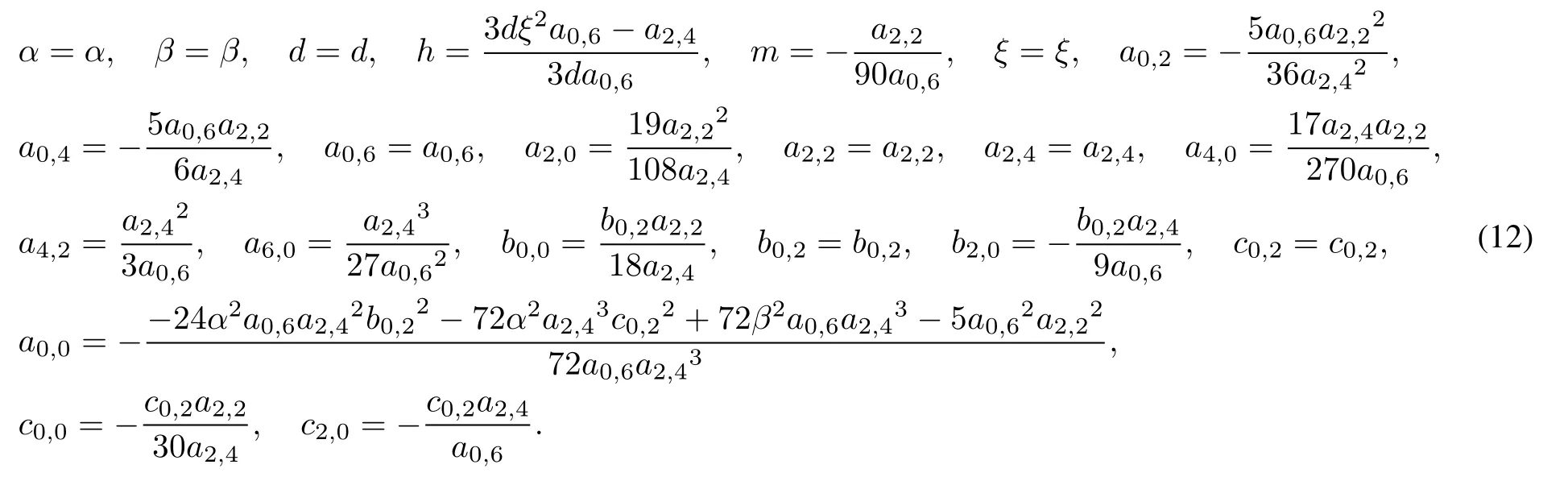

2.3 The third order rogue wave solution



3 Multiple lump solutions

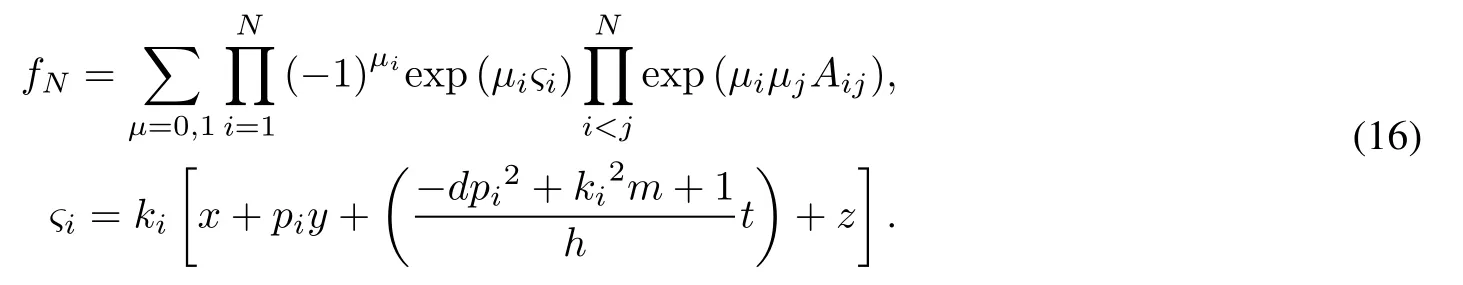
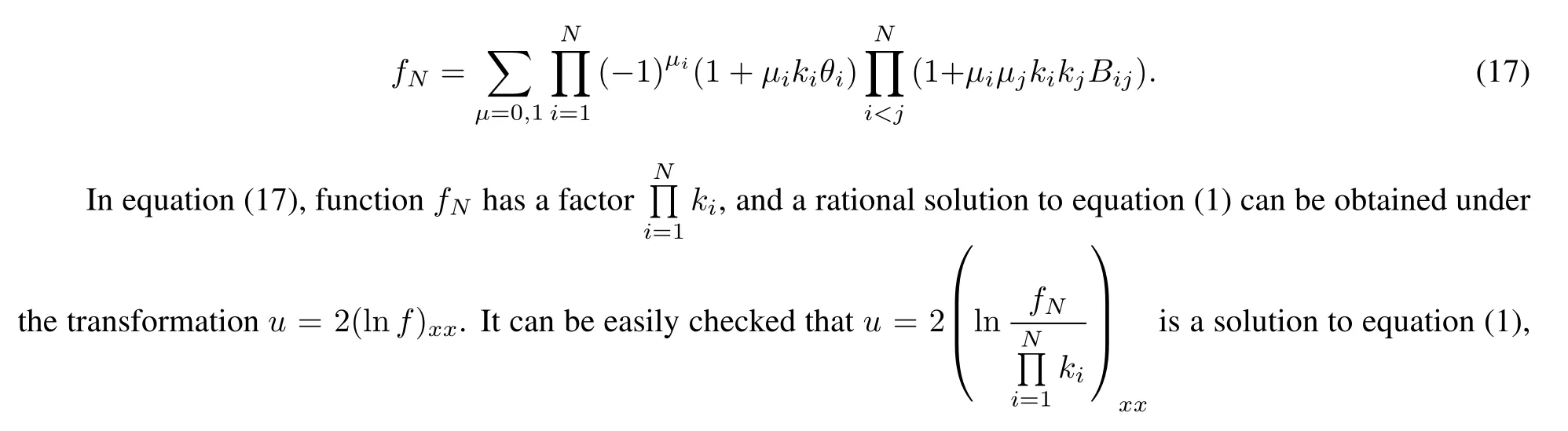

3.1 1-lump solutions
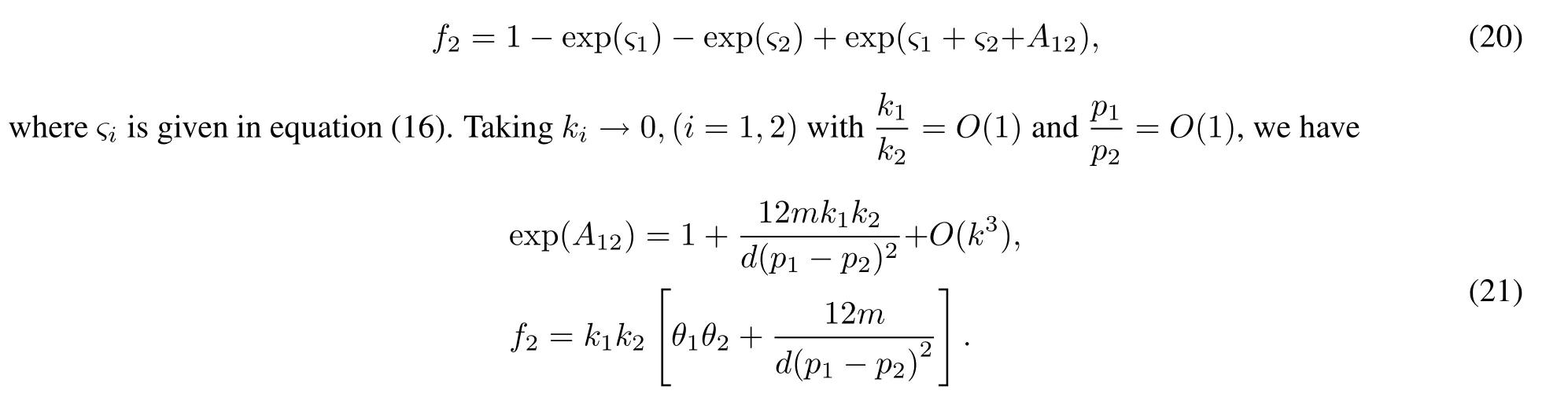

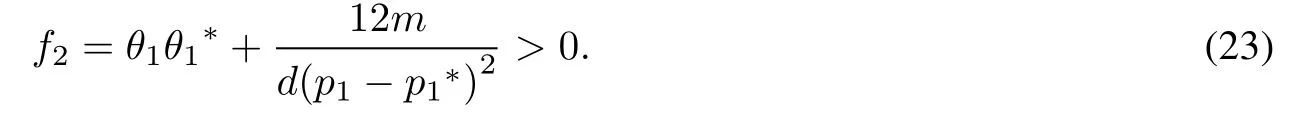


3.2 2-lump solutions
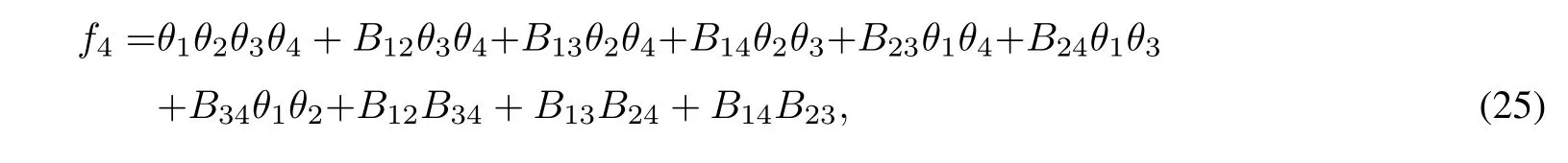
3.3 3-lump solutions
4 Conclusions
杂志排行
上海师范大学学报·自然科学版的其它文章
- Asymptotic stability of linear multistep methods and Runge-Kutta methods for homogeneous differential-algebraic equations with rectangular coefficients
- A spectral method for Burgers equation using Jacobi polynomial
- A graph-theoretic approach to topology identification of stochastic multi-group models with multiple dispersal
- Reflection ordering in the imprimitive complex reflection group G(m,p,n)
- Anti-periodic solution for fuzzy differential equations
- Generalization of existence theorems of root and its application
