Asymptotic stability of linear multistep methods and Runge-Kutta methods for homogeneous differential-algebraic equations with rectangular coefficients

SUN Leping

(Mathematics and Science College,Shanghai Normal University,Shanghai 200234,China)

Abstract:This paper is concerned with the asymptotic stability of numerical methods applied to linear differential-algebraic equations.The coefficient matrices of the system are constant rectangular matrices.We consider linear multistep methods and Runge-Kutta methods applied to the system.The stability results are established under Kronecker canonical form of the original system.

Key words:rectangular coefficient matrix;differential-algebraic equations;asymptotic stability;pencil;Kronecker canonical form

1 Introduction

Differential-algebraic equations(DAEs),which have algebraic constraints,can be found in a wide variety of real worldapplications[1−3].Duringthe periodof time,muchworkhas been donein the field of numericaltreatments applied to linear square differential-algebraic equations Ax+Bx=f,where A,B∈Rn×nare constant matrices andA is singular[4−8].With the development of science and technology,system with rectangular coefficient matrices,A,B∈Rm×n,mn appears more frequently in real world problems,for example,population reproduction,electrical circuits and impulsive behaviors,controlling systems,etc[9−11].

In 1980,CAMPBELL[12]studied DAEs with rectangular coefficient matrices.Based on the theory of singular matrix pencils he obtained conditions under which the system has a unique solution.Then he gave closed solution expressions for these systems.The two kinds of rectangular systems are called one-to-one systems whose coefficients are overdetermined matrices,and on-to systems whose coefficients are underdetermined matrices,respectively.In 1997,DEMMEL[13]discussed the same rectangular DAE model.Applying Kronecker canonical form theory,the model is transformed into four independent blocks,one for each kind in the Kronecker form.Two of them are square subsystems,the other two are overdetermined subsystem and underdetermined subsystem respectively.Therefore,the original model is converted into four subsystems.By studying each subproblem,people can investigate the original problem.

In this paper,we are concerned with asymptotic stability of numerical methods for linear DAEs with constant rectangular coefficients.We will study the DAE model from[13],

2 The Kronecker canonical form of rectangular DAEs

Theorem 1The square system Ax(t)+Bx(t)=0 is solvable if and only if the matrix pencil(A,B),or λA+B is regular,i.e.,not identically singular for any λ.Here λ is called a singular value of λA+B.

The definition of asymptotic stability of its null solution is in the following.

Theorem 2[6]The null solution of square DAE system Ax(t)+Bx(t)=0 is asymptotically stable if and only if all singular values of the matrix pencil(A,B)have negative real part.

The following theorem is related to Kronecker canonical form with regard to a singular matrix pencil.The matrix pencil(λA+B)is singular if either A and B are nonsquare or it is square and det(λA+B)=0 for all values of λ.

Theorem 3[13]Let A and B be arbitrary rectangular m-by-n matrices.Then there are nonsingular matrices P and Q such that λA+B and λPAQ+PBQ are called equivalent and have the same singular values.

The next theorem is called Kronecker canonical form of a singular matrix pencil λA+B which is crucial to our study.

Theorem 4[13]Let A and B be arbitrary rectangular matrices.Then there are nonsingular matrices P and Q such that λPAQ+PBQ is block diagonal with four kinds of blocks:

Now we consider linear differential-algebraic equations(1),whereis a singular pencil.According to the theorem[6],there are square nonsingular matrices P and Q,such that(1)is transformed to

which could be decomposed into four independent block subsystems as follows,here y(t)=Q−1x(t).

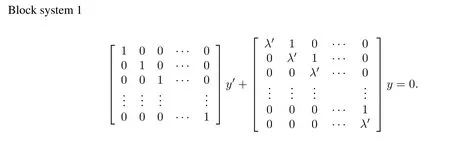
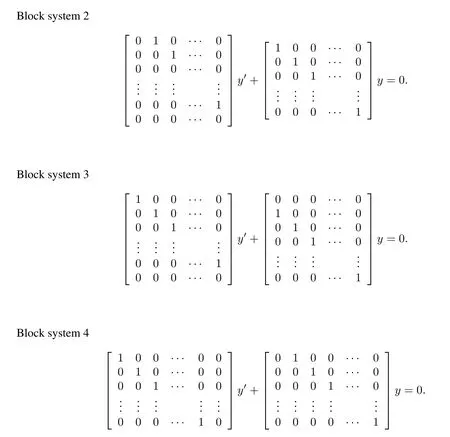
In the next section,we are going to deal with differential-algebraic equations(1)in terms of block system 1–4.The numerical stability analysis of the original system(1)can be obtained via four block systems,eg.,if a numerical method applied to them is asymptotically stable,then the method is asymptotically stable for the original system(1).

3 Stability analysis of BDF methods

In this section,we will consider the asymptotic stability of linear multistep method applied to four subsystems.Without loss of generality,we write four subsystems as following:

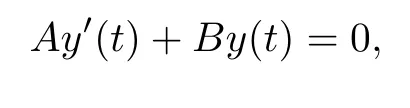
dimension of the coefficient matrices varies according to different subsystem.

Consider multistep method(2),

(I) When(2)is applied to block system 1,we have

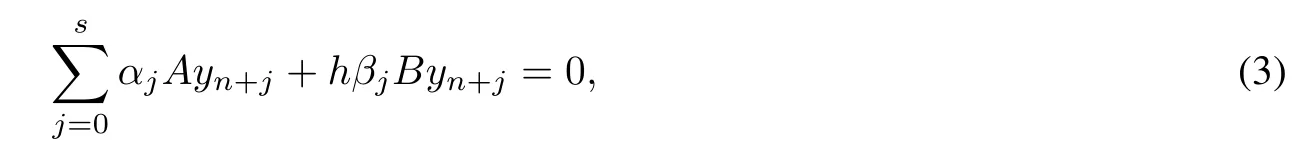
where A is a unit matrix ofm×m,B is an upper triangular matrix with singular value of (A,B)on its maindiagonal.If αsA+hβsB is nonsingular,(3)is solvable.This can be ensured by requiring αsβs0 and βs0,provided if block system 1 is assumed to satisfy the asymptotic stability condition of theorem 2.

Now we will discuss the stability of(3).Consider its characteristic polynomial

(II) When(2)is applied to block system 2,we get(3),where A is an upper triangular matrix with zeros on its main diagonal,B is a unit matrix.

Similar to that in(I),we consider its characteristic polynomial

(III) Now consider block system 3.We see that it is an overdetermined system of(m+1)×m.Theory about its solution refers to[12]in the following theorem.

Theorem 5Suppose(µA+B)is one-to-one for some µ and x is a solution to Ax+Bx=0.Then x is a solution to the square system=0,here

The notation(µA+B)†is the unique Moore-Penrose inverse of µA+B.And all solutions of Ax+Bx=0 are of the form

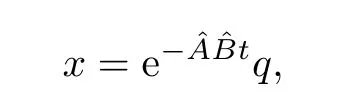
In theorem 5,“one-to-one”means for some µ, µA+B is overdeterminedand its columns are linearly independent.It can be seen that µA+B of our block system 3 is overdetermined of(m+1)×m and the rank of µA+B is m for any µ.We chose a one-to-one matrix pencil(µA+B)for some µ,so that

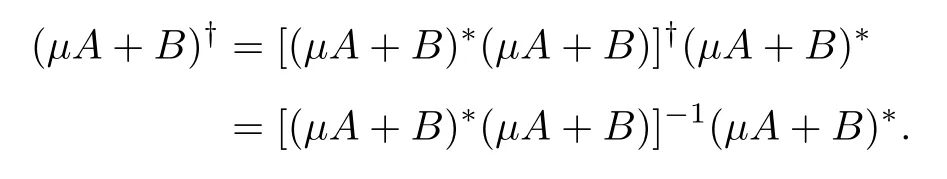
Thus our problem regarding system 3 is reduced to study

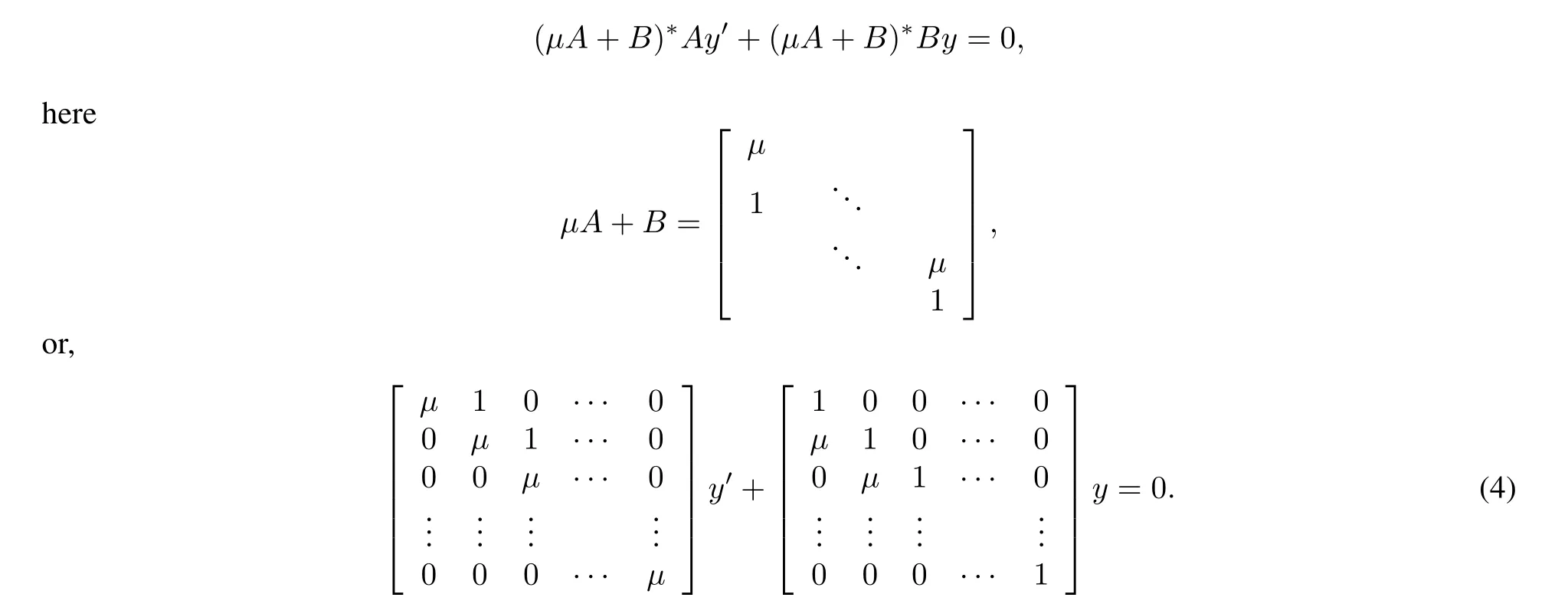
According to the possible values of µ,we have two cases: µ=0 and µ0.

(i) µ=0.It can be seen that in this case,equation(4)has the same structure as block system 2.So we get the characteristic equation as in(II),that is,

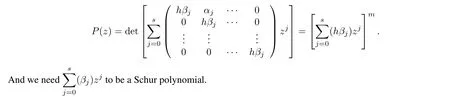
Since ai0,we have

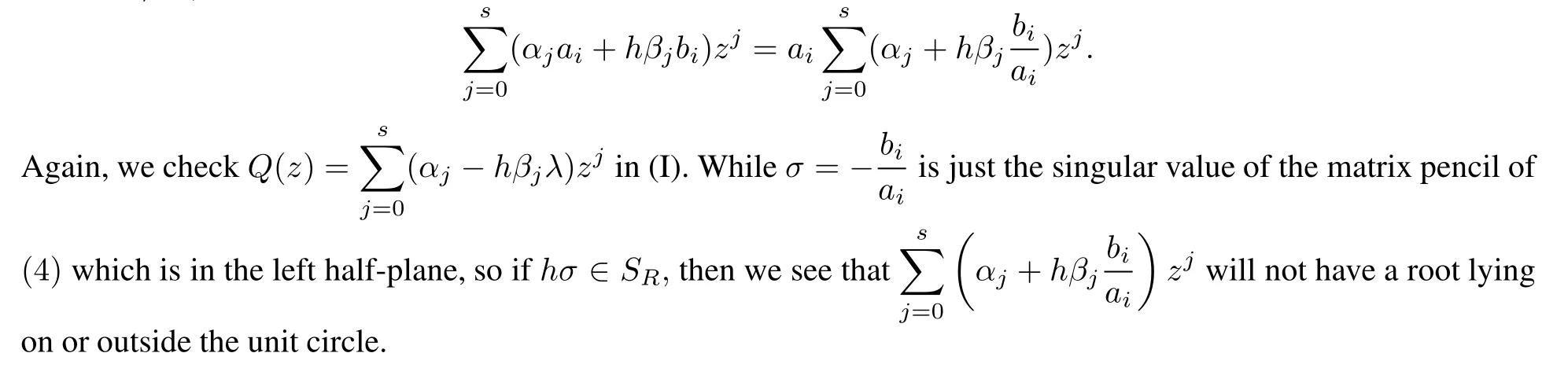
(IV)Consider system 4.It is an underdet ermined system of m×(m+1).The rank of(µA+B)is m.

Theorem 6[12]Suppose that µA+B is onto for some µ.Let=A(µA+B)†,=B(µA+B)†.Define P=(µA+B)†(µA+B).If x is a solution of Ax+Bx=0,then x is the solution of a square system

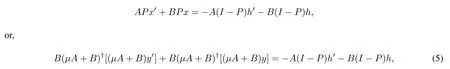
where h is an arbitrary(m+1)-times differentiable vector valued function.

According to theorem6,the equation(5)is in terms of(µA+B)y and has a solution forany choice of(I−P)y.By a simple computation,

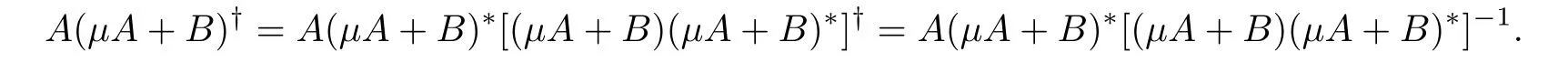
Substitute A and B from block system 4,we get

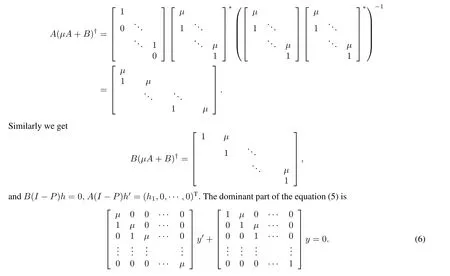
For the sake of convenience,we still take(µA+B)y as y and treat(6)as Ay+By=0.We thus just need to study(6)according to two cases: µ=0 and µ0.

(i) µ=0.Similar to the discussion in subsystem 3,we study the stability by considering the following characteristic polynomial,

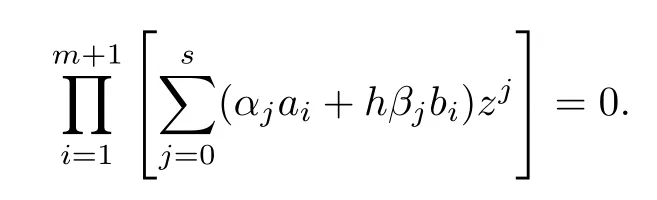
Thus according to the analysis in(I)-(IV)and theorem 5 and theorem 6,we have shown the following result.

Theorem7The multistep method (2) is asymptotically stable for asymptotically stable DAEs(1)ifis a Schur polynomial and hλ∈SRfor all singular values λ of(1)where SRis the stability region of method(2).

In the next section,we will consider Runge-Kutta methods applied to(1)in terms of block system 1 and block system 2.Block system 3 and block system 4 are directly replaced by(4)and(6)respectively.

4 Stability analysis of Runge-Kutta methods

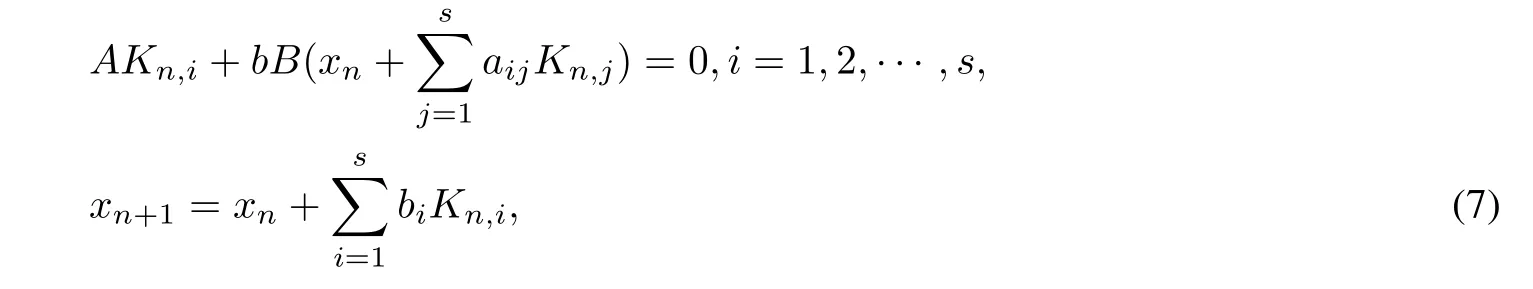
where Kn,i=,i=1,2,···,s are the stage derivatives multiplied by h.As in section 3,we are going to study the asymptotic stability of RK methods applied to the previous four block systems.

(I) Applying(7)to block system 1,we get

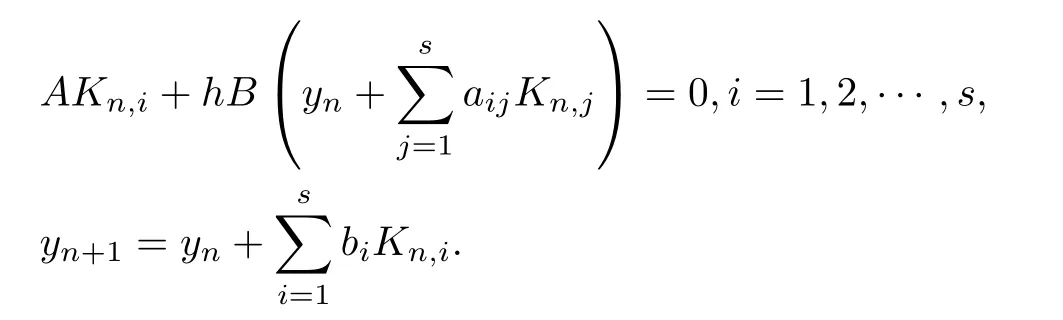
Rearranging the elements of the stage derivatives

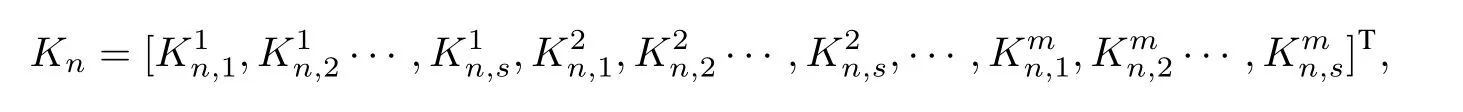
we can write the above difference system as

whereR=(aij)and b=[b1,b2,···,bs]Tdefine the RK method and e=[1,1,···,1].

We consider our problem in terms of the characteristic polynomial of(8),

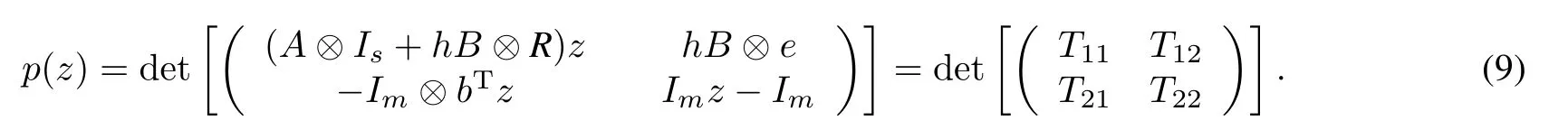
We need the conditions under which the function(9)will have all its roots inside the unit circle.Equivalently,we consider the conditions on|z|1 under which p(z)0.Here we consider RK methods with nonsingularR.

Under the conditions already given,T11=(A⊗Is+hB⊗R)z is nonsingularwhenh is small.Ris nonsingular,so the pencil(A,B)is regular.Therefore T11=A⊗(Is+hB⊗R)z is nonsingular.So we have

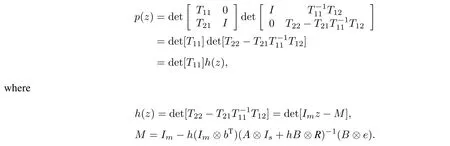
The matrix M does not depend on z and from the expression of h(z),it is clear that the zeros of h(z)are eigenvalues of M.So we just prove the eigenvalues of M are inside the unit circle.Since

Recall that the stability function of the RK method defined byR,bTis given by

Thus it adds no extra requirement on our RK method for stability.

(II) Applying(7)to block system 2,similar to that in(I),we get difference system(8)and

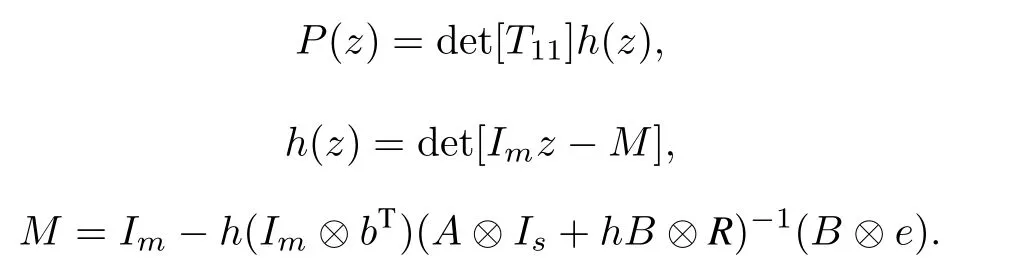
It is also true that the matrix M does not depend on z and from the expression of h(z),we see that the zeros of h(z)are eigenvalues of M.So we just prove the eigenvalues of M are inside the unit circle.Since

In this case,

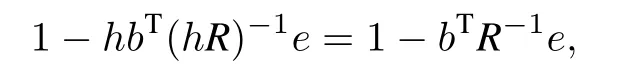
which requires the RK methods to satisfy

This is the requirement for RK methods to be strict stable.

(III) For block system 3,as pointed out in section 3,we investigate(4)in two cases: µ=0 and µ0.

(i) µ=0.It can be seen equation(4)has the same structure as block system 2.Therefore,we have the same P(z),h(z)and M as those in(II),which requires the RK methods to satisfy(11).

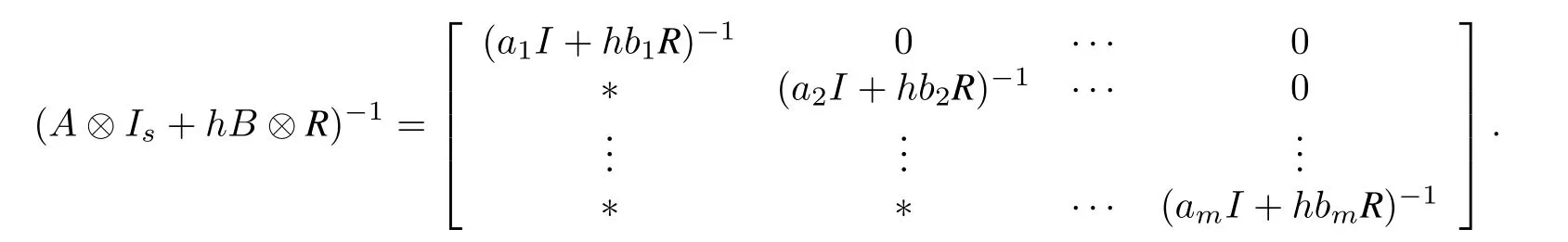
By the definition of the Kronecker tensor,we arrive at M in the following:

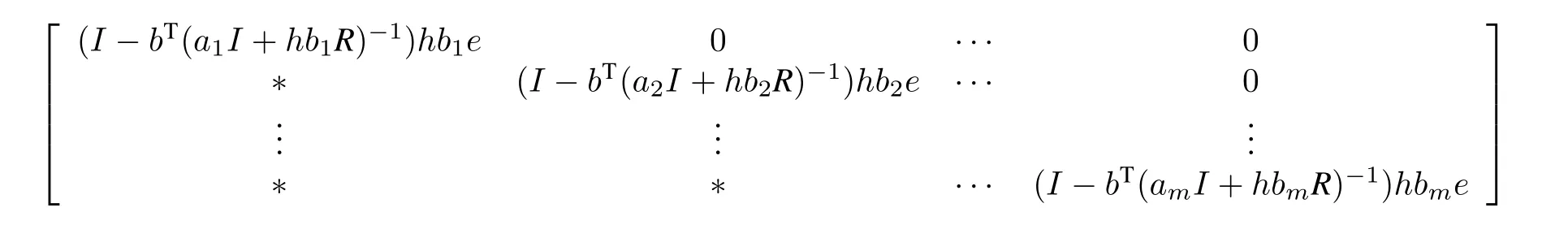
The stability function of RK method defined byRand bTis given by(10).As the second case(ii)of(III)in section 3,is just the singular value of the matrix pencil of(4)and as pointed out before,if the DAE is asymptotically stable,it will have nonzero negative real part.In this case,if hσ∈SR,where SRis the stability region of the RK method with coefficient matricesRand bT,we have This adds no extra requirement on our RK method for stability.

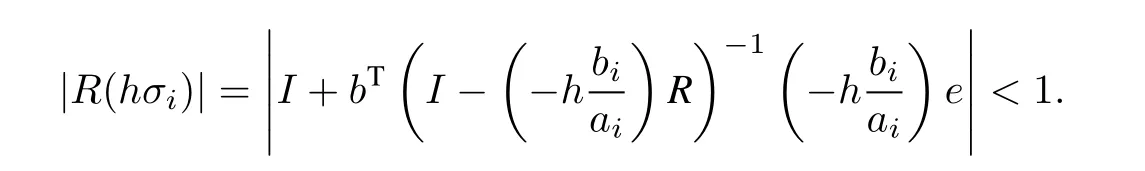
(IV) For block system 4,we apply(7)to(6).It can be seen that all the results concerning two cases µ=0 and µ0 are almost the same as in(III)exceptthat dimension of block system 4 is m×(m+1)instead of(m+1)×m.So the power of characteristic polynomial p(z)is m+s+1,while p(z)for block system 3 has power of m+s.Thus our RK method is stable.

Therefore we have shown the asymptotic stability of RK method for(1).

Theorem 8The RK method(7)withRnonsingular for the asymptotically stable system(1)is asymptotically stable if it satisfies the strict stability condition(11)and if hσiis in the stability region of(7)for all i,where σiare the singular values of the matrix pencil