The existence analysis of solutions for initial value problems of nonlinear conformable fractional delayed differential equations
2021-07-21WANGSenJIANGWei
WANG Sen,JIANG Wei
(School of Mathematical Sciences,Anhui University,Hefei 230601,Anhui,China)
Abstract:In this paper,we establish several existence and uniqueness results of solutions for initial value problems of nonlinear fractional delayed differential equations in the sense of conformable fractional derivative.The different results of existence of solutions are derived based on Banach fixed point theorem,Schauder fixed point theorem,successive approximations technique and the Gronwall inequality in the frame of conformable fractional integral,respectively.
Key words:existence and uniqueness;fixed point theorems;successive approximations technique;Gronwall inequality;conformable fractional calculus
1 Introduction
Fractional calculus[1−2]is a quite important branch of mathematical area and has been posed almost at the same time with the classical ones.There are several kinds of fractional operators that have been proposed so far,among which the well-known Gr¨unwald-Letnikov,Riemann-Liouville,Caputo definitions,the newly defined by ATANGANA et al[3]and CAPUTO et al[4],Caputo-Hadamard[5−6]derivatives,and so on.The unique property that these fractional calculi have in common may be the linearity,while not all these fractional derivatives obey the usual properties like the product rule,the chain rule,the Leibniz rule,etc.In order to overcome these or other difficulties,in 2014,KHALIL et al[7]first introduced a new simple and well-behaved fractional derivative called conformable fractional derivative.It is defined just on the basic limit definition and satisfies almost all the classical properties that the first-order derivative holds.In 2015,ABDELJAWAD[8]developed this new derivative further,he proposed many useful and valuable results about conformable fractional calculus.Since then,there have been more and more attentions[9−12]paid on this new derivative,and many questions were solved by using this definition.Particularly,in 2019,KHALIL et al[13]introduced the geometric meaning of conformable derivative via fractional cords.These works,to a large extent,strengthened our interest in proceeding on its study.
LI et al[14]studied the existence of solutions and Ulam’s stability for the following conformable fractional differential equations with constant coefficients

where λ is a nonzero real number andx(t)denotes the conformable fractional derivative(CFD)of x(t)starting from a of order α(which is given in definition 1)and f∈C([a,b]×R,R).
By introducing the notion of tube solution,BAYOUR et al[15]considered the existence of solution of the following local conformable fractional nonlinear differential equation

SOUAHI et al[16]investigated the stability and asymptotic stability of the following conformable fractionalorder nonlinear systems by using Lyapunov function

In[17],the finite-time stability problem(FTSP)and finite-time boundedness problem(FTBP)of conformable fractional order linear systems were discussed via Lyapunov method and linear matrix inequalities(LMI).
However,based on the above discussions and our range of knowledge,we find that no one has considereddelay in the existence of solutions for conformable fractional differential equations,while delay is indispensable both in mathematical model and natural phenomena due to its memory effect in many practical systems.With this as the motivation,in this paper,we first consider a general class of nonlinear fractional functional differential equations(FFDEs)in the sense of CFD
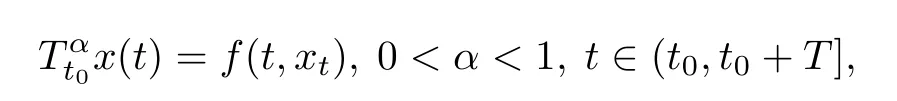
with the initial condition
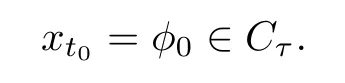
Here t0is the initial time,T is a positive real number,Cτ=C([−τ,0],R)denotes the space of continuously functions mapping the interval[−τ,0]into R,τ is a constant time delay and assumed that 0<τ Then,by selecting the operator f(t,φ)=Aφ(0)+Bφ(−τ)+f(t,φ(0),φ(−τ)),we further consider the existence and uniqueness of solutions of the following nonlinear fractional differential-difference equation in the frame of CFD where A,B are constant matrices,f(t,x(t),x(t−τ))∈C([t0,t0+T]×Rn×Rn,Rn). This paper is organized as follows.In section 2,some basic definitions and useful lemmas are introduced.In section 3,by applying fixed point theorems,we establish the existence and uniqueness results of the solution to(1).The main purpose of section 4 is to build an existence and uniqueness result of solutions to(2).An illustrative example will be given in section 5 to verify our results. This section collects some basic definitions and necessary lemmas. Definition 1[4]Let f:[a,+∞)→R be a function.Then the CFD starting from a of f of order α,0<α1,is defined by Lemma 1[4]Let α∈(0,1].If f is differentiable,then the following relationship between the CFD and the classical first-order derivative holds Definition 2[4]Let f:[a,+∞)→R be a function.Then the conformable fractional integral(CFI)starting from a of f of order α,0<α1,is defined by provided that the Riemann improper integral exists. Lemma 2[4]Let α∈(0,1]and f be a continuous function on[a,+∞).Then for all t>a,we have Further,if f is differentiable,then Definition 3[4−5]For every ta,the conformable fractional exponential function(CFEF)is defined by Lemma 3[4](conformable gronwall integral inequality)Let r(t)be a continuous,nonnegative function on[a,b)(for some b+∞)and let ξ,η be two nonnegative constants such that on this interval.Then the following inequality holds Lemma 4[20](Banach fixed point theorem)Assume that D is a non-empty closed subset in Banach space E and T:D→D is a contraction,that is,for any x,y∈D Then there exists a unique z∈D such that Tz=z,that is,T has a unique fixed point z in D. Lemma 5[20](Schauder fixed point theorem)Assume that K is a bounded,closed and convex set in Banach space E and P:K→K is completely continuous.Then there exists z∈K such that Pz=z,that is,P has a fixed point in K. This section is devoted to the establishment of existence and uniqueness results about the solutions of(1).Our approaches are based upon the fixed point theorems and successive approximations technique.We first give the concept of a solution of(1). Definition 4A function x is said to be the solution of(1),if x satisfiesx(t)=f(t,xt),t∈(t0,t0+T]and Remark 1According to lemma 2,under the assumption that the function x is differentiable on(t0,t0+T],it holds that and hence,(1)becomes This implies that the FFDE(1)is translated into an integer-order delay differential equation with variable coefficient(3),in which the state delay is contained in the nonlinear part of the equation.Thus it is difficult to study and find the existence results of the solutions.Therefore,as the method used in the cases of classical FFDEs described by Riemann-Liouville or Caputo derivative,we first apply the lemma 2 to transfer(1)into the following equivalent integral equation Thus,every solution of(4)is also a solution of(1)and vice versa. Let ρ be a given positive constant.Define the set Cρ={φ∈Cτ:ρ}.Before giving the main results,we propose the following hypotheses in this section. (H1):f(t,φ0)∈C([t0,t0+T]×Cτ,R). (H2):There exists a positive continuous function β(t)such that (H3):There exists a positive constant λ such thatβ(t)λ<1. (H4):f(t,φ0)∈C([t0,t0+T]×Cρ,R). (H5):There exists a positive constant L such that Firstly,we utilize the Banach fixed point theorem to establish the following theorem of existence and uniqueness of solutions for IVP (1). Theorem 1Supposethat(H1),(H2)and(H3)are satisfied.Then,there exists a uniquesolution for the IVP(1)on the interval[t0−τ,t0+T]. ProofWe define an operator M:C([t0−τ,t0+T],R)→C([t0−τ,t0+T],R)as Furthermore,we define the function y(·):[t0−τ,t0+T]→R as which implies xt=yt+ztfor every t∈[t0,t0+T],then the function z(·)satisfies with the zero initial condition In order to apply the Banach fixed point theorem,we define the set C0as with the norm Then C0is a Banach space.We further define another operator N:C0→C0as Note that the fixed points of N in C0coincide with the solutions of(5)in C0.Therefore,to prove that N has a fixed point in C0is equivalent to proving that M has a fixed point in C([t0−τ,t0+T],R).According to Banach fixed point theorem,as long as we prove that the operator N is contractive,then the existence of a fixed point of N in C0can be obtained.For any z,z∈C0and t∈[t0,t0+T],we have Next,another existence result will be derived by applying Schauder fixed point theorem. Theorem 2Suppose that(H4)holds.Then there exists a real number t1∈[t0,t0+T]such that the IVP(1)has at least one solution on the interval[t0−τ,t1]. Then C1is a Banach space,and apparently,C1is a closed,bounded,and convexset.For any element z∈C1,define an operator Q on C1as follows Now,we utilize Schauder fixed point theorem and divide it into three steps to prove the existence of a fixed point of Q in C1. Step 1 We show that Q:C1→C1is well defined.For any z∈C1,from the continuity and boundedness of f(s,ys+zs),it can be deduced that(Qz)(t)is continuous on[t0,t1]and for all t∈[t0,t1].This implies that Q(C1)⊂C1,and hence Q:C1→C1is well defined. Step 2 We prove that Q is continuous.Let{z(n)}be a sequence with z(n)→z in C1.For each t∈[t0,t1],we have which tends to zero as δ→0.Therefore,Q(C1)is equicontinuous.In addition,clearly,Q(C1)is uniformly bounded.Accordingto Arzela-Ascoli theorem,we know Q(C1)is relatively compact.Schauder fixed point theorem guarantees that Q has a fixed point in C1. Finally,the successive approximations technique will be adopted to derive an existence and uniqueness result of solutions for(1). Following(H4)and(7),it is easy to verify that the above sequence is well-defined.Now,we divide this proof into four steps. Step 1 For all t∈[t0−τ,t0+h]and n∈N+,we apply mathematical induction to prove that In fact,for all t∈[t0−τ,t0],in view of(6)and(7),we know that|x(n)(t)−x(0)(t)|=0ρ,and hence,(8)holds.Therefore,we only need to prove that(8)holds for all t∈[t0,t0+h]. (i)For n=1 and t∈[t0,t0+h], which implies that step 1 is completed. Step 2 We show that x(n)(t)is uniformly convergent on[t0,t0+h].Consider Following the procedure in step 2,it yields that x(n)(t)is uniformly convergentto y(t)on[t0,t0+h]when n→∞.This indicates that x(t)≡y(t)holds for t∈[t0−τ,t0+h].This completes the proof. Remark 2The technique of successive approximations utilized in the proof actually provides us a method to obtain the estimates of the solutions.That is to say,if we take x(t)=y(t)in(11),we can get the following error estimates for the nth approximation x(n)(t)and the true solution x(t)within the interval[t0,t0+h] In this section,the existence and uniqueness of solutions of a class of nonlinear fractional differential-differenceequation in the frame of CFD will be investigated via conformable Gronwall integral inequality presented in lemma 3.Let|x|(·)be any vector norm(e.g.,·=1,2,∞)anddenotes the matrix norm induced by this vector.Here we consider the following assumption. (A1):There exists a positive constant β such that Theorem 4Suppose that(A1)is satisfied.Then(2)has a unique solution. ProofFirstly,we know that x∈C([t0−τ,t0+T],Rn)∩C1([t0,t0+T],Rn)is a solution to(2)if and only if Secondly,let x(t)and y(t)be any two solutions of(2).Then x(t)and y(t)both satisfy(13).If we set z(t)=x(t)−y(t),then one can easily get z(t)=0 for t∈[t0−τ,t0].While for t∈[t0,t0+T], When θ∈[t0,t0+τ],it can be deduced that z(θ−τ)=0,hence That is to say,z(t)=x(t)−y(t)=0,namely,x(t)=y(t)holds for all t∈[t0,t0+τ].When t∈[t0+τ,t0+T],we further have Applying the appropriate property of the norm,yields that Therefore,z(t)=x(t)−y(t)=0,namely,x(t)=y(t)also holds for all t∈[t0+τ,t0+T].In conclusion,x(t)≡y(t)holds for all t∈[t0−τ,t0+T],this implies the uniqueness. In this section,an example will be given to illustrate our results. Example 1Consider the following FFDE in the frame of conformable derivative with the initial conditon
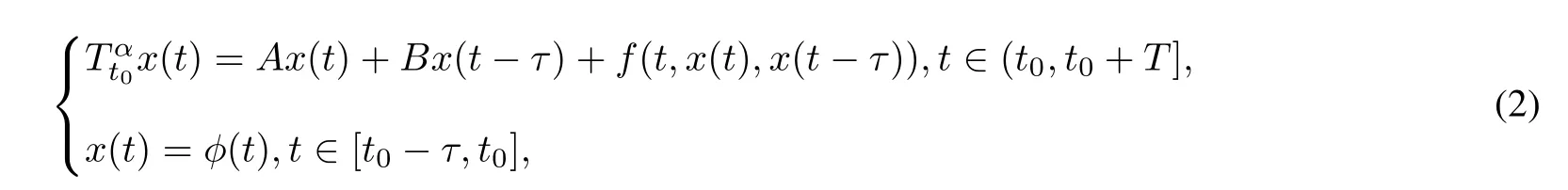
2 Preliminaries




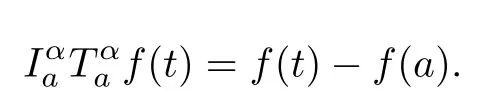
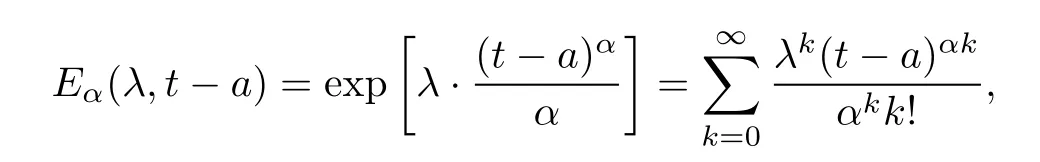
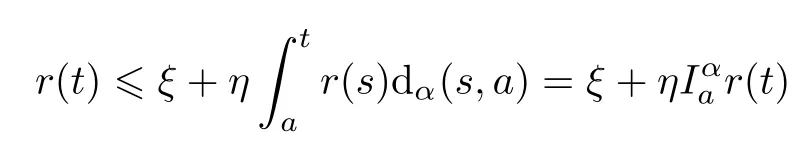


3 Existence of solutions for(1)

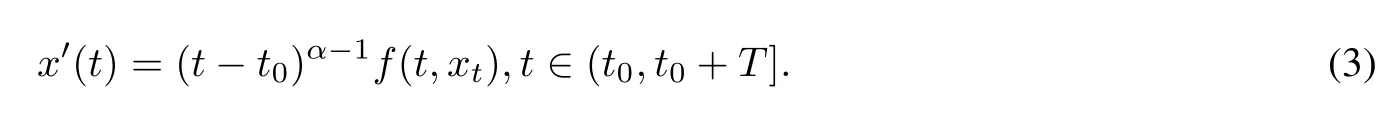



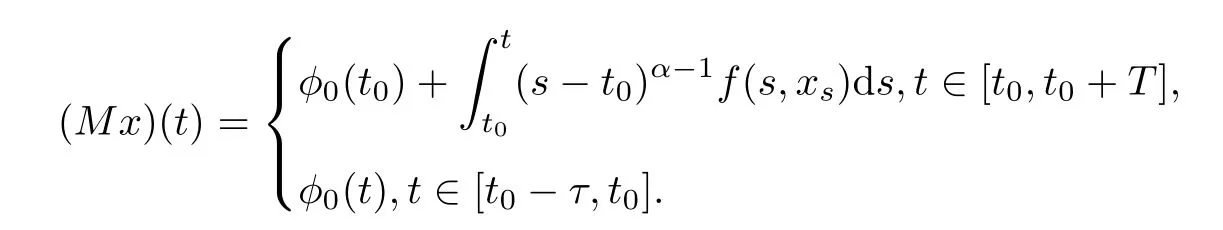
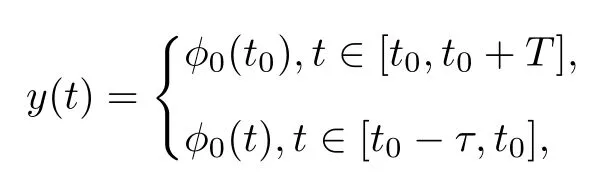


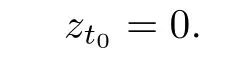




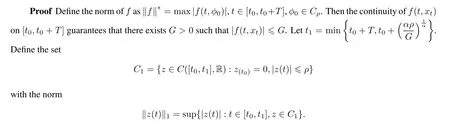
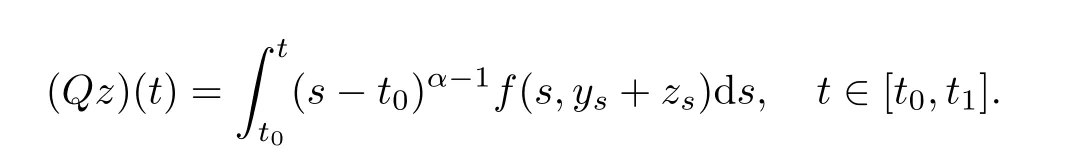




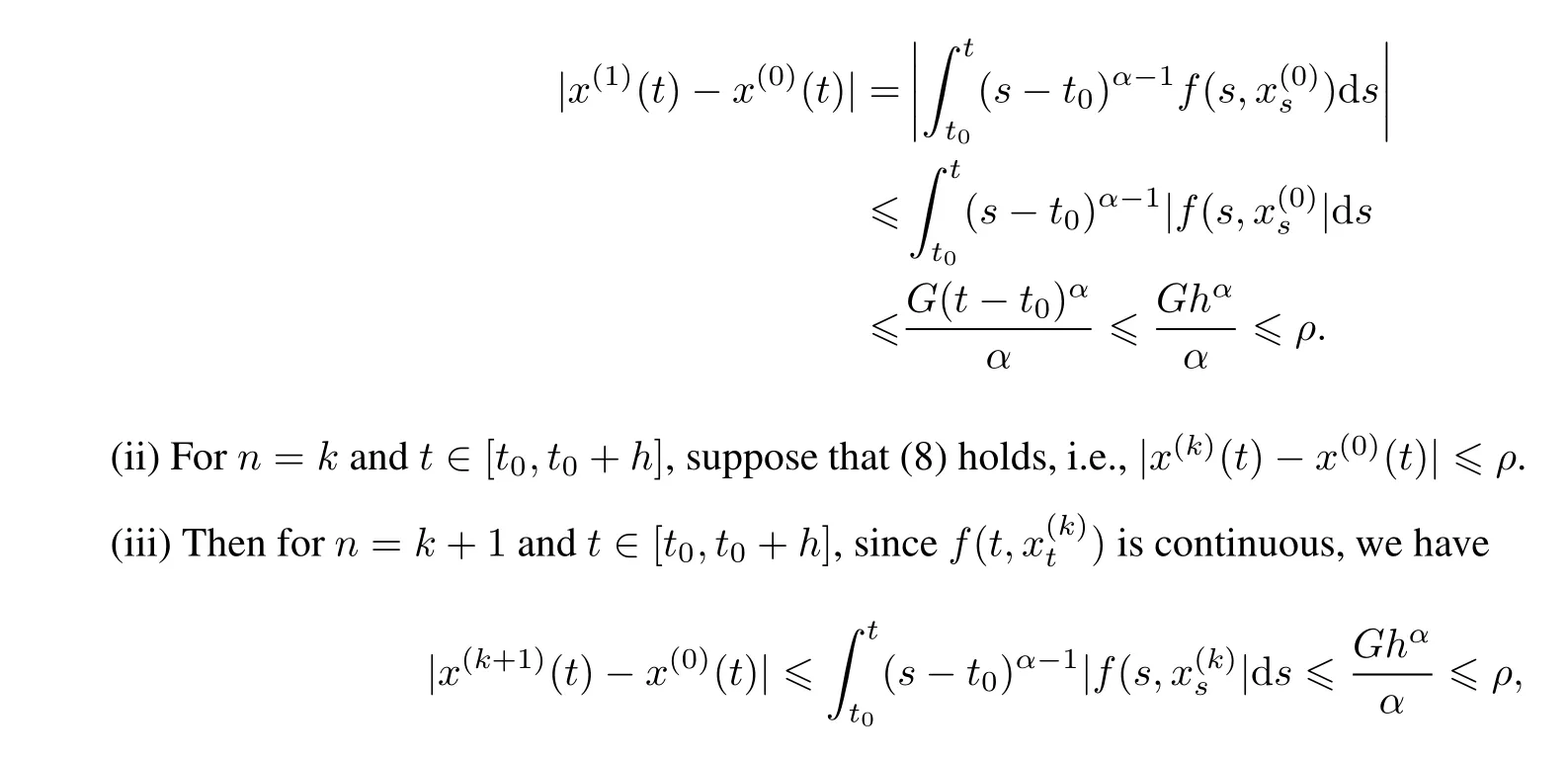



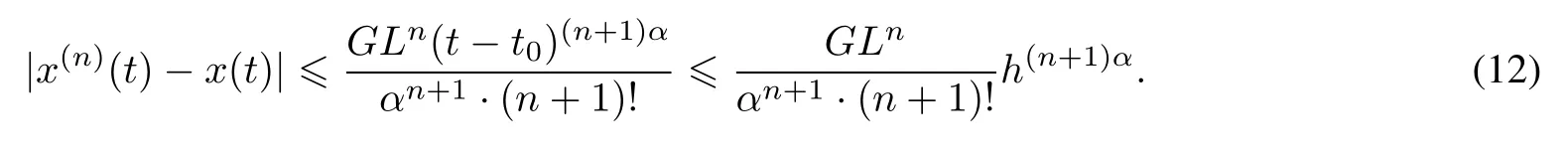
4 Existence and uniqueness of solutions for(2)
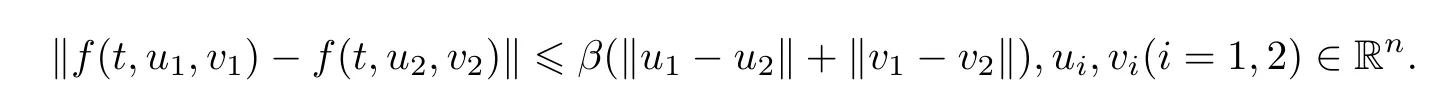
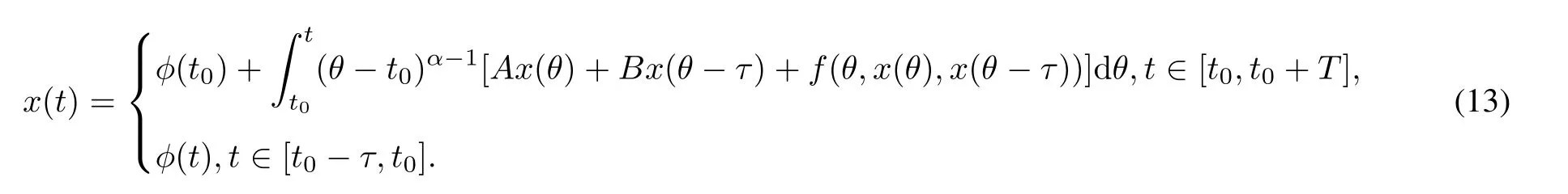
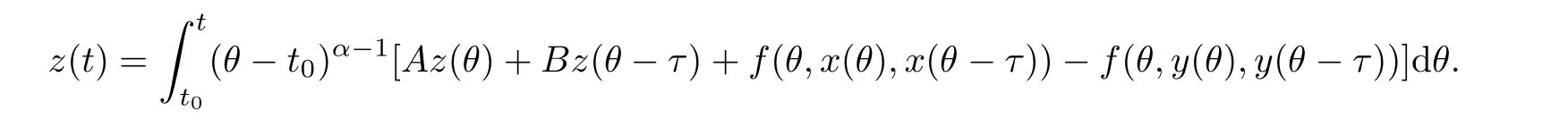
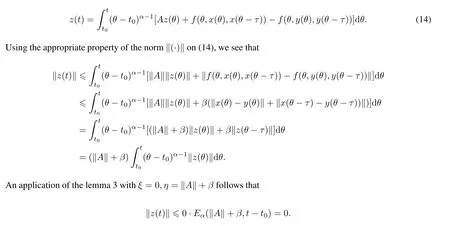
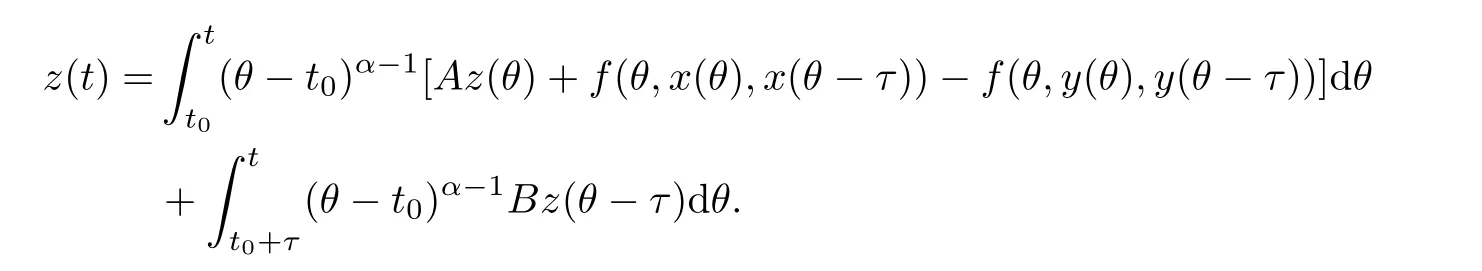

5 An illustrative example


杂志排行
上海师范大学学报·自然科学版的其它文章
- Multiple rogue wave and multiple lump solutions of a(3+1)-dimensional Korteweg-de Vries equation
- Asymptotic stability of linear multistep methods and Runge-Kutta methods for homogeneous differential-algebraic equations with rectangular coefficients
- A spectral method for Burgers equation using Jacobi polynomial
- A graph-theoretic approach to topology identification of stochastic multi-group models with multiple dispersal
- Reflection ordering in the imprimitive complex reflection group G(m,p,n)
- Anti-periodic solution for fuzzy differential equations
