Invariant algebraic surfaces of a chronic wasting disease model

YANG Yang,XIE Feng

(College of Science,Donghua University,Shanghai 201620,China)

Abstract:In this paperwe study a chronicwasting disease(CWD)model of three dimensional ordinary differential equations.We use the method of characteristic curves to give a complete classification of this system with invariant algebraic surfaces.In addition,we give some conditions of this system on the existence of generalized first integrals.

Key words:chronic wasting disease(CWD)model;invariant algebraic surfaces;Darboux polynomials

1 Introduction

In this paper,we consider the three dimensional chronic wasting disease(CWD)model:

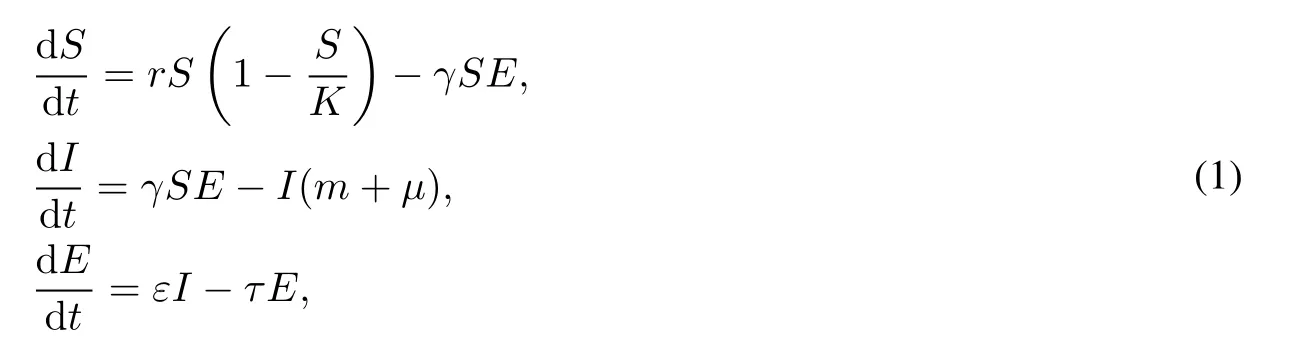
which is proposed by SHARP and PASTOR[1].Here S is the number of susceptible animals,I is the number of infected animals,and E is the mass of prions per km2.The parameters have the following meaning interpretation:r is the net per capita growth;K is the carrying capacity number of individuals per 100 km2;γ is the possibility of transmission via random encounter from the environment to susceptible animals;m is the mortalitywith non-disease; µis the chronic wasting disease related mortality rate;ε is the prions excrete rate from infected animals to the soil;τ is the loss rate of active prions in the soil.This model is based on a model of chronic wasting disease in mule deer:

which was developed by MILLER et al[2−4].The parameter a is the quantity of births per unit of time,and is assumed to be a constant in this model,and the other variables and parameters are the same as those in system(1).However,this constant assumption is not well applied to wildlife populationsince it takes two years instead of one or two decades to give birth as human beings do.Therefore,model(2)was modified by ANGELA SHARP and JOHN PASTOR;they replaced the constant birth rate a with a logistic growth term and removed m from the first equation of model(2)since density dependent mortality is subsumed into the logistic growth term.

For a better understanding we rewrite all the variables and parameters in familiar.We set x=S,y=I,z=E,α=r,β=γ,K=b,and get

This paper studies the invariant algebraic surfaces of the system(3)since it connects the algebraic geometry and the construction of first integral from the perspective of integrability.The search of first integrals and invariant algebraic surfaces is important in the study of integrability[5−8].

Now we recall some definitions that will be used in this paper.

Let f(x,y,z)be a real polynomial in the variables x,y and z.If there exists a polynomial k(x,y,z)such that

then f(x,y,z)is called a Darboux polynomials of the system(3),and k(x,y,z)is called the cofactor of f(x,y,z).From equation(4)we know that if an orbit of system(3)has a point on an invariant algebraic surface then the whole orbit is contained in this surface.So we call that f(x,y,z)=0 is an invariant algebraic surface of the system(3).It is easy to prove that the degree of k(x,y,z)is less than or equal to 1.Without loss of generality,we can write the cofactor in the form:

The Darboux polynomial is called a first integral of the system(3)when k(x,y,z)=0.In particular,if a first integral H(x,y,z,t)is a polynominal and independent of t,then it is called a polynomial first integral;it is called a rational first integral when it is a rational function independent of t.System(3)is completely integrable if there are two independent first integrals.

Here we give an important proposition that gives the relation between different Darboux polynomials and their cofactors.Proof can be found in[9]and[10].

Proposition 1Assume that f(x,y,z)is a polynomial function and it has an irreducible decomposition f=,then f is a Darboux polynomial with cofactorif and only if each fiis a Darboux polynomial with cofactorfor i=1,2,···,m.

The next proposition is also necessary for our proof of main results,see[11].

Proposition 2Assume that system(3)has a singular point p,and λ1,λ2,λ3are the eigenvalues of the linear part of the system at p.Then the number of functional lyindependent generalized rational first integrals of system(3)is at most the dimension of the minimal vector subspace of R3containing the set

We note that when β=0,the dynamics of system(3)are simple and so omitted.

2 Main results

In this section we give our main results.

First we provide some generalized first integrals under particular conditions on parameters.

Theorem 1When β0,ε=0 and τ0,system(3)has a first integral

Theorem 2When βε0 and α=0,system(3)has an analytic first integral

In addition,system(3)is completely integrable with another generalized rational first integral if τ=m+ µ,and the second generalized rational first integral

Besides,system(3)is not completely integrable with generalized rational first integrals if τ(m+ µ).

Proposition 3If f(x,y,z)is a Darboux polynomial of system(3),then cofactor k(x,y,z)is of the form k=px+rz+c.The homogeneous component of the highest degree of f(x,y,z)is of the form

Theorem 3System(3)has irreducible Darboux polynomials if and only if one of the following three cases holds:

(a)there exists a Darboux polynomial f(x,y,z)=x with cofactor k=−−βz+α;

From theorem 3 we can obtain the following results.

Theorem 4When βεα0,system(3)has no rational first integral.

In theorem 3 we use the method of characteristic curves to find all the Darboux polynomials of system(3)and give the corresponding parameter conditions.Firstly we give a proposition 3 which is fundamental for the proof of theorem 3.

Corollary 1When ε=0,system(3)has a unique irreducible invariant

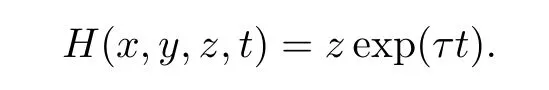
In the next section we will give the proofs of the results above.

3 Proofs of the main results

3.1 Proof of theorem 1

We consider system(3)with ε=0,β0 and τ0,which is

From system(6)we have

which means that if H(x,y,z)is a constant on each plane,then

It is easy to check that H(x,y,z)is a first integral.

3.2 Proof of theorem 2

If α=0,system(3)turns into

It is easy to check that H1and H2are two generalized rational first integrals.So we only need to prove that there is no other generalized first integral except H1when τm+ µ.

Obviously,the left side of equation(8)is a rational number since k2,k3∈Z,the right side of equation(8)is irrational when x is chosen suitably.Thus equation(8)cannot hold for this choice of x.Therefore,for those singular points(x,0,0),there is clearly at most one dimension for the minimal vector subspace of R3containing the set

generated by(k1,0,0).Thus,system(7)can only have one generalized rational first integral H1.

3.3 Proof of proposition 3

Substituting f(x,y,z)and k(x,y,z)into equation(4),we have the homogeneous items of degree n+1:

Now we use the method of characteristic curves to solve equation(9).The characteristic equations associated with equation(9)are

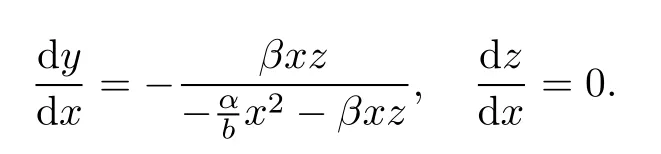
Their general solutions are

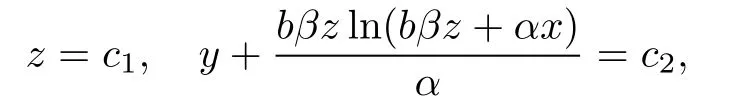
where c1and c2are arbitrary constants.

By taking a transformation of variables:

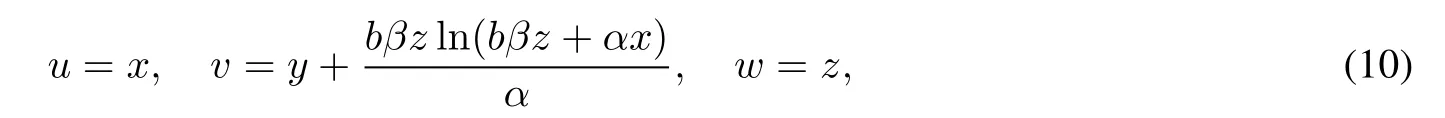
and the inverse transformation:

we get an ordinary differential equation:

from equation(9).

Solving equation(12),we get

where Fnis an arbitrary function of v and w.

Then we have explicit solution of equation(9)

Since fnis a homogeneous polynomial of degree n,we must have q=0.Then

and k(x,y,z)=px+rz+c.It completes the proof of proposition 3.

3.4 Proof of theorem 3

4 Conclusion

In this paper,we classify all the Darboux polynomials of CWD system,and prove that there is no rational first integral when βεα=0.In addition,we give some conditions when CWD system has generalized first integrals.It is completely integrable when βε0,α=0 and τ=m+ µ.