Generalization of existence theorems of root and its application
2021-07-21CHENHuiqinZHAOXianglanCHENFuFENGWenying
CHEN Huiqin ,ZHAO Xianglan ,CHEN Fu ,FENG Wenying
(1.School of Mathematics and Statistics,Shanxi Datong University,Datong 037009,Shanxi,China;2.Department of Mathematics,Trent University,Peterborough K9J 0G2,ON,Canada)
Abstract:It is well known that the existence of roots theorem for continuous functions not only is important in Mathematical Analysis,but also has wide applications.In this paper,we generalize the existing theorems in this area to compounded functions.Application of the obtained results is also shown by examples.
Key words:continuous function;zero point;existence theorem of root
1 Introduction
In[1],the existence theorem of roots is a special case of the intermediate value theorem.However,many problems about the intermediate value theorem are solved by the application of some existence theorem of roots.In addition,the zero of a function f(x)is essentially the root of the equation f(x)=0 by its definition.So,a theorem about the existence of roots is actually a theorem for zero point.
Existence theorems of roots and intermediate value theorems are also widely used in solving inequalities,theoretical analysis and some practical application problems.They are especially important in discussing whether the solution of an equation exists.Existence theorems of roots can be used to discuss the existence of solutions,positive solutions and the range of solutions for both algebraic and differential equations.Existence theorems of roots certainly also play a very important role in practical applications.Therefore,they have attracted great attention of mathematicians and a great amount of research have been done in this area.The differences between the work of different researchers are the direction of generalization and how they are generalized.As stated by the author of[2–7],some scholars start with closed intervals and generalize it to arbitrary intervals,some scholars start with the value of a function being finite at the endpoint of the interval and generalize it to the case that the value can be infinite,and other scholars extend the intermediate value theorem to the case of the discontinuous functions by releasing the traditional condition that the function must be continuous.
This paper is influenced by[8],and we improve the existing theorems of roots and extend them to composite functions.This not only promotes the theoretical development of mathematical analysis and advances mathematics,but also provides a different method for determining the solutions of equations.
We first give the definition of zero point of a function and the basic theorem for the existence of root.
Definition 1Let f(x)be a function defined on[a,b].A point ξ∈[a,b]is called a zero point of f(x)on[a,b]if f(ξ)=0.
Lemma 1[1]Suppose that f(x)is a continuous function on the interval[a,b],and f(a)f(b)<0.Then there exists at least one point ξ∈(a,b)such that f(ξ)=0.
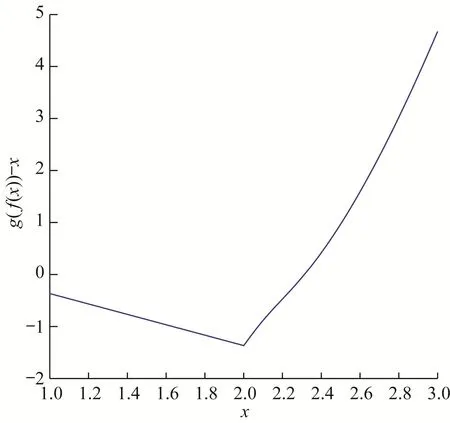
Lemma 2[1]Suppose that f(x)is a continuous function on the interval[a,b],and f(a) Lemma 2 can be easily obtained by applying lemma 1 to the auxiliary function F(x)=f(x)−x.Lemma 1 and lemma 2 are called existence theorems of roots,also known as zero point theorems. The intervals in lemma 1 and lemma 2 are finite closed intervals.We first generalize the intervals of these two lemmas to any interval.We will work on the interval(a,b)where a and b can be finite or infinite.Other intervals are similar. Theorem 1Suppose that f(x)is a continuous function on the interval(a,b).If f(a+0)=and f(b−0)=exist,and f(a+0)f(b−0)<0.Then there exists at least one point ξ∈(a,b)such that f(ξ)=0. ProofWe consider the case with f(a+0)<0,f(b−0)>0.The other case is very similar.By the definition of limit,there exist points x1∈(a)and x2∈(b)(x1 Since the function f(x)is continuous on[x1,x2],by lemma 1,there exists at least one point ξ∈(x1,x2)⊂(a,b)such that f(ξ)=0.The proof is completed. The interval(a,b)of theorem1 is all the intervals,so we have extendedlemma 1 and lemma 2 from the original fi nite closed interval to any interval.In addition,the original condition of opposite signs of the function values at the endpoints of the interval is changed to opposite signs of the limit values at both ends of the interval.Of course,the one side limit at the end of these intervals can be finite or+∞or−∞(see[2]). Theorem 2Suppose that f(x)is a continuous function on the interval(a,b),f(a+0)=f(x)and f(b−0)=f(x)exist and are fi nite,and one of the following conditions is satis fi ed: (i)f(a+0) (ii)f(a+0)>a,f(b−0) ProofWe will prove case(i)only since case(ii)is very similar.Let Then F(x)is continuous function on the interval[a,b].Consequently By lemma 2,there is at least one point ξ∈(a,b)such that F(ξ)=ξ,that is f(ξ)=ξ. The main theorems of this paper establish a few zero point theorems on composite functions. Theorem 3Suppose that f(x)is a continuous function on the interval[a,b].If c is a real number such that f(ca)a and f(cb)b(or f(ca)a and f(cb)b)are true,then there exists at least one point ξ∈[a,b]such that f(cξ)=ξ. ProofLet F(x)=f(cx)−x,then the function F(x)is continuous on the interval[a,b].As If F(a)=0 or F(b)=0 is true,then we can take ξ=a or ξ=b. If F(a)F(b)<0 is true,by lemma 1,there exists at least one point ξ∈(a,b)such that F(ξ)=0.That is f(cξ)=ξ.The proof is completed. Theorem 4Let g(x)be a continuous functionon the interval(0,+∞),andf(x)be a nonnegative continuous function on the interval[a,b].Suppose that there exist two positive numbers m and M,such that and one of the following conditions is satisfied: Then there exists at least one point ξ∈[a,b]such that g(f(ξ))−ξ=0.That is,equation g(f(x))=x has at least one solution on[a,b]. ProofWe prove the theorem for case(i)only since the proof for case(ii)is very similar.By the conditions,we know that the composed function g(f(x))is continuous on[a,b].As If g(f(a))=a or g(f(b))=b is true,then we can take ξ=a or ξ=b. Theorem 5Let g(x)be a continuous functionon the interval(0,+∞)and f(x)be a nonnegative continuousfunction on the interval(a,b).Suppose that both f(a+0)=and f(b−0)=exist,and there exist two positive numbers m and M,such that and one of the following conditions is satisfied: Then there is at least one point ξ∈(a,b)such that g(f(ξ))−ξ=0.That is,equation g(f(x))=x has at least one solution on(a,b). ProofWithout loss of generosity,we assume that condition(i)is true.Set Then ϕ is a continuous function on the interval[a,b].Consequently By theorem4,thereis at least onepointξ∈[a,b]suchthat g(ϕ(ξ))=ξ.Namely,thereis at least onepoint ξ∈(a,b)such that g(f(ξ))=ξ. The main results of this paper are theorem 4 and theorem5.They provide a new method for determining whethercomposition of two functions has a zero point.The advantage of these theorems over the traditional methods(lemma 1 and lemma 2)is that one can analyze two simple functions instead of one complicated function for zero solutions.The existence of zero point of a compound function is determined by the properties of the outer function g and the inner function f.In the case that g and f are easier to analyze or their composition g◦f cannot be easily found,it is convenient to use theorem 4 or theorem 5. In this section,we give several concrete examples to show applications of the results obtained in section 2. where m=1,M=2.f(x)is a nonnegative continuous function on the interval[1,3],and Thus g and f satisfy the conditions of theorem 4.Therefore,the equation g(f(x))=x has roots over the interval[1,3].The plot of the function g(f(x))−x is shown in figure 1.It is clear that the equation g(f(x))=x has a root over the interval. Figure 1 The graph of the function g(f(x))−x on the interval[1,3] Competing interestsThe authors declare that they have no competing interests. AcknowledgementsThe authors are very grateful to the reviewers for their valuable suggestions and useful comments,which led to an improvement of this paper.2 Main results
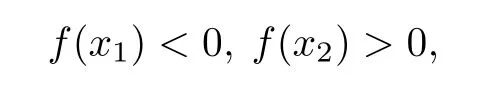
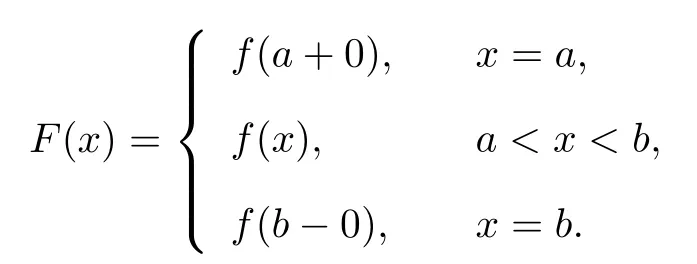
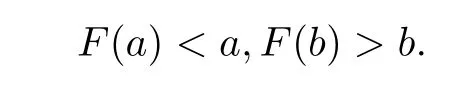
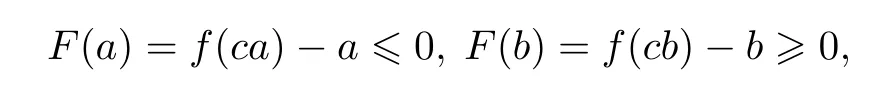
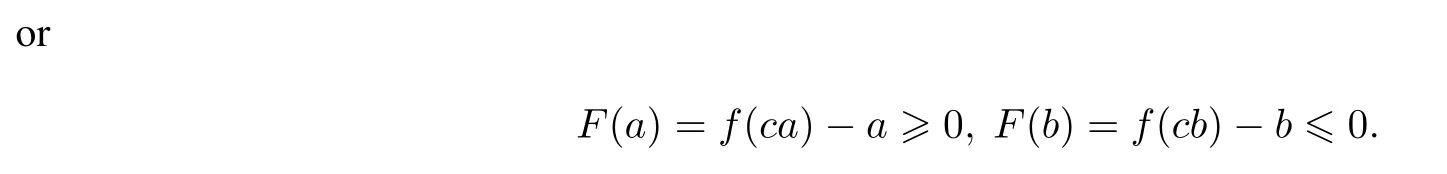
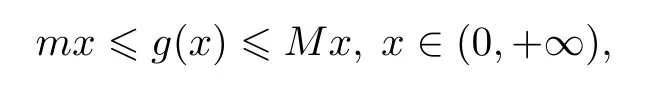

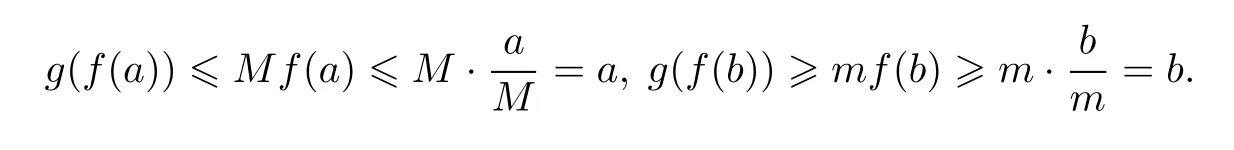
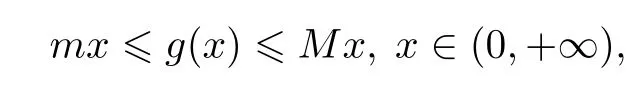

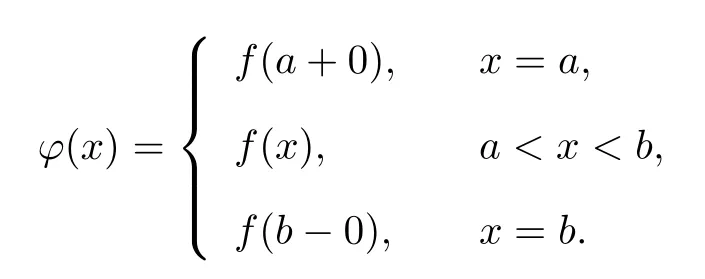

3 Some examples

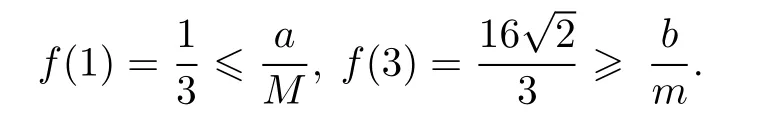
杂志排行
上海师范大学学报·自然科学版的其它文章
- Multiple rogue wave and multiple lump solutions of a(3+1)-dimensional Korteweg-de Vries equation
- Asymptotic stability of linear multistep methods and Runge-Kutta methods for homogeneous differential-algebraic equations with rectangular coefficients
- A spectral method for Burgers equation using Jacobi polynomial
- A graph-theoretic approach to topology identification of stochastic multi-group models with multiple dispersal
- Reflection ordering in the imprimitive complex reflection group G(m,p,n)
- Anti-periodic solution for fuzzy differential equations
