基于伪随机序列的压缩感知测量矩阵构造

杨俊坡，刘文远

(陕西科技大学 电子信息与人工智能学院, 陕西 西安 710021)

0 引言

2006年，压缩感知(Compressed sensing，CS)的相关理论首次由Donoho和Candès等[1,2]学者提出，以远低于信号频率的采样率完成稀疏信号的采样和重构，从而实现与Nyquist采样定理不同的全新采样算法.由于其信号采样率不再受Nyquist采样定理的限制，压缩感知的理论研究受到了学术界的广泛关注.一般而言，压缩感知算法的计算过程主要可分为数据采样和信号重构.在数据采样过程中，优秀的测量矩阵可将高维原始信号投影至低维空间，以较低的计算强度获取相同精度的数据；在信号重构过程中，优秀的测量矩阵以更高的概率精确地重构原始的稀疏信号.总之，测量矩阵直接决定了压缩感知算法的信号采样和重构质量.

随着压缩感知理论研究和应用技术的逐渐深入，很多学者做出了大量的研究[3-13].其中，Candes和Tao[14]在文献中提出了测量矩阵的约束等距性(Restricted Isometry Property，RIP)，结果表明，测量矩阵需要满足RIP性质，才可以以较高的概率精确地重构原始信号.根据这一结论，文献[4-6]分别基于LDPC(Low Density Parity Check)码、Berlekamp-Justesen码和Vandermonde矩阵提出了确定性测量矩阵的构造方法，极大地丰富了确定性测量矩阵的种类.然而，这些测量矩阵均存在硬件实现复杂的缺点，这导致压缩感知算法的实际应用受到较大的限制.

为了解决确定性测量矩阵硬件实现复杂的问题，文中从m序列的采样序列出发，引入了具有较低相关性的二进制伪随机序列，在此基础上，利用该序列的双极性矩阵构造确定性的测量矩阵.仿真实验表明，在同条件的压缩感知算法中，本文提出的测量矩阵的重构性能优于Gaussian随机矩阵.

1 预备知识

1.1 压缩感知

在压缩感知算法中，不妨用Φ表示M×N维的测量矩阵(M×N)，此外，X表示N维的原始信号，且该信号是k稀疏的，Y表示经过采样的M维观测信号.在信号采样过程中，原始信号、测量矩阵和观测信号之间存在线性的关系：

Y=ΦX

(1)

而在压缩感知算法中，信号的重构计算属于非线性的NP困难问题，即通过使用最小1范数优化方法，将观测信号Y重构成原始信号X，其计算过程如式(2)所示：

(2)

目前，应用最小1范数优化方法的具体算法主要包括基追踪(Basis Pursuit，BP)、贪婪追踪类和正交匹配追踪(Orthogonal Matching Pursuit，OMP)等算法.一般而言，OMP等追踪算法利用多轮迭代的方法得到局部最优解，尽量逼近全局最优解，从而最终获取原始信号的精确估计值.

定义1对于维度为M×N的测量矩阵Φ，不妨设φ0,φ1,…,φN-1表示Φ的列向量，即Φ=[φ0,φ1,…,φN-1]，则其测量矩阵Φ的相关性μ(Φ)定义如式(3)所示

(3)

其中，〈φi,φj〉表示列向量φi与φj之间的内积，‖φi‖表示第i+1个列向量的模长.

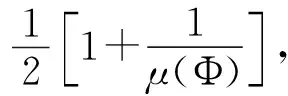
由引理1可知，如果降低测量矩阵的相关性，则可重构信号x′的稀疏度k可以增加.总之，在构造过程中，测量矩阵的相关性应该尽量降低，从而改善压缩感知算法的重构性能.

1.2 有限域

由于测量矩阵的构造需要使用伪随机序列，所以文中仍需要介绍一些有限域的基本知识.这里不妨使用Fp表示包含p个元素的有限域，其中p是素数，其本原元元素为α.n为正整数且q=pn，则Fq是有限域Fp的扩域，所含元素的表示为{0,1,…,q-1}.此外，Fq{0}是包含q-1个元素的乘法群，其群元素表示为{1,α1,α2,…,αpn-2}.

定义2设p为素数，n和m均为正整数，且m|n，x∈Fpn，则从域Fpn到其子域Fpm的迹函数公式为

(4)

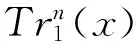
2 测量矩阵

为了构造具有优秀信号重构功能的确定性测量矩阵，基于传统的m序列，通过调整其采样系数，分别获取了奇数和偶数情况下的二进制伪随机序列，并且使用迹函数的方式，构造具有双极性特征的确定性测量矩阵.

2.1 矩阵构造

伪随机序列是具有随机特性的确定序列，一般由m序列经过采样或组合形成.其中，采样的m序列可以直接使用有限域中的迹函数进行表示，而迹函数中自变量的指数，即为伪随机序列的采样系数.利用这样的方法，文中分别引入奇数和偶数情况下的二进制伪随机序列，在此基础上，利用迹函数的结构，提出双极性测量矩阵的构造方法和相应公式.

定义3设l和ρ是正整数且ρ∈[1,l]，设定由有限域元素组成的矩阵Λ2nρ×ρ，令λi,j(0≤i≤2nρ-1,

0≤j≤ρ-1)表示第i+1行第j+1列的矩阵元素，这两者之间的关系如式(5)所示.

Λ2nρ×ρ={λi,j|λi,j∈F2n,0≤i≤2nρ-1,

0≤j≤ρ-1}

(5)

构造1设l和ρ是正整数，l≥2且1≤ρ≤l，则奇数n=2l+1,则可以构造大小为M×N(M=2n-1，N=2nρ)的压缩感知测量矩阵Φ，其具体公式如式(6)所示

Φ=[φ0,φ1,…,φ2nρ-1]

(6)

其中，φi(0≤i≤2nρ-1)是测量矩阵Φ的第i+1个分量，同时也是一个周期为2n-1的二进制采样m序列，如式(7)所示

φi=(si,0,si,1,…,si,2n-2)T

(7)

而φi的第j+1个分量si,j(0≤j≤2n-2)也是采样m序列的第j个变量，其计算如式(8-9)所示

si,j=(-1)fodd(i,j)

(8)

(9)

其中，α是有限域F2n中的本原元.

构造2与奇数情况类似，令l≥2,1≤ρ≤l和n=2l，大小为M×N(M=2n-1，N=2nρ)的压缩感知矩阵Φ为

Φ=[φ0,φ1,…,φ2nρ-1]

(10)

而其第i+1个分量如式(11)所示

φi=(si,0,si,1,…,si,2n-2)T

(11)

而φi的第j+1个分量si,j如式(12)所示

si,j=(-1)feven(i,j)

(12)

(13)

在构造1和2中，文中分别提出了奇数和偶数变元情况的双极性测量矩阵的构造方法.由于测量矩阵构造是在m采样序列的基础上构造的，所以其硬件和软件实现方式更加容易，即基于伪随机序列的测量矩阵具有优秀的实用性.

2.2 相关性

根据引理1可知，矩阵相关性是测量矩阵的重要衡量指标，降低其相关性，可以提高算法的信号重构性能.针对基于伪随机序列的测量矩阵构造，文中计算了测量矩阵的最大相关性，并从理论上与Gaussian随机矩阵进行了充分的对比和分析.

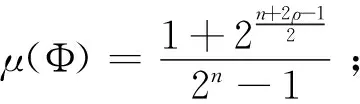
证明：由构造1可知，当n=2l+1或n=2l时，测量矩阵Φ均包含2nρ个列向量φi(i∈[0,2nρ-1])，而这些列向量的模长‖φi‖均为固定值，其计算公式如下所示

(14)

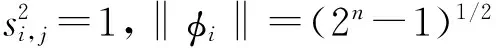
(15)

(1)当n=2l+1时，

(16)

其中，

g(i,j,z)=Tr((λi,0+λj,0)z)+

(17)

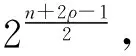
(18)

(2)当n=2l时,

(19)

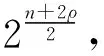
2.3 相关性比较

为了进一步衡量本文测量矩阵构造的具体性质，文中分析了Gaussian随机矩阵的相关性数值，并与构造1和2的测量矩阵进行了细致的比较.

引理2不妨设gi和hi是Gaussian随机矩阵Gp×q的任意两个列向量，这两个列向量是符合N(0,σ2)的独立同分布的高斯随机序列，则列向量之间相关性的概率分布满足式(20).

(20)

定理2在同样的条件下，对于构造1和2中(2n-1)×2nρ的测量矩阵Φ，其相关性μ(Φ)小于同样大小的Gaussian随机矩阵G.

(21)

f(n)是关于n的减函数，关于ρ的增函数，这表明，当ρ=1且n=5时，f(n)取得最大值，f(n)≤f(5)=6.77×10-4，此时，

(22)

当n是偶数时，经过推导可以得到与奇数情况下相同的结论，所以定理2得证.

3 仿真与分析

结合定理1和2的结果可知，从理论分析的角度出发，与Gaussian随机矩阵相比，基于伪随机序列的测量矩阵具有更低的相关性，这也意味着其重构性能更加优秀.为了进一步证明和验证测量矩阵的信号重构性能，通过对不同稀疏度的信号采样和仿真，文中实现了Gaussian随机矩阵和确定性测量矩阵的重构性能比较.

在仿真的矩阵构造阶段，对于确定性测量矩阵，令ρ=2，文中构造和实现偶数情况n=8和奇数情况n=7的矩阵，其测量矩阵大小分别为255×65 536和127×16 384；同样地，文中生成了大小为255×65 536和127×16 384的独立同分布Gaussian随机矩阵，用于仿真比较和分析.在仿真的信号重构阶段，文中选用了正交匹配追踪(OMP)算法，作为信号的重构算法.此外，需要说明的是，文中随机生成了不同稀疏度k的信号x，其维度分别为65 536×1和16 384×1，奇数情况n=7和偶数情况n=8下，测量矩阵信号重构性能仿真的具体情况和分析如下：

3.1 奇数测量矩阵仿真

当n=7时，信号稀疏度k设置在区间[10,40]内，以间隔为3进行信号重构实验.在每次实验过程中，利用Matlab软件重复运行1 000次，统计信号重构成功的次数，从而得到测量矩阵在不同稀疏度情况下信号重构成功的频率，其具体数据统计如图1所示.

图1 大小为127×16 384的测量矩阵的信号重构成功频率

其中，横轴表示信号的稀疏度数值，纵轴表示信号重构成功的频率，使用“*”标记的曲线是确定性测量矩阵的信号重构成功频率的拟合结果，而“+”标记的曲线是Gaussian随机矩阵的信号重构成功频率的拟合结果.由图1所展示的统计数据可知，在信号稀疏度k∈[13,37]时，基于伪随机序列的确定性测量矩阵的信号重构成功频率显著高于Gaussian随机矩阵，而在信号稀疏度k≥40时，确定性测量矩阵和Gaussian随机矩阵的信号重构成功频率趋近于0，即难以重构原始信号，当k<13时，确定性测量矩阵和Gaussian随机矩阵均以接近于100%的概率重构原始信号.总之，在n为奇数的情况下，基于伪随机序列的确定性测量矩阵具有更加优秀的信号重构性能.

3.2 偶数测量矩阵仿真

与奇数情况类似，当n=8时，文中将信号稀疏度设置在区间[30,72]内，以间隔为3进行信号重构实验.利用与奇数情况同样的实验方法，得到了如图2所示的统计数据.

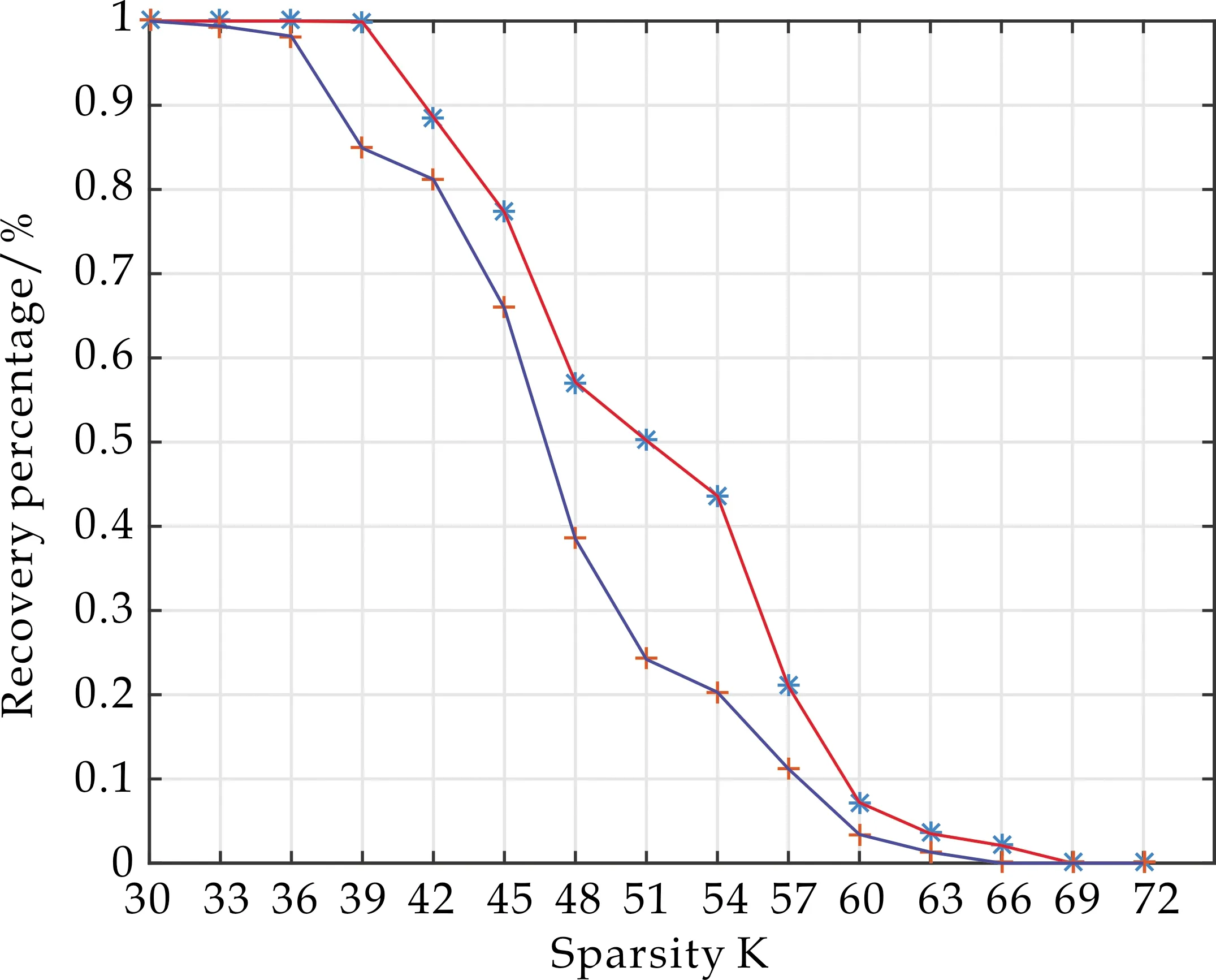
图2 大小为255×65 536的测量矩阵的信号重构成功频率

由图2可知，当信号稀疏度k∈[36,66]时，确定性测量矩阵的信号重构成功频率显著高于Gaussian随机矩阵，而当信号稀疏度k<36，确定性测量矩阵与Gaussian随机矩阵均以100%的概率重构原始的采样信号，当k>66时，确定性测量矩阵与Gaussian随机矩阵的信号重构成功频率接近于0，即难以成功重构原始信号.

综上所述，在实验仿真过程中，与Gaussian随机矩阵相比，基于伪随机序列的确定性测量矩阵具有更加优秀的信号重构性能.

4 结论

基于伪随机序列，本文分别提出了奇数和偶数情况下确定的双极性测量矩阵.通过理论推导和实验仿真，在同样条件下，与Gaussian随机矩阵相比，基于伪随机序列的确定性测量矩阵具有较低的相关性和更加优秀的信号重构性能.此外，由于具有更加简单方便的电路实现方式，所以确定性测量矩阵优于Gaussian随机矩阵.然而，文中并未考虑基于伪随机序列的确定性测量矩阵的实际应用场景，这也将是我们未来将要考虑的重要问题.