Degn-Harrison反应扩散系统平衡态解的定性分析
2021-07-21李兵方李艳玲
李兵方,李艳玲
(1.陕西铁路工程职业技术学院 基础课部,陕西 渭南 714000;2.陕西师范大学 数学与信息科学学院,陕西 西安 710119)
0 引言
1969年,Degn和Harrison提出一类经典化学反应系统,用以刻画连续培养皿中细菌Klebsiella aerogenes呼吸率的振荡行为[1].在齐次Neumann边界条件下,Degn-Harrison化学反应系统可由以下反应扩散方程组(1)表示[2],
(1)
其中,X和Y分别代表氧气和营养两种中间产物的浓度,A和B分别代表两种资源且其浓度为常数,q代表抑制强度,ki(i=1,2,3,4)是反应物的反应速率,Δ是拉普拉斯算子,Ω表示RN(N≥1)中具有光滑边界∂Ω的有界区域,∂v表示外法向导数,DX和DY是反应物X和Y的扩散系数,初始条件非负.
Degn-Harrison反应扩散系统近年来已被国内外学者广泛关注.Peng等[2]考虑经无量纲化后的一类Degn-Harrison模型的平衡态问题,借助拓扑度理论给出非常数正解存在的充分条件.基于文献[2]的研究,Li等[3]继续研究该模型,得到其Hopf分歧和稳态分歧的存在性及稳定性.Dong等[4]引入新的变量代换,考虑另一类Degn-Harrison模型,给出了ODE和PDE系统的Hopf分歧及其稳定性,文献[5]简化了文献[4]中ODE系统Hopf分歧的产生条件,文献[6]给出了该模型更细致的Hopf分歧分析.文献[7,8]分别讨论了Degn-Harrison系统的局部和整体稳定性.对具有一般反应效应的Degn-Harrison模型,文献[9]研究其斑图生成问题,建立了平衡态分歧和Hopf分歧的存在性.文献[10]给出了该推广模型的渐近稳定性分析和解的不存在性.更多关于Degn-Harrison模型及其相关问题的研究,可参考文献[11-17].
引入新的变量代换
仍记τ为t,则系统(1)可化为
(2)
本文以抑制强度c为参数, 研究系统(2)平衡态问题
(3)
正解的存在性.显然,当且仅当a>b时,系统(3)存在唯一正平衡点(u*,v*),其中

λ0=0<λ1≤λ2≤…≤λn≤…

1 正解的先验估计
本节将建立系统(3)非常数正解的先验估计及一些相关不等式性质.

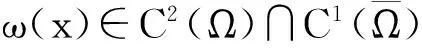


定理1设(u,v)=(u(x),v(x))是系统(3)的正解,则有

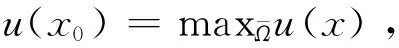
u(x)≤u(x0) 由引理1及x2,x3定义得 证毕. 若(u,v)是非常数解,则φ和ψ在Ω上变号.下面给出φ,ψ的一些相关结论. 引理2设(u,v)=(u(x),v(x))是系统(3)的非常数正解,则有 证明:令ω=d2v-d1u,则 (4) 两边同乘以ω并在Ω上积分,整理可得 (5) 因此 将式(4)两端同乘以φ并在Ω上积分得 因此 (6) 证毕. 证明:将系统(3)的第二个等式两端同乘以ψ并在Ω上积分得 由Hölder不等式得 由Poincaré不等式得 因此 整理得 由Poincaré不等式得 证毕. 同理可得 由引理3和引理4可得以下先验估计. (7) 证明:由于ω=d2v-d1u,则有 根据式(6)可得 (8) 因此 所以 (9) 即得式(7)右边不等式成立.式(8)变形可得 结合式(5)可得 利用Cauchy不等式可得 再利用Poincaré不等式可得 因此 进一步计算得 即得式(7)左边不等式成立. 证毕. 证明:利用Poincaré不等式知 注意到 证毕. 本节将给出系统(3)非常数正解的不存在性条件.首先考虑扩散系数d2对系统(3)非常数正解不存在性的影响. 证明:将系统(3)第二个方程两端同乘以ψ并在Ω上积分得 由定理1知,存在依赖于a,b,c,d的正常数M1,M2,使得 由Cauchy不等式和Poincaré不等式得 (10) 由式(9)和式(10)得 (11) 证毕. 当扩散系数d2足够小时,由定理5知,系统(3)没有非常数正解.下面的定理给出一个更强的结果: 如果λ1足够大,则对任意d2>0,系统(3)都不存在非常数正解. 证明:将系统(3)第一个方程两边同乘φ并在Ω上积分得 由于 进一步计算可得 由定理1知,存在依赖于a,b,c,d的正常数M3,使得 (12) 由Hölder不等式和Poincaré不等式得 由式(10)知 (13) 这里M=max{M3,M4}. 若固定d2>0,则当λ1(Ω)→∞时, 由极限定义知,存在正常数Λ充分大,使得当λ1(Ω)>Λ时, 证毕. 本节利用Crandall-Rabinowitz分歧定理[18],以d1为分歧参数,建立系统(3)非常数正解的存在性.这里指出,若以d2为分歧参数,在一定条件下仍可类似得到系统(3)发自平衡点(u*,v*)的分歧正解,不再赘述. (14) 令X={(u,v)∈[W2,p(Ω)]2:∂vu=∂vv=0,x∈∂Ω}和Y=[Lp(Ω)]2.定义映射F:R+×X→Y为 F(d1,U)= U=(u,v). 系统(3)的常数解相应于系统(14)的零解.显然 F(d1,0)=0. F(d1,U)关于U在零解处的Fréchet导数为 FU(d1,0)= 其所有特征值可由Lk(k=0,1,2,…)的特征值给出,其中 这里 设Lk的特征方程为 μ2-Tkμ+Dk=0, 其中 Tk=f0+g0-(d1+d2)λk, (15) 以下定理给出系统(3)分歧正解的存在性. 定理8若对任意正整数i,k≥1,当i≠k时都有d1,i≠d1,k,其中d1,k由式(15)给出,则(d1,k,0)是方程F(d1,U)=0的一个分歧点.对|s|充分小,存在方程F(d1,U)=0的一条解曲线 Γ(s)=(d1(s),(u(s),v(s))), 满足 d1(0)=d1,k,(u(0),v(0))=(0,0), u(s)=sφk+o(s),v(s)=sekφk+o(s), 其中d1(s),u(s),v(s)关于s连续可微,且 证明:根据文献[19]中单重特征值分歧定理知,若(d1,k,0)是分歧点,则须满足以下三个条件: (i)Fd1,FU和Fd1U存在且连续; (ii)dim kerFU(d1,k,0)=codimR(FU(d1,k,0))=1; (iii)令kerFU(d1,k,0)=span{Φk},则 Fd1U(d1,k,0)Φk∉R(FU(d1,k,0)). 下面逐一验证. 算子F的线性化算子为 显然,Fd1,FU和Fd1U是连续的.条件(i)满足. 当d1=d1,k时,有Dk=0,从而 kerFU(d1,k,0)=span{Φk}, dim kerL(d1,k)=1. 算子L(d1,k)的共轭算子为 类似可得 codimR(L(d1,k))=dim kerL*(d1,k)=1. 条件(ii)满足. 最后,通过计算可得 从而可得 Fd1U(d1,k,0)Φk∉R(L(d1,k)). 条件(iii)满足. 证毕. 本文针对一类具有齐次Neumann边界条件的Degn-Harrison化学反应系统,首先在代表抑制剂强度的参数c适当大时,得到氧气浓度的下界估计和营养物浓度的上界估计,进而建立了两中间产物的先验估计及一些相关不等式性质,并在此基础上给出了系统(3)非常数正解的不存在性.其次,以扩散系数d1为参数,利用分歧理论在一定扩散条件下给出了系统(3)局部分歧正解的存在性.结果表明,如果营养物扩散太慢、反应区域太小或者氧气扩散太快,系统(3)将不会出现非齐次的空间结构;而在一定扩散条件下,系统(3)将呈现空间分布不均匀的状态.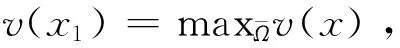


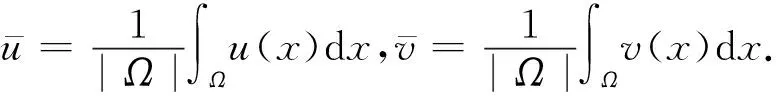





2 非常数正解的不存在性
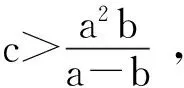
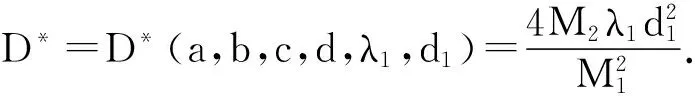




3 平衡态分歧
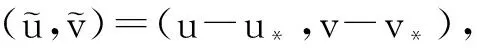
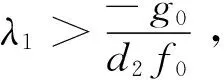



4 结论
