基于自抗扰迭代学习控制的双定子磁场调制电机转矩脉动抑制策略*

高云雷， 王玉彬， 黄 瑛

[中国石油大学(华东) 新能源学院，山东 青岛 266580]

0 引 言

磁场调制电机因具有低速、大转矩的特性，在风力发电、电动汽车等领域得到了广泛的应用[1-4]。由于固有的结构和工作原理，在带来大转矩的同时，也不可避免地带来了较高的转矩脉动。

一般而言，解决转矩脉动的方法有2大类型[5-6]:(1)改进电机的设计，如斜槽、斜极，不同齿槽数的配合，改善绕组的分布等。侧重优化电机参数，是一种减少转矩脉动现象的方法。(2)控制策略的实现，采用有效的控制方法，改善反电动势或电流波形来抑制转矩脉动。对于本文研究的场调制双定子电机，优化其结构参数后，空载电动势的偶次谐波仍然严重，导致转矩脉动变大。为了解决这些主要问题，特别是在各种高精度伺服控制系统中，需要进一步探索一种合适的控制方法，以减少由齿槽转矩和非正弦反电动势引起的周期性转矩脉动。目前，PID控制器广泛应用于电机调速系统的设计中，具有结构简单、稳定性好等优点[7-8]。然而，闭环动态品质对PID增益变化太敏感。因此，当被控对象处于经常变化的工况时，PID参数也要随之改变。另外，快速性、超调性和稳定性三者之间也存在着不可避免的矛盾。

自抗扰控制(ADRC)是一种不依赖被控对象数学模型的改进型控制算法，将外界扰动和系统内部未建模扰动统一为集总扰动，对集总扰动进行估计并给与补偿，较好地解决了快速性和超调性的矛盾[9-10]。将ADRC作为转速外环，用于永磁同步电机(PMSM)时，实现了转速响应快速、无超调的良好控制效果[11-12]。然而，ADRC中简单观测模块很难有效地抵制寄生转矩所引起的扰动。因此，对于磁场调制这类电机中转矩脉动抑制效果并不明显。解决这一问题的一种有效方法是迭代学习控制(ILC)[13-14]。ILC可以利用过去的控制输入和跟踪误差，修正某种重复运动的不理想控制信号，从而提高系统跟踪性能。传统的ILC中，需要许多完全重复的条件，如固定的时间间隔、相同的初始状态、相同的跟踪目标、相同的操作环境等。然而，在实际应用中，由于外部的未知干扰或负载的突然变化，传统迭代不变的条件往往会被破坏，这就阻碍了常规ILC的实际应用。

依据转矩/转速脉动的周期性，本文在ADRC的基础上引入ILC，该控制策略有效补偿了双定子磁场调制(FMDS)电机的转矩脉动，改善了系统动态性能。为理论分析和设计磁场调制类电机的驱动控制系统提供了一种有效方法。

1 FMDS电机的数学模型

图1为FMDS电机截面示意图，该电机由内外2个定子以及1个调磁环转子组成。FMDS电机的基本设计参数如表1所示。在FMDS电机中，原始的励磁磁动势和电枢磁动势在物理上是相互隔离的，基于磁场调制现象，调制后的励磁磁场和电枢反应磁场在内外气隙中均具有丰富的谐波。在相同的极对数和电角速度下，这些谐波会相互作用，输出稳定的电磁转矩[15]。

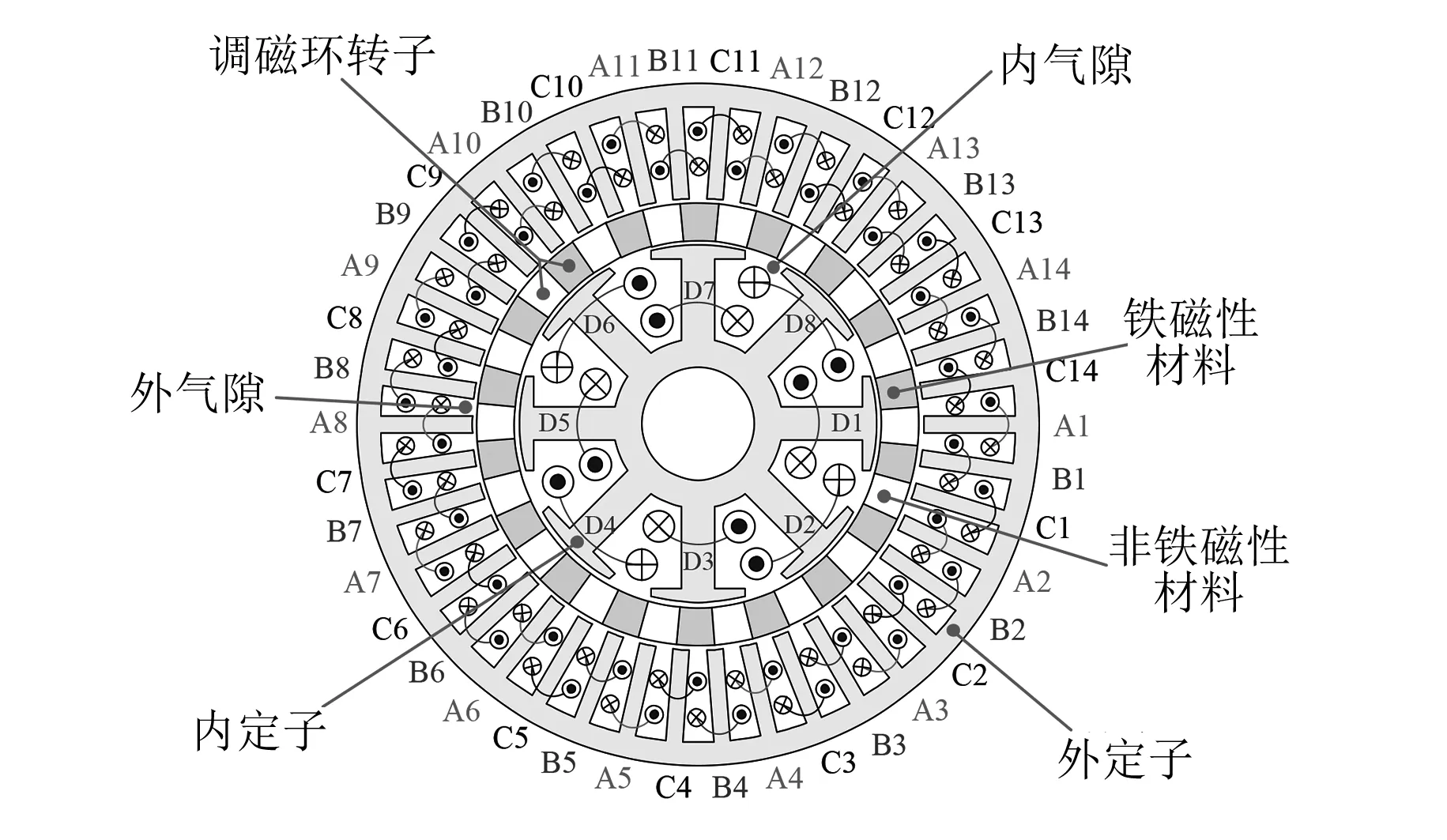
图1 FMDS电机截面示意图

表1 FMDS电机的基本设计参数

FMDS电机的动态非线性数学模型包括三相电压方程、转矩方程、机械运动方程。

其中，电压方程为

(1)

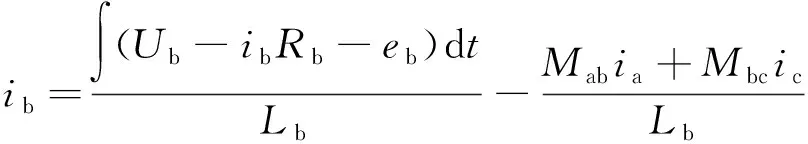
(2)

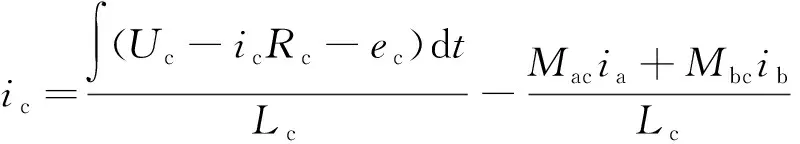
(3)

式中:Up、ip、Rp分别为p相(p对应a、b、c三相)绕组的端电压、相电流、相电阻；ep为p相绕组的空载反电动势，Lp为外定子p相绕组自感；M为两相绕组间互感。

转矩方程为

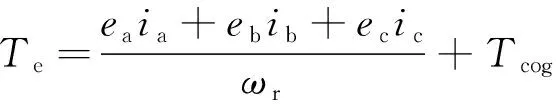
(4)

式中:Te为电磁转矩;ωr为调磁环转子机械角速度;Tcog为齿槽转矩。

机械运动方程为

(5)

式中：J、B、Tl分别为系统转动惯量、摩擦系数、负载转矩。

2 转速脉动分析

由于FMDS电机特殊的结构，内、外气隙谐波磁场中含有丰富的谐波成分，进而导致非正弦反电动势。当通入正弦电枢电流时，会产生比较严重的转矩脉动。abc坐标系下反电动势的正序分量uabc(1)和负序分量uabc(2)可分别表示为

(6)

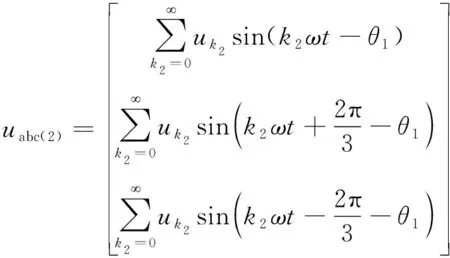
(7)

变换到dq坐标系下,反电动势的正序分量udq(1)和负序分量udq(2)分别为

(8)

(9)

由此可知，将abc坐标系下的反电动势谐波分量变换到dq坐标系中，第k次正序分量将变成dq坐标系中的第k-1次分量，第k次负序分量将变成dq坐标系中的第k+1次分量。因此，在dq坐标系中，相应的转矩谐波将以某一次数的倍数出现，即可表示为

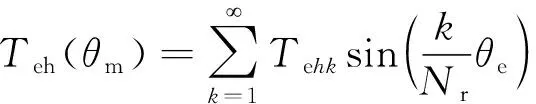
(10)

式中:θm为转子的机械角度;θe为电角度;θe=Nrωrt=Nrθm；Tehk为傅里叶系数；Nr为调磁环转子极对数。

另外，内、外定子齿槽的存在，使不同位置磁路上的磁阻存在差异，气隙磁场在空间分布上出现锯齿波，进而引起转矩脉动，这部分转矩被称为齿槽转矩。根据文献[16]的分析，齿槽转矩可以被建模为转子位置的函数，该函数依赖于定子槽的数目和转子极对的数目：

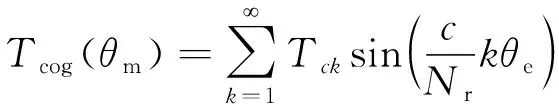
(11)

式中：Tck为傅里叶系数；c为定子齿数和转子极对数之间的最小公倍数。

大雨下了整整一晚，户外的一切都被雨水冲涮得露出底色。迟恒醒来时雨仍在下，头顶的铅云漫无边际，而且不向任何方向作丝毫的飘移，仿佛这座小镇是它这趟旅行的终点。

由式(5)可得FMDS电机中调磁环转子机械角速度与电磁转矩之间的传递函数：

(12)

由此可知，转矩谐波将引起相同阶次的速度谐波：

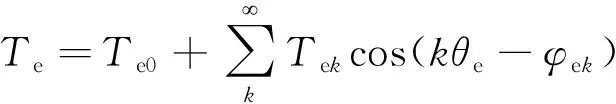
(13)

(14)

式中:Te0为平均转矩；ωr0为平均转速；Tek和φek分别为第k次转矩谐波的幅值和相角；ωrk和φrk分别为第k次转速谐波的幅值和相角。

联立式(5)、式(13)和式(14)可得：

Te0-Tl=Bωr0

(15)

Tekcos(kθe-φrk)=Bωrkcos(kθe-φrk)-

kJPωrωrksin(kθe-φrk)

(16)

Bωrkcos(kθe-φrk)-kJNrωrωrksin(kθe-φrk)≈

Bωrkcos(kθe-φrk)-kJNrωr0ωrksin(kθe-φrk)≈

(17)

考虑到B比kJNrωr0小得多，ωrk比ωr0小的多，式(16)可以简化为

Tekcos(kθe-φmk)≈

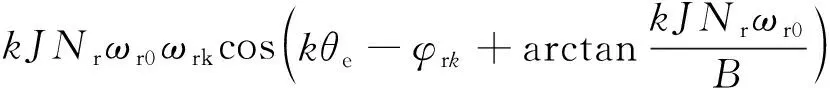
(18)

由此可知，转矩脉动与转速脉动二者均具有明显的周期性，并且第k次的转矩谐波幅值与转速谐波幅值成正比。

3 控制器的设计

由于FMDS电机本质上具有正弦空载反电动势波形，为了获得高性能驱动，本文选择矢量控制(FOC)作为主要控制策略。此时，根据电压方程、转矩方程以及机械运动方程整理后的状态方程为

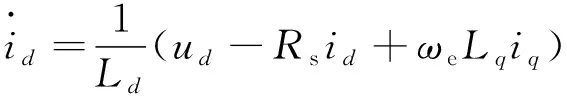
(19)

(20)

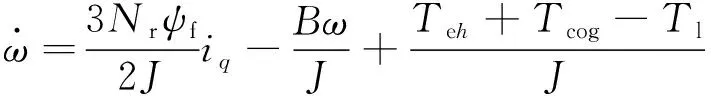
(21)

式中:ud、uq分别为外定子d、q轴的电压;id、iq分别为d、q轴上的定子电流;Ld、Lq为d、q轴电感，由有限元分析可得，d轴电感与q轴电感非常接近，即Ld=Lq=L;ωe为电角速度，ωe=Nrωr;ψf是内定子励磁磁场与外定子电枢绕组交链形成的磁链。

图2为FMDS电机的调速系统框图，考虑到系统对电流环的实时性有较高的要求，电流环仍采用PI控制器。由式(21)，可知速度环表示为一阶系统数学模型，因此，速度环采用一阶ILC-ADRC。图3为所提出的ILC-ADRC结构框图，主要由微分跟踪控制器(TD)、线性扩张状态观测器(LESO)、ILC和状态误差反馈控制律(SEF)4部分组成。

图2 FMDS电机的调速系统

图3 ILC-ADRC策略框图

传统的PI控制直接以电机的给定转速参考值与输出转速的差作为控制信号，造成了电机输出响应速度与超调之间的矛盾。为此，引入TD，通过为参考给定值安排合理的过渡过程，可以实现输出转速的快速无超调响应。TD的设计具体为

(22)

LESO模块可以实时地对电机输出转速进行观测，同时引入一个扩张状态对电机内部扰动和外部扰动进行实时观测，线性状态观测器的设计具体为

(23)

式中:z1为电机输出转速ω的实时观测值；z2为电机内部扰动和外部扰动的实时估计值；β1、β2为可调节参数，其可通过扩张状态观测器带宽进行整定。

ILC是一种基于先前存储的控制输出信息和当前误差信息的误差校正算法。在ILC模块中，选择P型ILC，由PCF和CCF2部分循环反馈构成，实现简单且在CCF的镇定作用下，PCF可期望快速实现跟踪任务，有效提高系统跟踪性能。由式(18)可知，转矩脉动源可以从转子转速中实时观测到，因此，可以利用转速误差信息来抑制转矩脉动，建立基于转子位置角度的迭代学习率。其中，迭代学习率为

iq_c,k+1(θ)=(1-α)iq_c,k(θ)+Gpω2,k+Gcω2,k+1

(24)

式中：k为迭代次数，iq_c,k+1(θ)为ILC输出q轴的补偿电流；ω2，k、ω2，k+1分别为第k、k+1个迭代周期的转速误差；Gp、Gc分别为ω2,k、ω2,k+1的学习增益，Gp较小将导致学习收敛速度较慢，Gp过大将破坏学习收敛条件，而当存在时滞时，Gc过大将导致振荡响应；α为遗忘因子，0<α≤1，在实现过程中引入了遗忘因子，避免信号中的噪声和非周期性成分的累加，提高了系统的鲁棒性和抗干扰性能。

SEF以转速的平方差作为反馈控制量，通过对误差进行放大，加快输出转速ω对给定值的跟踪，进而加快系统的响应速度。同时根据LESO对系统内扰和外扰的实时估计值对系统进行实时补偿，从而提升系统的抗干扰能力。SEF的设计具体为

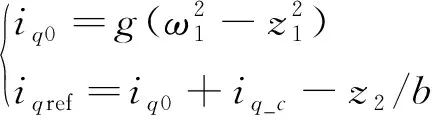
(25)

式中:b为补偿系数，其取值会影响系统的动态性能;g为误差反馈系数。

当b增大时，ILC-ADRC的补偿强度减弱，系统动态动态性能降低。而当b减小时，补偿强度加强，系统动态性能提高。因此，选取合适的参数b对ILC-ADRC控制性能的实现也很重要。

4 仿真及分析

为了验证ILC-ADRC对FMDS电机的控制效果，首先利用电磁分析软件JMAG对FMDS电机进行有限元计算分析。

通过有限元计算分析得到FMDS电机在不同运行点下的空载反电动势、自感和互感等相关电磁参数，同时得到不同转子位置下的齿槽转矩。结合式(1)～式(5)在MATLAB/Simulink平台下对FMDS电机进行建模，并搭建基于ILC-ADRC的FMDS电机调速系统仿真模型。其中，控制器主要参数如表2所示。

表2 控制器主要参数

为了说明所提控制策略的有效性，将其与传统的PI控制方法进行了比较。分析FMDS电机的稳态性能，图4～图6分别为额定工况(n=167 r/min,Tl=4 N·m)下2种策略的转速、转矩和电流稳态仿真对比结果。在图4中，加入ILC-ADRC后，转速的脉动从5 r/min降低到了2 r/min，转速波形更加平稳。图5给出了同时刻下的转矩波形，传统PI控制策略中，FMDS电机的转矩脉动较大。而在ILC-ADRC策略下，转矩的脉动从0.8 N·m降低到了0.3 N·m，相应的转矩脉动系数(TRF)从20%降低到了7.5%，明显降低了转矩脉动。同时，对比图4(a)和图5(a)可以发现，转速和转矩脉动呈现近似一致的周期性。图6为三相电流波形，可以注意到，在ILC-ADRC策略下，电流谐波成分增加，非正弦程度增加，由此可知，某些电流谐波的加入，与反电动势作用生成与干扰反向的转矩分量，抵消了部分转矩谐波。

图4 转速波形

图5 转矩波形

图6 三相电流波形

最后，为了验证系统的动态性能，图7和图8给出了转速、转矩波形变化，包括带载起动、转速突变以及负载突变。可以看出，在FMDS电机起动时，选择合理的控制参数，PI策略下的转速超调较小，然而在转速突变到额定转速时，超调量明显增大。相同的工况下，ILC-ADRC策略下的转速均无超调，并能够在极短的时间内收敛到最优转矩脉动。另外，在负载发生突变时，ILC-ADRC策略的抗干扰能力明显优于PI策略。

图7 基于PI策略的动态仿真

图8 基于ILC-ARDC策略的动态仿真

5 结 语

本文提出并实现了一种ILC-ADRC的转矩脉动抑制策略。与传统矢量控制相比，所提ILC-ADRC策略能够实现转速响应快速、无超调，且将转矩脉动从20%降低到了7.5%，有效抑制了转矩脉动。仿真结果验证了所提出ILC-ADRC控制策略的有效性。