基于查表法的电励磁双凸极电机建模研究*
2021-07-20明庆永陈志辉封成双
明庆永, 陈志辉, 封成双
(南京航空航天大学 自动化学院,江苏 南京 211100)
0 引 言
电励磁双凸极电机(DSEM)是20世纪90年代提出的一种新型无刷直流电机[1-2],在开关磁阻电机的基础上发展而来[3-4]。其定转子呈双凸极结构,定子上安装有电枢绕组和励磁绕组,转子无绕组。DSEM因具有结构简单、可靠性高、励磁可调、控制灵活等优点,获得了广泛关注[5]。
由于DSEM定子与转子均呈现凸极结构,磁场的边缘效应和饱和现象也比较严重[6],其电感等参数也随着电机运行状态不同而变化。DSEM电枢绕组与励磁绕组间的互感使磁场分布更为复杂,电枢电流对电感波形影响的分析也更加困难[7-8]。关于DSEM建模的研究较少,对其进一步深入研究具有较大实用意义。DSEM建模方法可分为近似线性建模和非线性建模,多数研究主要是对DSEM电感进行建模。文献[9-10]对电感进行分段线性近似,将等效电感建模法运用于DSEM。文献[11]将一个周期内电感曲线分为6段,分别用正弦函数和直线近似拟合各段电感曲线,将其依次相连,即可构造连续可导的分段线性电感模型。以上所述近似线性建模方法均是在忽略磁饱和影响,不考虑电感随电流发生变化的前提下建立的,因此所建模型误差较大。双凸极电机实际模型呈高度非线性,在近似线性方法基础上,形成精度较高的非线性建模方法,能够更精确地反映实际电磁关系。文献[12]提出自适应模糊神经网络建立双凸极永磁电机模型的方法,采用改进的递推最小二乘法修改网络参数,同时采用遗传算法对遗忘因子和学习率进行了优化。文献[13]将基于T-S模糊推理的模糊神经网络模型应用于DSEM非线性建模中,考虑了磁路的局部饱和效应的影响。模糊神经网络建模方法是用模糊神经网络来逼近各相磁链与励磁电流、相电流及转子位置角之间的非线性关系。其模型逼近精度与隶属度函数中模糊子集个数有密切关系,个数越多,逼近精度越高,但同时模糊推理模型中的规则数及参数也随之急剧增加,训练时间大大增加。文献[14]利用获得的绕组自感和磁链数据,基于Look-up table模块,查询不同转子位置角度对应的自感及磁链的值,搭建了基于MATLAB/Simulink的电机模型。文献[15]通过分析DSEM自身电感特性以及励磁磁场与电枢反应对电感的影响,拟合出了同时考虑励磁电流和电枢电流的影响系数,建立了Lp及Lpf的模型。此外,有限元法是目前主流的非线性建模方法。文献[16-18]通过有限元仿真的方法对电机的磁链、感应电动势等进行仿真,具有仿真结果准确的优点。但是有限元仿真耗时长,仿真效率低。
为了便于电机控制策略的选取及控制参数的整定,提高仿真效率,本文利用三维查表法建立了DSEM模型。在深入分析DSEM电磁特性基础上,利用有限元法建立了磁链特性ψp(ip,if,θ)与转矩特性Tp(ip,if,θ)的三维数据表。基于电压、磁链和转矩方程,并考虑励磁磁链的影响搭建了DSEM磁链和转矩模型,不仅解决了电枢绕组电压方程的建模问题,也解决了励磁绕组电压方程和电磁转矩精确建模的两大问题。同时,将仿真结果与有限元法比较,以验证所建模型的准确性。最后,利用本文方法所建模型仿真分析了励磁电流采用滞环控制时的空载反电动势特性以及电枢电流采用不对称电流控制策略时的电流特性,并与有限元及试验测试结果相比较,验证了本文建模方法的有效性,并为该类电机后续闭环控制研究奠定基础。
1 DSEM结构及电磁特性分析
1.1 DSEM基本结构
本文研究内容是基于一台1 kW的四相8/6极DSEM展开的,转子极宽度比定子极宽度机械角加宽5°。图1给出了四相8/6极DSEM的剖面图。该电机的主要结构和绕组数据如表1所示。
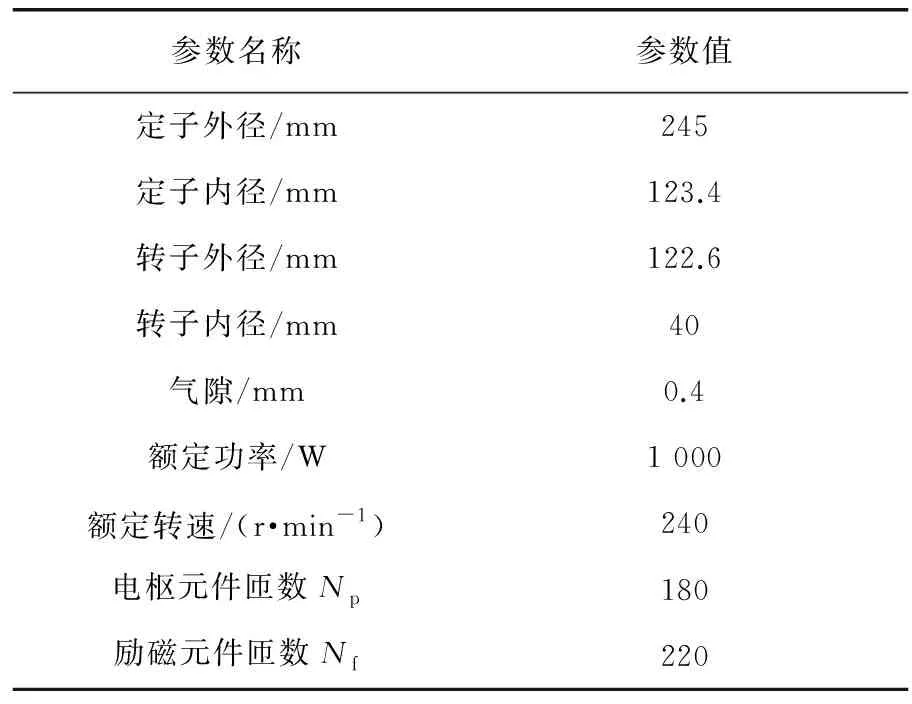
表1 8/6极四相DSEM主要参数

图1 剖面图
该四相DSEM共有8个定子极, 6个转子极。8个定子齿构成了6个小定子槽和2个大定子槽。小槽中仅放置电枢绕组,大槽中放置电枢绕组和励磁绕组,相对的2个定子极上的电枢绕组串联构成一相,分别形成A相、B相、C相和D相。电枢绕组和励磁绕组之间存在电磁耦合关系。图2为8/6极DSEM展开图,沿着转子旋转方向,电枢绕组相序为C→B→A→D。本文定义电机正方向为逆时针旋转方向。
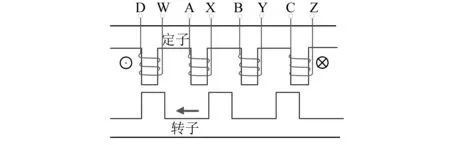
图2 展开图
1.2 DSEM电磁特性分析
DSEM每相绕组匝链的磁链由电枢绕组与励磁绕组间互感磁链、电枢绕组相间互感磁链以及电枢绕组自感磁链构成,是关于电枢电流、励磁电流以及转子位置角的函数应变量。以A相为例,其表达式为
ψa(ia,ib,ic,id,if,θ)=ψaf+ψaa+ψab+ψac+ψad=
Lafif+Laia+Labib+Lacic+Ladid
(1)
由图3可以看出,与电枢绕组与励磁绕组间的互感Laf以及电枢绕组自感Laa相比,电枢绕组之间的互感Lab很小,因此相间互感磁链可以忽略不计,即A相磁链可以简化为
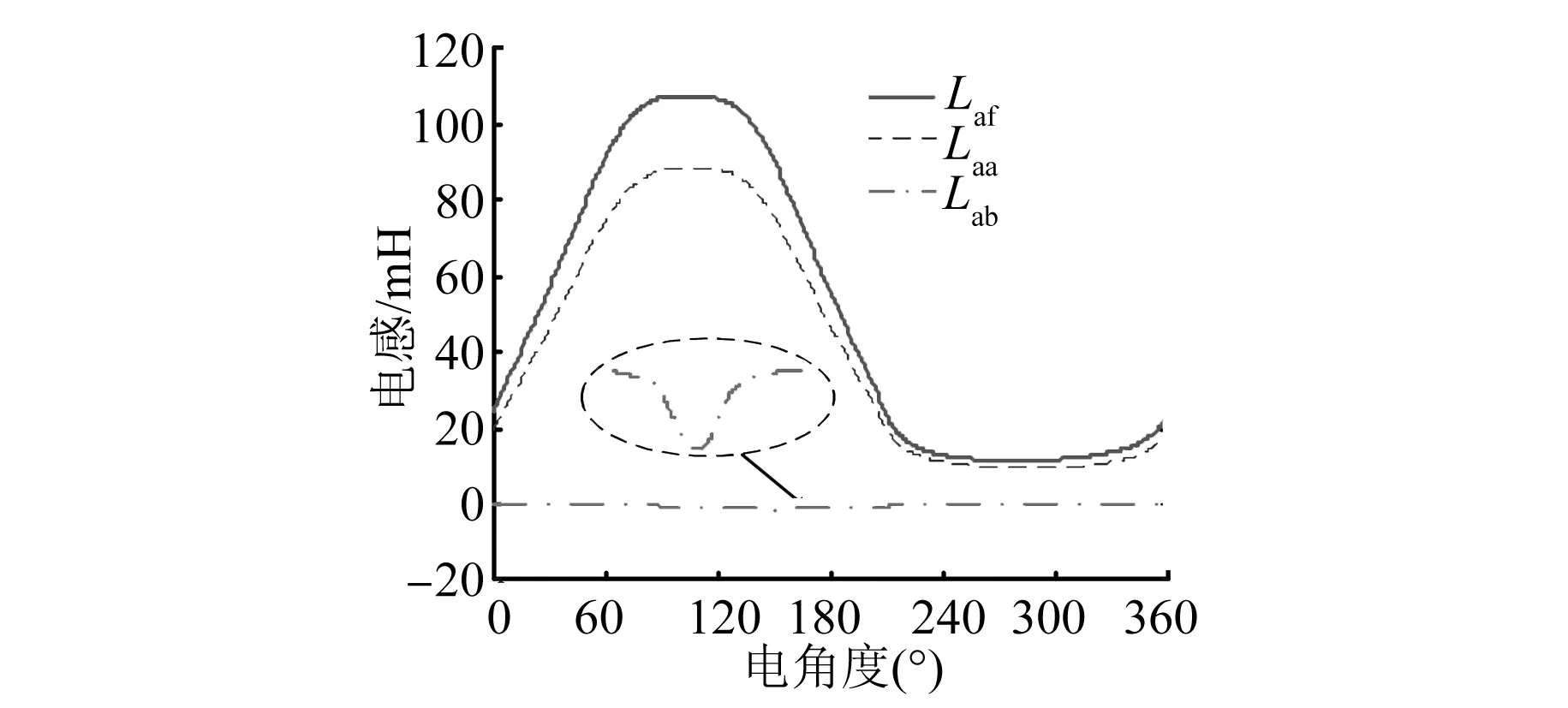
图3 电感波形
ψa(ia,if,θ)=ψaf+ψaa
(2)
由式(2)可知,相磁链是关于对应相电枢电流、励磁电流及转子位置角的应变量,三者作为输入量即可确定对应状态的输出磁链。
同理,励磁磁链的计算式为
ψf=Lfaia+Lfbib+Lfcic+Lfdid+Lfif
(3)
由图1可知,穿过F+—F-平面的磁通即为励磁绕组在转子侧的磁通量。根据磁通的连续性,则该磁通在定子侧分别进入A、B、C、D各相定子。若忽略通过定子槽较小的励磁漏磁通,则:
φf=φa+φb+φc+φd
(4)
式中:φa、φb、φc、φd分别为A、B、C、D相与励磁匝链的磁通;φf为励磁磁通。
由磁通与磁链的关系,可得知励磁磁链表达式为
ψf=(ψa+ψb+ψc+ψd)×Nf/Np
(5)
式中:Nf和Np分别为励磁绕组匝数和电枢绕组匝数。
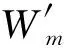

图4 DSEM磁场储能与磁共能

(6)

(7)

(8)
根据机电能量转换原理可知,四相DSEM是一个多边激励系统,其激励分别为电枢激励和励磁激励,即磁共能表达式为

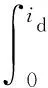
(9)
将式(9)代入式(8)可得:
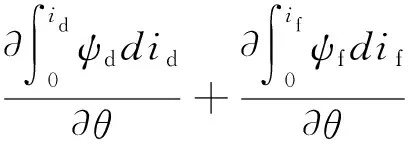
(10)
即有:
Te=Ta+Tb+Tc+Td+Tcog
(11)
式中:Ta,Tb,Tc,Td分别为A、B、C、D各相励磁转矩与磁阻转矩之和。Tcog为电枢电流为零,仅通入励磁电流产生的齿槽转矩。由式(11)可知,当只有A相通入电流时,电机单相输出转矩TeA为
TeA(ia,if,θ)=Ta+Tcog
(12)
2 非线性建模
有限元法是目前对DSEM进行数学分析的主流手段,具有结果准确的显著优点,但其耗时长,仿真效率低。依据第1节理论分析可知,DSEM非线性数学模型由磁链方程、电压方程和转矩方程构成。由于DSEM高度非线性和强耦合性,采用常规拟合方法进行建模,过程较为复杂。本文采用查表法,依据式(2)和式(5)分别建立相磁链和励磁磁链模型。依据式(12)建立其单相转矩模型,各单相转矩叠加后,对多余的齿槽转矩进行扣除,即可得到电磁转矩。
DSEM电压方程为
um=imRm-em
(13)
反电动势方程为

(14)
式中:m=a,b,c,d,f。依据式(13)和式(14)建立其电枢绕组和励磁绕组电压模型。
利用有限元仿真软件ANSYS Maxwell 2D对电机进行建模和仿真,对电机运行过程中瞬时参数计算,主要包括磁链、转子位置角、转矩等。在获得磁链和转矩数据后,对其建立输入量为电枢电流、励磁电流及转子角位置、输出量分别为磁链和单相转矩的数据表格,并通过Simulink平台中2-D Look-up table模块进行数据查表,输出对应控制状态下的磁链和单相转矩,建模总体过程如图5所示。

图5 DSEM非线性建模总体过程框图
2.1 有限元仿真数据获取
利用有限元仿真软件ANSYS Maxwell 2D建立电机模型,并通过静态仿真得到磁链及电磁转矩数据表。在电枢与励磁绕组施加不同激励电流,电枢电流为-10~20 A,电枢电流增量Δip设置为2 A;励磁电流为0~10 A,励磁电流增量Δif设置为1 A;转子角位置角增量Δθ设置为0.6°。磁链数据与转矩数据获取流程图如图6所示,分为三层循环,分别为外层励磁电流循环、中间层电枢电流循环、内层转子位置角循环,最终获得不同励磁电流、不同电枢电流和不同转子位置角组合下对应的磁链与转矩值。不同状态下对应的磁链和转矩曲面图分别如图7和图8所示。

图6 磁链与转矩数据获取流程图
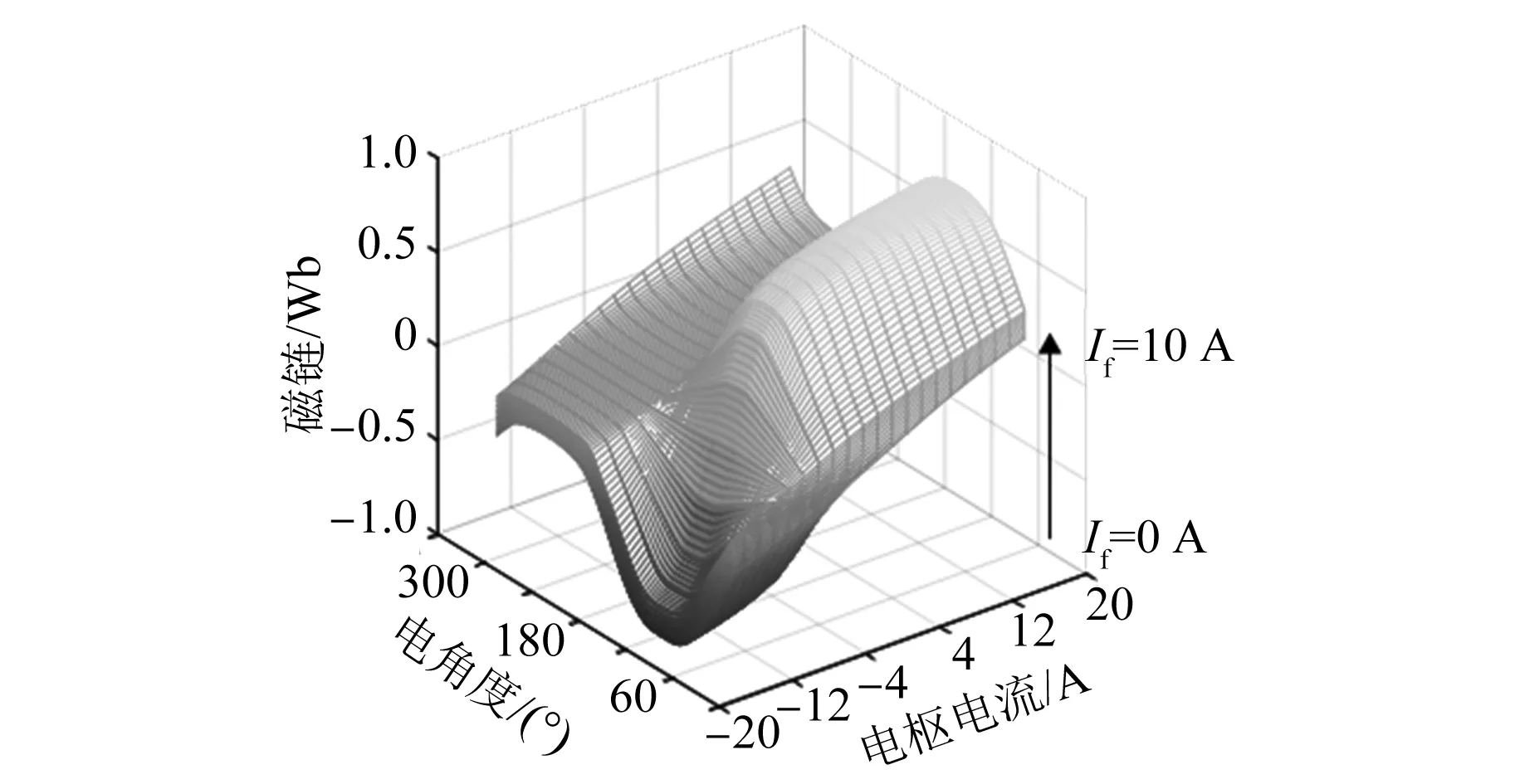
图7 不同状态下磁链曲面图

图8 不同状态下转矩曲面图
2.2 MATLAB/Simulink电机模型建立
2.2.1 磁链模型
由于各相磁链是关于对应相电枢电流以及励磁电流和转子位置角的应变量,因此可通过三维查表的方式得到各状态下的磁链。将有限元仿真获取的数据导入3-D Look-up table模块,建立三维数据表。然后根据转子位置角θ、电枢电流ia和励磁电流If3个输入量,查表输出对应的相磁链ψp,如图9所示。由于在采用有限元软件仿真时,各输入量增量不可能接近无穷小,因此有限元计算得到的磁链仍然是离散的量。为了得到DSEM在任意状态时的磁链值(电流、转子位置角均在索引范围内),需要对获取的磁链数据进行插值计算。根据式(14),对查表磁链值进行微分计算,即可得到绕组反电动势。分别采用有限元法与查表法计算得到磁链比较波形及反电动势比较波形如图10所示,二者磁链最大误差仅为0.6%,空载反电动势最大误差为3.2%,误差产生主要原因是本文建模忽略了相绕组之间的互感。

图9 相磁链模型

图10 磁链与空载反电动势波形比较
除了电枢绕组磁链模型,本文还考虑了励磁绕组磁链,依据式(5)搭建励磁绕组磁链模型,如图11所示。

图11 励磁磁链模型
2.2.2 转矩模型
输出转矩也是关于电枢电流、励磁电流及转子角位置的函数应变量,因此也可采用与磁链模型相同的查表法输出A相转矩, A相转矩模型如图12所示。B、C、D相转矩通过相位关系得到,机械转子角位置分别滞后A相15°、30°和45°。图13为单相转矩波形对比图,单相转矩最大误差为1.2%,可以发现,二者吻合度很高,验证了该环节的有效性。

图12 A相转矩模型
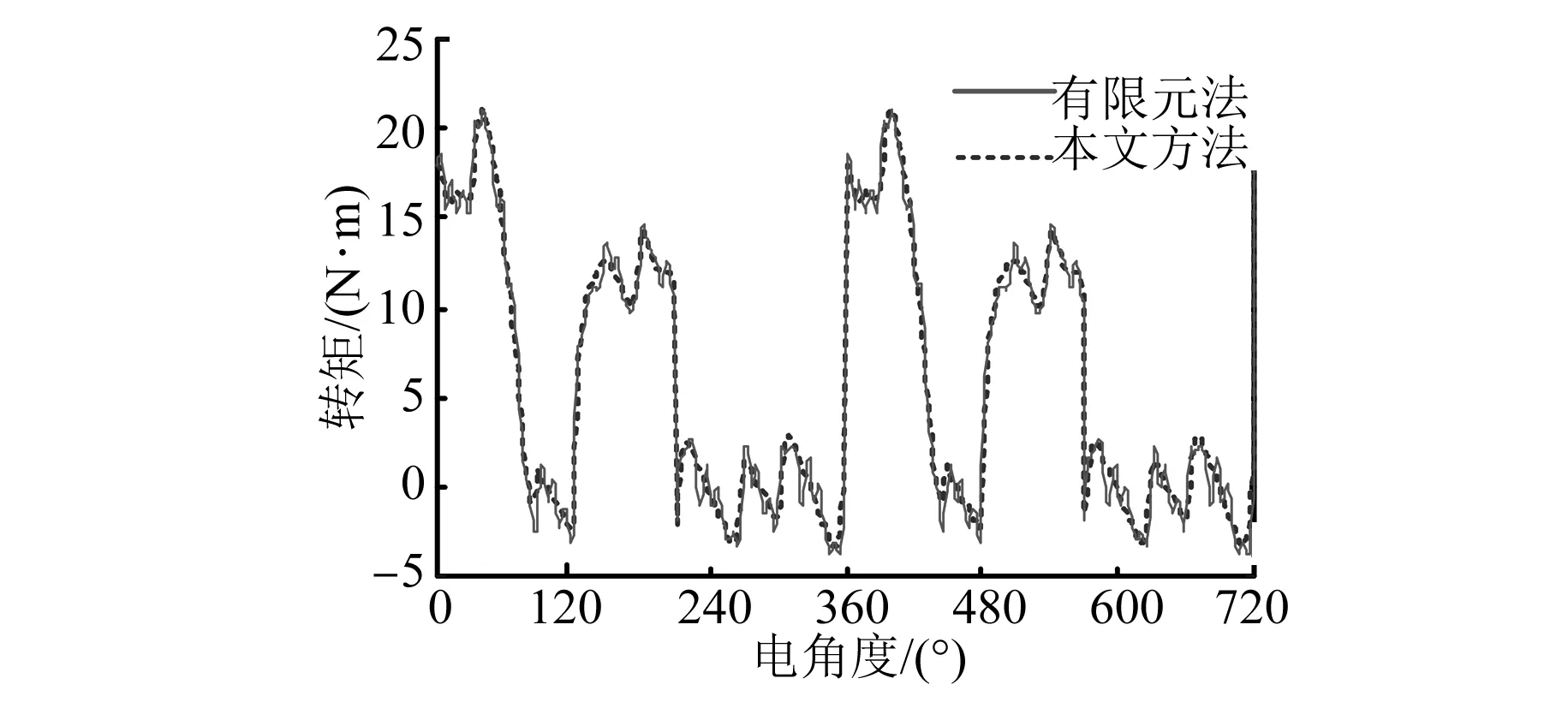
图13 单相转矩波形对比
但是需要注意,若将Simulink查表插值计算得到的单相转矩直接进行叠加得到的电磁转矩与有限元计算得到的电磁转矩存在一定的差异性,如图14所示。从二者波形对比可以看出,2条曲线差异较大,Simulink插值法得到的转矩幅值要明显小于有限元法所得到的结果。从表2可以看出,当电机处于“空载”状态时,2种建模方法计算得到的平均转矩误差最大。由式(12)可知,这是因为将Simulink插值法计算得到的各单相转矩叠加,导致电磁转矩重复计算了4次齿槽转矩Tcog。因此,需要对多余的齿槽转矩进行扣除。
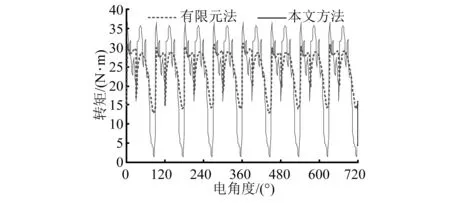
图14 扣除前输出转矩波形对比

表2 平均转矩比较及误差
将每相的齿槽转矩之和的3/4倍作为电磁转矩的扣除量,转矩扣除模块如图15所示。多余齿槽转矩扣除后的电磁转矩波形对比如图16所示。从对比结果来看,2种方法得到的波形吻合程度较高。不吻合现象主要发生在转矩峰值处,这是因为在建模时为了合理简化电机模型,认为各相是对称的,只对A相绕组通入电流得到查表数据,但实际上电机各相并非完全对称,因此产生了较小的误差。
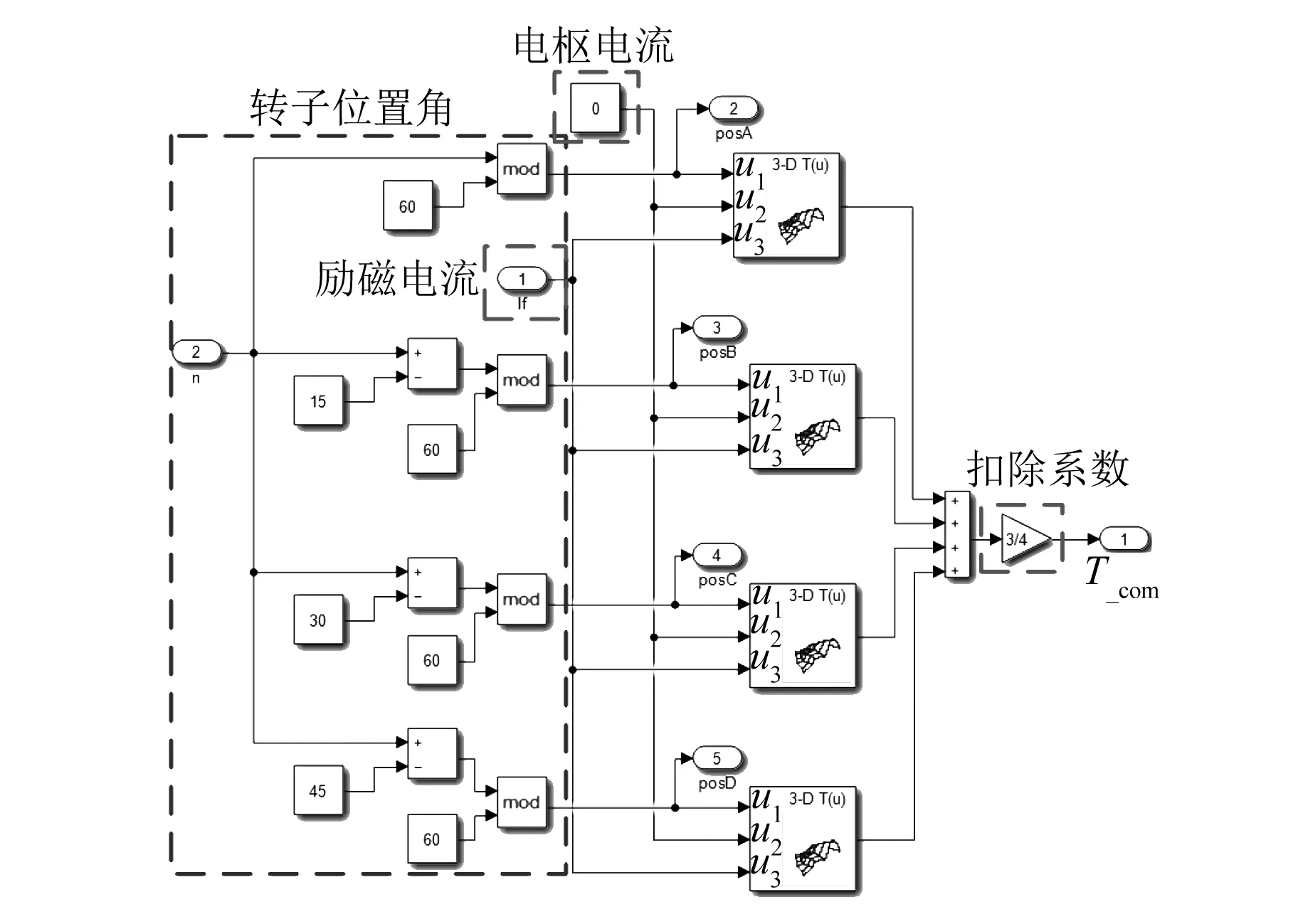
图15 齿槽转矩扣除模块
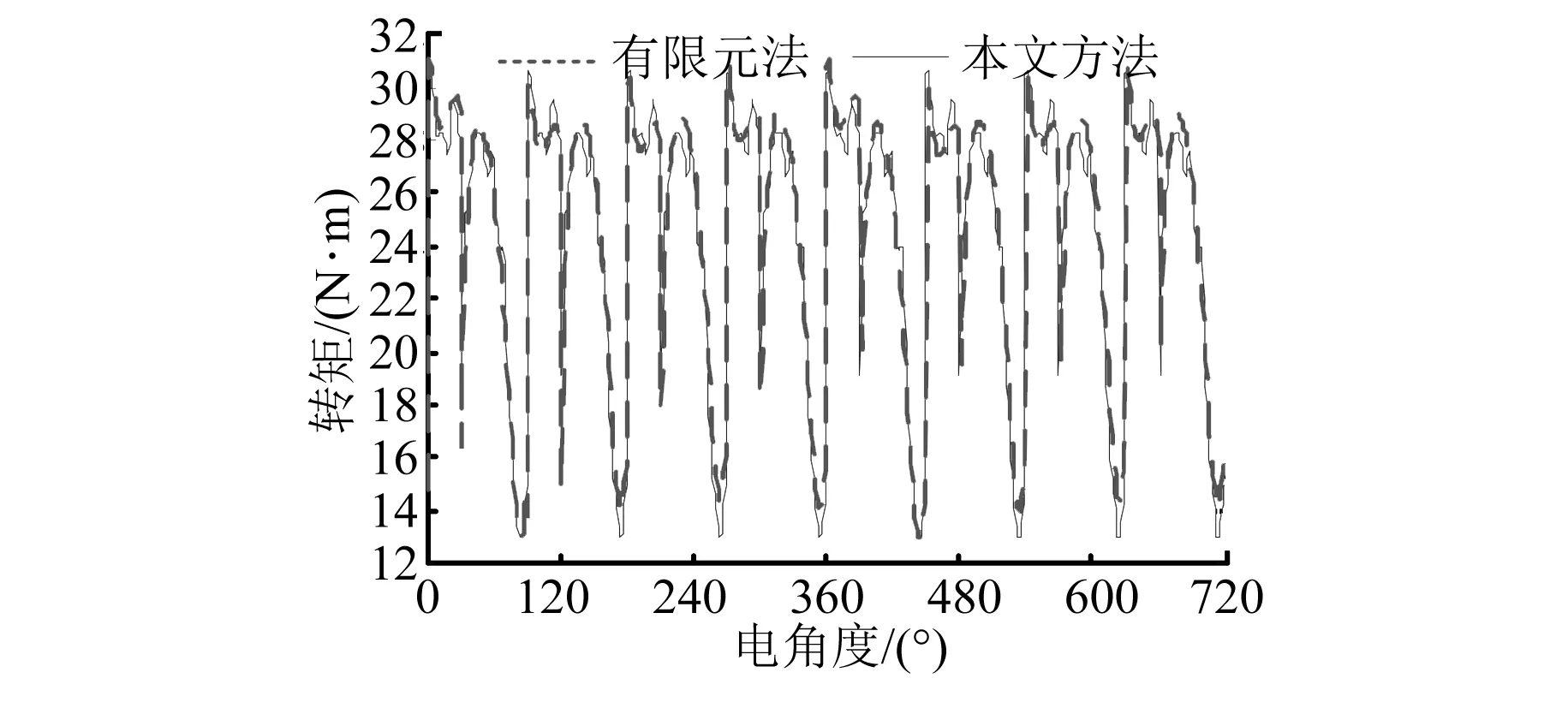
图16 扣除后电磁转矩波形对比
从图17可以看出,不同激励情况下,2种方法得到的转矩平均值误差较小,平均误差不超过3.4%,波形吻合度较高,能够满足DSEM控制仿真分析的使用场景。

图17 不同激励输出平均转矩对比
3 模型验证
3.1 模型仿真
为了进一步验证所搭建电机模型的准确性,对不同工作状态下的仿真结果进行对比。当励磁电流采用滞环控制时,励磁电源电压设置为120 V,励磁电流环宽为0.4 A,在额定转速下,对比有限元法与本文方法所建模型的空载反电动势仿真波形。
从图18可以看出,当励磁电流采用滞环控制时,有限元法与本文方法所建模型的空载反电动势波形相一致。

图18 空载反电动势波形对比(n=240 r/min)
当电枢电流采用不对称电流控制策略时,对比有限元法与本文方法的仿真结果,如图19所示。
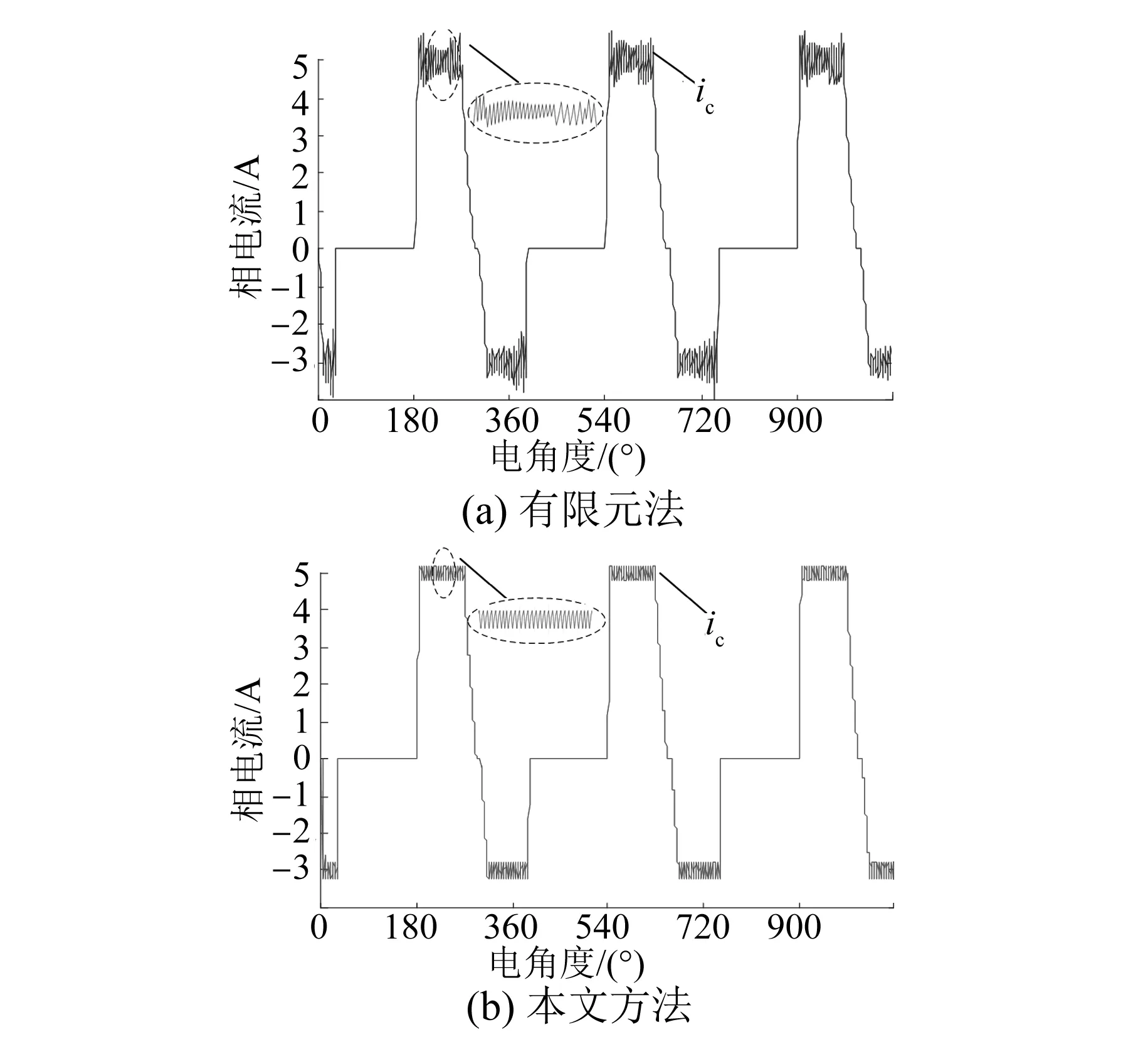
图19 相电流波形(n=240 r/min)
正向电流幅值为5 A,负向电流幅值为3 A,电枢电流采用滞环斩波的方式,环宽设置为0.4 A。可以看出,由于电感的存在,电枢电流在上升和下降阶段均不能突变,存在一定的斜率。2种方法仿真得到的相电流波形变化规律一致。
本文仿真所采用计算机处理器为i7-8700 CPU @3.2 GHz,运行内存为8G。由表3可以看出,对空载反电动势进行3个电周期的仿真,采用有限元法仿真耗时约134 min 50 s,而采用本文方法所建模型进行相同仿真耗时45 s。当电机输出平均转矩为20 N·m时,有限元法和本文方法耗时分别为171 min 37 s和1 min 19 s。在保证仿真精度的基础上,使用本文方法进行仿真,极大地缩短了耗时,提高了仿真效率。

表3 仿真耗时对比(3个电周期)
3.2 试验验证
为了进一步验证模型与实际电机的吻合程度,利用试验平台对其空载反电动势及不对称控制相电流波形进行实际测量,试验平台如图20所示。

图20 试验平台
试验条件为,电机转速为240 r/min,电枢与励磁功率变换器母线电压电压均设置为120 V,滞环环宽均设置为0.4 A。电枢电流采用不对称控制策略,正向电流幅值为5 A,负向电流幅值为3 A。图21(a)为空载反电动势试验波形,图21(b)为不对称相电流试验波形,可以看出,试验结果与仿真结果一致,再次验证了所搭建模型与实际电机模型的高度吻合性。
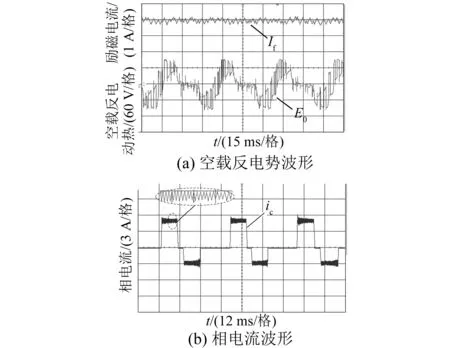
图21 试验波形
4 结 语
本文从机电能量转换的角度深入分析了DSEM电磁特性。由于DSEM存在明显的边缘效应和高度的局部饱和现象,其磁链和转矩均为电枢电流、励磁电流、转子位置角的非线性函数,难以采用常规方法建立精确的模型。现有文献大多集中于非线性电感和相磁链模型的建立。本文在相磁链查表研究基础上,根据其数学关系得到了励磁磁链。不仅解决了电枢绕组电压方程的建模问题,同时也解决了励磁绕组电压方程和电磁转矩精确建模的两大问题,也是本文主要的创新之处。本文方法所建模型主要优点如下:
(1) 采用查表法同时对相绕组和励磁绕组磁链进行建模,仿真精度高,与有限元法相比,最大误差仅为0.6%,二者空载反电动势最大误差为3.2%,波形吻合程度较高。
(2) 采用查表法搭建了单相转矩模型,单相转矩最大误差为1.2%。在得到单相转矩的基础上,将各相转矩进行叠加,并扣除多余齿槽转矩,得到电磁转矩。电磁转矩平均值最大误差3.9%,且波形吻合度高。
(3) 耗时短,仿真效率高。分别采用有限元法与本文方法对其空载反电动势进行仿真。耗时分别为134 min 50 s,本文方法所建模型耗时仅为45 s,用时仅为前者的1.2%。当输出转矩为20 N·m时,有限元法与本文方法仿真耗时分别为171 min 37 s和1 min 19 s,用时仅为前者的1.3%。大大提高了仿真效率,便于控制策略的选取与控制参数的整定。
(4) 本文建模方法原理简单,适用范围广。对于相间互感较小的三相、五相等DSEM以及开关磁阻电机的建模具有普适性和实用性。
