基于模型预测的PMSM速度环PI自整定控制

彭颖涛， 陆 可

(西南交通大学 电气工程学院，四川 成都 611756)

0 引 言

永磁同步电机(PMSM)具有体积小、效率高、功率密度大等特点，广泛应用于工业和交流传动领域。其中矢量控制因为直流电压利用率高、电流谐波分量小等特点受到广泛关注[1]。模型预测控制(MPC)是一种比较先进的基于模型的控制方法，主要分为连续集模型预测控制(CCS-MPC)和有限集模型预测控制(FCS-MPC)。FCS-MPC算法省略了脉冲宽度调制环节，直接产生开关信号，控制更加简单快速，且比矢量控制可以得到更好的动态响应性能[2]。

传统模型预测电流控制，通过离散化电流状态方程选取最优成本函数所对应的开关状态作为输出。由于性能表现一般，牛里等[3]提出鲁棒电流预测算法，进而提高电机鲁棒性。模型预测磁链控制，通过对模型预测转矩控制进行改进，将求解转矩和磁链幅值的目标函数转化为求磁链矢量的方式来避免权重系数难以设计的问题[4-6]。

在PMSM运行过程中，难以避免的会因为工作状况或外界环节的改变而产生不同程度的扰动，影响电机的动静态响应性能。王喜莲等[7-8]为降低转矩波动，针对电流环采用小信号分析法、典型Ⅰ型系统整定法设计PI参数自适应调节器。王莉娜等[9-10]则针对传统双闭环控制系统，从频域模型角度分析开环截止频率和相角裕度来设计PI自整定控制器。

综上所述，本文提出了一种改进FCS-MPC系统，利用反馈控制减小电流差拍干扰的作用，所提FCS-MPC实现了较好的控制。为了增强对负载转矩干扰和参数扰动的鲁棒性，进行转速环PI参数的自整定控制方案设计。针对实际系统中的电流约束问题，仿真中设置限幅器对控制系统进行控制，后续可以通过选取较大裕量元器件和结合程序控制中加入电流限制模块实现电流的约束。

1 模型预测优化控制

在传统模型预测电流控制策略中，有近似式为

(1)

在离散化处理时利用式(1)近似处理状态微分方程得到预测模型[11]。因此，虽然模型预测电流控制响应迅速但是受到参数变动的影响比较明显[12]。而基于磁链的FCS-MPC，由于磁链与电流电感的关系也会一定程度地影响响应性能[13]。本文在磁链预测控制的基础上，将输出状态反馈输入到电流预测模型以得到磁链模型对应的k+1时刻电流值，再以此电流作为磁链预测控制的输入，从而使得磁链微分近似式与变化阻感参数相乘得到的k+2时刻预测磁链变化相对平缓，开关矢量输出更加稳定，达到增强稳态性能的效果，构成的控制框图如图1所示。

图1 改进FCS-MPC框图

该方法中，通过将电机电压方程转化为电流的离散模型，再根据电流与磁链的关系进一步得到磁链的离散状态方程:

(2)

将电流模型预测值代入式(2)状态方程进行计算，再选择成本函数为

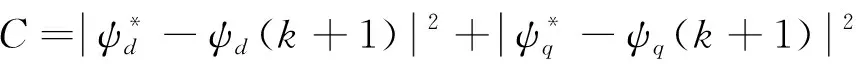
(3)

通过成本函数中磁链的模差值计算可以得到期望的输出状态。计算得到最小成本函数下的开关管状态，使得控制效果达到最好。

2 转速环PI参数自整定

2.1 电机等效模型

分析一个控制系统的数学模型是实现整个控制过程稳定运行的重要基础。而在PMSM闭环控制系统中，分析得到电机速度环的传递函数是至关重要的一个环节。在图1中，可以得到系统的传递函数模型，将整个闭环控制系统按照功能拆分，依次为电机模型、转速环PI控制器、电流电压位置信号采样、FCS-MPC、三相逆变器这5个具体的小模型，通过简化处理得到各自的传递函数。进而得到整个电机闭环控制系统的的等效传递函数。

分析PMSM的电压状态方程，主要由阻感电压和反电动势构成:

(4)

对式(4)进行分析，经过拉普拉斯变换得到频域函数，电机输入三相电压信号，采集输出得到各相的电流信号，从而可以得到该PMSM的等效传递函数为

(5)

式中:L/R为电机时间常数。

式(5)为一个一阶惯性环节，组成整个控制环的一部分。

PI控制器部分可以简化为以下放大环节和积分环节的组合，该速度环的PI控制器等效传函为

(6)

式中:KP、KI为控制器的比例系数和积分系数。

采用的FCS-MPC和逆变器部分可以等效为类似SVPWM的一个一阶惯性环节，主要作用是将经过PI环节处理得到的转矩值经过该环节转换成电机的电压电流值，因此该环节的等效传函为

(7)

式中:K1为改进FCS-MPC的增益系数;Tcf为控制方法的时间常数。

电流电压位置信号采样环节，实现电流到转矩的转换，根据电机机械方程到转速的转变过程，其传递函数为

(8)

式中:J为转动惯量;K2为速度采样的采样系数;K′t为负载转矩系数，K′t=KtTL/TeN；TeN为额定转矩。

整合上文的传递函数得到整个闭环控制系统的等效框图如图2所示。

图2 PMSM转速环系统框图

综合以上各小模型传递函数可以得到电机控制速度环的整个传递函数为

(9)

对该系统传函进行对应的分析，进而为转速环PI参数的自整定做准备。

2.2 抗负载转矩波动的PI自整定

2.2.1 负载转矩辨识

电机在运行过程中，所处的工况不同，除开空载状况外，负载转矩的变化直接影响控制效果，因而速度环PI参数的自整定很大程度上就是基于负载转矩的变化而进行的。因此，进行基于负载波动的速度环PI参数自整定需要构建负载转矩观测器。PMSM机械方程和电磁转矩方程为

(10)

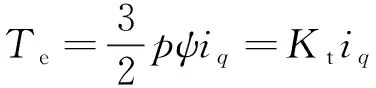
(11)

采用构建观测器的方法进行负载转矩的实时观测[14]，具体分析如下：根据dθ/dt=ωm和式(10)～式(11)分析构建如下观测器:

(12)

观测器的输入变量为机械角位置，状态变量为机械角速度、机械角位置和负载转矩，现只需实时观测电机的负载转矩，简化为

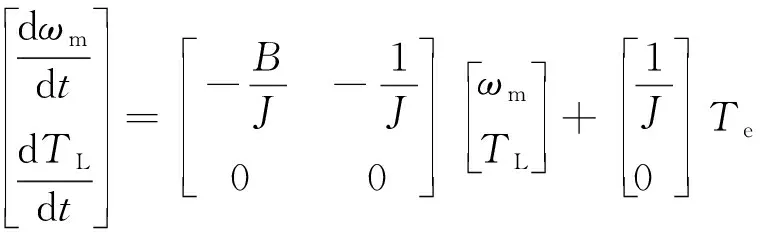
(13)

观测器模型为

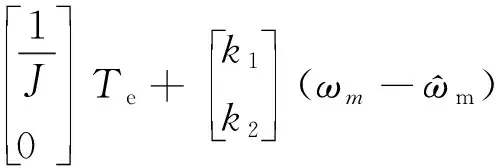
(14)

由式(13)和式(14)可得：

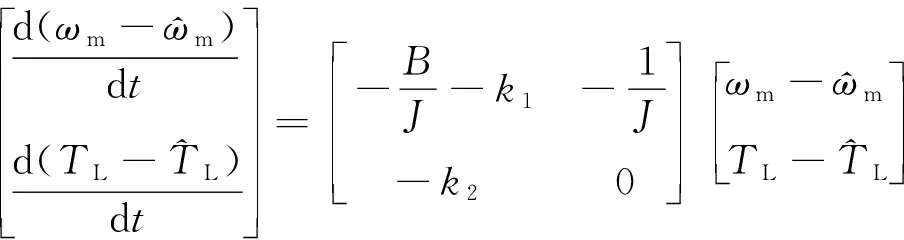
(15)

设系数矩阵为A，则有:

det[sI-A]=s2+(k1+B/J)s-k2/J=0

(16)

选取合适的期望极点α,β,使得系统保持稳定,即:

s2-(α+β)s+αβ=0

(17)

联立式(16)、式(17)求得：

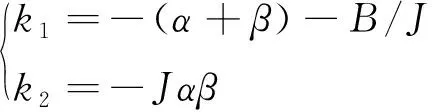
(18)

由以上各式推导可以得到电机状态方程:

(19)

根据状态方程分析，选择极点位置可得负载转矩观测器观测模型如图3所示。

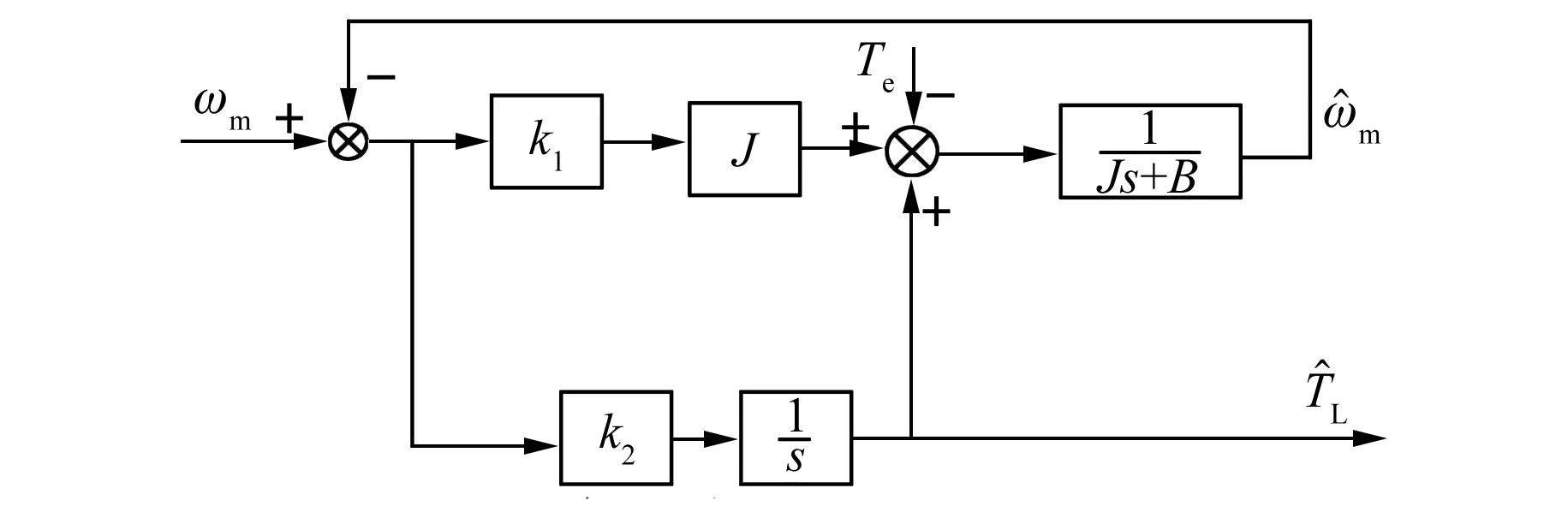
图3 负载转矩观测器框图

2.2.2 频率特性分析法

为了使电机在负载转矩发生突变时仍能够快速的响应工作，需要对该转速环PI参数进行调节。因此,在得到系统的传递函数之后就可以通过频率特性法结合最优控制理论得到PI控制参数与控制稳定性的关系，进一步分析可以到到定量的解析计算式，从而实现完整的自整定控制过程。

(20)

不妨令

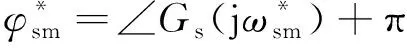
(21)

将式(9)进行整理，分解成调节器环节和其他环节，因为2个惯性环节均是小惯性环节，可以近似合并为一个惯性环节。整理为

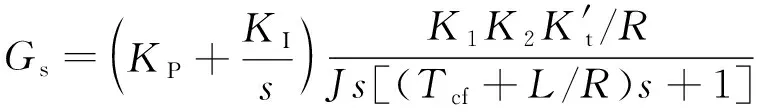
(22)

令

(23)

(24)

(25)

(26)

因而系统传递函数的总幅频特性和相频特性可表示为

(27)

∠Gs=-Qs-phase-Qs-p

(28)

(29)

(30)

通过式(30)便能得到基于模型的参数整定值。当负载转矩发生波动时，可自动调节参数满足幅频和相频特性，使系统具有较好的动态性能。

2.3 抗参数扰动的PI自整定

2.3.1 阻感参数辨识

在负载转矩跟踪控制确定电机控制PI参数大致值确定的情况下，由于电机运行状况以及工作环境的不确定性，电机的阻感参数会随着电机的运行而发生一定的改变，这时需要对电机控制PI参数进行调节使控制效果更加优越。因此文中使用带有遗忘因子的递推最小二乘法进行电机参数的在线辨识[15]。该方法的递推结构表达式为

(31)

式中:θ为待辨识参数矩阵;L为增益矩阵;P为协方差矩阵;λ为遗忘因子。

通过以上递推算法的基本架构，结合PMSM的电压状态方程，得到需要的状态方程:

(32)

式中：θ为需要辨识的部分；y为输出测量部分，y=xTθ；xT为需要的输入量部分。

通过状态方程式(32)，代入递推最小二乘法的迭代式，就可以跟踪到电机的电阻电感参数值，进行后续的控制环节。

2.3.2 典型Ⅱ型系统分析法

为使电机在阻感参数扰动时产生的扰动尽可能小，需要对该转速环PI参数进行调节。因此,在得到了完整的传递函数之后，通过典型系统分析方法得到PI控制参数与系统动态稳定性的关系，进一步分析可以得到定量的控制解析表达式，实现整个完整的自整定控制方案，使得电机的参数鲁棒性提高。

图4为典型Ⅱ型系统的幅频特性图，典型传递函数表示为

图4 典型Ⅱ型系统幅频特性图

(33)

式中:τ和T为时间常数。采用“振荡指标法”中的闭环幅频特性峰值最小准则，可以找到2个时间常数的最佳配合，即τ=hT。

将系统的调节器环节等效转换为

(34)

因而可将整个传递函数式(9)校正成典型Ⅱ型系统的形式为

(35)

K是增益集合，表达式为

(36)

由典型Ⅱ型系统动态抗扰性能指标与参数的关系可知，取h的值为4时动态抗扰性能最佳，参数关系符合最小Mr准则[16]；将系统校正成三阶“最佳”系统，则:

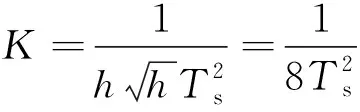
(37)

联立式(36)、式(37)可得：

(38)

由等效转换式(34)可知KI=KP/τ,从而根据该PI整定解析计算式得到需要的整定参数值。

3 仿真分析

3.1 负载转矩变化验证

仿真时给定转速为1 500 r/min，初始负载转矩为10 N·m，t=2 s时负载转矩从10 N·m突变为20 N·m，t=4 s时变为30 N·m，t=6 s时再变为25 N·m，仿真时长为10 s，并调节转速PI到合适值使跟踪较快且无超调。

通过观察仿真图5，在传统矢量控制中，为了保证初始响应的性能，往往设置较小的PI参数值，这样在面对负载转矩突变时会发生抖动且不能快速恢复。图6采用改进的FCS-MPC相对矢量控制在抖动幅度上有一定改善但调节时间还是较长。在转矩观测器下得到的负载转矩变化如图7所示。图8中采用基于负载转矩的频率法转速环PI参数自整定控制，设置和改进FCS-MPC一样的初始控制参数，后续控制参数由整定解析式计算得到，可以看出在转矩发生波动时，转速波动变小且恢复时间短。同时在负载转矩观测模型中，因为转速变化率的影响，所以当转速以一定斜率缓慢变化时，观测到的负载转矩产生了误差，因而需要避免长时间的转速斜坡变换。

图5 负载转矩波动下矢量控制转速响应

图6 负载转矩波动下改进模型预测控制转速响应

图7 负载转矩观测图

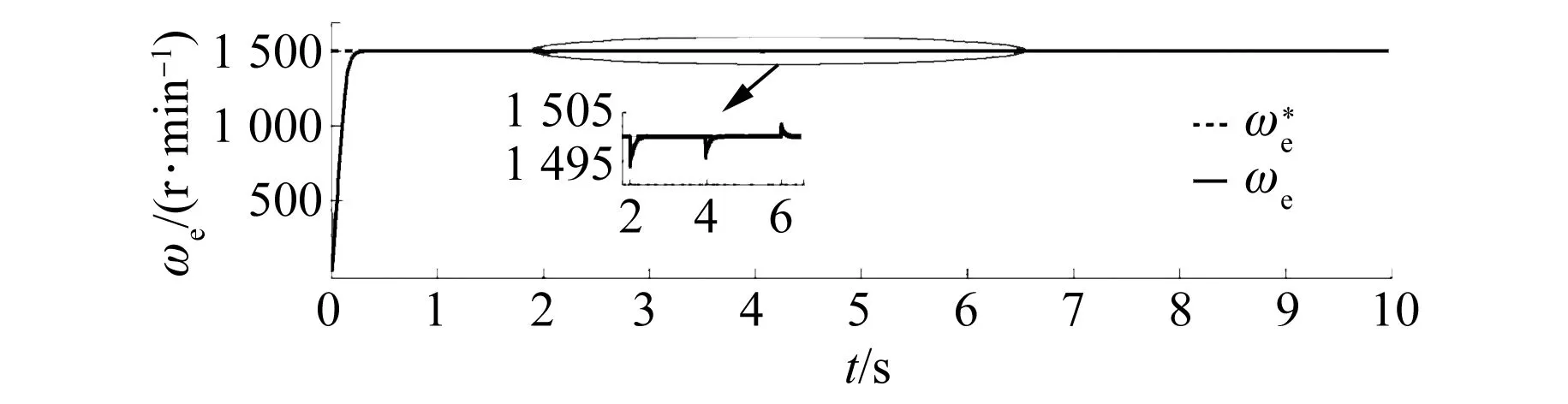
图8 抗转矩波动PI自整定转速图

3.2 参数变化自整定控制验证

仿真时给定转速为1 500 r/min，初始阻感参数分别设置为3 Ω、0.01 H，t=3 s时定子电阻从3 Ω突变为4.5 Ω，t=4 s时电感从0.01 H变为0.015 H，t=5 s时电阻再突变为6 Ω，t=7 s时定子电阻变为4 Ω，t=8 s时电感变化为0.012 H，仿真时长为10 s。

在负载转矩等大扰动验证结束的情况下，对阻感参数扰动进行仿真验证。观察图9可以看出相较于负载波动，阻感参数的扰动使转速波动减小，且方向均与阻感变化方向相反，大小与变化幅度正相关。然后图10中采用改进FCS-MPC，幅度减小，但调节时间依旧较长。基于递推最小二乘法的电机阻感参数辨识结果如图11、图12所示。观察基于典型Ⅱ型系统校正法得到的转速环PI参数自整定控制，如图13所示，因阻感参数扰动引起的转速抖动变得很小且恢复很快，鲁棒性得到明显提升。

图9 参数扰动下矢量控制转速响应

图10 参数扰动下改进模型预测控制转速响应

图11 电阻参数辨识图

图12 电感参数辨识图

图13 抗参数扰动PI自整定转速图

4 结 语

通过对2种电机实际工作中可能遇到的变动工况进行自整定控制方案的仿真验证。当负载转矩发生突变时，采用基于频率法的PI参数自整定控制使整个系统的频率特性带宽和相角裕度保持稳定，能够得到更加优良的响应性能。在针对电机参数的小扰动工况分析中，采用校正为典型Ⅱ型系统的方法进行分析，确定PI自整定控制参数的解析式，同样从仿真结果中可以得知有较明显的效果，验证了理论控制策略的正确性和有效性。