永磁同步电机的改进指数趋近律控制策略

2021-07-20王湘明

电机与控制应用 2021年6期

王湘明，王正

(1.沈阳工业大学信息科学与工程学院，辽宁沈阳 110870；2.沈阳工业大学人工智能学院，辽宁沈阳 110870)

0 引言

永磁同步电机(PMSM)具有结构简单、运行可靠、损耗小、效率高、电机尺寸灵活多样等优点，广泛应用在风机、数控机床、国防等科技领域中[1-2]。由于PMSM是一种非线性、强耦合、多变量、参数时变的复杂系统，使用传统PI调节器，速度调节的品质一般，很难满足高性能的调速要求[3-5]。

为了提高PMSM的调速性能，国内外众多的学者做了大量的研究，如自适应控制[6-8]、模糊控制[9-10]、神经网络控制[11-12]、滑模控制(SMC)[13-17]等。文献[14]提出的二阶滑模算法，减小了开关磁阻电机(SRM)的转矩波纹，消除了抖振现象。文献[15]在双幂次趋近律的基础上，提出三幂次趋近律和一个线性项，可以更快地稳定系统，减小系统的抖动，但该趋近律存在3个幂次项，对控制器的计算能力要求较高。文献[16]根据指数趋近规律，设计的新型趋近律滑模算法，提高了PMSM的动态性能，较大削弱了电机加速和突加负载时的转矩和电流的波动，但趋近律的参数较多。文献[17]设计了一种新型幂次趋近律滑模算法，该趋近律在以往幂次趋近律的基础上通过函数改进和新型函数的引入，实现了系统的快速收敛和无抖振，但算法较为复杂，较难实现。

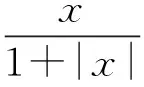
1 PMSM数学模型

为了便于分析与设计，通常选择同步旋转坐标系d-q轴下的数学模型，其定子电压方程可表示为[18]

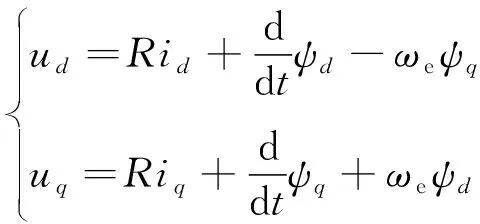
(1)

定子磁链方程为

(2)

由式(1)和式(2)可得定子电压方程为

(3)

式中：ud、uq分别为定子电压的d、q轴分量；id、iq分别为定子电流的d、q轴分量；R为定子的电阻；ψd、ψq为定子磁链的d、q轴分量；ωe为电角速度；Ld、Lq分别是d、q轴电感分量；ψf为永磁体磁链。

电磁转矩方程为

(4)

机械运动方程为

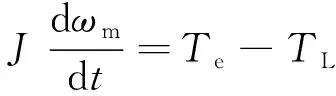
(5)

式中:J为转动惯量；Te为电磁转矩；TL为负载转矩；p为极对数；ωm为机械角速度；

2 改进SMC算法

2.1 趋近律设计

传统的指数趋近律为

(6)

式中：qs为指数趋近项；ksgn(s)为等速趋近项；sgn(s)为符号函数；s为滑模面。

指数趋近律[19]由高为炳院士提出，并在电机控制领域得到广泛的应用。该方法可以在增大q的同时减小k来削弱系统的抖动，由于ksgn(s)等速趋近项的存在，并不能从理论上很好地消除抖动，作为PMSM的速度控制器存在转速超调偏大，鲁棒性不足的问题。

为了更好地解决指数趋近律的抖动和鲁棒性问题，对上述的趋近律进行改进，得到了一种改进趋近律为

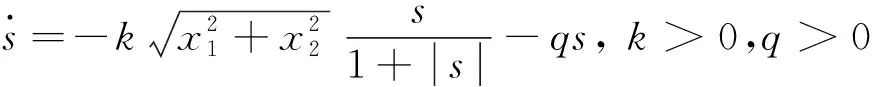
(7)

定义Lyapunov函数如下：

(8)

则有：

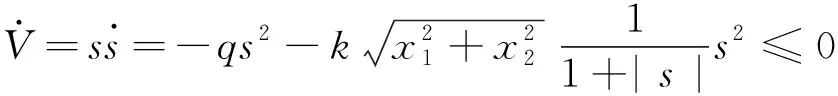
(9)

由式(9)可以看出设计的改进趋近律满足可达性条件[20]。

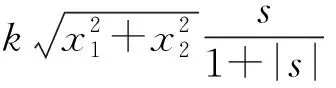
图1 滑模算法的运动阶段

2.2 速度控制器设计

为了简化分析,本文忽略涡流和磁滞损耗；忽略铁心的饱和；永磁体磁场在气隙中为正弦波分布；满足Ld=Lq=Ls，并且采用id=0的转子磁场定向控制策略。定义PMSM控制系统的状态变量为

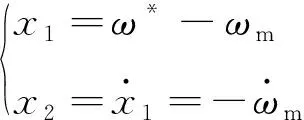
(10)

式中：ω*为给定转速，一般为常数；ωm为实际转速；Ls为定子电感。

由式(4)和id=0可得：

(11)

由式(3)、式(5)和式(11)可得：

(12)

根据式(10)和式(12)可得：

(13)

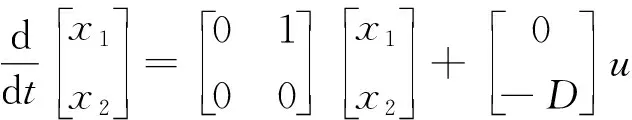
(14)

定义滑模面函数为s=cx1+x2,c>0,对其求导可得：

(15)

根据式(7)和式(15)得：

(16)

从而得到q轴的参考电流

(17)

由式(17)可以看出，由于控制器包含有积分项，可以在消除系统稳态误差的同时削弱系统的抖动现象，提高PMSM速度控制的品质。

3 仿真分析

为了验证本文所提改进趋近律的可行性，设计了PMSM双闭环调速系统，如图2所示，其中电流环的控制器采用传统的PI控制，速度环的控制器采用改进SMC；同时建立了MATLAB/Simulink仿真模型，并与传统的PI控制器、指数趋近律SMC进行比较。

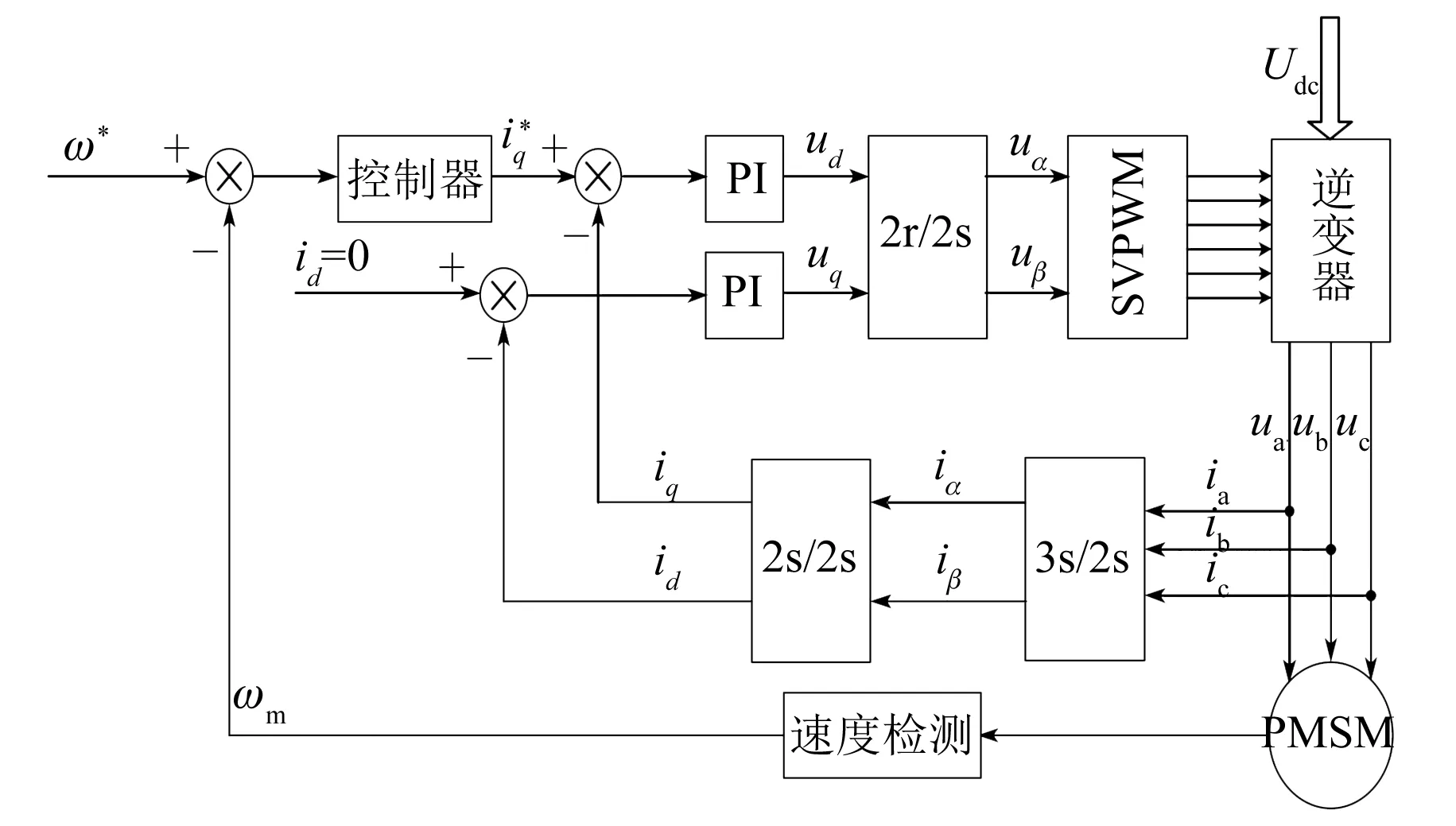
图2 调速系统框图

仿真时电机所用的参数如表1所示[21]。改进趋近律滑模速度控制器参数设置为,c=45,q=300,k=1 050;仿真条件为,电机的给定转速ω*=1 500 r/min，初始的负载转矩TL=0 N·m,在t=0.3 s时突加负载TL=10 N·m,仿真时间为0.6 s。

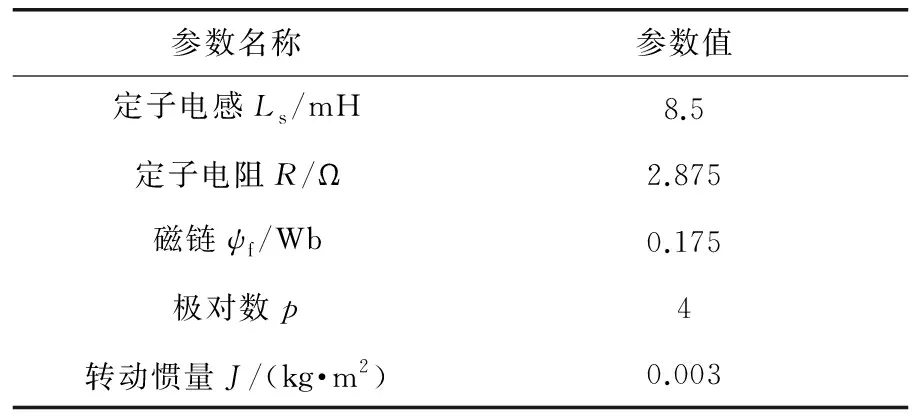
表1 PMSM参数

图3可以看出，当系统在0.3 s加入负载时，系统的状态变量收敛时间需要约0.268 s。图4中分别为PI控制器、传统的指数趋近律SMC和改进趋近律SMC下的转速响应曲线。从图4可以看出，传统指数趋近律SMC的超调最大，PI控制器的超调次之，改进趋近律SMC的超调最小。图5可以看出，在PMSM突加负载时，PI控制器和传统指数趋近律SMC的转速波动超过了约75 r/min，且转速波动较大，而改进趋近律的SMC转速波动约25 r/min，转速的波动小。

图3 改进滑模系统状态变量收敛时间

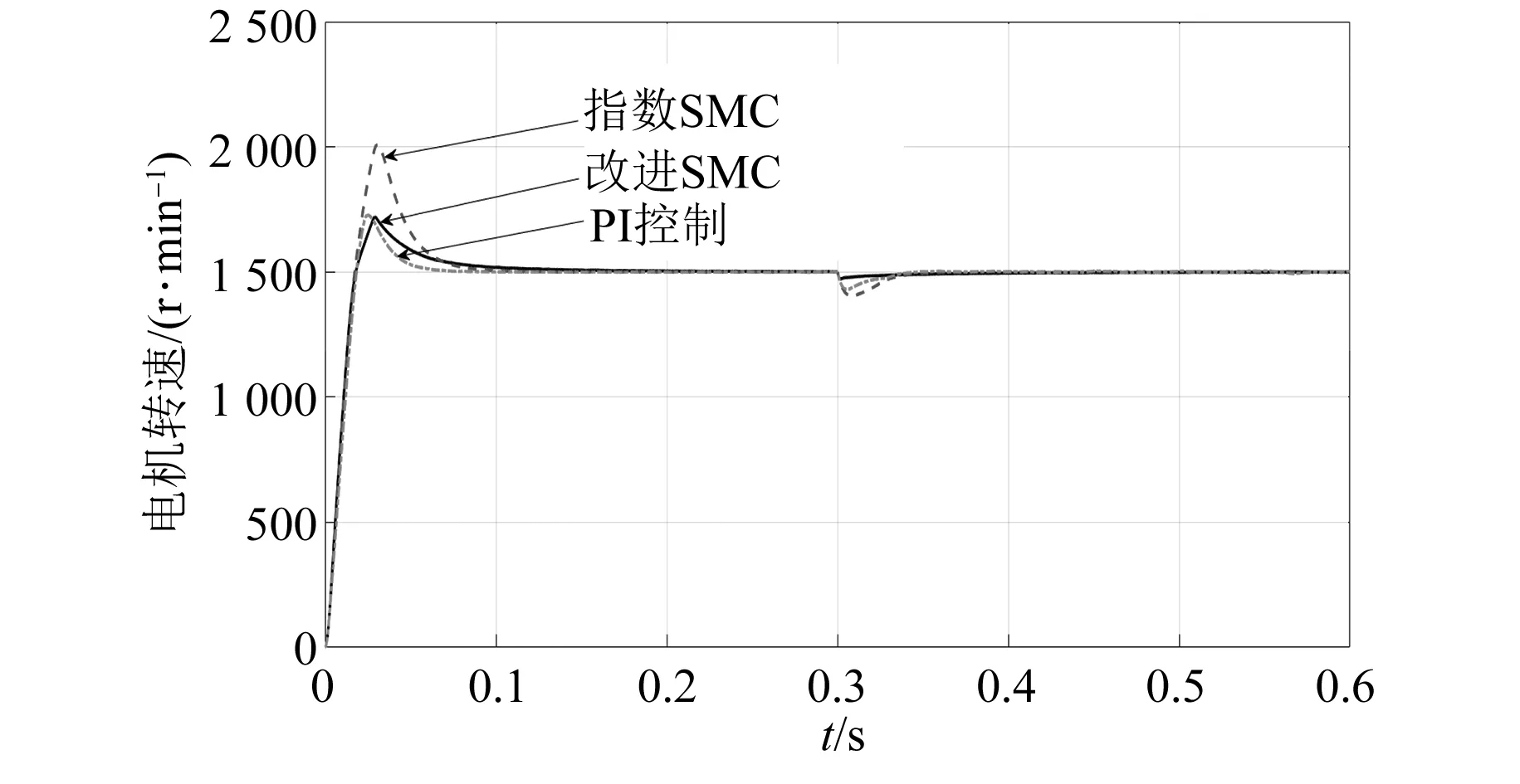
图4 转速曲线

图5 突加负载的转速曲线

图6结果表明，在PMSM起动的过程中，电磁转矩在改进趋近律SMC作用下快速地到达稳态，在0.3 s时突加负载时，改进趋近律SMC能在0.004 s左右使转矩趋于平稳，而传统的指数趋近律SMC和PI控制器需用更多的时间使转矩趋于平稳。

图6 电磁转矩曲线

当电机的负载在0.3 s变化时，由图7可以看出使用PI控制器时，大约在0.305 s电流第一次到达10 A，由图8可以看出使用传统指数SMC时，电流大约在0.307 s第一次到达10 A，图9表明采用改进趋近律SMC时，电流大约在0.302 s第一次到达10 A；在加入负载的0.05 s内使用传统指数SMC的电流变化最大，使用PI控制器的电流变化次之，使用改进趋近律SMC的电流变化最小。