改进的永磁同步电机双矢量模型预测转矩控制*

刘述喜， 孙超俊， 杜文睿， 程楠格

(1.重庆理工大学 电气与电子工程学院，重庆 400054；2.重庆市能源互联网工程技术研究中心，重庆 400054)

0 引 言

永磁同步电机(PMSM)具有结构简单、高效率、高功率密度和可靠运行等特点，广泛应用于多个领域[1]。当前PMSM控制方法主要有矢量控制和直接转矩控制。虽然矢量控制得到广泛应用，但动态响应较差，且严重依赖参数整定。直接转矩控制结构简单，可实现快速动态响应，但仍存在转矩脉动过大，开关频率不固定的问题[2]。模型预测转矩控制(MPTC)凭借其控制结构简单，容易实施，动态响应快速的优势，吸引了众多学者对其深入研究[3]。

传统的MPTC通过逆变器产生开关状态，并利用有限开关状态所代表的电压矢量去预测下一时刻的转矩和磁链，将代价函数作为预测值的评价标准，选取使代价函数最小的电压矢量作为最优矢量作用于电机[4]。该方法在一个周期内只有一个电压矢量作用，并且变换器只产生7个电压矢量，转矩纹波依然较大。文献[5]提出了占空比MPTC，将传统MPTC采样周期分为2段时间，有效电压矢量作用一段时间，其余时间由零矢量代替，从而减小转矩纹波。文献[6]提出了一种改进占空比MPTC方法，通过将矢量选择和作用时间并行优化，在减小采样频率的同时获得更好的低速性能。

以上方法虽然对系统性能进行优化，但是均需以电磁转矩和定子磁链为控制变量。代价函数通常由转矩误差和定子磁链误差2个分量组成，由于两者具有不同的量纲，难以通过设计权重系数平衡代价函数中转矩和磁链的控制性能。目前权重系数的设计缺少扎实的理论基础，需要庞杂的仿真和实验得出[7]。文献[8]提出转矩脉动最小化原理优化计算权重系数的方法。该方法有所优化，但其计算公式复杂，计算难度过大。文献[9]提出将磁链和转矩之间权重系数的整定调整为定子磁链控制。但该方法设计过程复杂，实施困难。

针对传统MPTC权重系数整定复杂和转矩脉动问题，以内置式永磁同步电机(IPMSM)为例，提出了一种改进的IPMSM双矢量MPTC。依托6个有效虚拟矢量来增加候选矢量，转矩和磁链经过转矩电压矢量作用产生，减小候选矢量数量，从而减小计算量。以无差拍转矩控制和无差拍磁链控制为基础，选择对应占空比优化方式。比较两者占空比优化值，根据所提优化策略找寻最优矢量，从而解决了转矩和磁链所占比重的权重系数难以整定的问题。最后利用MATLAB/Simulink进行验证，仿真结果表明所提改进方法与传统MPTC相比，不仅能提高稳态性能，而且能保留MPTC动态性能优越的特点。

1 IPMSM的数学模型

IPMSM因其永磁体嵌入转子内，与表贴式电机相比，功率密度和动态性能有所提高。构建IPMSMd-q坐标系下数学模型[10]，其中d-q轴电压方程为

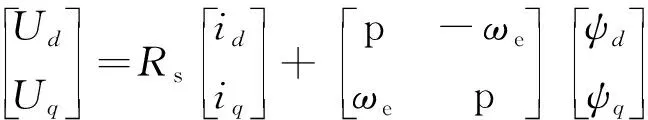
(1)

式中：Ud、Uq为电机定子电压的d、q轴分量；ψd、ψq为电机定子磁链的d、q轴分量；Rs为电机的定子相电阻；p为微分算子。

并且有：

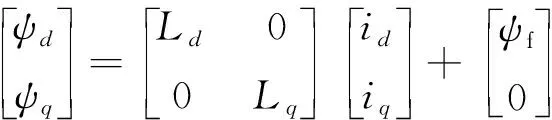
(2)

式中：Ld、Lq分别为电机的d、q轴电感；ψf为电机的永磁体磁链。

电磁转矩可表示为

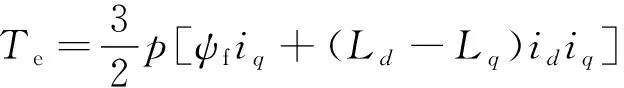
(3)

式中：p为永磁同步电机的极对数。

2 传统MPTC策略

2.1 传统MPTC原理

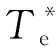
图1 传统MPTC的原理框图

2.2 控制延时补偿

由式(3)可以看出，电磁转矩Te的预测是基于当前时刻(k时刻)的电流is(k)，但由于数字控制系统存在一拍延迟[11]，所选择的最优矢量要到下一时刻(k+1时刻)才会被输出。从而导致逆变器应用上一时刻开关状态，增加转矩和磁链脉动。因此，需要以k+1时刻的变量作为初始值对k+2时刻的变量进行预测，从而消除一拍延迟影响。

将式(1)所示的电机数学模型运用前向欧拉法将其离散化，可得：

ωe(k)Lqiq(k)+Ud(k)]Ts

(4)

ωe(k)Ldid(k)-ωe(k)ψf+Uq(k)]Ts

(5)

式中：Ts为系统控制周期;Ud(k)、Uq(k)分别为k时刻采样电压值U(k)所对应的d、q分量。

由式(4)、式(5)可知，利用k时刻的采样电流is(k)和输出的电压矢量代入式(4)、式(5)预测出k+1的电流值。将is(k+1)代入式(2)、式(3)得到k+1时刻转矩Te(k+1)和磁链ψs(k+1)，以k+1时刻变量作为初值对k+2时刻变量预测。

2.3 最优矢量选择

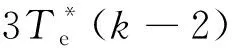
(6)

(7)

并将经过延时补偿之后得到的k+1时刻转矩和磁链初值代入预测方程求出k+2时刻变量，将其代入代价函数式(8)中。找寻最小代价函数所对应的电压矢量作为最优矢量。

(8)

3 改进的双矢量MPTC策略

为了减小传统MPTC转矩和磁链脉动，添加虚拟电压矢量。建立定子磁链定向的旋转坐标系，并将其划分为4个扇区，通过确定扇区来缩小候选电压矢量的范围。利用备选矢量的转矩占空比和磁链占空比，构建新的寻优规则，代替代价函数，避免权重系数整定。结果表明，候选电压矢量和计算量减少。

3.1 虚拟矢量和旋转扇区

传统MPTC将电压矢量空间划分为6个扇区，并包含6个有效电压矢量和2个零矢量。将其中6个有效电压矢量u1、u2、u3、u4、u5、u6作为最基本矢量。基本矢量空间分布如图2所示。

图2 基本矢量空间分布图

虚拟电压矢量通过相邻2个基本矢量进行合成，从而使候选矢量变为12个。新增矢量分别表示为u7、u8、u9、u10、u11、u12。将电压矢量扇区平均分为4个小扇区，每个扇区均为90°，且均包含3个候选矢量。电压矢量扇区和候选矢量划分如图3所示。

图3 电压矢量扇区和候选矢量划分图

图4所示为定子电压矢量作用图，将式(2)进一步表示为[12]

(9)

式中：ψs为定子磁链；δsf为负载角，其由定子磁链矢量ψs和永磁体磁链矢量ψf得出。

将式(2)和式(9)代入式(3)得：

(10)

式(10)表明，若定子磁链ψs不变，则转矩仅与负载角δsf有关，改变负载角δsf即可改变电磁转矩Te。由于负载角δsf增量表示为

综上所述，建设数字城市基础地理信息系统数据库有助于推动“数字城市”建设的推进，可有效促进信息化城市建设进程。基于此，本文以数字城市基础地理信息系统数据库为研究对象，从多源数据的标准化与规范化，城市空间数据的转换，元数据的处理，数据的存储、管理、动态更新与维护、共享与数据安全等7个方面分析了建设数字城市基础地理信息系统数据库的要点，本文的研究成果将对推动数字城市基础地理信息系统数据库建设提供一定的参考价值。

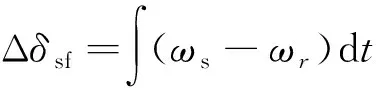
(11)

式中：Δδsf为负载角增量；ωs为定子磁链旋转速度。

根据式(11)可知，通过改变ωs和ωr的大小即可改变负载角增量Δδsf，从而进一步改变电磁转矩Te。根据图4可知，每个候选矢量un可分解为径向分量usr和切向分量usn，其表达式为

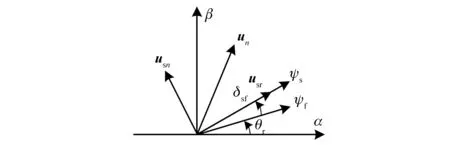
图4 候选矢量Un坐标分解图

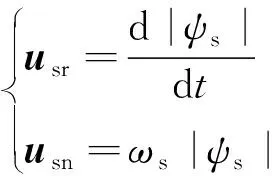
(12)

式(12)中，径向分量usr保持定子磁链ψs相位不变，切向分量usn保持定子磁链ψs幅值不变。控制径向分量usr可以改变定子磁链ψs大小，控制切向分量usn可以改变定子磁链ψs的转速ωs。

故根据定子电压矢量与定子磁链矢量轨迹变化原理，转矩和磁链可由扇区1中矢量作用而同时增大；由扇区3中矢量作用而同时减小；由扇区2中矢量作用增大转矩，减小磁链；由扇区4中矢量作用减小转矩，增大磁链。

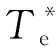
表1 扇区选择规则表

确定扇区位置后，可通过磁链位置角选择候选矢量。以1号扇区为例，其电压矢量选择表如表2所示。

表2 候选矢量表

3.2 传统占空比计算

文献[6]提出传统占空比计算。首先通过价值函数选择最优矢量，该最优矢量使转矩和磁链误差和在下一个控制周期最小。其中，矢量占空比根据转矩误差计算。然后，通过将占空比与模型预测控制结合，优化一个周期内单个电压矢量作用引起的转矩和磁链脉动。然而此方法在2种情况下不能很好起作用：(1)与转矩和磁通相对应的矢量占空比之间的差值过大，以至于无法通过调节占空比来平衡转矩和磁链的控制性能；(2)当占空比为1时，最优矢量可以获得最佳控制性能，此时占空比调节无调节作用，转矩和磁通没有达到参考值。本文考虑了占空比计算和最优矢量选择，以解决上述问题。

在一个控制周期中，转矩和磁链的变化量被表示为ΔT和Δψ。在零电压矢量的作用下，转矩和磁链的变化近似为0。当转矩误差为0，相应矢量的占空比也为0。因此，转矩和磁链在一个控制周期结束后可以表示为

(13)

转矩和磁链的占空比可以表示为

(14)

转矩变化量ΔT和磁链变化量Δψ可以表示为

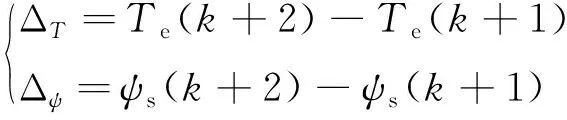
(15)

式中：Te(k+1)和ψs(k+1)为加入延迟补偿后k+1时刻的转矩和磁通，并通过式(1)～式(5)可以预测k+2时刻的转矩Te(k+2)和磁通ψs(k+2)。

3.3 最优矢量选择

如图3和表2所示，3个候选矢量由所在扇区决定。3个候选矢量的转矩和磁链变化量分别表示为ΔT1，ΔT2，ΔT3和Δψ1，Δψ2，Δψ3。转矩占空比DT1，DT2，DT3和磁链占空比Dψ1，Dψ2，Dψ3由式(14)计算得出，且数值被限幅在0～1之间。当主要控制目标为转矩时，由占空比确定的最优矢量选择规则如下：

规则1：当DT1=DT2=DT3=1时，即等于没有加入占空比环节，3个矢量均不能使转矩在一个控制周期内达到参考值。此时，令转矩变化量最大的电压矢量作为最优矢量，同时占空比为1。

规则2：当DT1，DT2，DT3其中一个<1时，相应的矢量可以使转矩达到参考值。则选择该矢量作为最优矢量，其转矩占空比为最优矢量占空比。

规则3：当DT1，DT2，DT33者均<1时，这表明3个矢量均可以让转矩达到参考值。此时选择3个矢量中磁链和转矩占空比差值最小的矢量作为最优电压矢量，其对应的转矩占空比作为最优占空比。

规则4：当DT1，DT2，DT3其中2个<1时，即这2个矢量均可以使得转矩达到参考值。此时最优矢量的选择同规则3。

具体规则如表3所示。umin(1_2)是在2个候选矢量1和矢量2作用下转矩和磁链占空比差值最小的电压矢量。DTmin为其差值最小所对应占空比，umax(ΔT)转矩变化值最大情况下的电压矢量，umin(1_2_3)是3个候选矢量作用下转矩和磁链占空比差值最小的电压矢量。

表3 最优矢量选择规则表

本文所提出的改进的双矢量MPTC方法的流程框图如图5所示。

图5 改进的双矢量MPTC控制方法的流程框图

通过对电压矢量选择的优化，转矩的控制能力已经被改进，并且可以在一定程度上考虑磁链控制性能。该系统的控制图如图6所示。

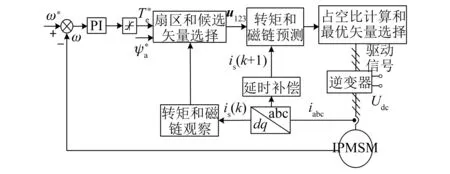
图6 改进的双矢量MPTC图

4 仿真结果与分析

在MATLAB/Simulink中搭建相应的仿真模型，对提出改进的双矢量MPTC的可行性进行验证。将传统占空比MPTC和本文所提改进的双矢量MPTC分别称为MPTC-I，MPTC-II。仿真中所用电机参数如表4所示。

表4 IPMSM参数

为验证本文所提出改进方法对转矩和磁链控制性能的改进，对以上2种方法进行稳态和动态性能仿真。图7(a)、图7(b)所示分别为MPTC-I和MPTC-II 2种策略的满载工况下转矩、定子磁链、单相电流仿真波形。仿真中，IPMSM的转速设定为3 000 r/min，转矩设定为55 N·m，采样频率为10 kHz。

图7 稳态仿真波形对比

通过比对图7(a)和图7(b)可以看出，本文中所提出的双矢量MPTC策略下的转矩脉动明显低于传统占空比控制策略，定子磁链波形更加稳定，单相电流波形更加平滑。

图8(a)、图8(b)所示分别为MPTC-I和MPTC-II2种控制策略在1 s时突加负载的转矩、定子磁链和单相电流仿真波形。电机从0 r/min加速到额定转速3 540 r/min，在1 s时将额定负载55 N·m加载到电机。

图8 动态仿真波形对比

通过比对图8(a)和图8(b)可以看出，电机在2种方法下均能稳定起动，转矩和磁链可以快速跟踪参考值。在加载额定负载55 N·m之后，电机能够快速达到稳定状态，说明系统拥有良好的抗扰动能力。但是在MPTC-I中转矩和磁链的扰动要大于MPTC-II。原因是在MPTC-I中占空比大多数时间为1。由图9可以看出，当占空比为1时，代价函数判断出的最优矢量并非理想矢量，转矩或磁链无法快速跟随，占空比会达到极限。而MPTC-II中所采用的矢量可能不一定为最优矢量，但是由于占空比调节的存在，其占空比在0～1之间改变，转矩和磁链可以很好地跟踪参考值。所提MPTC-II在动态性能不变的同时，转矩和磁链控制性能均得到改善。

图9 占空比仿真波形对比

5 结 语

本文提出了一种改进的双矢量MPTC方法。该方法引入了虚拟矢量，建立了旋转坐标系，运用转矩占空比和磁链占空比的逻辑关系取代传统代价函数判定最优矢量，避免了权重系数整定的问题。与方法MPTC-I所比较，所提方法充分利用了占空比调节功能，具有良好的转矩和磁链控制性能。仿真结果表明，所提MPTC-II是有效的。