一类分数阶薛定谔方程的驻波解
2021-07-20路慧芹
路慧芹 张 悦
( 山东师范大学数学与统计学院, 250358, 济南 )
1 引 言
分数阶薛定谔方程由于其深刻的物理背景和重要的应用价值而受到广泛关注,已成为分数阶微分方程研究领域的一个新热点.Laskin N利用Lévy型路径上的积分建立起来的分数阶量子力学模型是如下形式的分数阶薛定谔方程[2]
i∂tψ=(-Δ)αψ+V(x)ψ-|ψ|p-2ψ, ∀(t,x)∈×N,
(1)
其中i是虚单位,0<α<1,V(x)是势函数,ψ是反映粒子在势场中运动情况的波函数.
令u(x)是下述方程
ωu=(-Δ)αu+V(x)u-|u|p-2u, ∀x∈N
(2)
的解,其中ω>0,则ψ=e-iωtu(x)是方程(1)的一个驻波解.

众所周知,若V(x)满足下列条件:
(V)V∈C(N,且存在r0>0 使得对任意的M>0当|y|→∞时都有
meas({x∈Br0(y):V(x)≤M})→0,
则算子(-Δ)α+V(x)有一串特征值0<λ1<λ2≤…≤λm≤λm+1≤…,λm→∞(m→∞),且每个特征值的重数都是有限的.
本文的目的是研究频率ω>λ1时方程(1)的非平凡驻波解的存在性,利用环绕定理证明当ω≠λk(k=1,2,…)时方程(1)具有一个非平凡的驻波解,从而推广和补充文献[1]的结果.
2 预备知识和引理
方程(1)中的分数阶拉普拉斯算子(-Δ)α定义为:(-Δ)αu:=I-1(|ξ|2α(Iu)), 其中I是傅里叶变换.
文中使用Hα(N)的子空间
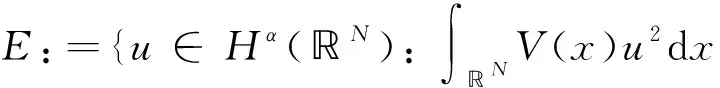
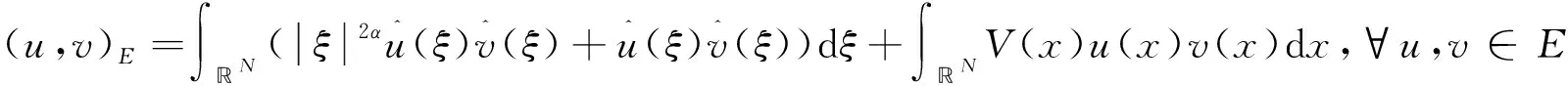
下是Hilbert空间. 在条件(V)下,內积(u,v)E导出的范数‖·‖E等价于下述范数
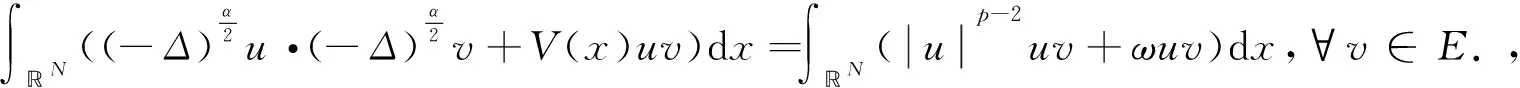
(3)
显然,Jω(u)∈C1(E,) 且
(4)
引理1设N>2α, 2 证令{un}⊂E是一个(C)c序列,即 (5) 需证{un}有一个收敛子列. 由(5)式知 (6) 可以断言{un}是有界的,若否,则当n→∞时有‖un‖→∞.由(3)式,(4)式和(6式)可得 其中‖·‖p是Lp(N)中的范数. 由于2 由(4)式和(6)式可得 (7) 由于‖un‖p是有界的,故对上式取极限得 (8) 下证φ≡0.假设φ≡0, 在(7)式中取v=φn,可得 在上式两端同除以‖un‖,并注意到‖un‖p是有界的,可得 (9) 由紧嵌入定理[6]可知在L2(N)中φn→0. 于是由(9)式知 ‖φn‖→0, 与‖φn‖=1矛盾. 于是E中的非零函数φ满足(8)式,即ω是算子(-Δ)α+V(x)的一个特征值,此与题设条件矛盾. 由此可见,{un}是有界的. 因此{un}在E中存在弱收敛子列,不妨仍记为{un}在E中弱收敛于u. 于是由紧嵌入定理和赫尔德不等式易知即在E中un→u. 定理1若N>2α, 2 证对任意满足ω≠λk(k=1,2,…)的正数ω,必存在非负整数m,使得ω∈(λm,λm+1). 若m=0,即ω∈(0,λ1)时,文献[3]利用Nehari流形方法得到了方程(1)具有一个非平凡的驻波解. 下面证明当ω∈(λm,λm+1),m∈时定理的结论也成立. V=span{e1,e2,…,em},X={u∈E:(u,ei)=0,∀i=1,2,…,m},W=V⊕span{em+1}, (10) 显然V,W都是E的有限维子空间且E=V⊕X. 令u∈X, 则由嵌入定理可得 (11) 由于p>2且ω<λm+1, 因此由(11)式知,存在充分小的正数ρ和β,使得Jω|∂Bρ∩X≥β. 令u∈W, 由于ω>0以及有限维Banach空间的所有范数等价,可知存在常数κ>0,使得 (12) 由于p>2, 因此由(12)式知,存在正数R>ρ,使得Jω(u)≤0,∀u∈W,‖u‖≥R.令 易知Q⊂W, 进而有Jω|∂Q≤0. 综上所述,由引理1和环绕定理[7]可知定理1的结论成立.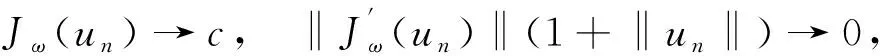
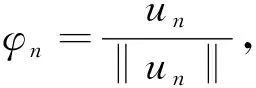
3 主要结果