限制线性模型和转换线性模型参数估计的等价性

崔文婧 赵 强

( 山东师范大学数学与统计学院,250358,济南 )

1 引 言

线性模型是现代统计学中理论丰富、应用广泛的一个重要分支,在现代统计学中占据着十分重要的地位.线性模型是一类统计模型的总称,它包括了线性回归模型,方差分析模型和协方差分析模型等.生物、医学、经济和工程技术等众多领域的现象均可以通过线性模型来近似的描述,所以线性模型是现代统计学中应用最为广泛的模型之一.对于线性模型的研究吸引了许多学者的关注.在实际问题中对模型的分析少不了对参数进行估计,因此对参数估计的研究显得尤为重要,关于参数估计许多学者已经做了大量研究.在线性模型参数估计中最小二乘估计(OLSE)有着重要地位,而最佳线性无偏估计(BLUE)也是应用非常广泛的参数估计之一.对于一般线性模型M={y,Xβ,∑},OLSE,BLUE是关于参数函数Kβ最常用的两个估计,因此研究两者之间关系是有意义的.

下面讨论限制线性模型和转换线性模型下,参数函数Kβ的OLSE和BLUE之间的关系.限制线性模型记为

Mr={y,Xβ|Aβ=b,∑},

(1)

其中y是n×1阶可观测的随机向量,X是n×p阶任意秩的已知矩阵,A是m×p阶的已知矩阵,b是m×1阶的已知向量,β是p×1阶可估的参数向量,∑是已知或未知的n×n阶任意秩的对称非负定矩阵.转换线性模型记为

Mt={By,BXβ,B∑B'},

(2)

其中B是m×n阶任意秩的给定矩阵.

本文将利用矩阵广义逆的表达式和矩阵秩公式,对限制线性模型(1)和转换线性模型(2)下，参数函数Kβ的OLSE和BLUE之间相等关系成立的等价条件进行研究,给出参数函数Kβ在不同模型下同一参数估计相等关系成立的等价条件.本文的结构如下:第一部分介绍研究背景和研究现状;第二部分给出证明需要的相关定义、引理等准备知识;第三部分给出在(1)式和(2)式下的参数函数Kβ的OLSE和BLUE相等的等价条件以及相应的证明过程.

2 预备知识

在本文中Rm×n表示所有的m×n阶实矩阵,假设矩阵M∈Rm×n,用符号M',r(M),R(M)分别表示矩阵M的转置、秩和列空间.

定义1[1]设矩阵M∈Rm×n,若矩阵G满足如下四个方程:

1)MGM=M；

2)GMG=G；

3) (MG)'=MG；

4)(GM)'=GM；

则矩阵G称为矩阵M的Moore-Penrose广义逆,简称为M的M-P逆,记为M+.有时称上述四个方程为Penrose方程.令PM,EM和FM分别表示三个正交投影阵,其中PM=MM+,EM=Im-MM+,FM=In-M+M.

定义2[2,3]若y∈R[X,∑],则称一般线性模型M={y,Xβ,∑}是一致的.

为了研究模型(1)和(2)下估计量的关系,假设两个模型均是一致的.

定义3[4]设K是给定的q×p阶矩阵,参数函数Kβ在一般线性模型M下可估,当且仅当R(K')⊆R(X')成立.

由定义3知当且仅当R(K')∈R[X',A']成立时,参数函数Kβ在(1)式下可估;当且仅当R(K')⊆R(BX')成立时,参数函数Kβ在(2)式下可估[5].

引理1[6,7]假设Kβ在Mr和Mt下均是可估的,则Kβ在Mr和Mt下的OLSE可写成如下参数形式:

(3)

OLSEMt(Kβ)=K(BX)+By,

(4)

其中KA=KFA,XA=XFA.

引理2[6,8]假设Kβ在Mr和Mt下均是可估的,则Kβ在Mr和Mt下的BLUE可写成如下参数形式:

BLUEMr(Kβ)=(I-PKA;XA;∑)XA+b+PKA;XA;∑y,

(5)

其中KA=KFA,XA=XFA,PKA;XA;∑=[KA,0][XA,∑EXA]++UE[XA,∑EXA],U是q×n阶的任意矩阵；

BLUEMt(Kβ)=PK;BX;B∑B'By,

(6)

其中PK;BX;B∑B'=[K,0][BX,B∑B'EBX]++VE[BX,B∑B'EBX],V是k×q阶的任意矩阵.

引理3[8]设A∈Rm×n,B∈Rm×k,C∈Rq×k,D∈Rq×k,则下述结论成立：

1)r[A,B]=r(A)+r(EAB)=r(B)+r(EBA)；

6)r[A,B]=r(A)⟺EAB=0⟺R(B)⊆R(A).

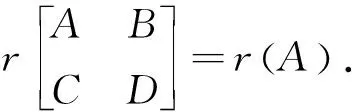
众所周知,当且仅当矩阵A的秩为零时,矩阵A是零矩阵.由此可知对于两个同阶矩阵A和B,当且仅当r(A-B)=0时有矩阵A和B相等.如果能推导出r(A-B)的相关公式,就可以以此来刻画两个矩阵之间的关系.因此研究同阶的两个矩阵关系的一个简单且有效的方法是考虑两个矩阵差的秩,这种代数方法称为矩阵秩法.Tian Y等人[9,10]利用矩阵秩方法刻画了一般线性模型M下估计量的各种等式.在本文中,将使用这种方法来研究在Mr和Mt下参数函数Kβ的OLSE和BLUE的等价性.

3 参数函数的估计量之间的关系

引理4[6]假设一般线性模型M是一致的,L1y+c1和L2y+c2为Kβ在M下的两个无偏估计,即E(L1y+c1)=E(L2y+c2)=Kβ，则当且仅当L1∑=L2∑时,有等式L1y+c1=L2y+c2L2y成立.

定理1假设Kβ在Mt下可估,OLSEMr(Kβ)和OLSEMt(Kβ)如(3)式与(4)式所示,则

1) 下列结论等价:

①OLSEMr(Kβ)=OLSEMt(Kβ)；

2) 若∑是正定的,下列结论等价:

①OLSEMr(Kβ)=OLSEMt(Kβ);

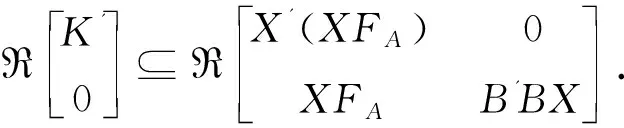
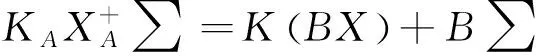
下面证明1)中的结论②等价于结论③.利用引理3中的结论5)和初等矩阵分块运算,可得

所以当且仅当

(7)

成立时,1)中的结论②也成立,而由引理3的结论6)可知(7)式等价于1)中的结论③,则结论②和结论③的等价性得证.

下面再考虑定理中2)的情况.当∑是正定的,此时可对(7)式简化得到

由引理3的结论6)可知上式等价于2)中的结论②,同理2)中的结论①和结论②等价.因此定理1得证.

定理2假设Kβ在Mt下可估,BLUEMr(Kβ)和BLUEMt(Kβ)如(5)式与(6)式所示,则下列结论等价:

1)BLUEMr(Kβ)=BLUEMt(Kβ)；

证由引理4可知,当且仅当PKA;XA;∑∑=PK;BX;B∑B'B∑时，有BLUEMr(Kβ)=BLUEMt(Kβ).利用引理3中的结论2) 和初等矩阵分块运算,可得

r(PKA;XA;∑∑-PK;BX;B∑B'B∑)

因为EXFA=F(XFA)',EBX=F(BX)',由引理3的结论2)可知

由引理3的结论2)可知

所以

r(PKA;XA;∑∑-PK;BX;B∑B'B∑)

令(8)式右边等于0可知定理2中的结论1)和结论2)是等价的,即当且仅当

(8)

成立时定理2中的结论1)和2)是等价的.由(9)式可知定理2中的结论2)和结论3)是等价的,因此定理2得证.