试析化归思想在数学教学中的应用

夏 婵

(广东省湛江市第七中学 广东 湛江 524000)

初中数学具有一定的抽象性，和其他的学科有所不同，如果单纯的照本宣科的讲解，学生理解是有着一定的困难的，教师在教学之中要寻找相关的数学规律，融入数学思想，帮助学生找到解决问题的办法。化归思想作为一种重要的数学思想，可以促进学生的思考，将知识化繁为简，帮助学生树立学习的自信，提升学生的数学水平。

1.化归思想的含义

在初中数学的学习中，涉及到了很多的数学思想，其中就包括了化归思想、数形结合思想等。在数学教学中化归思想是教师运用最多的思想方法，学生只有熟练地运用数学思维才能够有高效简便的解题思路解决数学问题，从而提升学生的数学能力。化归思想从字面上就能够看出它的含义，就是转化和归纳的过程，将复杂的问题变得简单。运用化归思想，学生可以利用已经掌握的知识，将待解决的问题转化为比较简单的问题，在初中数学之中每一个数学问题都是通过不断的转化解决的，无论是数形结合还是函数方程都是化归思想的一种表现形式。如果能够将化归思想运用到初中数学的教学之中，将有助于化繁为简，将难以理解的知识点转化成一般的知识点，帮助学生进行理解。

2.化归思想在初中数学中的应用策略

2.1 运用化归思想进行新知识的学习。在数学的学习之中，通过长期的研究和实践，我们总结了大量的理论知识，也丰富了很多的实际经验，对于共性的问题形成了固定的解决步骤和方法。对于有着固定的解决方法和步骤的问题，人们把他视为规范问题，将一个陌生的或者是复杂的问题，转化为规范性的问题的过程称为化归[1]。例如，在学习一元二次方程的时候，学生已经学习了有关求根的方法和相关的理论，在进行一元二次方程解题的过程当中更多的是规范化的问题。将无理方程、分式方程通过化归的方式转化为一元二次方程的过程就是问题的规范化的过程。就如同在解一元三次方程的时候，可以利用划归思想将一元三次方程转化为一元一次方程，从而使问题变得更加简单。如：已知：χ2+ χ-1=0,求χ3+2χ2+2009的值。可以将其降次转化，从而降低解题难度，解法：原式=χ(χ2+ χ-1)+(χ2+ χ-1)+2010=2010。

2.2 运用化归思想提升学生思维灵活性。在初中数学的学习之中，要熟练地运用化归思想解答问题，就需要学生具备灵活的数学思维，认真观察，结合发展规律，运用数学思维看待变化的事物，提出解决实际问题的方法和设想[2]。在学习新的知识的时候，能够迅速地和原有的知识建立联系，将新的知识纳入到知识体系。在进行问题解决的时候，能够有针对性的找到解题的方法，不断地进行策略调整。灵活思维的培养需要从学生日常观察和联想开始做起，因此教师在教学中要鼓励学生积极思考，认真观察。数学题目之中，往往包含了很多条件，教师要引导学生进行认真地观察，通过思考找到问题的本质，从而清晰解题的思路，解决问题。此外还要注意对学生联想能力的培养，能够根据一个知识点联想到相关的其他知识点，将数学的学习由简化繁再由繁化简。教师要帮助学生建立知识体系，引导学生认真观察积极思考，多角度地思考问题，解决问这样不仅能够促进学生思维灵活性的提升，也有助于学生知识的吸收和运用。

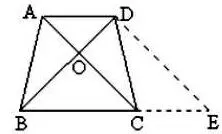
图1

例如，如图1所示，AD//BC,AB=CD,对角线AC、BD相较于O,AC⊥BD,AD=4,BC=6,求AC的长。解：过D点作线DE使DE//AC,并交BC的延长线于E点，且AD=CE,已知AC=DE,所以BE=BC+CE=10.AC⊥BD，DE//AC，AD//CE，所以ACDE是平行四边形，BD⊥DE,∵AB=CD,∴BD=AC,BD=DE根据直角三角形的性质从而得出AC的长度。再如，在学习相似三角形的有关知识的时候，可以通过三条边之间的关系来得出相似三角形的结论。“如果两个三角形为相似三角形”那么对应的两条边成比例且夹角相等，还可以通过三角形内角的度数来进行判定，如果两个三角形对应的角相等，那么这两个三角形就是相似三角形。在进行这些问题的解答的时候，学生只有认真地进行观察和联想才能够多角度的寻找解决问题的方法。

2.3 运用化归思想化数为形。初中数学中很多知识都是相通的，在一定的条件下可以互相转化。在代数的学习中遇到难点时，教师可以引导学生将代数问题进行转化，变成简单的几何问题或者学生熟悉的问题进行解答。例如，已知三角形ABC的三条边分别为m2-n2、m2+n2、2mn，求三角形的面积。这个问题就是利用三个边来求三角形的面积，如果运用代数的方式求解相对比较繁琐，如果能够用几何的方式更加方便容易。因为(m2+n2)2-(m2-n2)2=(2mn)2，三角形的三条边满足勾股定理的逆定理，所以这个三角形是直角三角形，所以三角形的面积1/2(m2-n2)2mn=mn(m2-n2)。这样求解相对就比较简单了，降低解题的难度。

在初中数学的学习中，教师在教学中要认识到化归思想的重要性，不仅要讲解教材的理论知识，同时还要培养学生多角度思考问题的能力，帮助学生建立数学思维，运用化归思想建立知识的联系，从而使学生对数学知识有更加深入的认识，提升学生的学习效率，提高学生的数学水平。