基于Z变换的C-R逆算子分析及其应用研究

金幼贤 周建斌,3 马英杰 岳爱忠 洪 旭 刘 易 王 敏

1（成都理工大学 核技术与自动化工程学院 成都 610059）

2（中石油测井公司 西安 710032）

3（四川新先达测控技术有限公司 成都 610052）

在核辐射测量过程中，原始脉冲信号经过电路系统后，得到的是经电路系统处理与变换的信号。比如，阶跃信号经过C-R（电容-电阻）微分电路系统得到负指数信号；经探测器输出的负指数信号经过C-R微分电路系统得到带下冲拖尾的指数信号；比较宽的脉冲信号经过极零相消电路（Pole-zero Cancellation，PZC）系统后得到比较窄的脉冲信号；探测器负指数信号经过S-K成形系统得到类高斯形态的信号等。为避免经电路系统变换后信号失真或畸变，进行高计数率、高精度、高分辨的能谱测量，原始核脉冲信号的获取十分重要，但实际电路系统中不存在逆系统，即信号只能通过电路处理系统正向传输，而无法通过模拟电路系统处理逆向恢复。

目前核辐射信号数字处理的数字处理研究方法主要可以分类为卷积变换、拉普拉斯变换、Z变换以及傅里叶变换等方法。而采用拉普拉斯变换求解的核电子学电路输出的结果是理论上的结果，辐射探测过程中的核信号含有噪声、堆积等诸多成分，所以该解析解难以被应用于实际辐射探测。在早期的研究工作中，Jordanov等［1-4］基于Z变换研究了高分辨率能谱下的实时数字递推算法，包括对称梯形成型、三角成型、对称尖顶成型等多种算法，并将其部署到实际数字成型器中，对其性能进行了细致的研究；成都理工大学的喻杰等［5-6］利用拉普拉斯方法，得到了C-R、R-C以及极零相消电路和低通S-K滤波成形电路的输出信号，并通过MATLAB模拟了负指数输入信号时的不同输出信号；周建斌等［7-8］对核电子学中常见的电路进行了推导，分别给出了递推算法，并结合基于拉普拉斯变换推导出来的结果运用VBA（Visual Basic for Applications）工具进行了算法对比；Nakhostin等［9］基于Z变换推导了CR-RCn多级串联滤波器的递推算法；Hong等［10］基于Z变换推导了双指数冲激响应，对辐射测量中的计数率进行了校正，并取得了不错的效果；Zhang等［11］对一般意义上的S-K（Sallen-Key）滤波器电路参数与最终的成型结果的关系进行了研究，并得到了最接近高斯成型的参数的选取方式，他们还给出了4种数字化的反向放大成型滤波电路，包括反向放大电路、改进的反向放大电路、多种反馈的反向放大电路和三阶多重反馈放大电路，并对这些数字电路的幅频特性进行了细致的研究，结果表明：多重反馈反向放大电路兼具较优的幅度提取和噪声抑制特性［12］。这几种变换方法的应用多种多样，其中Z变换的效果最好，且应用最广泛。在核电子学测量中，一般将辐射探测器与前置放大器结合在一起做成探头，而后经过调理电路，信号被数字化以后在数字电路将被进一步处理［13］，这种架构意味着数字信号处理部分的算法将对最终的幅度和计数率的测量的准确度起到重要的作用，故对数字处理部分的算法研究意义重大。

本文在前期核信号数值分析基础上，基于Z变换，以阶跃信号和负指数脉冲信号为例，构建了逆系统分析方法，针对C-R电路系统得到了C-R逆算子，并对基线漂移问题进行了分析研究，这两部分算法可以根据不同的探测器输出的信号的特点进行参数调整，部署在后级的数字信号处理（Digital Signal Processing，DSP）中。

1 基于Z变换的C-R系统数值分析

辐射探测器的输出信号一般可以分为两类：即对于开关复位型探测器（如硅漂移探测器(Silicon Drift Detector，SDD)）与fast SDD探测器，其输出信号为阶跃信号，对于常规的探测器如NaI探测器，其输出信号为负指数信号。

C-R微分电路（图1）是一种高通滤波电路，是核电子学中一种常用的简单成形电路，主要用于信号的交流耦合，或者信号的解调等，其中的R、C器件的参数值一般依据后级电路的分析需要来确定。

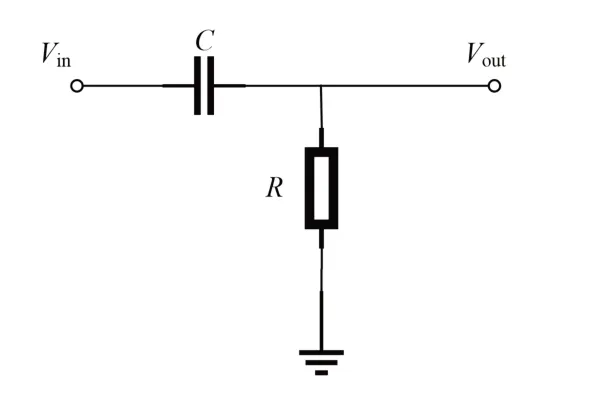
图1 基本的C-R微分成形原理图Fig.1 Schematic diagram of C-R differential circuit

图1中Vin为输入信号，Vout为输出信号。基于此，本节旨在以阶跃信号与负指数信号为研究对象，对这些信号相应的变换进行分析。

当输入信号为阶跃信号时，不妨设其幅度为A，则输入信号的Z变换结果如式（1）所示；不妨设该电路的时间常数为τ1=RC（其中R与C分别是图1电路中电阻阻值和电容容值），其相应的输出信号为负指数信号，其数学表达见式（2），a1=exp（-ΔT/τ1），ΔT是采样时间，则输出信号的Z变换结果如式（3）所示。

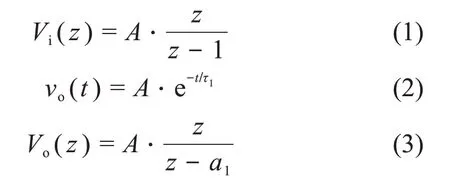
由Vi（z）和Vo（z），可得C-R电路系统在Z域的传递函数：

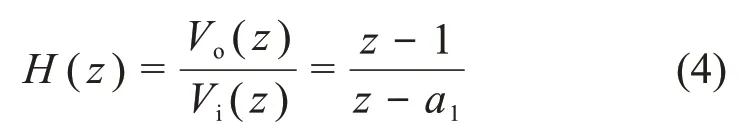
由传递函数可得输出信号的Z域函数为传递函数与输入信号的Z域函数的乘积：

式（5）两边同乘以（z-a1），并展开整理，得：

把式（6）进行逆Z变换，即可得到离散数值递推解：

由于a1中的ΔT/τ1是一个比较小的值，所以可以泰勒展开进行近似，同时，取k=ΔT/τ1，即可得到该项近似解为：

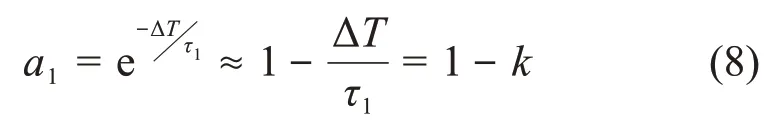
将式（8）代入式（7），可得该系统对阶跃输入信号的离散数值递推公式：

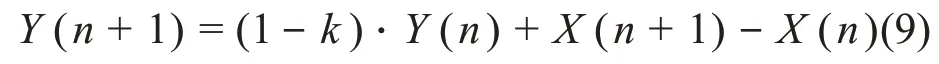
而对C-R系统进行分析，其数值解如式（10）所示。

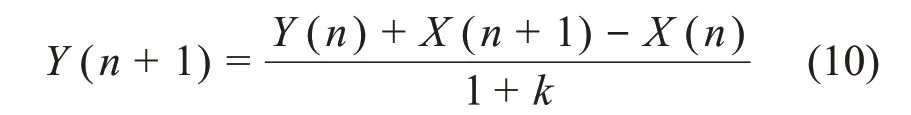
若输入信号为负指数核脉冲信号如式（11）所示，其相应的时间常数为τ，设a=exp（-ΔT/τ），则输入信号的Z变换结果如式（12）所示。

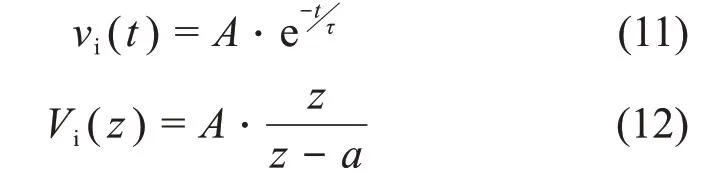
对C-R电路，结合拉普拉斯变换，可得到单指数信号经C-R电路后的输出信号时域函数解如式（13）所示，输出信号的Z变换结果见式（14）。

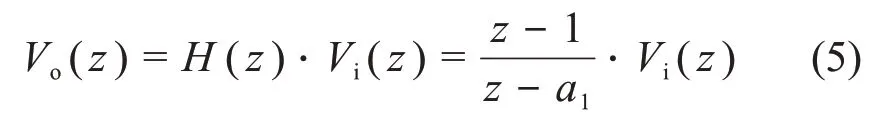
由Vi（z）和Vo（z），可得C-R电路系统在Z域的传递函数：

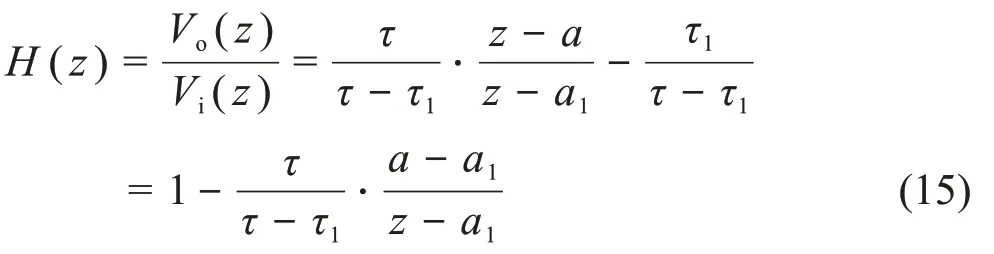
则Z域的输出信号，等于传递函数与Z域输入信号的乘积，代入得式（16）。

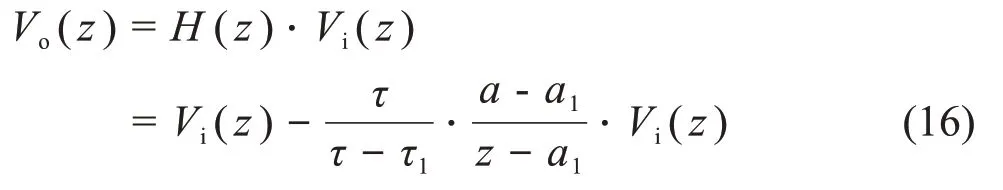
式（16）两边同乘以（z-a1），并展开整理，得式（17）：

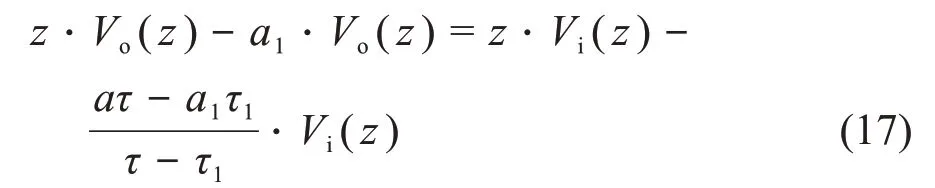
把式（16）进行逆Z变换，即可得到离散数值递推解：

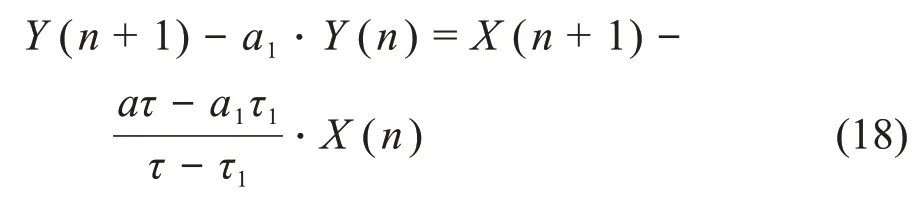
由于ΔT/τ是一个比较小的值，所以可以泰勒展开近似到一次项，得该项近似解为：

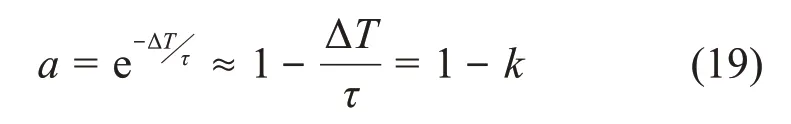
同理，将式（8）和式（19）代入式（18），可得式（9），即无论输入信号为阶跃信号、或单指数信号，C-R电路的离散数值递推公式相同，由此可见，递推公式（10）可作为C-R电路的数值递推计算公式。

C-R微分成形电路可用于有载波信号时的核探测器信号的提取，因此我们用式（10）模拟了连续阶跃信号基本的C-R微分效果，如图2（a）所示。阶跃信号的幅度分别设置为1 000、1 500、2 000、3 000和4 000，参数k=0.025（即ΔT=50 ns，C取值1 nF，R取值2 kΩ，RC=2 000 ns=2μs）。结合Z变换结果式（7）、对Z变换进行泰勒简化后的结果式（9）和C-R电路的数值解式（10）对阶跃的输入信号进行递推计算，得到相应的输出信号，结合输出信号的结果曲线图，这三种算法的结果基本保持一致。

同样，当输入信号为负指数信号（νi（t）=1 000e-1/τ，τ=5μs），基本可以模拟气体探测器或者半导体探测器的输出信号。输出信号1为k=0.025时的模拟情况（ΔT=50 ns，C取值1 nF，R取值2 kΩ，RC=2 000 ns=2μs）。输出信号2为k=0.002时的模拟情况（ΔT=50 ns时，C取值1 nF，R取值25 kΩ，RC=25 000 ns=25μs）。模拟结果如图2（b），结合输出信号的结果曲线图，这三种算法的结果基本保持一致。

图2 连续带噪声阶跃信号经C-R系统的数值模拟(a)和带噪声负指数信号经C-R系统的数值模拟(b)（Num_so代指数值解的曲线，Z_so指代Z变换解的曲线，Tal_so则指代经过泰勒展开以后的解的曲线）Fig.2 Simulation for continuous step-signal with C-R system(noise added)(a),minus-exponential signal with C-R system(noise added)(b)(where Num_so denotes numerical solution,Z_so denotes Z transform solution and Tal_so denotes Z transform simplified with Taylor expansion)

2 C-R逆算子的构建

将数值递推公式（9）逆推，则可以反解得到X［n］的递推公式：

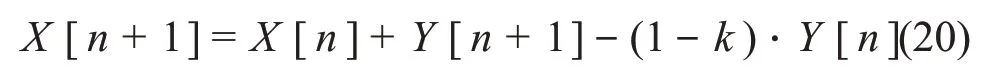
我们将式（20）定义为C-R逆算子的数字递推解。Y［n］为经C-R微分电路后的数字化输出信号，X［n］为未经C-R微分电路的数字化输入信号，Y［n］与Y［n-1］之间的时间为数字化采样时间ΔT。

为适于FPGA的运算，设M=1/k，将式（20）两边同时乘上M，得到式（21），设f［n+1］=M·X［n+1］，即Y［n］是X［n］的M倍，可得到式（22）。假设式（20）或式（22）中的Y［n］表示的是经C-R电路系统输出的信号经数字化采样得到的输出信号数字化序列，则X［n］表示经过逆运算得到的C-R电路的实际输入脉冲信号的数字化序列。

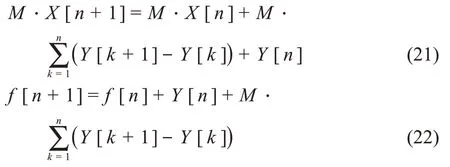
把式（22）再如式（23）进行数值积分变换，设f［1］=0，Y［0］=0，则式（23）可以变成式（24）。

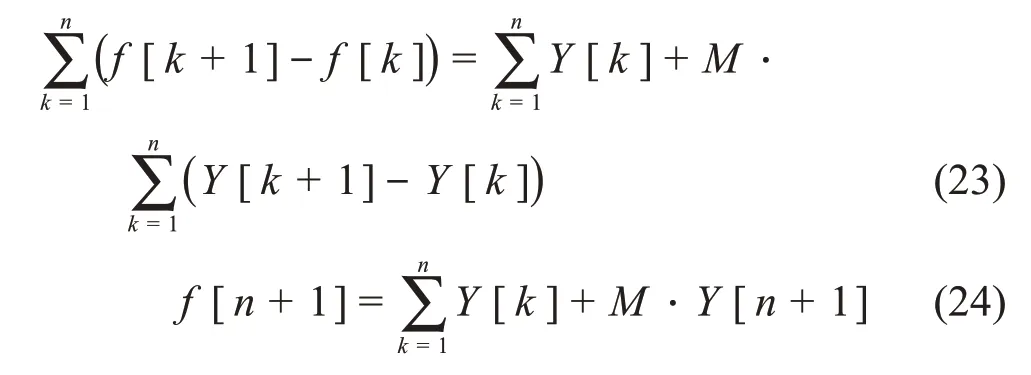
把累计求和项加个Y［n］，整理式（24），得式（25），即式（25）为C-R逆算子的数字解，由此，设计FPGA数字系统的实现框图如图3所示。

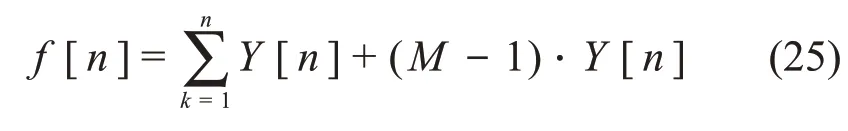
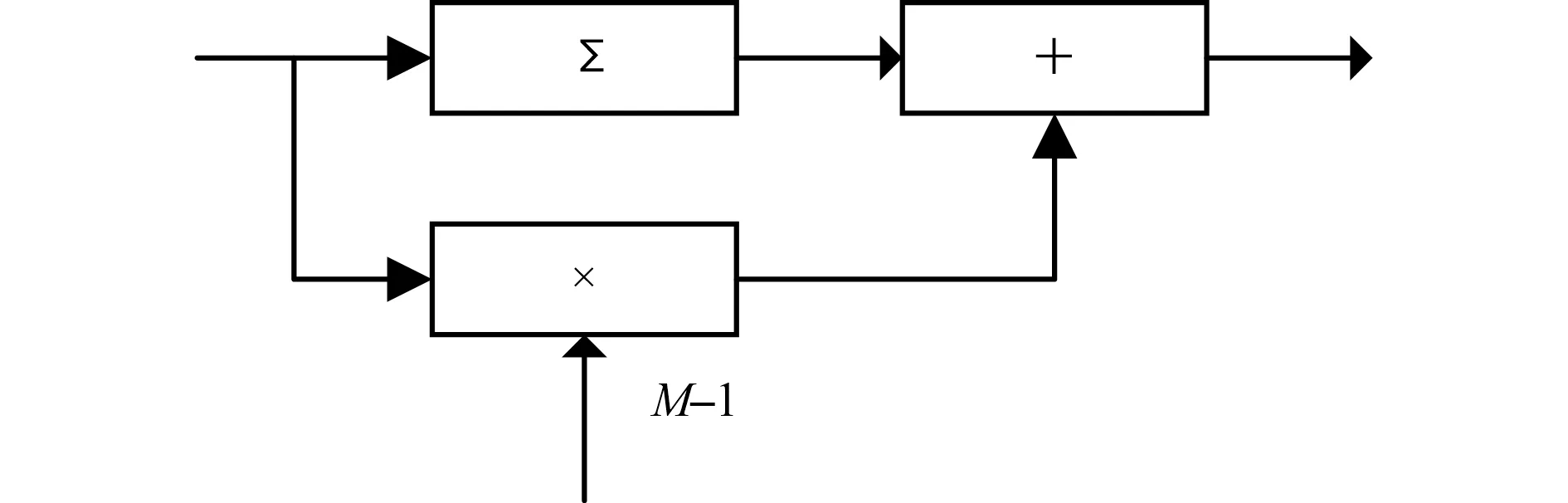
图3 C-R逆算子的FPGA数字化实现框图Fig.3 Block diagram of implementation of inverse C-R transform in FPGA

3 C-R逆算子的初步应用研究

我们利用前文得到的C-R逆算子，对单指数核脉冲信号通过C-R系统后产生的反冲拖尾现象进行应用研究。如图4所示，单指数核脉冲信号经过一个C-R微分电路，产生一个窄的带反冲的信号，这个反冲在高计数率情况下会影响信号基线，造成谱漂移，若能消除反冲即可解决这个问题。考虑时间常数为τ的单指数核脉冲输入信号（则可以定义其数学表达式为νi（t）=Ae-t/τ），C-R微分电路的时间常数为τ1，则输出的脉冲信号为式（26）。反之，若原始输入的单指数核脉冲信号的时间常数为τ1（亦即表达式为vi(t)=A·e-t/τ1，C-R微分电路的时间常数为τ，则输出的脉冲信号仍如式（26）。由此可见，微分顺序不影响最终结果。

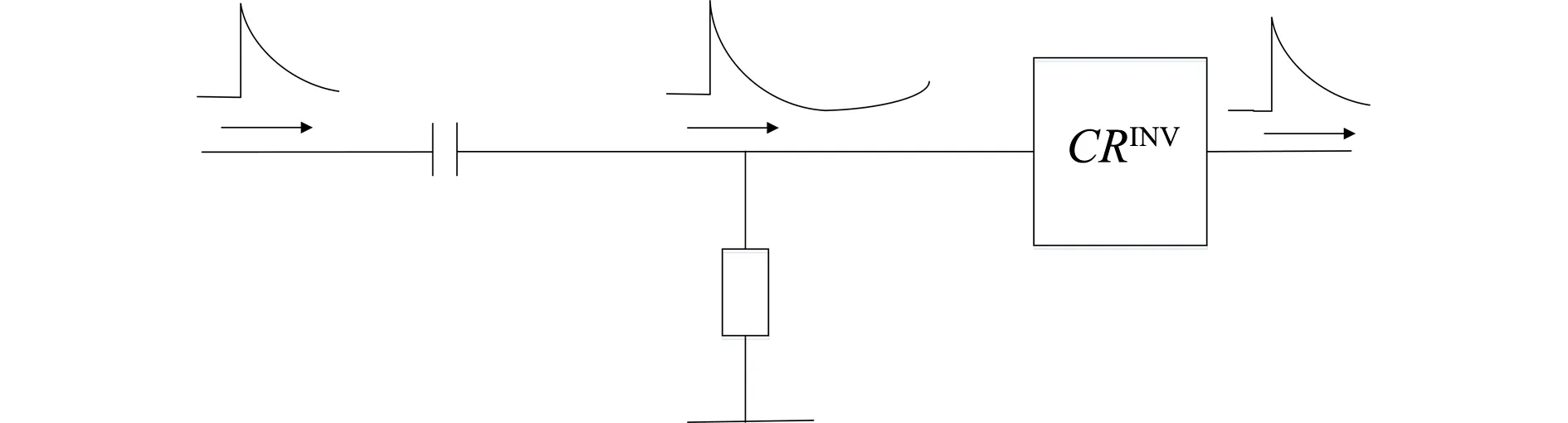
图4 C-R逆算子运算形式及效果Fig.4 Effect of inverse C-R transform

下面将针对C-R逆算子得到的带反冲拖尾信号的反冲拖尾消除，生成新的无反冲窄单指数核脉冲信号进行讨论。首先，如果将经C-R微分电路的带反冲拖尾的信号，做C-R逆算子运算，若选取逆运算系统的参数与C-R系统的时间常数相同，显然经过逆运算生成的信号的时间常数与原始信号的时间常数相同，为原始的单指数核脉冲信号；而若选取C-R逆算子的参数与初始信号的时间常数相同，那么经过逆运算所生成的信号的时间参数与C-R系统的时间常数将相等。结果表明：如果将C-R系统的时间常数选取的较之于原始信号的时间常数小，则可以在调试C-R逆算子时，获得一个具有较小时间常数，即宽度变窄的无反冲拖尾的信号，下面将就这一点进行仿真验证。

如图5所示，产生一个添加了噪声的输入负指数信号（Input minus-exponential signal），然后通过C-R系统，输出带有下冲的负指数信号（Output undershoot exponential signal），而后让该带有下冲的输出信号通过同等参数的C-R逆系统，得到逆变换的输出指数信号（Inverse exponential signal）。具体参数设置包括带噪声的单指数核脉冲信号（图5中黑色线条所示，时间常数为2μs，正态分布噪声幅度设置为20），通过C-R微分电路（时间常数为625 ns），得到带反冲拖尾的输出信号（图5中红色线条所示），将此信号做C-R逆算子运算，时间常数取为单指数核脉冲信号的时间常数，即2μs，得到了窄的无反冲的单指数核脉冲信号（模拟效果如图5中蓝色线条所示）。这里的变换说明，使用C-R逆系统对下冲负指数信号进行处理的时候，若使参数与原始输入的核信号时间常数相匹配，可以有效消除信号的下冲与拖尾，在C-R成型系统的时间常数较核信号时间常数相等的前提下，可以得到变窄的负指数核脉冲信号。

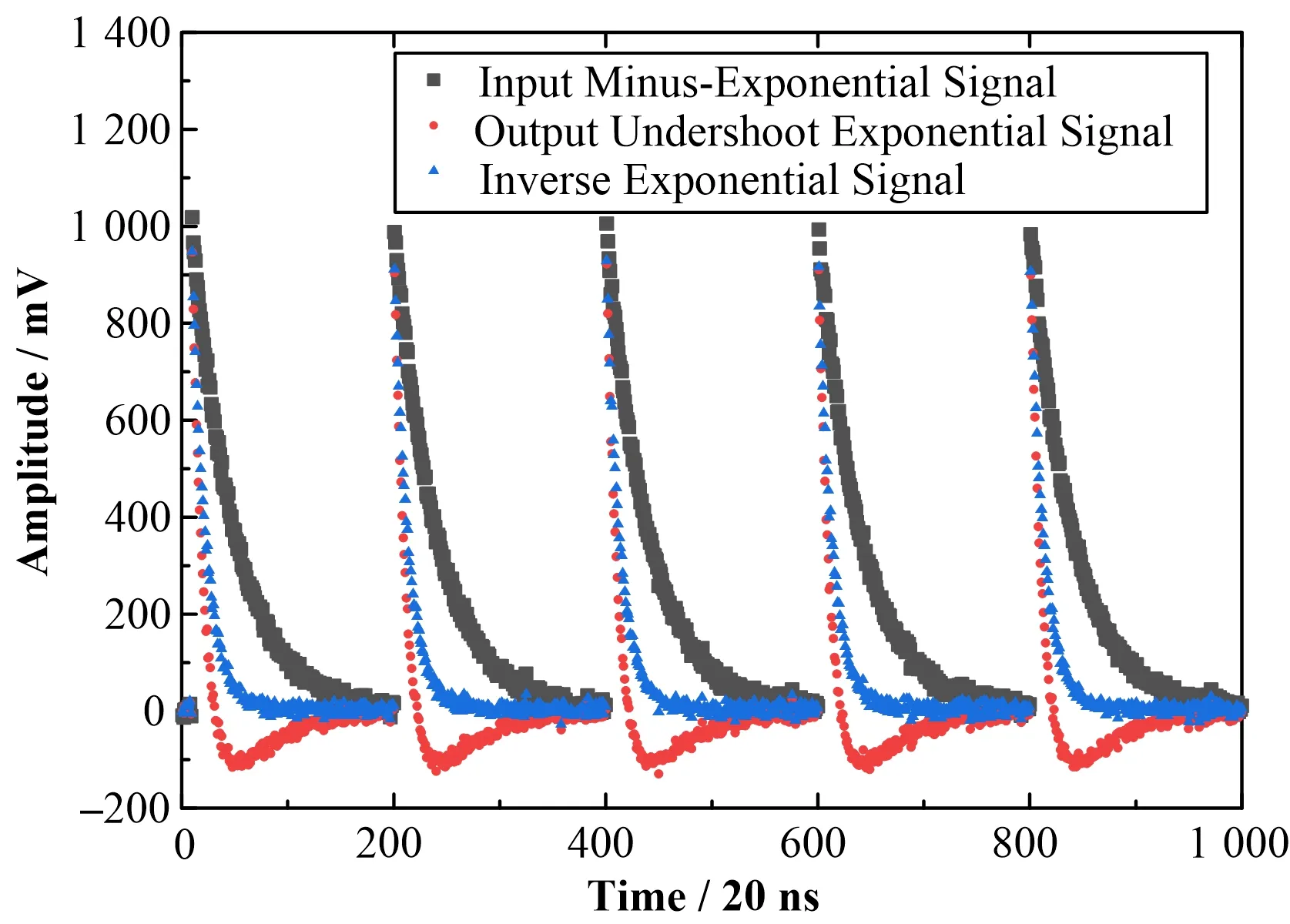
图5 C-R逆算子运算模拟（无漂移，基线=0）Fig.5 Simulation for inverse C-R transform(without baseline drift)

4 基线漂移问题的分析

实际测量时核脉冲信号通过C-R电路系统后，还会经过后级的信号处理才会进入ADC采样，所以会存在一个基线不在零点的问题，这里对基线不在零点经过C-R逆算子后会产生的效果进行了模拟。

图6模拟了基线为小于零（仿真模拟参数选取为-10）的情况。带噪声输入负指数信号经过C-R电路系统输出为基线稳定在-10的一个下冲长拖尾的负指数信号，而后经过C-R逆系统变换以后，得到了一个消除了反冲，但出现负向漂移的输出信号。

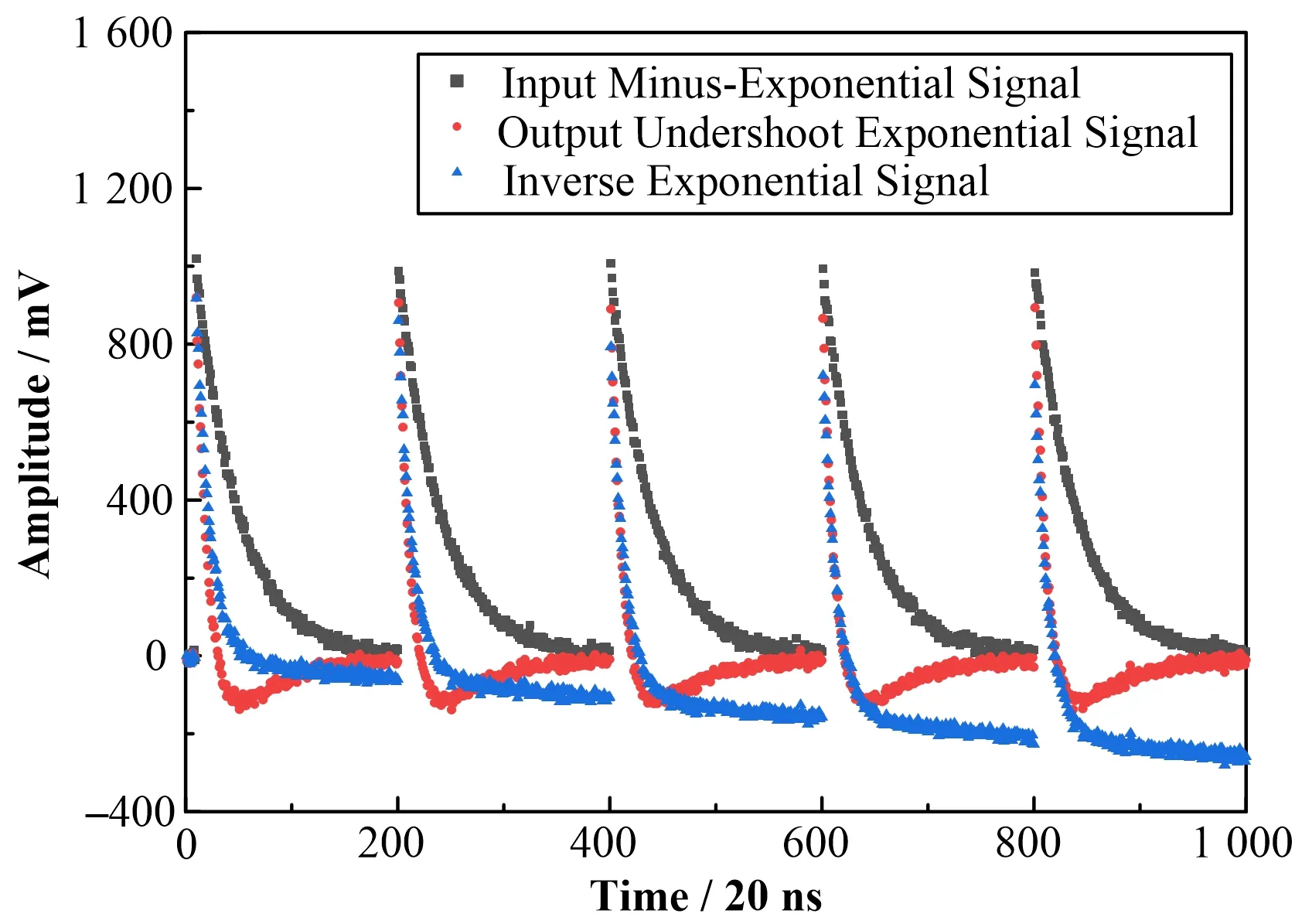
图6 C-R逆算子运算模拟（负向漂移，基线=-10）Fig.6 Simulation for inverse C-R transform(with baseline drift of-10)

图7模拟了基线为大于零（仿真模拟参数选取为+10）的情况。带噪声输入负指数信号经过C-R电路系统输出为基线稳定在+10的一个下冲长拖尾的负指数信号，而后经过C-R逆系统变换以后，得到了一个消除了反冲，但出现正向漂移的输出信号。

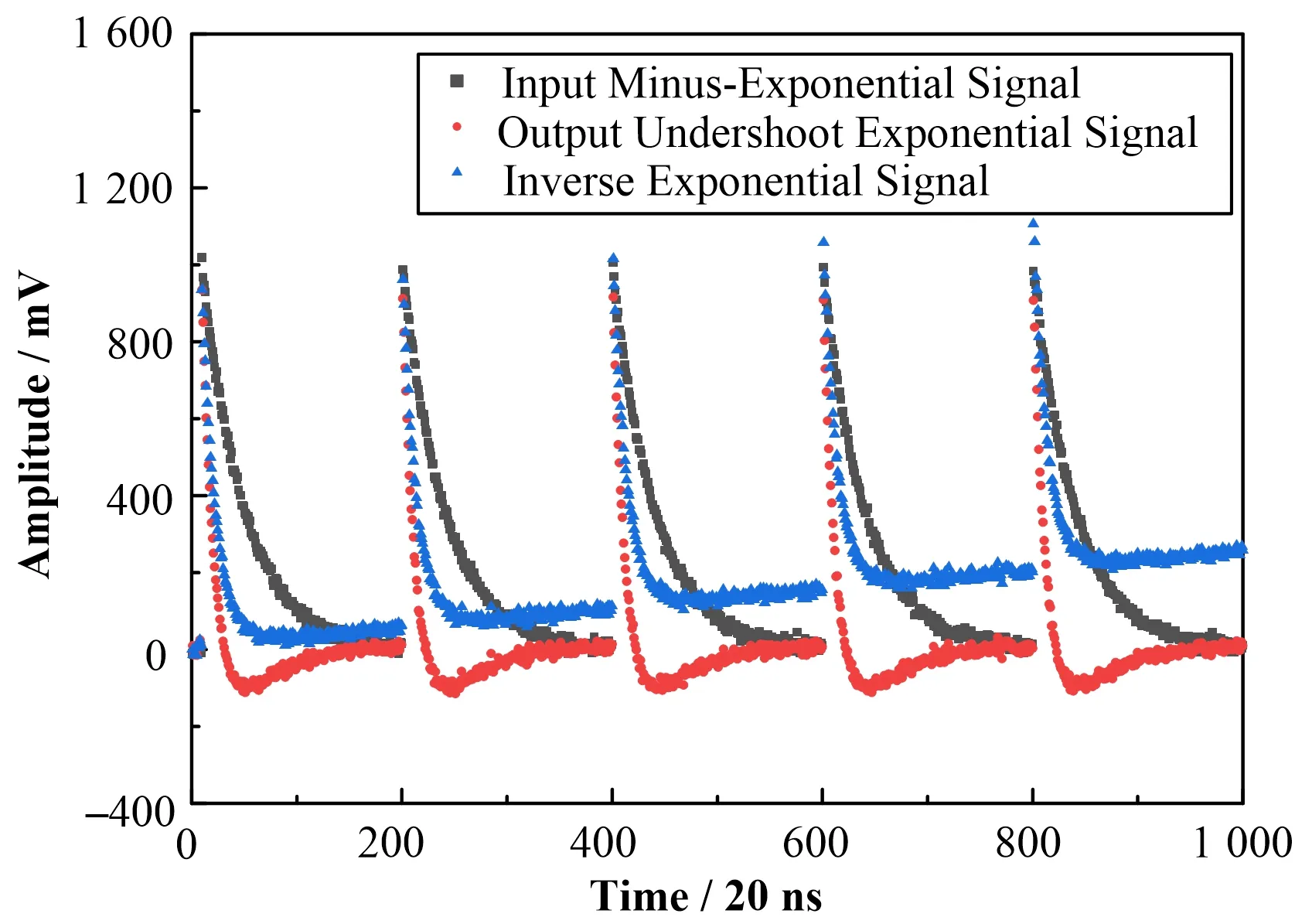
图7 C-R逆算子运算模拟（正向漂移，基线=+10）Fig.7 Simulation for inverse C-R transform(with positive baseline drift of+10)

在式（25）的C-R逆系统表达式中，包含一个累加项，对于一个基线为零的单个单指数信号，经过C-R电路后，信号有反冲拖尾，但其整个信号的积分为零，即正信号部分的积分与负信号部分的积分相等，则累加项的累加结果会为零，不会出现系统性的漂移；如果正信号部分的积分大于负信号部分的积分，则累加项在累加后会一直大于零，出现数字基线正漂移；如果正信号部分的积分小于负信号部分的积分，则累加项在累加后会一直小于零，使得出现数字基线负漂移现象。出现这种情况的原因实际上是出现了C-R逆算子的多解性问题，或者是C-R正系统的多种信号同样结果的问题，把漂移后的信号经过C-R正系统后又都能恢复到同样的原始信号，说明三个解都是对的，只是C-R逆算子对直流成分产生了作用，而实际的C-R系统对直流成分是不起作用，这就是数值信号处理中基线漂移的产生原因。

因此，要解决这种数字基线漂移问题，在ADC转换精度足够的前提下，在C-R逆算子的累加项改进其表达式如式（27），也就是累加项计算时扣除数字基线值。或者在数字采样时，增加有效脉冲判别，来脉冲时累加器才开始工作，脉冲过后累加器自动清零，没脉冲时系统输出数字基线。

式中：Dbase为测量系统的实时测量基线值，该参数在实际系统测量时可以估计出来。

图8模拟了改进累加项的C-R逆算子算法，在基线为+200时的C-R逆算子无漂移恢复仿真实验。输入信号为带噪声的基线为+200的负指数信号，经过C-R电路系统的输出为带反冲长拖尾的输出信号，而后经过改进的C-R逆算子运算后，消除了逆系统运算中存在的基线漂移，实际测量时可能会存在基线测量不稳定情况或者电子学噪声的影响，可能还会存在小的漂移。

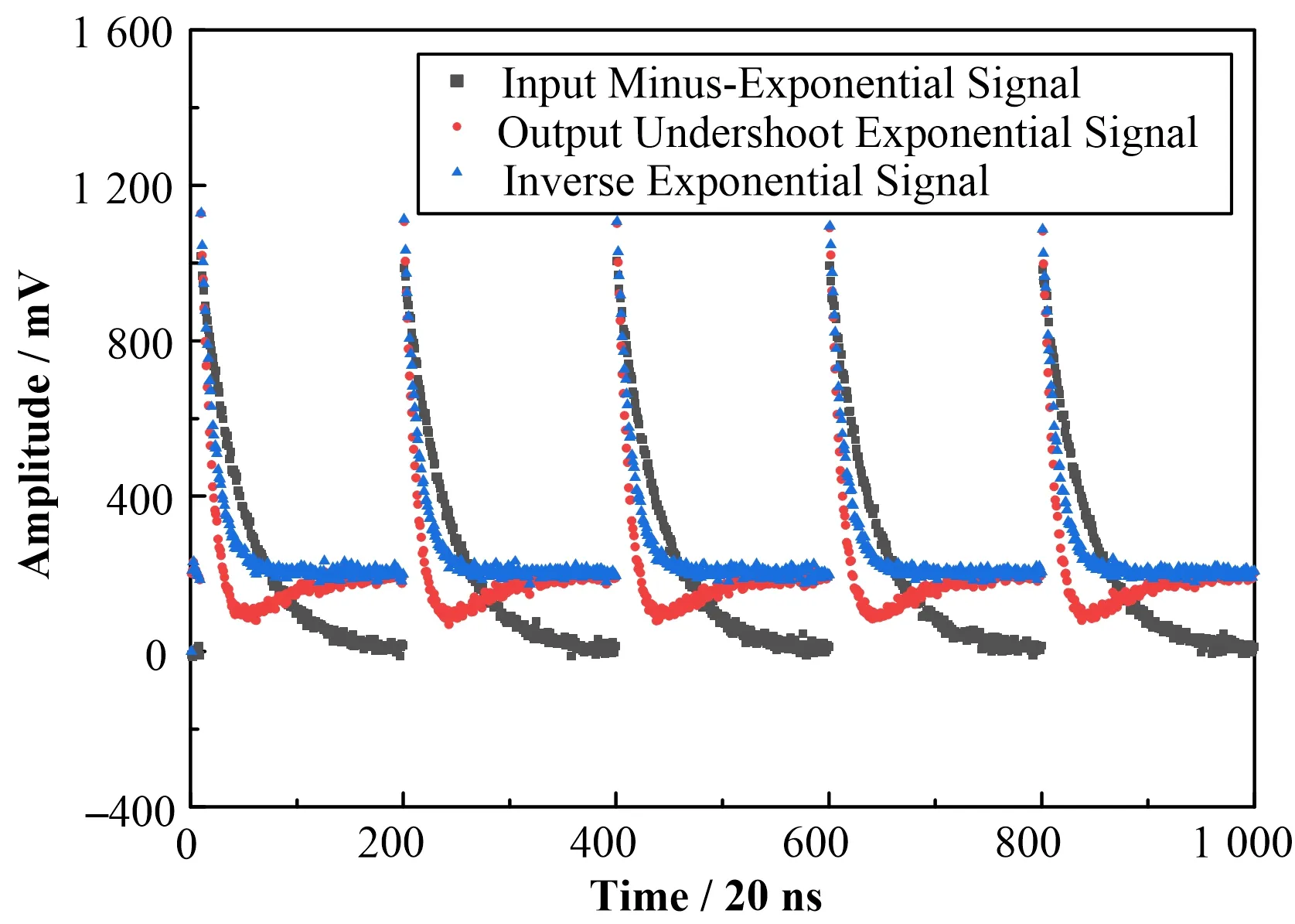
图8 C-R逆算子运算模拟（无漂移恢复，基线=+200）Fig.8 Simulation for inverse C-R transform(recovery of drift with positive baseline drift of+200)

除此之外，不同的探测器针对不同的辐射源其输出的信号的特点不同，可以是阶跃信号，也可以是指数信号，而且，信号的幅度与宽度影响因素比较多，经过前置放大器的调节，以及调理电路的匹配，在DSP中可以对本文中提出的C-R逆算法与抑制基线漂移的算法的参数进行调整，以实现对不同探测器输出信号的处理。

5 结语

本文通过对C-R电路系统进行Z变换数值分析，得到了C-R电路系统的数值递推解，再逆向分析从数学上得到逆C-R系统的数值解，并且构建了CR逆系统算子。基于得到的C-R逆算子，对负指数核脉冲信号通过C-R系统后产生的反冲拖尾信号进行了初步应用研究，研究表明：1）当C-R逆系统参数与原始核信号的时间常数相同时，即可得到消除反冲的窄脉冲信号，输出的信号的时间常数与C-R系统的参数一致，在C-R成型系统的时间常数比原始核信号的时间常数小时，基于级联C-R系统的无序性，不仅可以实现数字极零相消，还可以获得变窄的核脉冲信号；2）分析了C-R逆算子数字基线漂移的原因，提出了新的数字基线恢复方法，得到了C-R逆算子的改进算法，并模拟实验验证了该方法可行。