具有无症状的疟疾传播模型的最优控制和敏感性分析
2021-07-17王义琳郑庭庭聂麟飞
王义琳,郑庭庭,聂麟飞
(新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)
疟疾是一种通过携带疟原虫的蚊虫叮咬进而感染所引起的媒介传染病.临床医学研究表明,疟疾感染者一般会在被携带疟原虫的蚊虫叮咬7 d或之后才出现症状,最初表现的症状可能很轻而难以被发现.此外,由于个体之间的差异,许多疟原虫携带者因症状轻微而被忽视,故在疟疾的传播过程中无症状感染者是普遍存在的[1].然而,在现有的研究工作中,往往只考虑了受感染个体的影响,而忽略了无症状个体在疾病传播中的重要作用.[2]为此,一些国内外学者建立了具有无症状感染的传染病数学模型去讨论无症状感染在传染病传播和控制中的影响[3-4],研究表明,人群中无症状感染者的比例和无症状感染者的病程周期是影响疾病患病率的最重要参数.
1 模型的建立
用Sh(t),Sv(t),Ia(t),Is(t),Iv(t)和Rh(t)分别表示t时刻的易感者、易感蚊子、无症状感染者、有症状感染者、感染蚊子和恢复者的数量或密度.则人类和蚊子总数为Nh(t)=Sh(t)+Ia(t)+Is(t)+Rh(t)和Nv(t)=Sv(t)+Iv(t).考虑无症状感染者和种群总数对疾病传播的抑制作用,用饱和发生率模拟疟原虫在人和蚊子间的传播.基于疟原虫在蚊虫和人体内的传播规律,提出具有无症状感染的疟疾传播模型:
(1)
其中:1/μh,1/μv分别表示人类与蚊子的平均寿命,取值分别为70 a[5]与14 d[6];βvh,βhv,γa与γs分别表示染病蚊子对易感人群的感染率、染病人类对易感蚊子的感染率、无症状个体的恢复率与有症状个体的恢复率,取值范围详见文献[7-8];参数Λh,Λv,αi,c,p与θ分别代表人类种群的补充率、蚊子种群的补充率、饱和系数、蚊子的有效控制系数、无症状感染者向易感蚊子传播疾病的可能性和个体在感染后成为无症状病例的可能性,αi,c,p与θ的取值均在(0,1)之间.
2 平衡点的动态分析
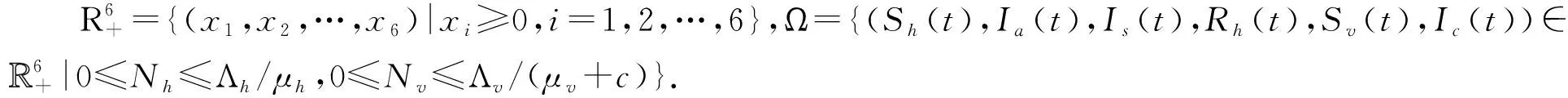
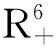
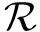
通过计算下一代矩阵FV-1的主特征值或谱半径,得到如下基本再生数:
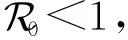
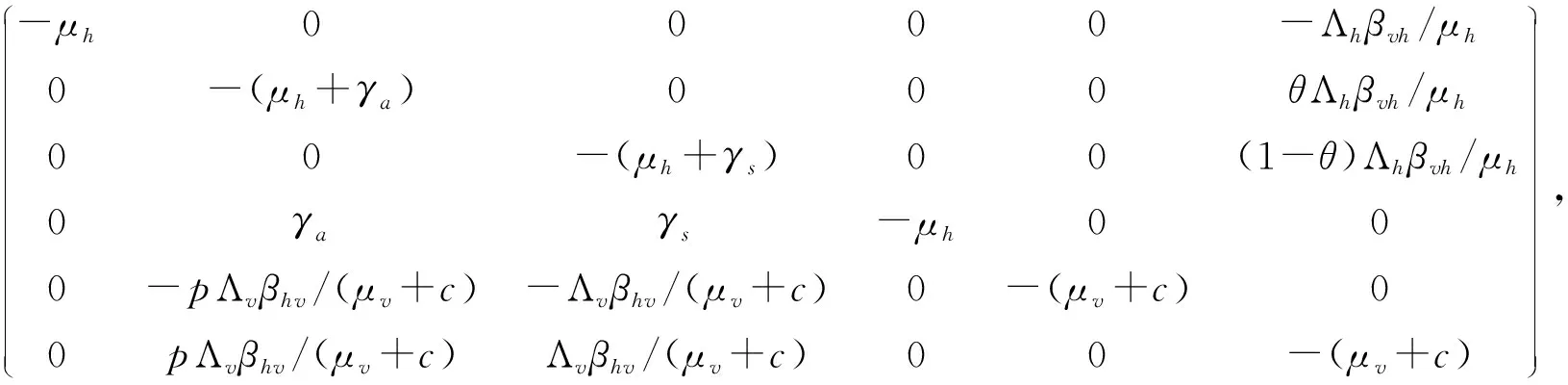
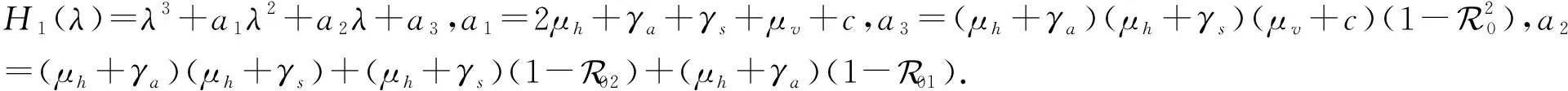

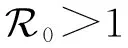
通过适当选取Lyapunov函数,类似定理2的证明,可得下面结论:

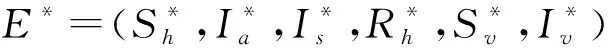
显然有
(2)
(3)
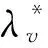
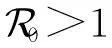


证明由模型(1)的第1和第5个方程可知
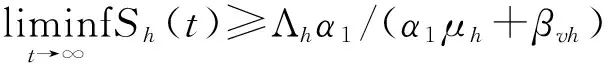
下证M∂={(Sh,0,0,Rh,Sv,0)|Sh>0,Rh≥0,Sv>0}.事实上,若(Sh(0),…,Iv(0))∈M∂,则有Ia(t)≡Is(t)≡Iv(t)≡0.否则,若存在一个t0≥0使得Ia(t0)>0,或Is(t0)>0,或Iv(t0)>0成立,则有(Sh(t),…,Iv(t))∈X0.这与(Sh(0),…,Iv(0))∈M∂矛盾.
记w(Sh(0),Ia(0),Is(0),Rh(0),Sv(0),Iv(0))为从(Sh(0),Ia(0),Is(0),Rh(0),Sv(0),Iv(0))∈X出发的解的w极限集.令Ω′=∪{w(Sh(0),Ia(0),Is(0),Rh(0),Sv(0),Iv(0))|(Sh(0),Ia(0),Is(0),Rh(0),Sv(0),Iv(0))∈M∂},则在M∂上有Ia(t)=0,Is(t)=0和Iv(t)=0.从而在M∂上模型(1)退化为
(4)
显然,模型(4)存在唯一的平衡点E01=(Λh/μh,0,Λv/(μv+c))且是全局渐近稳定的.因此,E0是模型(1)在M∂上的唯一平衡点且全局渐近稳定的.因此Ω′={E0},且E0为Ω′的一个孤立的非循环的覆盖.
最后,证明
(5)
其中(Sh(t),Ia(t),Is(t),Rh(t),Sv(t),Iv(t))是模型(1)满足初值(Sh(0),Ia(0),Is(0),Rh(0),Sv(0),Iv(0))∈X0的解.由文献[10]可知,若Ws(E0)∩X0=∅成立,Ws(E0)为E0的稳定流形,则(5)式成立.假设Ws(E0)∩X0=∅不成立,则存在一个(Sh(0),Ia(0),Rh(0),Sv(0),Iv(0))∈X0使得从该初值出发的解(Sh(t),Ia(t),Is(t),Rh(t),Sv(t),Iv(t))∈X0,当t→∞,有
Sh(t)∈Λh/μh,Ia(t)→0,Is(t)→0,Rh(t)→0,Sv(t)→Λv/(μv+c),Iv(t)→0.
(6)
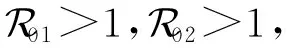
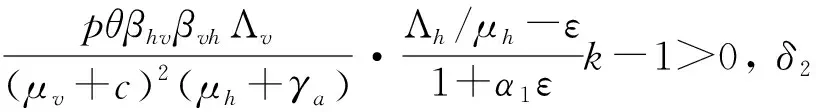
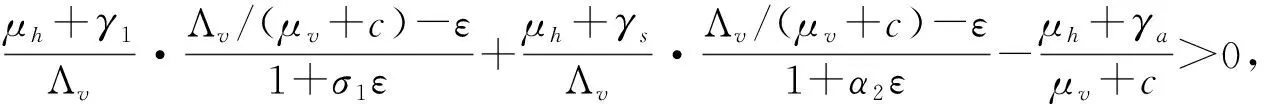
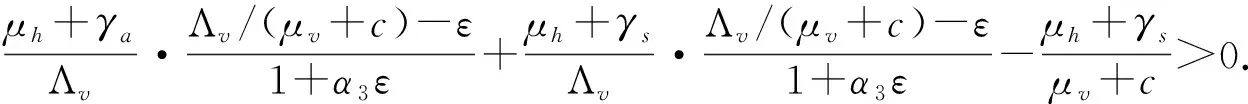
进一步,由(6)式可知,对上述的ε,存在一个T>0使得
(7)
令W(t)=Ia(t)+Is(t)+ρ1Iv(t)+ρ2Iv(t),ρ1和ρ2是待定正常数,则W(t)沿模型(1)的全导数为
选取ρ1=(μv+c)(μh+γa)/(pβhvΛv),ρ2=(μv+c)(μh+γs)/(βhvΛv),代入上式并结合(7)式可得
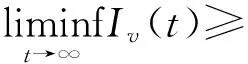
3 敏感性分析
敏感性分析可以用来描述模型参数关于基本再生数的敏感度.当基本再生数是参数的可微函数时,可以用偏导数交替法定义敏感性指数.
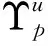

表和关于模型(1)中参数的敏感性指数
4 最优控制
由于疟疾没有疫苗,仅能依赖于药物的治疗,因而媒介控制就显得尤为重要.为此,提出了一个最优控制问题,目的在于找到一种可行的解决方案使得无症状个体的数量,有症状个体的数量和蚊子的总数量与控制成本之间最小化,从而控制疾病的传播.假设u(t)和c(t)分别代表个体自我保护意识和媒介防控的控制变量,则该控制问题可以表示为
(8)
根据上述模型,给出目标函数最小化的最优控制问题如下:
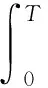
(9)
这里:A1,A2和A3分别表示无症状个体、有症状个体和蚊子总数的权重常数;B1和B2分别表示易感个体和蚊子控制因子的权重常数.控制集的可行域为U={(u(t),c(t))|0≤u(t),c(t)≤1},u(t)和c(t)在[0,T]上是勒贝格可积的且模型(8)是线性有界系统,从而满足最优控制存在的条件.
定理6 存在(u*(t),c*(t))∈U,使得在控制模型(8)的约束下给出的目的函数(9)达到最小,即
J(u*(t),c*(t))=min{J(u(t),c(t))|(u(t),c(t))∈U}.
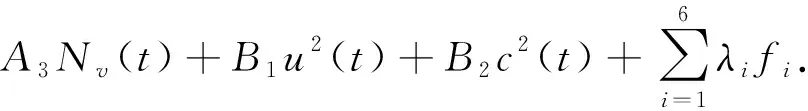
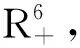
横截条件为λi(T)=0,i=1,…,6.此外,最优控制J(u*(t),c*(t))满足
5 数值模拟
为验证理论结果的正确性和控制措施的可行性,将使用Matlab和龙格-库塔方法模拟验证模型(1)的理论分析和控制措施的有效性.在模拟中时间以d为单位,特别地取定参数:Λh=4,Λv=34 000,μh=4.0×10-5.
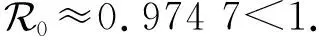
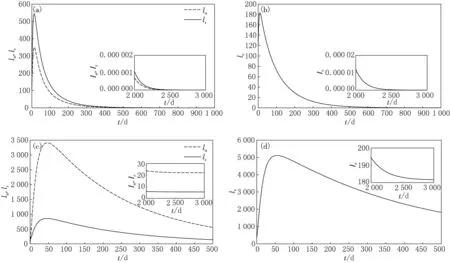
图1 模型(1)无病平衡点和地方病平衡点的稳定性
为讨论个人的自我保护意识和媒介控制措施对疟疾传播的影响,依次选取u为0,0.2,0.4和0.6.显然从图2(a)和(b)中可得无症状者和有症状者的数量随着人类的自我保护意识的增加而减少.因此可以通过增加易感者的个人防护意识以达到遏制疟疾传播的目的.类似地,随着媒介控制措施强度c的增加,染病者的总数量和染病蚊子的数量也将不断减少.数值模拟显示,减少蚊子的数量和加强个体的自我保护意识,对控制疟疾的传播起着至关重要的作用.
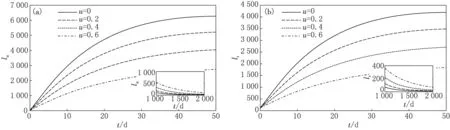
图2 个人的自我防护意识对疟疾传播的影响
