隔热屏辊压成型作业中压下系统力学特性
2021-07-16董钰峰阚彦淇
谢 苗,董钰峰,阚彦淇
(辽宁工程技术大学 机械工程学院,辽宁 阜新 123000)
0 引言
辊压机是由多个工作部件所组成的复杂工作系统,而在辊压机的组成部分中辊压工作的完成主要依靠压下系统[1-2].隔热屏辊压机的设计要求之一是实现对压下力、压下量的精确调节,而实现这两个参量精确调节的关键就是辊压机压下系统的结构强度和控制精度.但最终在辊压工作中所生产的隔热屏能否满足精度的要求不仅取决于所构成压下系统的各个部件的选择是否合理,还取决于所选部件的强度和刚度是否足够[3].辊压机在进行辊压工作时,其压下系统所控制的从动辊在垂直方向上的振动幅值大小会对工件的精度有直接的影响,因此对这种振动规律的研究十分必要.在建立模型过程中考虑到如果在研究这种垂直方向上的振动幅值时,只研究压下系统中的从动辊虽然也可以得出结果,但这种结果不够全面同时也不具有代表性.因此,在建立动力学模型时将主动辊即整个辊系考虑在内,建立主、从动辊垂直振动系统二自由度非线性动力学模型,并对该系统进行动力学方程的建立与推导以及幅频特性的研究.
王红霞[4]等对压下系统改造,增大了压下系统的传动力矩;关云华[5]对压下系统进行改进,解决了人工操作所导致的效率与精度问题;李威[6]等对六辊轧机机芯轴式分段支承辊的支反力进行了研究,对辊身直径的确定提供了理论支持;陈海波[7]运用Matlab中的Simulink模块与AMESim软件证实了压下系统改造方案的可行性;高瑞进[8]采用 ANSYS/LSDYNA软件进行了四辊轧机垂直振动的振动规律特征和固有特性研究;侯东晓[9]等进行了非线性动态轧制过程下冷轧机参激振动特性研究;LI H G[10]等在考虑了不连续条件下的诸多因素后,建立了轧机压下系统中的主传动部分的非线性间隙但自由度动力学模型;NIZIOL J[11]研究了轧制速度对辊子垂直方向振动的影响,并提出一种能够有效预测辊子在工作过程中沿垂直方向位移量的方法.
本文所研究的用于生产航空发动机隔热屏的辊压机来自于沈阳某航空发动机集团有限责任公司的隔热屏辊压机改进项目.本文在对原压下系统进行改进的基础上,对所建立的新型辊压机压下系统进行动力学特性分析及疲劳分析,以验证新型方案的可行性.
1 动力学模型建立
辊压机辊压工件时,主、从动辊与隔热屏工件间的阻尼和刚度均是非线性的,又考虑到主、从动辊部分在结构上的对称性,建立主、从动辊沿垂直方向上的非线性振动动力学模型,见图1.
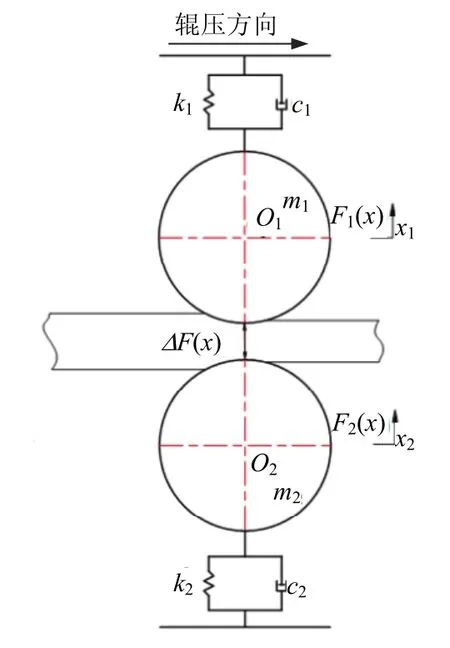
图1 主、从动辊振动模型Fig.1 vibration model of main and driven roller
图1中,m1和m2分别为从动辊部分等效质量和主动辊部分等效质量,kg;x1和x2分别为从动辊沿垂直方向上的位移和主动辊沿垂直方向上的位移,mm;F(1x)和F(2x)分别为从动辊部分与其他相连部件间的非线性力和主动辊部分与其他相连部件间的非线性力,MPa;k1和k2分别为从动辊与其他相连部分间的等效刚度和主动辊与其他相连部分间的等效刚度,N/mm;c1和c2分别为从动辊与其他相连部分间的等效非线性阻尼和主动辊与其他相连部分间的等效非线性阻尼,N⋅s/m;ΔF(x)为隔热屏工件的线性变形抗力,N.
又由于在实际辊压工况下存在系统间的润滑因素及隔热屏工件弹塑性变形等情况,因此在本节的动力学模型中引入 Vanderpol非线性阻尼振子(−c1+c2x2)x和 Duffing非 线 性 刚 度 振 子(k1+k2x2 )x,则有
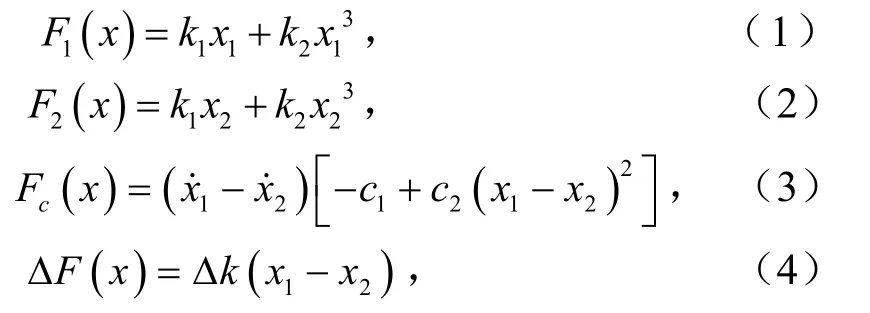
式中,F(cx)为非线性阻尼力,N.
2 动力学方程建立
在辊压机辊压过程中,主、从动辊系统不可避免的会受到来自系统外部的干扰力.因此,在本节所建立的动力学模型中加入一个作用在系统上的外部周期变化的干扰力F(x),其表达形式为

综合牛顿力学模型,主、从动辊垂直振动系统非线性动力学方程为
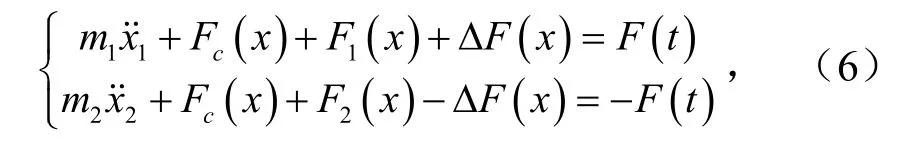
联立式(1)~式(4)和式(6)可得
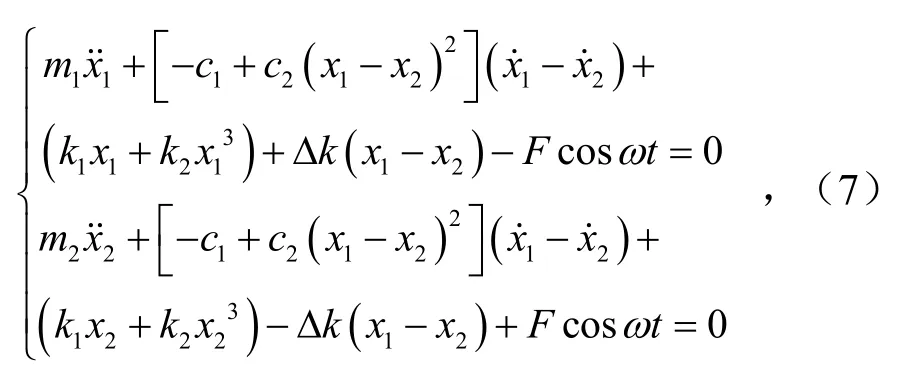
由于主、从动辊系统在设计结构上具有对称性,因此有:m1=m2,x1=x2.将其代入式(7)中进一步整理有
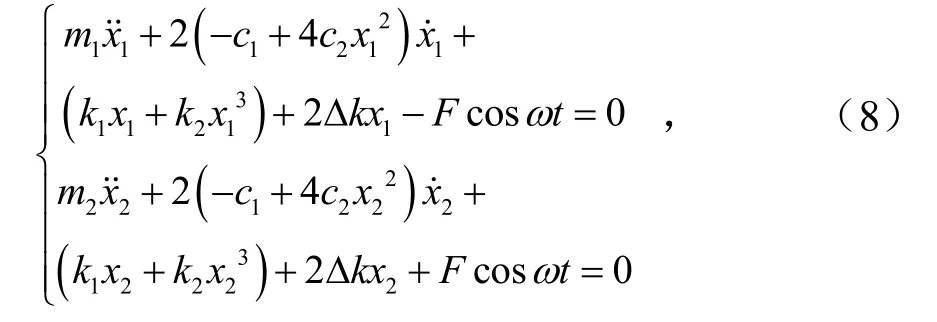
又因为式(8)中主、从动辊部分的2个方程在形式上完全相同,故只研究其中一个方程.本节选取从动辊部分动力学方程进行研究,并将其化为
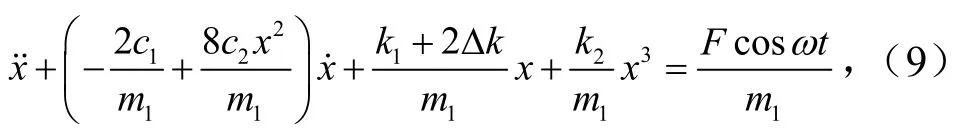
再分别将 − 2c1/m1=α,8c2/m1=β,k2/m1=γ,k1+2Δk/m1=ω02,F/m1=F'代入式(9)整理可得
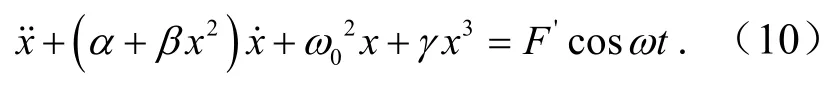
式(10)即为主、从动辊垂直振动系统的非线性动力学方程.
3 动力学方程求解
本节对建立的主、从动辊垂直振动系统非线性动力学方程进行求解,以得出可以进一步表现该振动系统特征的表达式,并为仿真提供理论方程.
首先将式(10)改写成
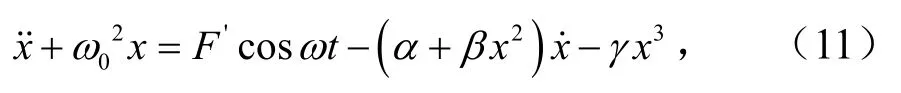
在此引入摄动法来求解式(11),根据摄动法将主、从动辊与隔热屏工件间的关于非线性刚度和阻尼部分以及系统外部干扰因素部分设为ε(一个无量纲小参数).则有
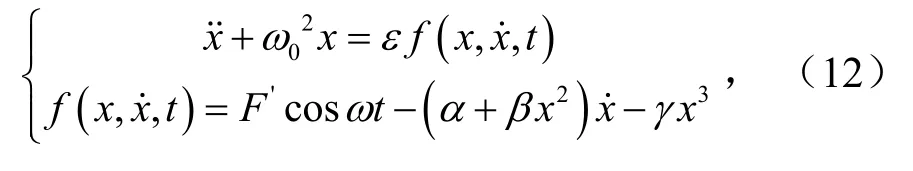
进一步,式(12)解的形式可设为
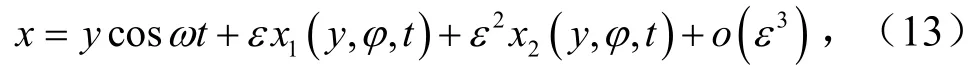
又有
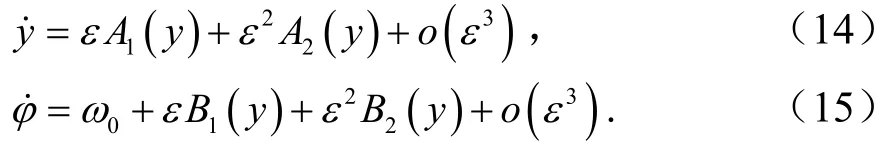
由此,对式(13)进行求导,并将其结果与式(14)和式(15)联立,推导可得
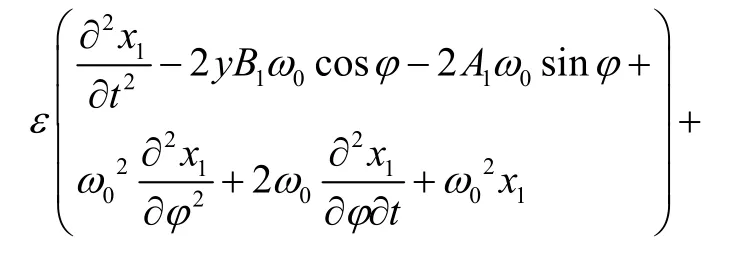
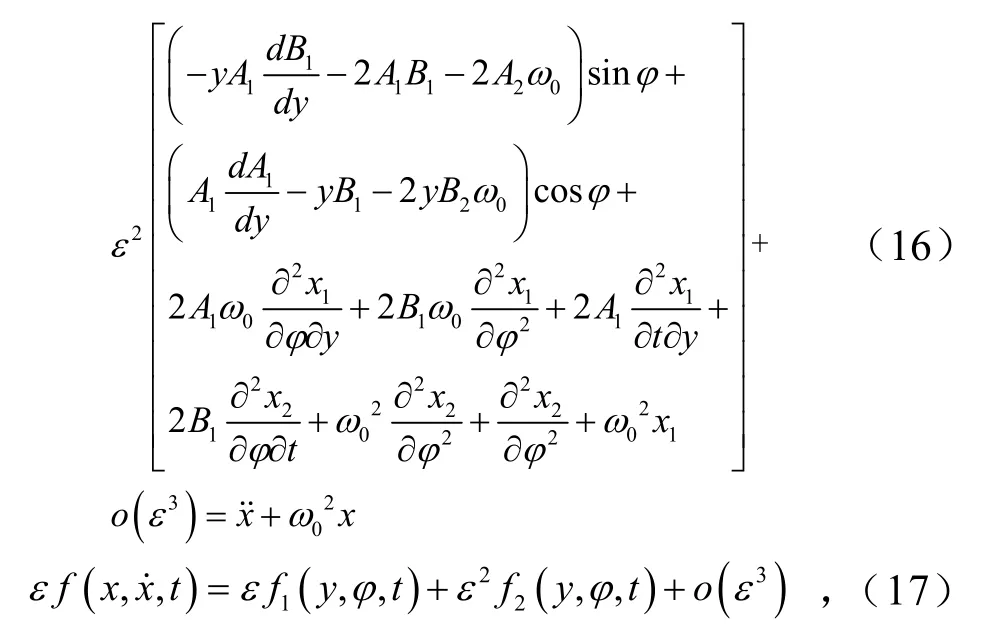
式(17)中,
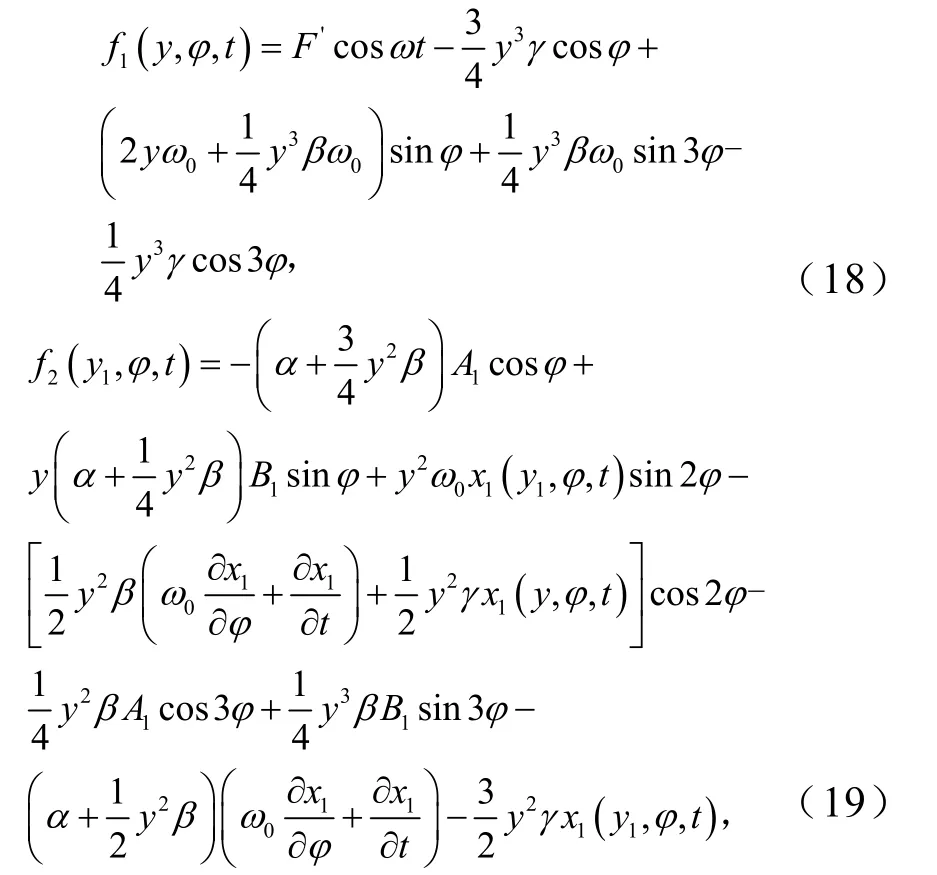
使式(16)与式(17)中ε项系数相等,再次整理得
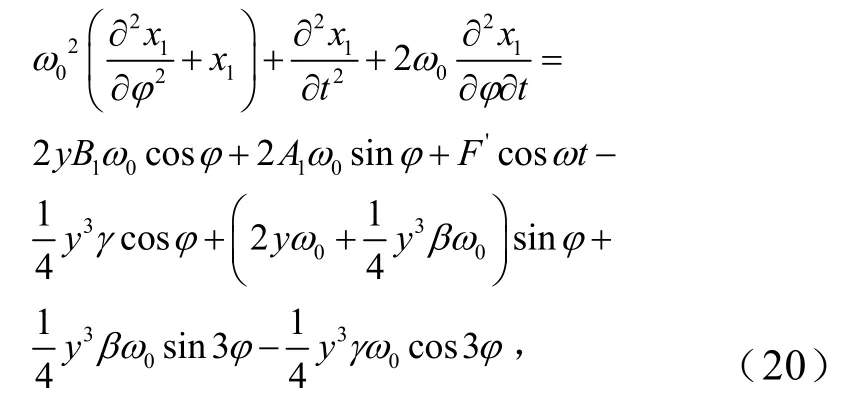
再使式(20)中sinϕ和cosϕ项前系数为0,有
联立式(20)与式(21)整理后得
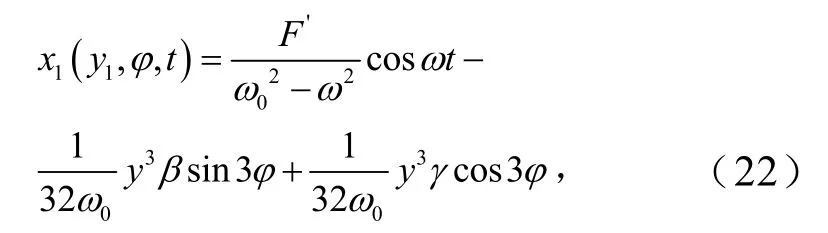
同理可得

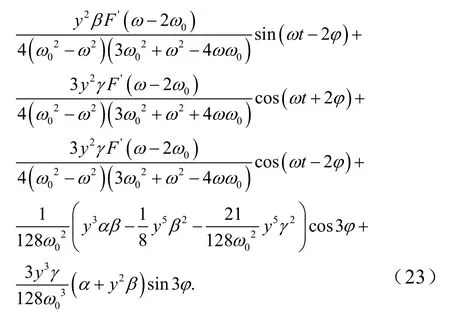
综上,可得出本节中所述的非线性动力学方程在收到系统外部干扰力条件下的解析近似解为

通过观察该主、从动辊垂直振动系统的非线性动力学求解过程和求解结果可知在非线性刚度、非线性阻尼和系统外部干扰力同时存在的情况下,动力学模型的求解过程和求解形式十分复杂.进一步对该求解结果进行分析,可知解中主要包含系统固有频率、系统外部干扰项、高次谐波项和耦合项.不难得知,当系统固有频率与因外部周期干扰力而产生的频率间存在某种数量关系时,主、从动辊垂直振动系统会有产生共振的可能.
4 仿真
本节用式(12)作为基础数学模型来进行动力学仿真,即
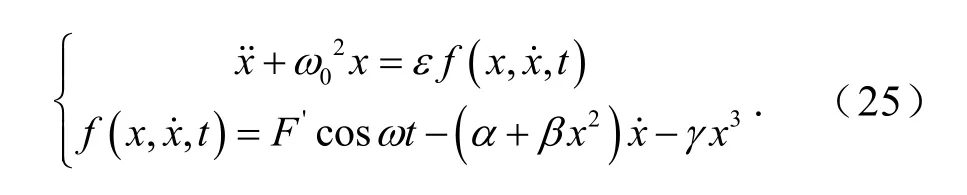
当作用在主、从动辊垂直振动系统上的来自系统外部干扰频率ω与系统固有频率0ω间存在整数倍关系时,有如下表达式
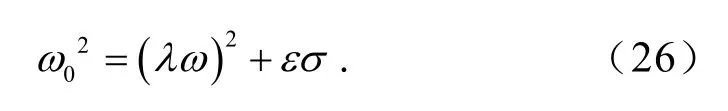
4.1 主共振动力学特性仿真分析
式(26)中,当λ=1时,主、从动辊垂直振动系统的固有频率与来自系统外部的干扰频率值无限接近几乎相等,这种情况下,主、从动辊垂直振动系统会产生主共振现象.
在此前提下,式(25)可改写成
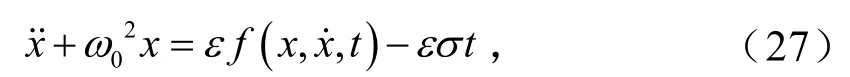
假设式(27)存在如下形式的解
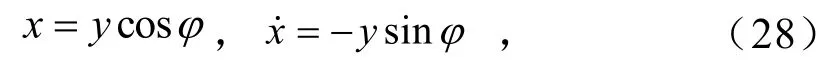
式中,ϕ=tω−θ.进一步求解可得
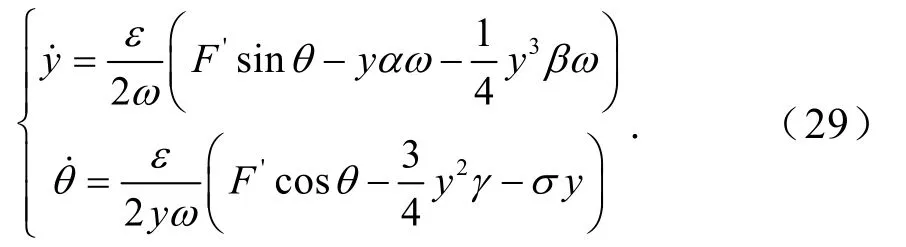
将式(26)代入式(29)整理可得主、从动辊垂直振动系统主共振动力学特性方程为
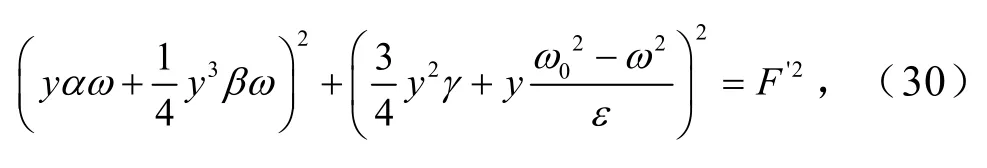
从式(30)的形式及内容可得知,与系统频率和振幅相关的因素为:阻尼系数α=−2c1/m1;非线性阻尼系数β= 8c2/m1;非线性刚度系数γ=k2/m1.
在此运用Matlab软件对主、从动辊垂直振动动力学模型进行幅频特性仿真分析,并进一步研究不同α、β和γ值对所建模型幅频特性关系的影响.其中,α和β为阻尼系数,γ为刚度系数.
所设计的新型辊压机上下辊系等效质量为m1=m2= 8 7kg.
参考相似结构[7-8]并结合辊压机实际工作环境,取:c1= 5 × 1 06N⋅s/ m ,c2= 2 × 1 06N⋅s/ m ,F'=1.5,ω0=1.5,ε=0.05.
具体仿真如下:
① 以刚度系数γ为变量的主从动辊垂直振动系统主共振幅频特性.
以刚度系数γ为变量,以.m文件编写式(30),并运用Matlab仿真,得出曲线见图2.
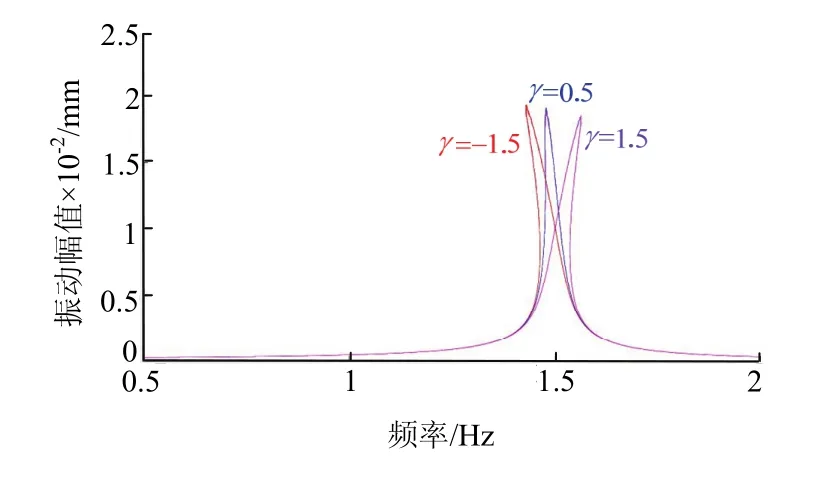
图2 不同刚度系数γ下主从动辊幅频特性Fig.2 amplitude frequency characteristic of main and driven roller at different stiffness coefficients γ
由图2可知,在3个不同的刚度系数下,主、从动辊垂直振动系统幅频特性曲线变化的规律基本相同,都是先处于平稳状态,随后随着外部干扰频率的逐渐增加振幅急剧增大之后又逐渐过渡到平稳状态.随着刚度系数的不断增大,曲线的幅值跳跃点逐渐向横坐标的正方向移动,最大振幅值越来越小.但3条曲线的幅值跳跃点均处于外部干扰频率值为1.4~1.6内.当刚度系数为-1.5时,幅值最大为2 × 1 0−2mm,当刚度系数为 1.5时,幅值最小为1.8 × 1 0−2mm.
② 以阻尼系数α为变量的主从动辊垂直振动系统主共振幅频特性.
以阻尼系数α为变量,以.m文件编写式(30),并运用Matlab仿真,得出曲线见图3.
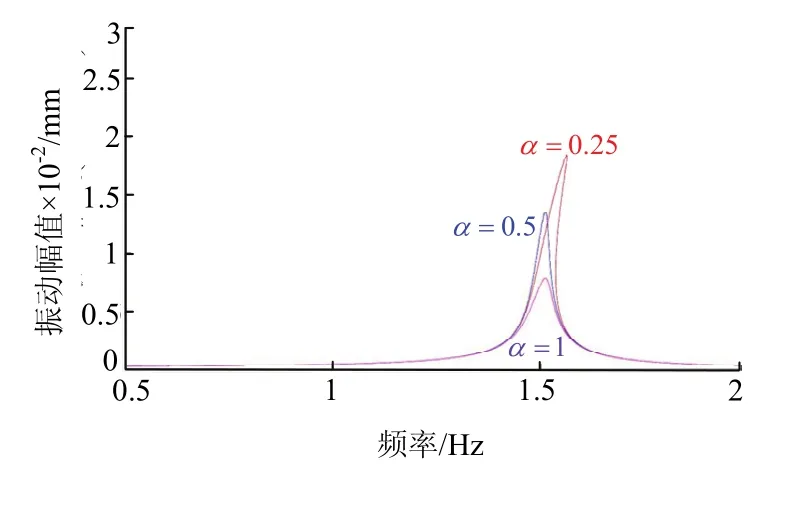
图3 不同阻尼系数α下主从动辊幅频特性Fig.3 amplitude frequency characteristic of main and driven roller at different damping coefficient α
由图3可知,在不同阻尼系数α下,主、从动辊系统幅频特性曲线走势几乎相同,但随着阻尼系数α的逐渐增大的过程中,主、从动辊系统的幅频特性曲线的幅值跳跃点逐渐向坐标左侧移动且振动峰值越来越小.从图3中观察得知,3条曲线在外部干扰频率为0.5~1.4和1.6~2的区间内几近重合.此时,主、从动辊系统的振动幅值最小,整个振动系统处于平稳状态;在外部干扰频率为1.5左右时,3条曲线均出现了跳跃现象.当阻尼系数α为0.25时,振动峰值最大为 2 × 1 0−2mm;当阻尼系数α为1时,振动峰值最小为 0.8 × 1 0−2mm.此时主、从动辊垂直振动系统可能会发生振荡现象,但随着外部干扰频率的继续增大,这种跳跃现象又逐渐消失,最后系统趋于平稳.
③ 以阻尼系数β为变量的主从动辊垂直振动系统主共振幅频特性.
以阻尼系数β为变量,以.m文件编写式(30),并运用Matlab仿真,得出曲线见图4.
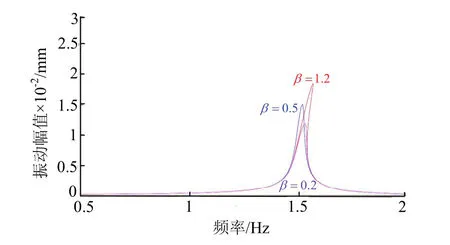
图4 不同阻尼系数β下主从动辊幅频特性Fig.4 amplitude frequency characteristic of main and driven roller at different damping coefficient β
由图4可知,在不同阻尼系数β下,主、从动辊系统幅频特性曲线变化情况与图3情况大致相同,但随着阻尼系数β的增大,主、从动辊垂直振动系统的振幅峰值越来越大.其中,当阻尼系数β为1.2时,系统振动峰值最大为1.9×10-2mm;当阻尼系数β为0.2时,系统振动峰值最小为1.2×10-2mm.
4.2 非主共振动力学特性仿真分析
当ω与0ω间的数量关系为0ω是ω的大于1的整数倍时,主、从动辊垂直振动系统会发生超谐波共振,这时有
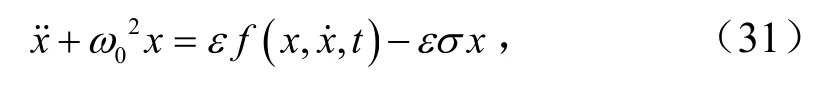
假设式(31)解的形式为
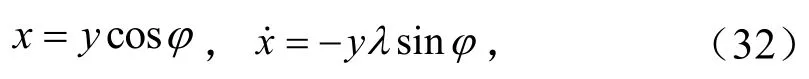
式中,ϕ=λωt−θ.
在此,取λ=2,则可得
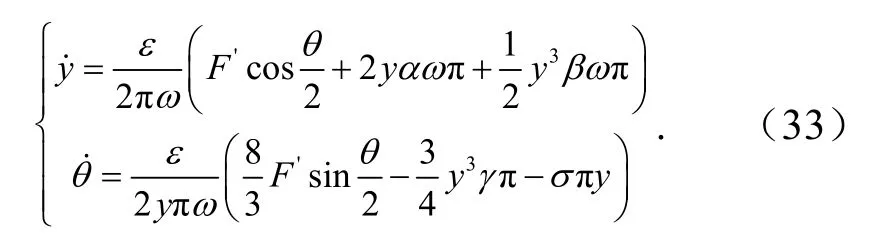
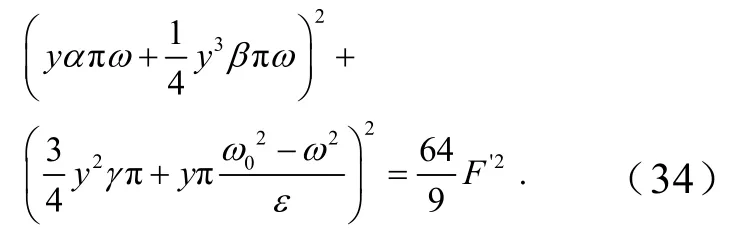
① 以刚度系数γ为变量的主从动辊垂直振动系统超谐波共振幅频特性.
将式(34)以.m文件编写,γ分别取-1.5、0.5、1.5,并运用Matlab仿真,结果见图5.

图5 不同刚度系数γ下主从动辊幅频特性Fig.5 amplitude frequency characteristic of main and driven roller at different stiffness coefficients γ
由图5可知,在刚度系数γ取不同值时,主、从动辊垂直振动系统幅频特性曲线变化的规律基本相同,均为先处于平稳状态,随后随着外部干扰频率的逐渐增加振幅急剧增大之后又逐渐过渡到平稳状态.另外,随着刚度系数的不断增大,曲线的幅值跳跃点逐渐向横坐标的正方向移动,最大振幅值越来越小,但3条曲线的幅值跳跃点均处于外部干扰频率值为0.75左右.当刚度系数γ为-1.5时跳跃点幅值最大为 2.9 × 1 0−2mm,刚度系数γ为1.5时跳跃点幅值最小为 2.6 × 1 0−2mm.
② 以阻尼系数α为变量的主从动辊垂直振动系统超谐波共振幅频特性.
将式(34)以.m文件编写,取α值分别为0.25、0.5、1,并运用Matlab仿真,结果见图6.
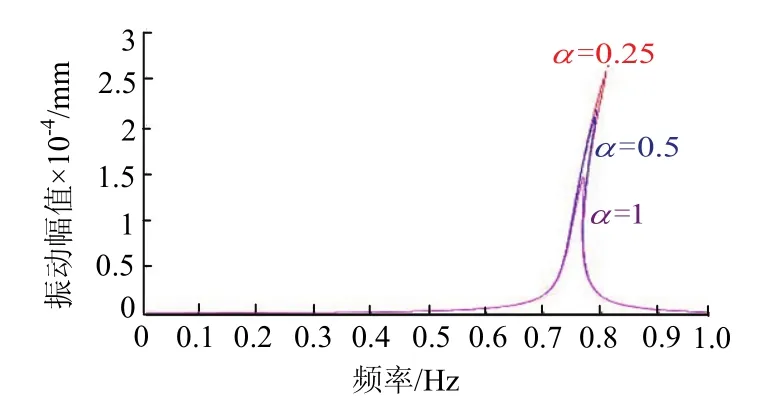
图6 不同阻尼系数α下主从动辊幅频特性Fig.6 amplitude frequency characteristic of main and driven roller at different damping coefficient α
由图6可知,在不同阻尼系数α下,主、从动辊系统幅频特性曲线走势几乎相同,但随着阻尼系数α的逐渐增大的过程中,主、从动辊系统的幅频特性曲线的幅值跳跃点逐渐向横坐标左侧移动且振动峰值越来越小.从图中观察得知,3条曲线在外部干扰频率为0~0.7和0.8~1的区间内几近重合,此时,主、从动辊系统的振动幅值最小,整个振动系统处于平稳状态;在外部干扰频率为0.75左右的区间内,3条曲线均出现了跳跃现象,当阻尼系数α为0.25时,振动峰值最大为 2.7 × 1 0−2mm;这种跳跃现象又逐渐消失,最后系统趋于平稳.
③ 以阻尼系数β为变量的主从动辊垂直振动系统超谐波共振幅频特性.
将式(34)以.m文件编写,取β值分别为1.2、0.5、0.2,并运用Matlab仿真,结果见图7.
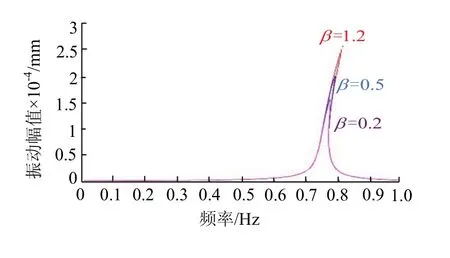
图7 不同阻尼系数β下主从动辊幅频特性Fig.7 amplitude frequency characteristic of main and driven roller at different damping coefficient β
由图7可知,在不同阻尼系数β下,主、从动辊系统幅频特性曲线变化情况与图6情况大致相同,但随着阻尼系数β的增大,主、从动辊垂直振动系统的振幅峰值越来越大.其中,当阻尼系数β为 1.2时,系统的振动峰值最大为 2.7 × 1 0−2mm;当阻尼系数β为0.2时,系统的振动峰值最小为 1.7 × 1 0−2mm.
5 结论
建立了辊压机主、从动辊统垂直振动系统2自由度非线性动力学模型,经过推导与求解得到了主、从动辊统垂直振动系统的幅频特性方程,研究了在主共振与非主共振情况下不同刚度与阻尼系数对该系统幅频特性的影响,经过对仿真图像分析得知:
(1)在主共振的情况下,刚度系数与阻尼系数的改变并不会影响主、从动辊垂直振动系统幅频特性曲线的整体变化趋势,但随着刚度系数和阻尼系数的变化,系统的幅频特性曲线也会随之发生一些变化.系统幅频特性曲线的跳跃点会随刚度系数的增大而逐渐向横坐标正方向移动,且跳跃点峰值随着这种变化从 2 ×10-2mm 至 1.8×10-2mm逐渐减小;系统幅频特性曲线的跳跃点会随阻尼系数α的增大而逐渐向横坐标负方向移动,且跳跃点峰值随着这种变化从2×10-2mm 至 0.8×10-2mm逐渐减小;系统幅频特性曲线的跳跃点会随阻尼系数β的增大而逐渐向横坐标正方向移动,且跳跃点峰值随着这种变化从1.2 × 1 0−2mm至 1.9 × 1 0−2mm逐渐增大.
(2)在超谐波共振的情况下,刚度系数与阻尼系数对主、从动辊垂直振动系统幅频特性曲线变化规律的影响与主共振的情况大致相同,但对系统幅值变化的影响与主共振时不同.系统幅频特性曲线的跳跃点峰值会随刚度系数的增大从 2.9×10-2mm 至2.6 × 1 0−2mm逐渐减小;系统幅频特性曲线的跳跃点峰值会随阻尼系数α的增大从 2.7×10-2mm 至1.5 × 1 0−2mm逐渐减小;系统幅频特性曲线的跳跃点峰值会随阻尼系数β的增大从 1.7×10-2mm 至2.7 × 1 0−2mm逐渐增大.
