基于分簇的WSN充电路径优化算法研究
2021-07-16安斯光
马 超,汪 伟,安斯光
(中国计量大学 机电工程学院,浙江 杭州 310018)
无线传感器网络(Wireless Sensor Network,WSN)由多个传感器节点组成,其具有感知、计算、存储等特点,已经广泛应用于军事、环境监测、交通管理等方面[1]。受节点体积的影响,传感器节点只能携带极小容量的电池,自身储存电量较少,所以传感器节点的电量有限问题已经成为WSN持续运行的瓶颈;这些节点通常放置于危险、复杂的环境下,人为进行维护变得困难。
解决上述问题的主要方式有:对网络进行分簇从而降低WSN数据传输能耗;通过无线充电的方式,采用移动充电车(Mobile Charging Vehicle,WCV)为传感器节点充电。
网络分簇是WSN减少自身能耗的一种重要方式,尤其是对中大型WSN,分簇能够减小簇内能量消耗。从WSN中选取传感器节点当选簇首节点,簇首节点承担主要能量消耗,簇首节点能够接收其他节点发送的数据并进行数据融合,减少数据发送量,通过这种方式达到降低网络平均能量消耗,延长网络存活时间的目的。文献[2]提出了WSN的一种经典分簇协议——LEACH协议。LEACH可以通过随机选择簇首与数据融合的方式减少网络通信能耗。在LEACH的基础上,文献[3]提出了LEACH-CC改进方案,对节点列出一个簇首当选次序,每个节点根据次序依次当选簇首节点。文献[4]基于LEACH提出能量均衡的改进算法,引入节点电量等因素进行分簇,从而优化簇首节点选择。文献[5]提出了多点改进的K-means算法,使用K-means算法依据传感器节点的位置进行划分,然后在簇内进行簇首选择。文献[6]提出了一种NSGA-Ⅱ多目标聚类算法,用该算法实现聚类分簇,根据用户的需求从中选择其中任意解。LEACH协议虽然能减小能耗,但是也有它的不足之处:簇首的选举是完全随机的,能量低的节点也可能当选为簇首,导致节点电量过早衰竭。
采用移动充电车给传感器节点进行充电是延长节点寿命的有效方式,如何对充电路径进行优化是一个关键问题。WSN中的充电规划问题与车辆路径问题类似,相关的优化算法有蚁群算法(Ant Colony Optimization,ACO)、模拟退火算法、遗传算法等[7-9]。蚁群算法采用分布式计算方法,具有全局搜索能力强、信息正反馈等特点,被广泛应用于该类问题[10-11]。文献[12]还提出了一种基于贪心策略的在线充电算法,每次选择距离充电车最近的节点充电。文献[13]基于K-means算法将网络划分为多个集群,提出用两个充电车相反方向移动进行充电。虽然以上研究能解决一定的充电路径问题,但是传感器节点的充电优先程度不同,WCV若不能及时到达需要充电的节点,节点可能会面临能量耗尽的问题。
在一次充电周期中,也需要考虑为不同数目的节点进行充电时,是否会影响充电效用,所以考虑设置充电阈值。有些文献提出为所有节点进行充电,此时不设阈值。文献[14]提出了给全部节点充电的充电方案,无线充电车一个充电行程为网络里所有节点充电,避免有传感器节点死亡。还有些文献提出选取一个阈值,为电量在阈值之下的节点进行充电,对部分节点进行充电。文献[15]提出了一种按需充电的充电方案,低于阈值的传感器节点提出充电请求,充电设备制定好充电次序之后依次为传感器充电。可是,设阈值是否能提高充电效用没有做出比较说明。
针对上述问题。本文将网络分簇和移动充电路径规划结合,提出基于分簇的WSN充电优化算法。本文主要有以下三点贡献。
1) 提出head-K-means分簇方法。将簇首选举机制和K-means算法结合,将距离相近的节点分配到同一个簇中,制定簇首轮换规则,用更加合理的簇首选择方式替代随机选举簇首。
2) 提出改进的蚁群算法(Modified Ant Colony Algorithm,MACO)。将传感器剩余电量这个影响因子添加到算法的转移规则中,与启发因子、信息素浓度共同决定蚂蚁下一节点的选择,从而优化WCV的充电路线,同时提高算法收敛速度。
3) 充电阈值仿真实验分析。通过实验结果分析不同充电阈值对充电效用的影响,并得出最佳充电阈值。
1 WSN网络模型
1.1 结构模型
在本文中采用如下所述结构模型:WSN部署在一个二维区域上,区域内随机分布n个规格相同的传感器节点,每个节点的位置是固定和已知的;基站位于WSN的中心位置,基站接收传感器节点发送的数据并决定所需充电的传感器节点,并将该信息发送给WCV;WCV从起始点出发,采取一对一的方式为节点充电,充电完成后再回到起始点。
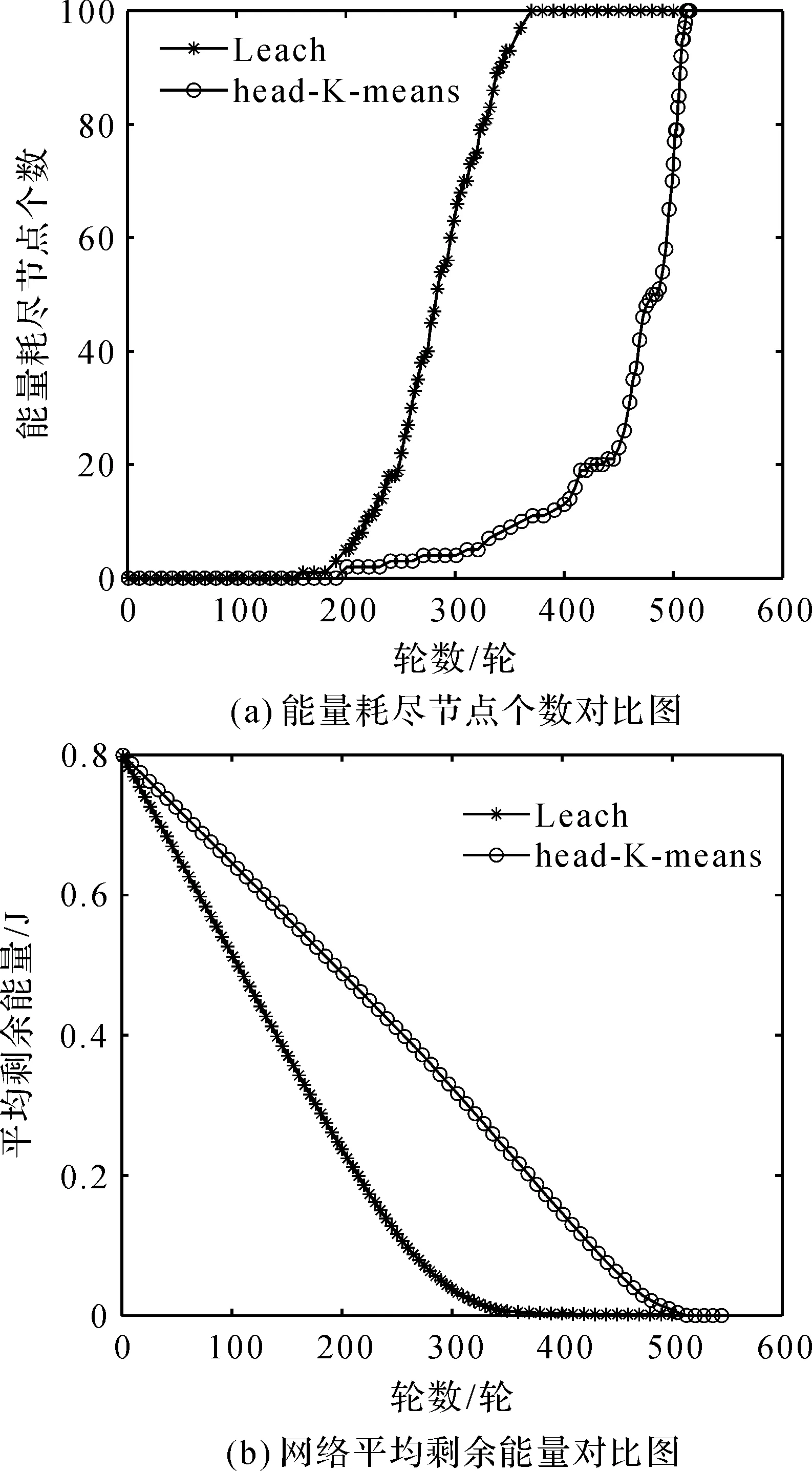
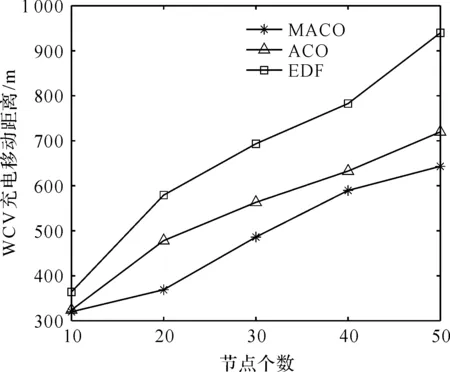
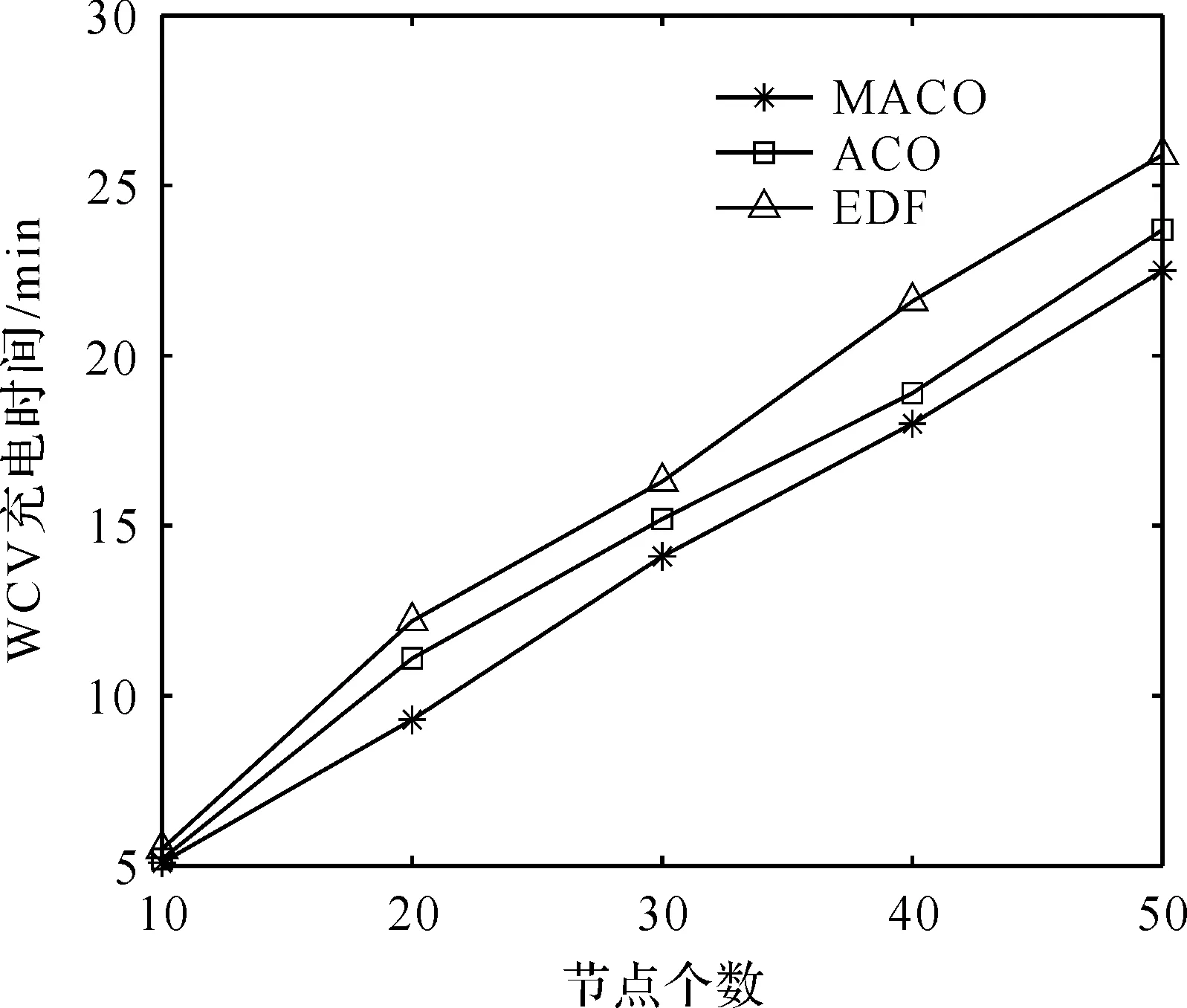
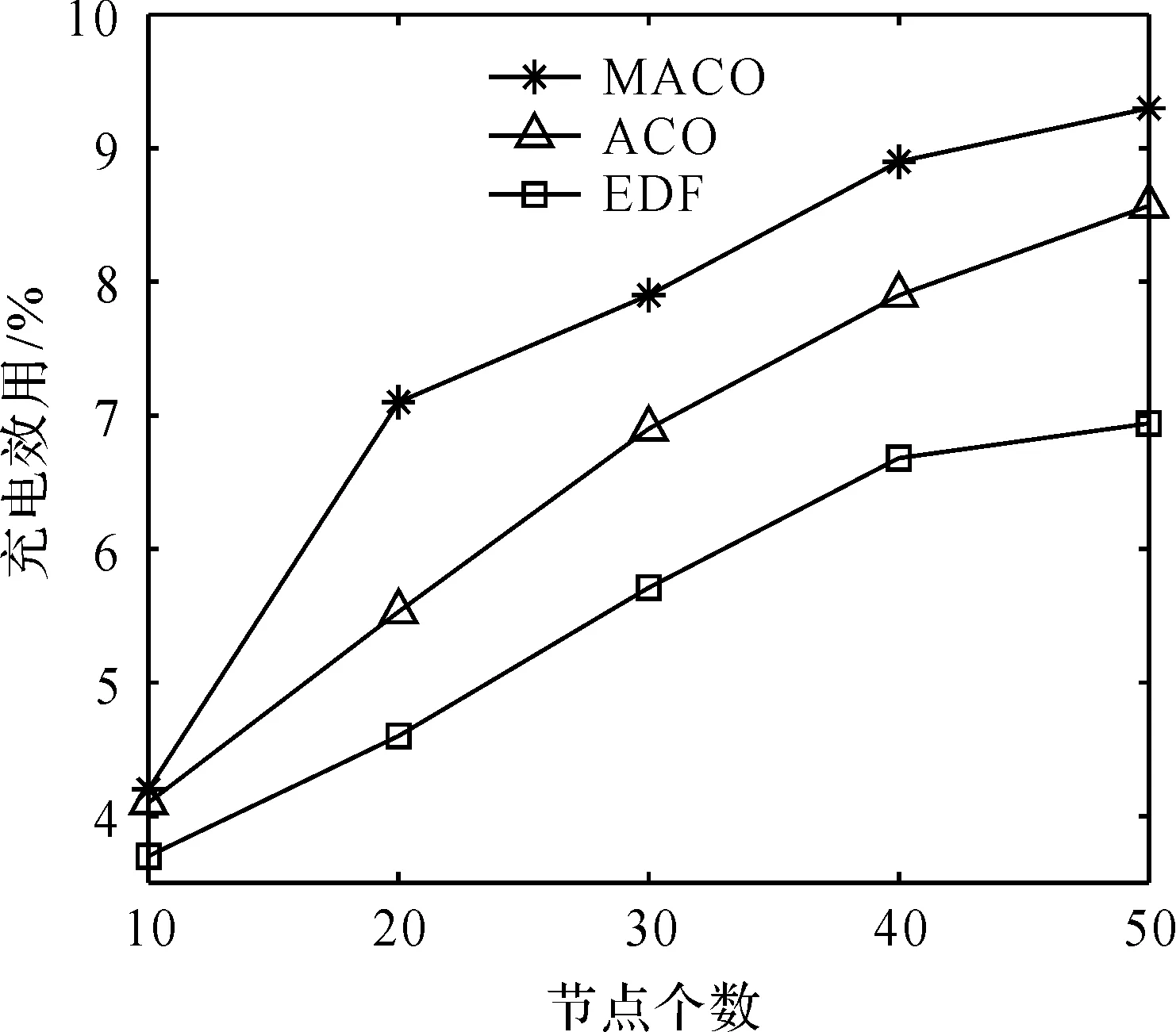
每个传感器节点都配备了相同容量的可无线充电电池,传感器具有相同的计算和通信级别,电池的最大容量用Emax表示。Ei表示节点i的当前电量,WCV行驶距离用L表示。需要充电的传感器设为集合G,G包含m个传感器,其中0 图1 网络结构示意图Figure 1 WSN structure diagram 传感器节点的能耗主要产生于数据的发送,特别是在数据量比较大的情况下,节点长期工作在数据的发送和收集状态。每个传感器节点监测周围环境并生成数据,并将自身收集到的数据发送给簇首节点。 在本文的WSN中,假设所有节点的电池容量完全相同,但是节点的初始电量不同,节点能够监测自身电池的剩余电量。由于本文考虑到网络分簇,簇首节点和普通节点的能耗不同,为了便于计算,使用文献[16]中的能量损耗模型: 在d距离下传输abit数据所消耗的能量如式(1)。 (1) 其中d0用式(2)表示: (2) 接收abit所需能耗由式(3)表示: ERx(a)=ERx_elec(a)=aEelec。 (3) 式(3)中,a为节点的数据监测量。Eelec为节点发送或接受1 bit所需要的能量消耗;εfs为自由空间时功率放大器的消耗参数;εtrg为多路径传输时功率放大器的消耗参数。因为接收端不需要进行信号放大,所以接收端没有放大器的能耗。 由于簇首节点需要对数据进行融合,在进行数据融合时也需要消耗一定的能量。假设融合1 bit数据所消耗的能量记为Ed。则簇首节点接收nbit数据之后,对nbit数据进行融合,然后发送给基站。 簇首的能耗表达式如式(4): E=ETx+ERx+n×Ed (4) 选取充电路径长度和WCV充电一周所需要的时间以及充电效用作为评价指标。 1) 目标函数 最终的目标是得到充电路径,所以优化充电路径就是本文的主要目标。目标函数用WCV的移动距离来表示,即WCV完成一周充电所移动的距离,如式(5): L(x)=dist(start,x[1])+ (5) 式(5)中,L(x)为路径长度,start为充电车的起点,用x代表每个传感器节点,x[i]为WCV第i个到达的传感器节点,dist表示距离。 为了避免在充电过程中出现节点死亡,加入一个约束条件,WCV在到达充电节点之前要保证该节点的剩余电量大于0,所以节点i的电量Ei要保证满足式(6),即WCV到达该节点之前,传感器节点剩余电量能维持正常工作。 (6) 式(6)中,Li是WCV到达节点i所需要走的路径长度,τj为WCV给节点j的充电时间。s为节点电量平均消耗速度。如果不满足该约束条件,则添加一个惩罚函数。 所以,此时的目标函数如式(7): (7) 式(7)中,p(x)为惩罚函数,M为惩罚因子,c为常数,惩罚因子设置为远大于L(x)的数,如果得到的充电路径中不满足约束条件(6),则c=1;否则c=0。 2) 充电时间 充电时间用T来表示,充电时间由两部分构成,一个是WCV充电时移动所需要的时间,另一个是为传感器节点充电所需要的时间,如式(8): (8) 式(8)中,τi为WCV在节点i的充电时间。 3) 充电效用 WCV充电效用其含义是:WCV向节点补充的能量与其消耗的总能量的比值。如式(9): (9) 式(9)中,用Ei表示节点i的剩余电量。Eroute代表WCV充电一周移动消耗的电量。 在充电之前首先要对网络进行分簇。本文提出新簇首选举机制的head-K-means算法进行分簇。在该算法中,网络分簇分成三个步骤:1) K-means算法进行区域划分;2) 簇首选择;3) 簇首轮换。 K-means算法是一种基于距离的聚类算法,因其算法简洁、方便高效的特点使得它成为使用最广泛的聚类方法。将距离作为相似度程度的评价标准,即认为节点之间的距离越近,他们的相似度就越大,相似度的接近程度决定了节点能否分到相同的簇中。 首先将数据预分为k组,然后随机选取k个对象作为初始的聚类中心;计算每个对象与各个聚类中心之间的距离,然后每个对象分配给距离它最近的聚类中心,聚类中心以及分配给它的对象就组成了一个聚类;每分配一个对象,根据类中现有的对象对聚类中心重新进行计算;这个过程将不断重复直到满足没有聚类中心再发生变化。 在分簇过程中,簇首的选举是尤其重要的。在有些分簇算法中,簇首的选举是随机的,这样会加大节点之间电量的不均衡。K-means算法一般只是计算出簇的范围,将质心作为整个簇的中心,这样虽然簇首节点到簇内子节点的平均距离是最短的,但是簇首节点的负担很重,大大增加了中心节点的能耗。所以需要设计一种动态选取簇首的方法。 本文综合考虑了节点剩余电量、节点位置、当选簇首次数等因素,动态选择最优的节点当选簇首,并且在完成一轮数据收集之后,轮换簇首节点。簇首选择方法如式(10),C最大的节点成为簇首。 (10) 式(10)中,Ei表示节点i的剩余电量,Eave(m)表示第m个簇的平均电量。Ai表示节点当过簇首的次数。D(i)表示簇首节点到i节点的距离,Dmax(m)表示第m个簇内子节点与簇首节点的最大距离,D(i)to_base表示节点i到基站的距离。α,β,γ是三个影响因子,在设定的时候遵循一定的原则,当网络整体电量较低时,α的值设置较大;当更看重网络节点间相互距离时,β此时需要占主导地位;当需要考虑节点当选簇首次数的时候,γ设置成为较大的值。 head-K-means算法的具体步骤如下。 步骤1 取随机k个位置当选最开始的聚类中心。 步骤2 网络中所有节点通过计算与聚类中心的距离,并加入最近的聚类中心所在的簇中,直到所有的节点找到自己的簇。 步骤3 根据节点位置,计算所生成的k个簇的中心坐标,得到簇中心位置。 步骤4 当簇心位置不再变化时,算法结束,此时得到的分簇结果就是期望的结果。否则继续迭代,重复执行步骤二,直到簇心位置不再变化。 步骤5 根据公式(10)选举簇首。 步骤6 若发送完一轮数据,重复以上步骤。 在本文中传感器节点的电量健康状况是十分重要的。传统的蚁群算法只考虑了信息素浓度和启发路径函数两个方面来确定下一节点的选择,却忽视了节点剩余电量的影响,从而在充电过程中出现节点死亡的情况。 1) 修改的转移概率 转移概率是蚁群算法的核心,蚂蚁会根据转移概率来选择下一个要访问的传感器节点,在蚁群算法的转移概率中添加节点当前电量,如式(11): (11) 式(11)中,τij表示节点i与节点j连接路径上的信息素浓度;α为信息素重要程度因子,其值越大,表示信息素浓度在选择下一充电节点中起的作用越大。β为启发信息重要程度因子,其值越大,表示启发信息在转移中的作用越大,即蚂蚁就会以较大的概率转移到距离较近的节点。Ej是传感器节点j的剩余电量,c为常数,γ为电量因素重要程度因子,当网络节点电量处于较低水平时,γ的值要相应增大。allowk表示G中还没有被充电的传感器节点集合。式中启发信息ηij如式(12): (12) 式(12)中,dij表示节点i到节点j的距离。由于下一个节点选择是一个概率问题,蚂蚁依然有可能向距离自身较远或者信息素浓度较低的路线移动。 2) 信息素更新 在所有蚂蚁完成一次路径搜索之后,节点之间蚂蚁走过的路径进行信息素更新,如式(13): (13) 3) 算法终止条件 在蚁群算法中,完成一次迭代的标志是所有蚂蚁都完成路径搜索,所以开始时要确定蚂蚁的数量,还要设置最大迭代次数。当所有蚂蚁都完成一次路径搜索,迭代次数加1,直到达到最大迭代次数条件时,算法结束,此时得到的收敛路径即为最佳路径,输出该路径长度,同时把该条路径保存。 步骤1 初始化参数:节点位置、蚂蚁个数m、最大迭代次数Nmax、蚂蚁位置。 步骤2 迭代次数N=N+1。 步骤3k=k+1。 步骤4 计算节点的剩余工作时间、蚂蚁跟各节点之间的距离。 步骤5 根据公式(11)选择下一充电节点。 步骤6 更新禁忌表,重复步骤5,直到所有待充电节点完成充电。 步骤7 若k 步骤8 进行信息素更新,比较所有蚂蚁最短路径并记录。 步骤9 若N 基于head-K-means分簇的WSN充电路径优化算法完整的流程图如图2。 图2 算法流程图Figure 2 Algorithm flow chart 在Matlab环境下分别对分簇算法以及分簇后MACO优化算法进行仿真,并对实验结果进行分析。实验参数设置如表1。 表1 仿真参数设置 在后面三小节里分别对分簇算法、充电优化算法以及充电效用进行实验仿真,并对结果进行分析。 针对现有文献中提到的全部节点充电和部分节点充电,哪种方式更能够提高充电效用问题。用本文基于分簇的充电路径优化算法对不同阈值下充电效用进行比较分析,得出充电效用与设置阈值之间是否存在关系。 为了验证本文head-K-means分簇算法的有效性,与LEACH分簇算法进行比较,比较两种算法在不进行充电情况下,出现节点死亡的时间、网络持续运行时间。图3为head-K-means算法和LEACH算法两个方面的对比图。 图3(a)为能量耗尽节点个数对比图。横坐标为网络运行轮数,纵坐标为能量耗尽节点个数,从图中可以看出,head-K-means算法中能量耗尽的节点出现的轮数明显后移。图3(b)为网络剩余能量对比图。在初期两种算法的能耗接近,但是随着实验轮数不断增加,使用LEACH算法网络平均剩余能量下降速度更快。使用LEACH算法时,在大概350轮时网络的平均剩余能量降为0;而使用本文算法时,在500轮时网络的平均剩余能量才降为0,所以能得出head-K-means算法的能耗比LEACH算法更小。 图3 分簇算法对比图Figure 3 Comparison diagram of clustering algorithm 表2为两种分簇算法,出现节点死亡和全部节点死亡的轮数。LEACH分簇算法第一个死亡节点大概出现在150轮,而本文head-K-means算法第一个死亡节点大概出现在200轮,推迟了33%左右;在大概350轮时网络全部节点死亡,而本文算法出现在510轮,推迟了大概46%。 表2 分簇算法对比 综上所述,与LEACH算法相比,本文提出的head-K-means分簇算法更能够均衡网络的能耗,延长网络工作时间。 使用head-K-means分簇算法后,采用MACO算法进行充电。从实验中选取了一个WCV移动路径图,如图4。图中中心信号塔为基站,五角星为每个簇的簇首节点,其他不同形状的符号代表不同簇中的节点。WCV的起始点为(0,0)点。 为了验证MACO算法的有效性,与两种经典充电调度算法进行对比:ACO算法和EDF算法。ACO算法为原始的蚁群算法。EDF算法称为最早截止优先算法,根据节点电量所能维持的工作时间动态分配优先级,工作时间越短,优先级越高;工作时间越长,优先级越低。 用本文的MACO算法与ACO算法以及EDF算法进行比较,从全部节点中选取电量最低的10~50节点构成需要充电的传感器集合G。每个实验分别进行30次并取平均值。 全部实验数据平均值如表3。 表3 三种算法实验数据对比 表4为MACO算法和ACO算法收敛速度对比,从中可以看出两者都有较快的收敛速度,并且MACO收敛速度更快。 表4 算法收敛速度对比 图5为WCV充电路径长度对比图,从图中可以看到本文的MACO算法明显优于其他两种,而且随着待充电节点数目的增加,优势更加明显。 图5 路径长度对比图Figure 5 Comparison chart of path length 图6为WCV充电一周所需要的时间对比图,从中可以看出,当待充电节点个数较少时,如G中有10个节点时,三种方法WCV所用的时间大小比较接近,随着网络规模的增大,MACO算法更优于ACO算法,相比于EDF算法优势更加明显。 图6 WCV充电一轮时间对比图Figure 6 Comparison chart of WCV charging round time 图7为网络充电效用对比图,同样在G中只有10个节点时,三种算法的差距不大,随着节点数量的增多,MACO算法的优势更加明显,即MACO算法的WCV充电效用更高。 图7 充电效用对比图Figure 7 Comparison chart of charging utility 随着电量阈值增大,需要充电的节点会增多,充电效用更能反映能量利用率。为了分析不同充电阈值对充电效用影响,本文通过仿真实验对比不同阈值下充电效用。进行多组仿真实验,每组进行30次实验,结果取平均值,如图8。 取阈值区间30%~90%以及不设阈值进行对比,给电量处于阈值之下的节点进行充电。分析图8可以得到,当阈值过小或者阈值过大都不能得到最佳的充电效用,最佳充电效用出现在53%~55%,从而可以得出充电阈值的大小能够影响充电效用。 图8 不同阈值下充电效用对比图Figure 8 Comparison chart of charging utility under different thresholds 本文提出了一种基于分簇的WSN充电路径优化算法,并通过实验仿真验证了算法的有效性。首先提出新簇首选择机制的head-K-means分簇算法,与LEACH算法相比,第一个死亡节点出现时间推迟了33%左右;全部节点死亡时间推迟了大概46%。提出改进的蚁群算法对分簇后的WSN进行充电路径优化研究,把节点剩余电量加入到蚂蚁概率转移规则中,仿真结果表明,MACO优化算法相比于ACO算法和EDF算法在充电车充电移动距离、充电时间以及充电效用方面都有一定的优势。最后对比了不同充电阈值下充电效用,实验表明充电阈值能够影响充电效用,在本文实验环境下53%~55%左右时充电效用最大。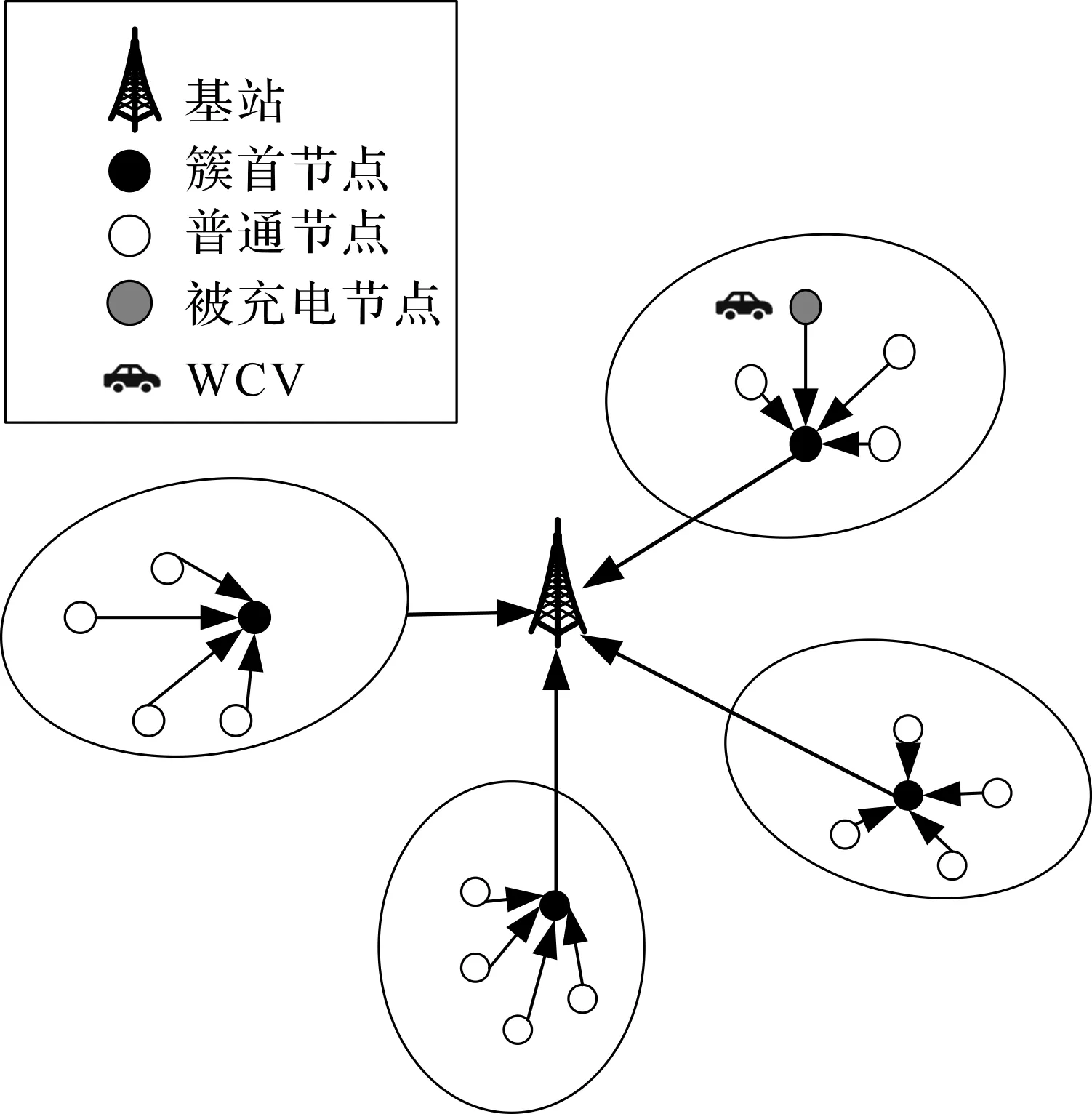
1.2 能耗模型
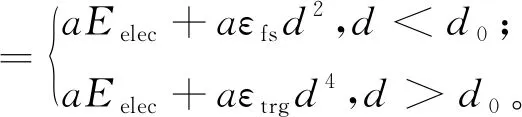
1.3 评价指标
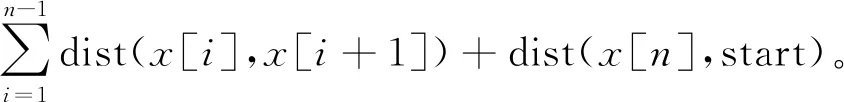
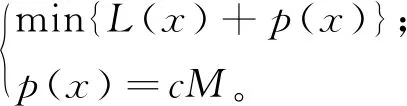
2 分簇算法
2.1 K-means算法
2.2 簇首选举机制
2.3 head-K-means算法实现步骤
3 充电路径优化算法
3.1 改进的蚁群算法
3.2 改进的蚁群算法实现步骤
3.3 基于分簇的充电路径算法流程图

4 仿真及结果分析

4.1 分簇算法仿真及结果分析

4.2 充电路径优化算法仿真及结果分析


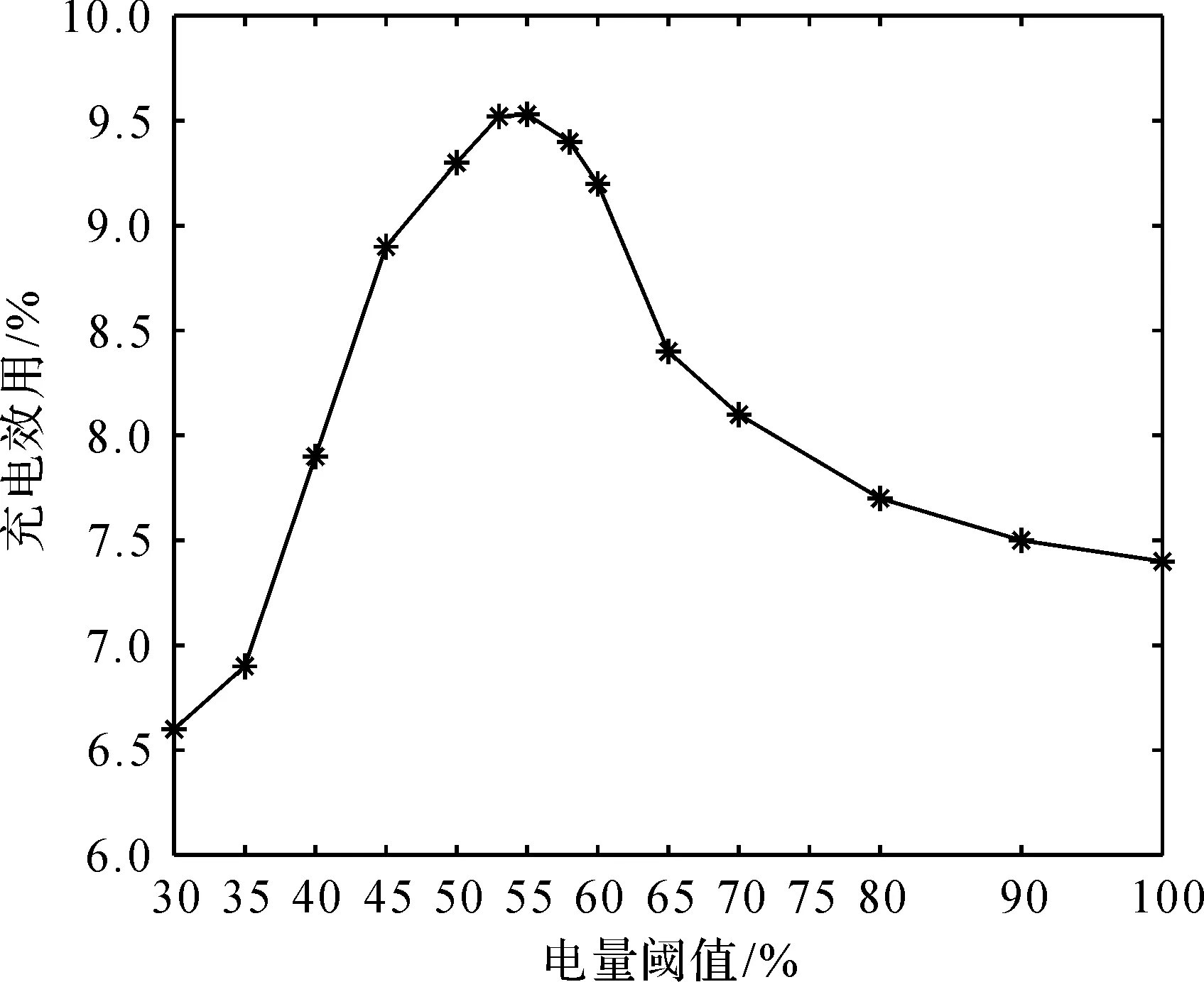
4.3 不同阈值下充电效用对比
5 结 语
