椭圆发热体倾角对方腔内自然对流的影响研究

韩 田，武 祥，宋克伟

(兰州交通大学 机电工程学院&铁道车辆热工教育部重点实验室，兰州 730070)

自然对流是流体内部因冷热流体间密度差而自发形成的对流，广泛存在于电子元件冷却、供暖、室内气候以及地球大气环境等领域，国内外学者针对自然对流开展了广泛的研究.设备舱内电子元器件不使用风扇强制冷却时的散热属于有内热源的封闭腔内自然对流换热问题.促进封闭腔内的自然对流，对于电子元器件的寿命和可靠性具有重要意义.Girgis等[1]使用数值和实验方法研究了封闭腔的长宽比对自然对流的影响，总结了不同长宽比下，Nu数关于θ的变化规律.李世武等[2]运用Fluent有限元软件对Girgis等[1]的实验数据进行了验证，计算结果和实验数据一致.任嘉友等[3]对高方腔内自然对流问题进行了数值研究，结果表明，在方腔顶部区域,冷板侧的传热相对更强,而在贴近底板区域,热板侧的传热相对更强.

含有不同形状内热源的腔内自然对流模型更加贴近工程实际.在科学研究中常常将热源的形状进行简化，常见的内热源形状包括圆形、方形、椭圆形、条形等[4-9].Elsherbiny等[4]对含方形发热体的方腔内自然对流问题进行了数值研究，结果表明方腔下壁面的两个边角附近的换热较好.Cho等[5]对竖直布置的两个椭圆的纵横比对换热的影响进行了数值研究，结果表明低Ra数时Nu数随着长短轴之比的增加而增加.Park等[6]研究了内置圆柱的半径和方腔的倾斜角度对方腔内自然对流的综合影响，结果表明方腔内换热会受到半径、倾斜角度和Ra数的综合影响.

此外，内热源在封闭腔内的位置和角度也会对腔内的流场分布产生影响，进而影响换热[10-18].Cianfrini[10]研究了双圆形发热体在充满水的矩形方腔内的自然对流换热问题，结果表明，发热体间距对上方发热体的影响更为明显，增大间距可以增强方腔上壁面换热，但圆形发热体与上壁面间距较小时，对上壁面的换热提升较为有限.Souayeh[11]对三维圆柱的倾斜角度对方腔内的流动换热影响进行了研究，结果表明，Ra数为106、倾角为90°时，圆柱和壁面的Nu数均达到最佳.Liao等[18]在Ra=105时，对椭圆形发热体倾斜角对换热的影响进行了研究，结果表明：椭圆形发热体短轴与长轴之比在0.25～1之间时，方腔壁面平均Nu在倾角90°时最大.

综上所述，目前关于内置椭圆形发热体方腔内自然对流换热的研究还不够完善，有必要对不同Ra数下、内置不同倾角椭圆形发热体方腔内的自然对流问题进行深入探讨.本文在Ra=103～106范围内，研究了内置不同倾角椭圆形发热体方腔内的自然对流换热问题，并与等周长的圆形发热体对方腔内自然对流的影响进行了对比，得到了方腔内流场、温度场以及Nu数随倾角和Ra数的变化规律.

1 数值方法

1.1 物理模型

内置椭圆形发热体的二维方腔物理模型如图1所示.方腔边长为L，温度为TCOLD；椭圆形发热体为高温热源，表面温度为THOT；重力加速度方向为Y轴负方向.椭圆形发热体长半轴为a，短半轴为b且a/b=2，椭圆周长与半径为0.2L圆的周长相等；椭圆倾角θ为长半轴a与X轴正方向的夹角，φ为椭圆发热体表面相对X轴方位角.

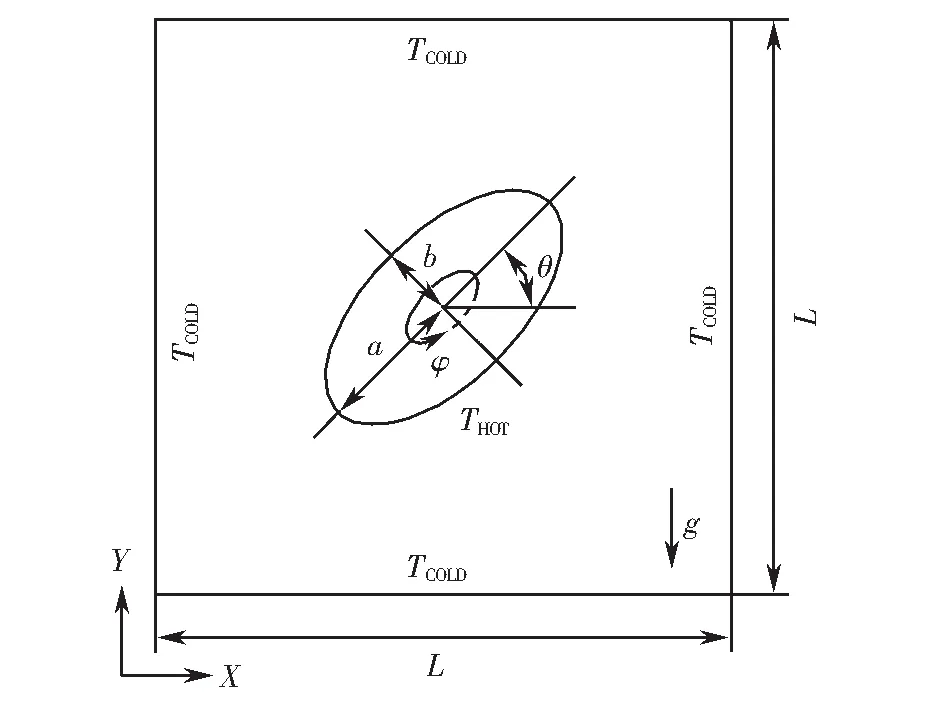
图1 模型示意图Fig.1 Diagram of the model

1.2 控制方程与边界条件

连续性方程：

(1)

动量方程：

(2)

能量方程：

(3)

局部Nu：

(4)

平均Nu：

(5)

Ra数：

(6)

介质为空气，假设符合Boussinesq假设，物性参数参考温度为Tref=(THOT+TCOLD)/2=293 K，忽略辐射对换热的影响.

1.3 网格独立性及结果验证

采用ICEM进行网格划分，网格如图2所示.在方腔壁面、椭圆形发热体表面附近网格加密处理.以上方程采用Fluent求解器、SIMPLE算法，求解精度为双精度，压力选择Body-Force Weighted格式，动量方程、能量方程选择二阶迎风格式.

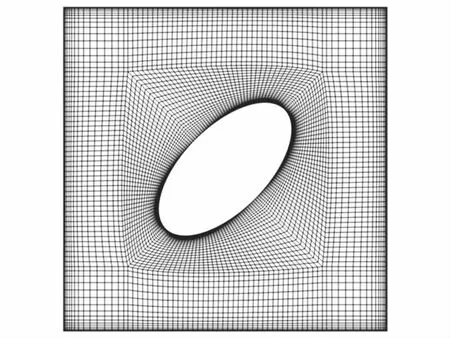
图2 网格划分示意图Fig.2 Schematic diagram of the mesh

为保证计算结果的准确性，针对Ra=106、θ=45°时的模型进行了数值解的网格独立性验证.如表1所示，网格数量分别为150×150、200×200、250×250、300×300，细网格数量是粗网格的4倍.不同网格计算得到的Nu间的误差最大不超过0.2%，文中所有结果均采用数量为250×250的网格.

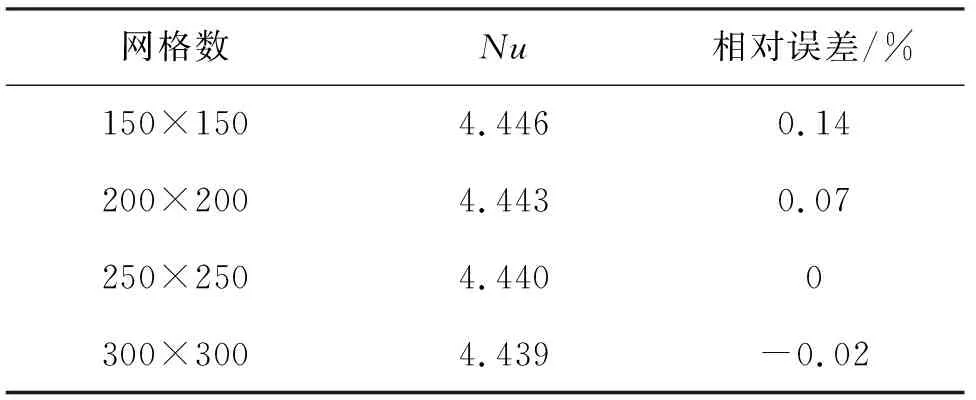
表1 网格独立性考核Tab.1 Grid dependency test results

为验证数值方法和结果的正确性，图3(a)为椭圆不同倾角下方腔壁面Nu与文献[18]中数据的对比，Nu相对误差最大不超过1%.图3(b)为倾斜角度为0°时方腔壁面Nulocal分布对比图，可见计算结果与文献基本一致.因此，本文的计算结果具有可靠性.

图3 本文与文献数据对比Fig.3 Comparisons of present results with literature

2 结果与讨论

2.1 Ra、θ对速度场、温度场的影响

不同Ra、倾角θ下的速度场如图4所示.随着Ra的增大，对流增强、速度显著增加，图4(a)、(b)、(c)、(d)对应的速度标尺分别为0.006 67 m/s、0.025 m/s、0.076 9 m/s、0.118 m/s.由于发热体的温度较高，发热体附近的流体被加热后向方腔上部聚集，而壁面附近的流体温度较低，向方腔下部聚集.因此，方腔左壁面与发热体之间的涡为逆时针，右壁面与发热体之间的涡为顺时针.θ=0°、90°时，模型左右对称，不同Ra下的速度场也对称分布.倾角θ较小时，在方腔内左右两侧分别有两个涡，随着θ的增加，方腔内四个顶角区域各有一个涡.随着倾角的增大方腔左右两侧的通流区域宽度逐渐增大，方腔内左右两侧间的涡逐渐合并.因此，当θ=60°～90°时，不同Ra下方腔左右两侧都只存在一个涡.在相同倾角下，浮升力随着Ra的增大而增强，方腔上部速度逐渐增大，方腔下部涡旋上升与上部涡旋逐渐合并，涡旋完全合并对应的倾角随着Ra的增加逐渐减小.

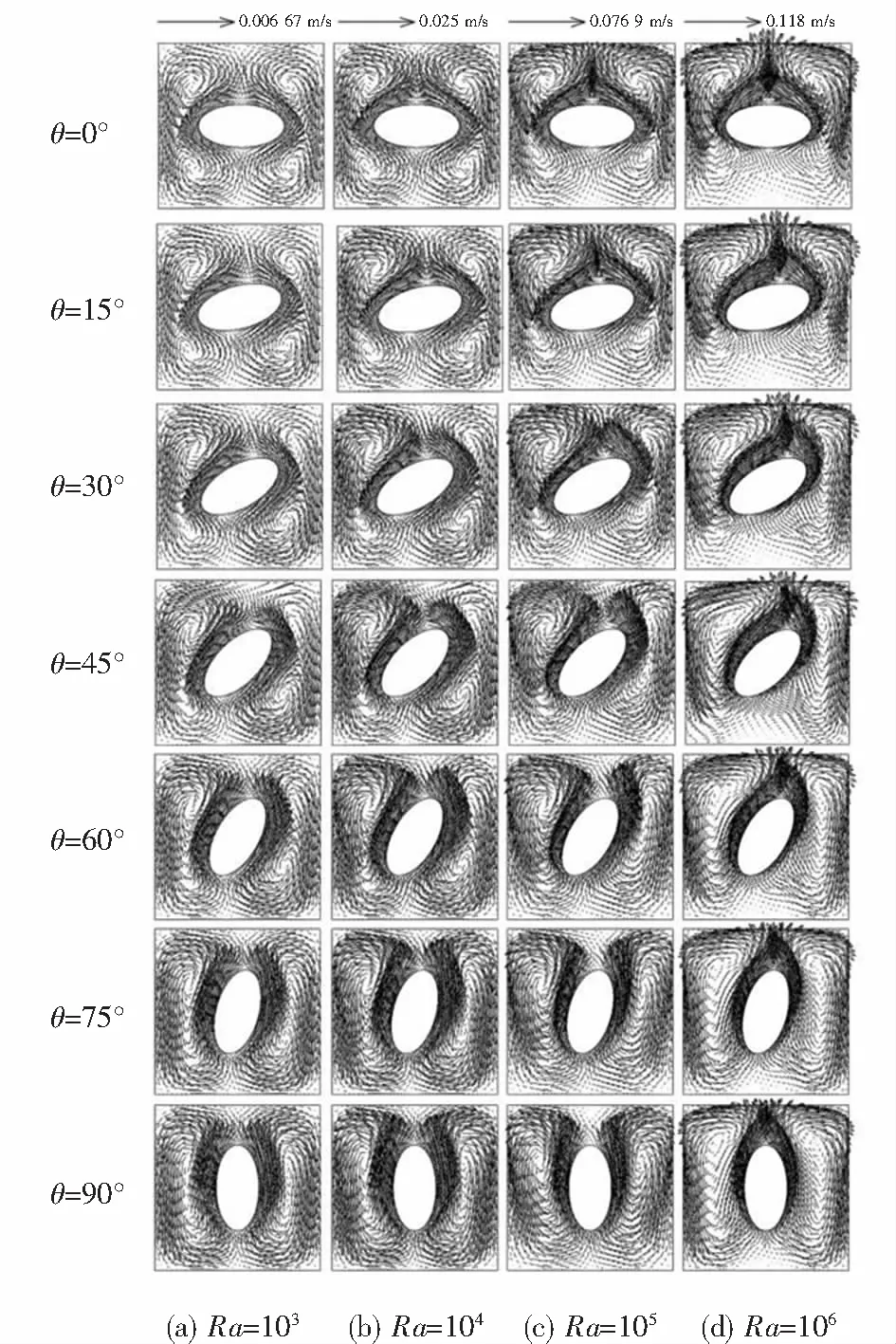
图4 不同Ra、θ时方腔内速度场Fig.4 Velocity field with different Ra and θ

图5为不同Ra、θ时的等温线.Ra较小时，方腔内对流较弱，方腔内等温线分布变化较小，发热体体周围温度梯度相对较大.随着Ra的增加，浮升力增大对流增强，发热体下部和方腔上部温度梯度逐渐增大而发热体上部和方腔下部温度梯度逐渐减小，发热体上方羽流逐渐明显且随着Ra的增大羽流区域逐渐增大.在相同Ra下，发热体到上壁面间区域随着θ的增加逐渐减小，羽流区域也逐渐减小，侧壁面与发热体之间锯齿状的等温线更加明显.

图5 不同θ、Ra时方腔内温度场Fig.5 Isotherm with different Ra and θ

2.2 Ra、θ对壁面局部Nulocal的影响

不同Ra和倾角θ下，椭圆发热体表面Nulocal的分布如图6所示.随着Ra的增大，Nulocal逐渐增大.在θ=0°和90°时，椭圆发热体表面Nulocal关于φ=90°和270°对称分布.不同Ra下，椭圆发热体表面Nulocal的分布规律相差较大.Ra=103时，方腔内对流较弱，内置椭圆发热体Nulocal在长短轴间表面上的分布差别很小，Nulocal基本关于极值点对称分布；在长轴端点处具有极大值，而在短轴端点处取得极小值；随着倾角θ在0～90°间变化，极大值先减小后增大，在θ=45°时极大值最小；椭圆发热体倾角对发热体表面换热的影响很小，不同倾角下发热体表面Nulocal差别不大.随着Ra增大，方腔内对流增强，椭圆发热体表面各部分间Nulocal的差别逐渐增大，倾角对发热体表面Nulocal的影响也逐渐增大；发热体下部极大值逐渐增大，而上部极大值逐渐减小；在发热体上部出现羽流后，上部极大值逐渐变为极小值，且极小值随着发热体上部羽流区的增大而逐渐减小.

图6 内热源表面Nulocal分布Fig.6 Nulocal along the surface of the inner cylinder

不同Ra下，方腔四周壁面Nulocal随椭圆发热体倾角θ的变化如图7所示.壁面Nulocal极小值出现在方腔顶角处；极大值在Ra≤104时基本出现在壁面中间位置；而在Ra>104时，壁面极大值受椭圆发热体倾角的影响显著.随着Ra的增加，上壁面及侧壁面Nulocal逐渐增大，而下壁面Nulocal逐渐增小；上壁面Nulocal显著增加，而侧壁面Nulocal增加相对较小，不同壁面间的差别逐渐增大；侧壁面极大值的位置由侧壁面中点逐渐向靠近上壁面处移动.上下壁面Nulocal基本随着倾角的增大而增大，而左右壁面Nulocal随着倾角的增大而减小.

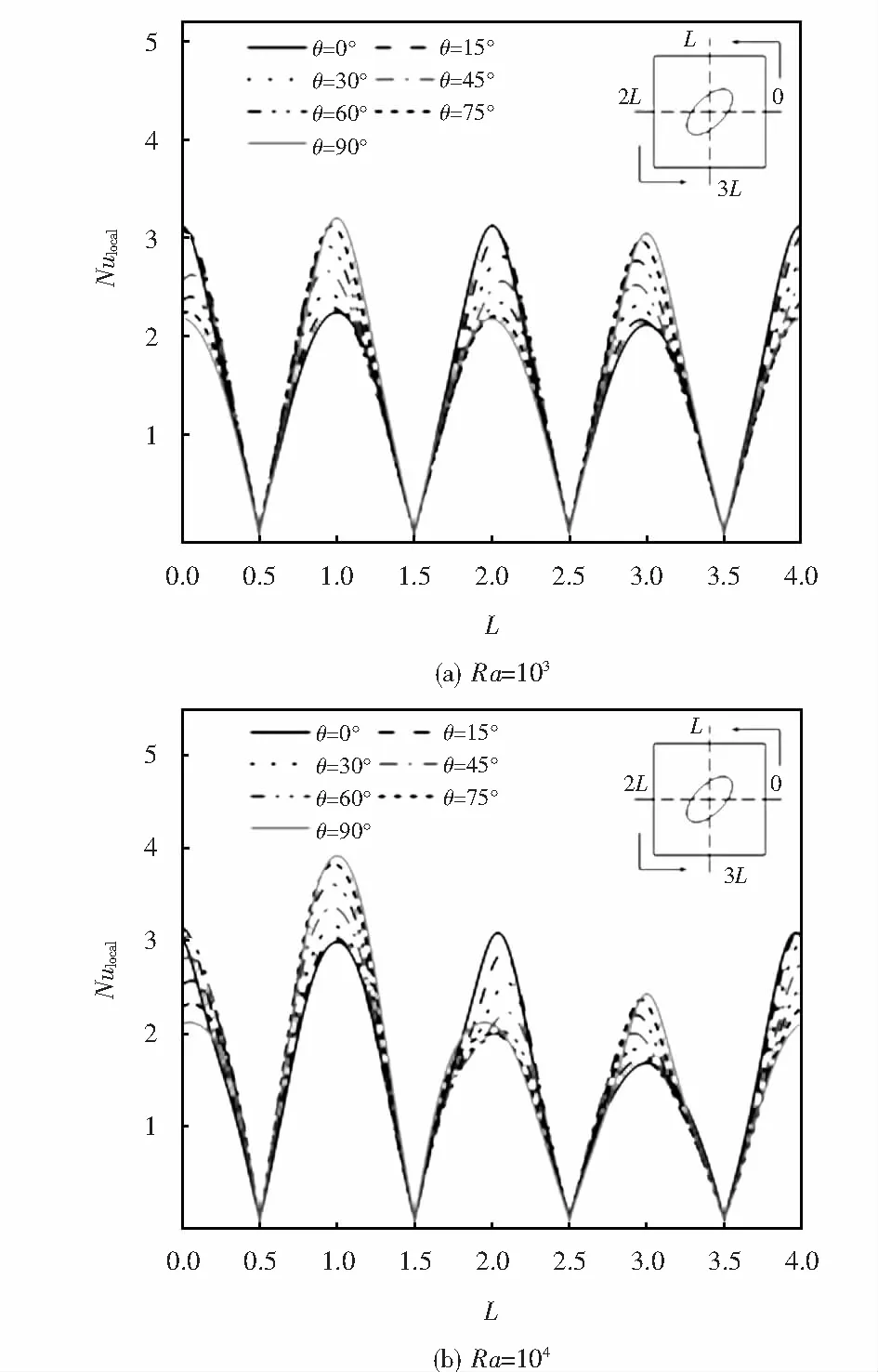
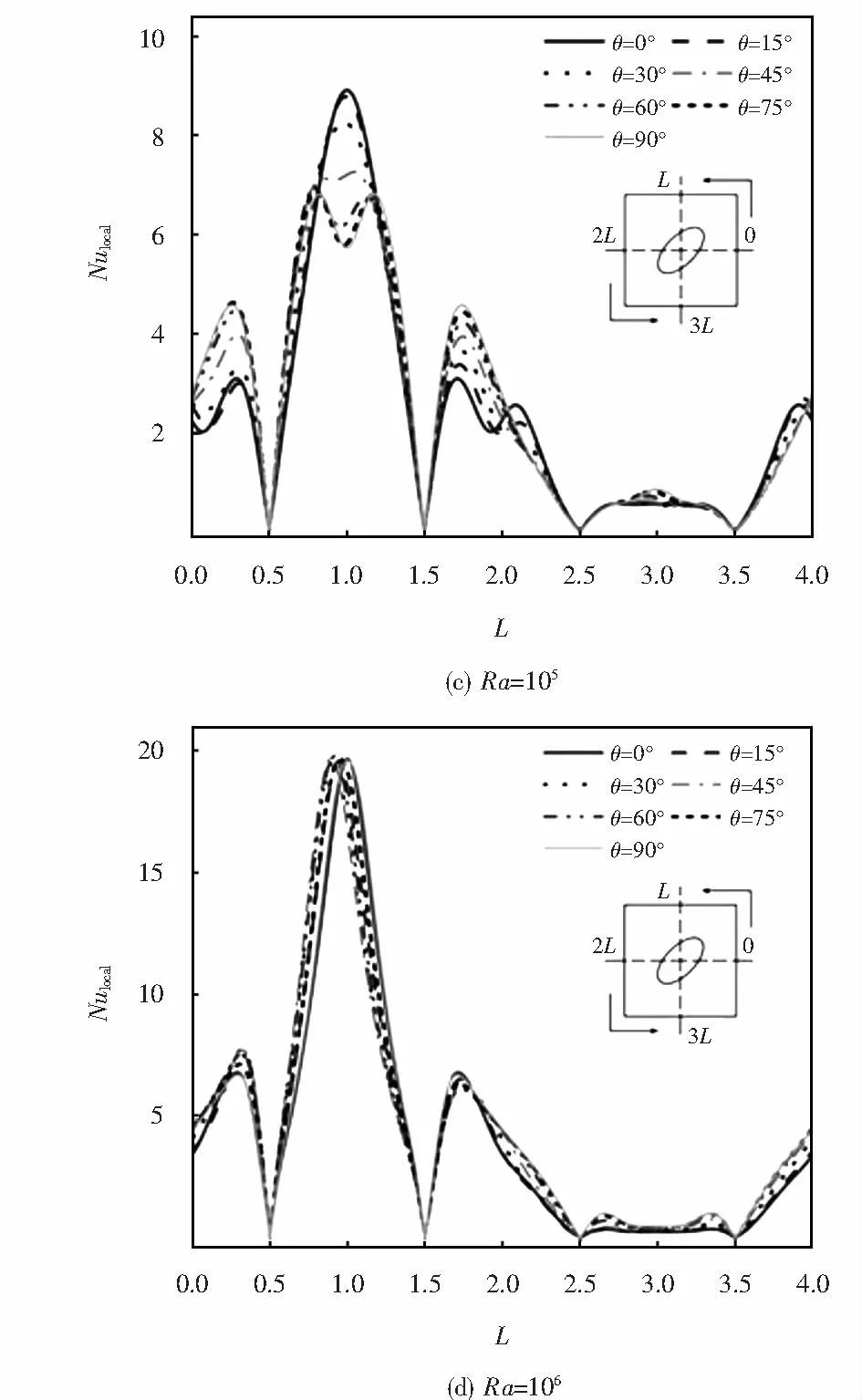
图7 方腔壁面Nulocal分布Fig.7 Nulocal along the walls of the enclosure

2.3 Ra，θ对壁面平均Nu的影响

方腔上、下壁面平均NuT、NuB随倾角θ的变化如图8所示.随着Ra的增加，浮升力增大方腔内对流增强，不同倾角下NuT逐渐增大；θ小于45°时，NuB随Ra的增大逐渐减小，在θ>45°时，NuB随Ra的增大先减小后增大；Ra=106时，由于方腔内左右两侧涡合并使得下壁面附近速度增大，下壁面附近对流要强于Ra=105时的对流，因此，Ra=106时NuB略大于Ra=105时的值.Ra=103、104、106时，NuT和NuB随着θ的增加而增加.而Ra=105时，NuT在θ=0°～30°时的差别很小；当θ=45°～90°时，随着θ的增加，羽流区域减小使得上壁面NuT减小；随着θ的增大，受方腔两侧涡的影响，下壁面附近速度增大，NuB逐渐增大.

图8 θ对方腔上、下壁面Nu的影响Fig.8 Effect of θ on NuT and NuB

方腔侧壁面的平均NuL、NuR随θ的变化如图9所示.不同Ra数下，θ=0°、90°时流场对称，NuL与NuR相等.Ra≤104时，NuL、NuR基本随着θ的增加逐渐减小；Ra=105时，NuL、NuR随着θ的增大逐渐增加；Ra=106时，NuL随着θ的增大先减小后增大，θ=15°时的NuL最小；NuR随着θ的增加先增加后减小，θ=60°时NuR最大.

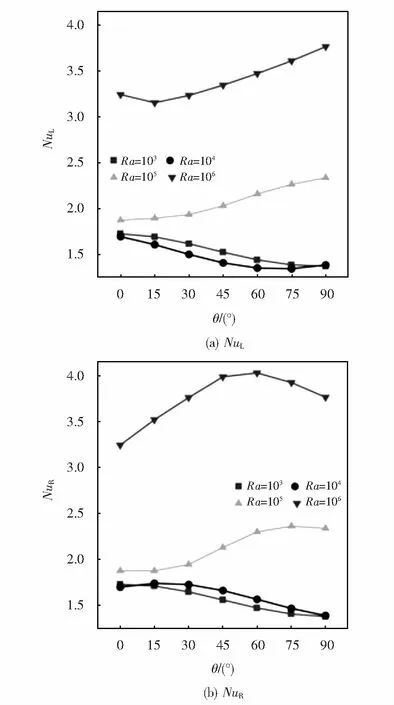
图9 θ对方腔左、右壁面Nu的影响Fig.9 Effect of θ on NuL and NuR

图10为不同Ra时，发热体表面和方腔壁面的平均NuC、NuEN随倾角θ的变化关系.NuC、NuEN与随Ra的增大而增大.Ra=103～104时，θ对NuC、NuEN的影响较小，Ra=103时，不同θ下的NuC、NuEN关于θ=45°对称分布，且θ=45°时的NuC、NuEN最小.此时椭圆形发热体的NuC、NuEN均小于圆形发热体的NuC、NuEN.Ra≥105时，NuC、NuEN随着θ的增加而增大；θ=45°时椭圆形发热体与圆形发热体NuC差别不大.θ<45°时，椭圆形发热体的NuC、NuEN小于对应圆形发热体的值.而θ>45°时，椭圆形发热体的NuC、NuEN大于对应圆形发热体的值.Ra=106、θ=90°时椭圆形发热体的NuC、NuEN相对θ=0°时提高10.8%.

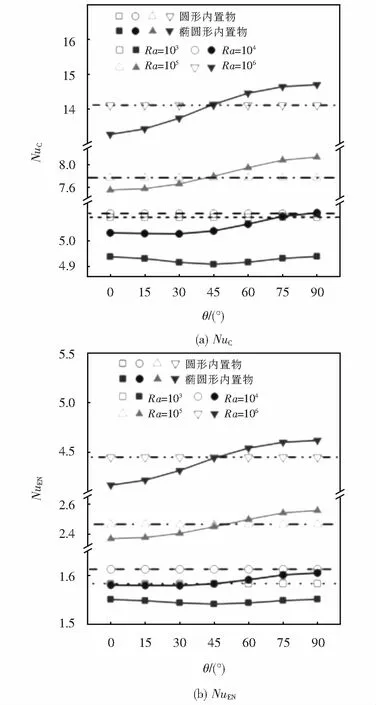
图10 θ对NuC和NuEN的影响Fig.10 Effect of θ on NuC and NuEN

3 结论

本文在Ra=103～106范围内，分析了椭圆内置发热体倾角对方腔内自然对流的影响，主要结论如下：

1)Ra较小时，椭圆形发热体倾角对方腔内自然对流换热的影响较小；随着Ra数增大，方腔内Nu随着倾角的增大而显著增大.

2) 羽流的产生降低了发热体局部换热，随着倾角的增大，羽流区减小，发热体对应区域的局部换热增强.

3)θ=90°时椭圆形发热体的换热最强，与θ=0°时相比，椭圆形内置发热体表面Nu在Ra=106时提高10.8%.

4) 当Ra=103～104及Ra=105～106且θ<45°时，椭圆形发热体Nu均小于圆形发热体；当Ra=105～106且θ>45°时，椭圆形发热体Nu相对等周长圆形发热体在θ=90°时最大提高4.6%.