基于kNN发现社团主干的社团检测算法
2021-07-16李明,陈梅,张梅
李 明,陈 梅,张 梅
(兰州交通大学 电子与信息工程学院,兰州 730070)
社团检测可以发现复杂网络中结构或功能相似的模块[1],对复杂网络进行社团检测可以揭示网络隐含的结构和潜在的功能,有极为重要的现实意义[2].研究人员提出了大量的社团检测算法,主要有基于模块度[3]、基于标签传播[4]、基于随机游走[5]和基于相邻节点关系[6]的社团检测算法.基于模块度的方法有追求模块度最大化的Fast Q[3]算法;基于标签传播的方法有根据节点邻居更新节点标签的LPA(label propagation algorithm,LPA)[4]算法;基于随机游走的约束游走过程的Synwalk[5]算法;基于节点间关系的社团检测算法有Black Hole[7]算法、DA(a divide and agglomerate algorithm,DA)[8]算法和棒不打鸳鸯[6]算法.
由于基于节点间关系的社团检测算法可以从网络的拓扑结构层面发现社团结构[8],近年来,研究人员提出了大量该类的社团检测算法.基于节点间引力与斥力的Black Hole算法通过得到使得整个网络合力最小的分布来检测社团结构;基于全局局部关系的DA算法侧重于同时从全局和局部角度考虑检测社团结构,并在分配无类标节点时利用节点间的影响力对其进行分配[9];棒不打鸳鸯算法则从“两个互近邻节点极有可能属于同一个社团”出发生成树状图并剪枝检测社团结构.然而,当需要检测任意结构任意规模的网络时,这些算法就难以检测到准确的社团结构了.
为了检测任意结构任意规模的社团,本文提出了一种简单、高效和时间复杂度低的基于k最近邻发现社团主干的社团检测算法DCCB.DCCB算法的核心在于:它根据相似节点对及其kNN(knearest neighbors,kNN)邻居生成的社团主干进行聚类,并利用互kNN连接的关系对社团主干进行扩展,克服了棒不打鸳鸯算法仅从一个社团核心出发的局限性.此外,DCCB利用kNN扩展社团主干,这种方法认为社团内所有节点都以互kNN方式相连,这使得DCCB算法能不受社团结构和规模限制,检测出正确的社团主干;得到社团主干后,检测异常节点,并将其标记为无类标节点;分配无类标节点时,借鉴DA算法的无类标节点分配模式,使用节点间影响力分配无类标节点即可得到最终的社团结构.
1 相关定义
1.1 网络的定义
网络G可表示为G=(V,E).其中V表示节点集,E表示边集.记|V|为n,表示网络节点数.记|E|为m,表示网络边数.若G中∀xi,xj∈V,∃(xi,xj)⊆E,∃(xj,xi)⊆E且满足(xi,xj)=(xj,xi),则该网络中的边没有方向,那么称图G为无向网络(undirected network).对于网络G,若∃(xi,xj)⊆E,则节点xi与节点xj为邻居节点.通常,对于网络中的一个节点xi,定义它的邻居集合为N(xi),将节点xi邻居的个数|N(xi)|称为节点的度,记作dxi.
1.2 相邻节点之间的相似度
本文采用Jaccard相似度[10]计算两个节点xi与xj的相似度,如公式(1)所示,公式(1)中|coc(xi,xj)|表示节点xi,xj之间公共邻居的个数.
(1)
1.3 k最近邻
x1,x2,…,xi,…,xn是节点集V中的n个节点.对G中的每个节点xi∈V,与xi最相似的k个邻居被称为xi的k最近邻,表示为Nk(xi),Nk(xi)⊆V.
1.4 互k最近邻
给定节点集V中的两个点xi与xj,当且仅当xi∈Nk(xj)且xj∈Nk(xi)时,称xi与xj为互k最近邻 (mutualknearest neighbors,MkNN).如果xi和xj没有出现在另一个点的k最近邻中,xi与xj就不是互k最近邻,也就是不存在互k最近邻关系.
1.5 共享k最近邻
对于节点xm,如果节点xi和xj为MkNN,且满足xm∈Nk(xi)和xm∈Nk(xj),xm就是xi与xj的共享k最近邻(sharedknearest neighbors,SkNN).
1.6 吸引力
在社团中,存在一些影响力大的核心节点.2019年Li Z团队[9]提出了传播者的概念,将该类节点称为传播者,可通过传播者对其它节点的影响对无标签节点进行合理分配.本文定义节点xi对节点xj的吸引力为gravity(xi,xj),如公式(2)所示,其中Jaccard(xi,xj)可由公式(1)计算.在处理无标签节点时,可以通过计算吸引力对该节点进行合理分配.
gravity(xi,xj)=dxi·Jaccard(xi,xj).
(2)
2 基于kNN发现社团主干的社团检测算法
本节将对DCCB算法进行详细叙述.首先叙述提出该算法的动机并给出算法整体流程图;然后详细叙述该算法的核心部分,即基于kNN合并社团主干;接着描述无标签节点的分配;最后对该算法的时间复杂度进行分析.
2.1 动机
通过认真研究网络的社团结构,可以发现网络中互为近邻且相似度很高的一对节点极有可能在一个社团中.这里以图1中所示的空手道社交网络[11]进行举例说明,该网络右侧社团中的“1”号节点和“2”号节点互为近邻且相似度较高.这对节点就是核心节点,该社团中的其余节点都与核心节点存在互近邻关系.这些核心节点与人际关系中的领袖类似,即一个团体中其余的人或多或少受领袖的影响,这对核心节点与核心节点的邻居组成的小社团就是社团主干.受此启发,提出了基于相似近邻节点发现社团主干的算法DCCB;该算法首先利用互k最近邻找到相似度较高的一对节点,接着将这对节点及他们的共享k最近邻作为社团主干,这样可以最大可能地找到与他们相似的节点,即这两个人的共同朋友;最后通过互近邻扩展社团主干,利用网络中节点的相似性以及近邻关系进行社团检测.

图1 空手道社交网络Fig.1 Karate Network
2.2 算法流程图
本节将对算法的具体流程进行阐述.图2(a)为DCCB算法的整体流程图,图2(b)为基于kNN合并社团主干的具体流程.
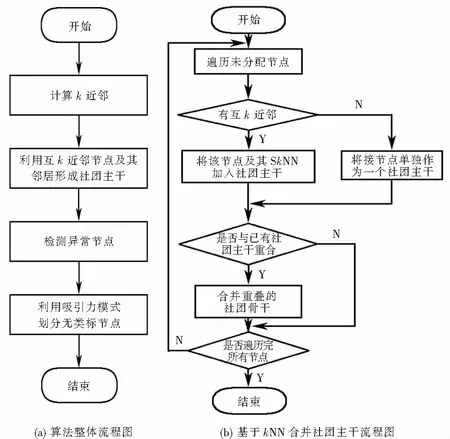
图2 算法流程图Fig.2 Algorithm flow chart
2.3 基于kNN合并社团主干
在识别社团主干时,DCCB算法只需一个输入参数k,即最近邻个数.开始寻找社团主干时,该算法首先从一个从未访问过的节点xi开始遍历,若xi存在互k最近邻xj,则将xi、xj以及它们的共享k最近邻节点集合在一起去生成初始的社团主干.若xi不存在互k最近邻,则将xi单独当作一个社团主干,在检测异常节点时再处理.这种互kNN的连接方法使得DCCB能够发现任意互k最近邻节点所组成的社团.该种方法生成的社团主干受社团结构规模影响较小,可以尽可能的将相似的节点及与它们联系紧密的邻居节点划分到同一个社团中去.社团主干所属的社团一般由一个或多个社团主干构成,若两个社团主干之间存在重叠的节点,则说明这两个社团主干属于同一个社团,应当合并.找到所有社团主干后,用吸引力可轻易的将社团中其余节点划分到与它有邻居关系的社团主干中去,得到最终的社团结构.
为了更直观明了的展示该过程,将对该过程进行可视化描述,具体步骤如图3所示.图3(a)表示初始网络,该网络由3个小网络构成.图3(b)中,从节点“0”出发,找到该节点的互k最近邻节点“1”,然后发现该节点对的共享k最近邻节点“3”,就找到了该社团的主干.图3(c)中,从节点“1”出发,找到该节点的互k最近邻节点“3”,然后发现该节点对的共享k最近邻节点“2”.此时,由于节点“1”和节点“3”在已有社团主干中,将节点“2”加入到该社团主干中.图3(d)中,继续通过社团主干的合并将节点“4”纳入进去,即得到第一个社团的社团主干.图3(e)中,由于节点“5”没有互k最近邻节点,将该节点搁置.图3(f)与图3(g)中,则采用与找第一个社团主干同样的方法找第二个社团主干.最终,通过kNN合并社团主干,得到了正确的社团主干,如图3(h)所示.
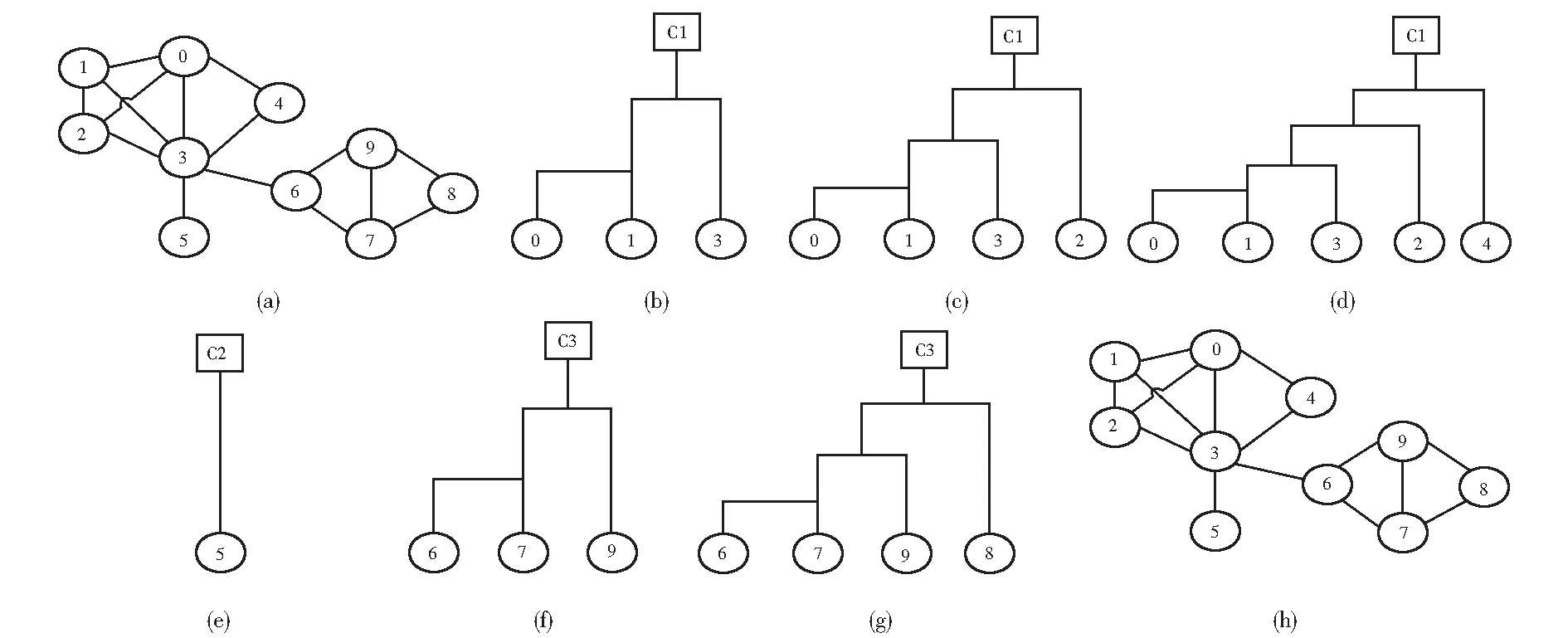
图3 社团主干的生成Fig.3 Generation of the community backbone
2.4 异常点检测及无标签节点的分配
DCCB算法识别社团主干时,会将不存在互k最近邻的单个节点,包含2个节点及1个共同邻居的3个节点作为社团主干加入到已有社团主干中.生成社团主干时若该类节点无法吸引外部节点,则说明该类节点不是社团主干,需要重新划分.DCCB算法检测异常节点时,将包含节点数小于3的社团主干中的节点分配到无类标节点中重新划分.
DCCB算法在进行无类标节点的分配时,借鉴了LPA算法以及LGM&GM[9]模式.该模式认为节点的影响力与节点度的大小成正比,度越大影响力越大,综合考量节点的度以及两个节点间的相似性,提出了节点间的吸引力.在分配时,首先利用公式(2)找到对无类标节点吸引力最大的邻居节点,然后将该无类标节点划分到邻居节点所在社团主干,得到最终的社团结构.
2.5 时间复杂度分析
DCCB算法计算k近邻时,用“k-d tree”实现,时间复杂度为O(n·logn),其中n为节点集V中节点的个数.计算k近邻与形成社团主干时间复杂度为O(n·k),其中n为图中节点的个数,k为每个点最近邻个数,由于k≪n,这2个步骤时间复杂度可近似的认为是O(n).
检测异常节点时查找包含节点小于等于3的社团主干时间复杂度为O(n).划分无类标节点的时间复杂度为O(z·davg),z表示无类标节点数,davg表示节点的平均度.由于davg≪z,分配无类标节点的时间复杂度为O(z).整个算法时间复杂度为O(n·logn+n+n+z),由于O(z)和O(n)时间复杂度相当,且n≪n·logn,所以DCCB的时间复杂度为O(n·logn).
3 实验结果与分析
为了检验DCCB算法能否检测出不同结构不同规模的社团,本节实验选取了4个便于可视化展示的不同结构的真实网络以及3个不同规模的人工合成网络[12],并与常见的5个社团检测算法进行了对比,验证了DCCB算法的有效性及正确性.
3.1 数据集及对比算法
本节的实验使用了表1所示的4个真实网络数据集和3个人工合成网络数据集.4个真实网络数据集是空手道俱乐部网络(Karate)、游戏地图网络(Risk map)、海豚社交网络(Dolphins)和大学生足球联赛赛程表网络(Football)[11].这些网络都是公开发布的真实数据集,网络规模较小,结构各异,便于可视化处理,能直观的展示实验结果.此外,这些网络的真实结构都已知,便于进行指标量化处理,评估不同算法的检测结果.3个不同规模的人工合成网络数据集由LFR(a lancichinetti,s fortunato,f network,LFR)测试网络生成工具程序生成[12],分别包含2 000,5 000和20 000个节点.这些网络的统计信息如表1所列.
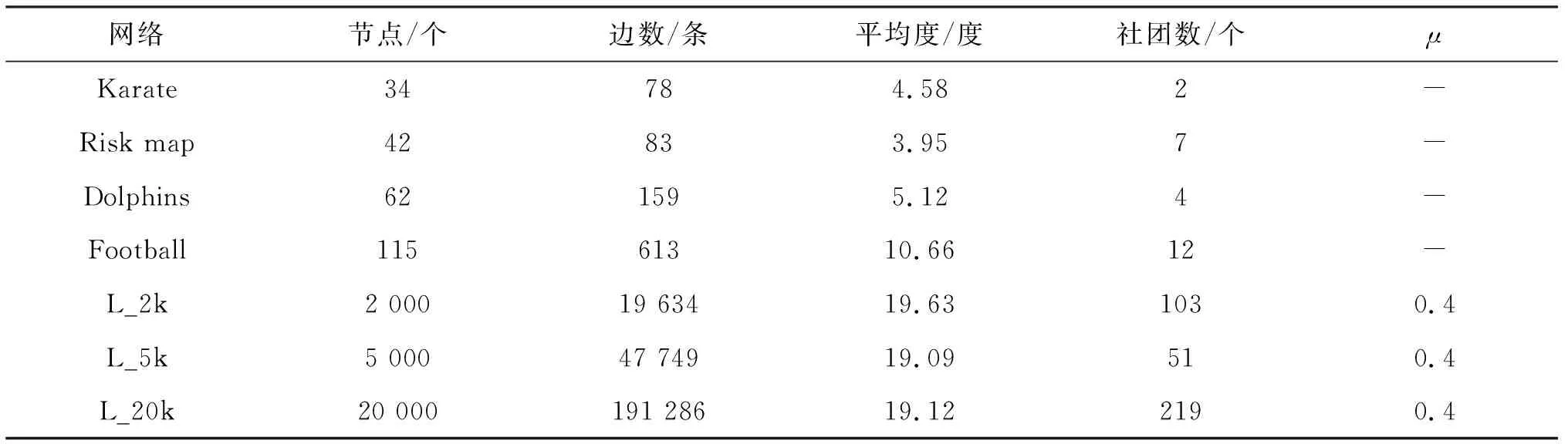
表1 实验所用数据集Tab.1 Networks used in the experiment
LFR人工合成网络需指定参数.为了测试DCCB算法在不同规模社团上的效果,生成了L_2k与L_5k数据集;为了测试DCCB算法在大规模网络上的表现,生成了L_20k数据集;这些数据集参数设置如表2所列.在这些参数中,混合系数μ很关键,若μ>0.5,则生成的社团结构趋于模糊,检测困难;若μ<0.5,则生成的社团结构很清晰,易于检测.由于实验需要验证DCCB算法在不同规模网络上的效果,这3个网络混合系数μ设置为0.4即可.
本文选取5个典型的社团检测算法作为对比算法,包括模块度最优算法(Fast Q,FQ)[3]、典型的标签传播算法LPA[4]算法、经典的谱聚类算法(Spectral Clustering,SC)[13]、新型的基于节点间作用的算法(Attractor,Att)[14]以及基于吸引力模式的算法(Black Hole,BH)[7].为了更直观的看出算法在数据集上的表现,本文采用了2个常用的评价指标,即归一化互信息量(normalized mutual information,NMI)和调整兰德指数(adjusted Rand index,ARI)来对不同算法做统一衡量.对于不稳定的算法,评价指标取运行30次该算法结果的平均值,结果图为检测到的社团结构评价指标最高的一次.
3.2 真实网络的结果分析
3.2.1 Karate网络的结果分析
图4展示了DCCB与5种对比算法在Karate数据集上的社团检测结果.从图4中可以看出,Fast Q算法,Spectral Clustering算法以及Black Hole算法检测效果不佳,未能得到清晰良好的社团划分.DCCB算法、Attractor算法表现良好,能得到质量较高的社团结构.DCCB算法除了将节点32划分错误外,其余节点都被正确地划分到了相应的社团.图4(c)是LPA在Karate上最好的检测结果,该次结果错误地划分了节点3,但从表3可以看到该算法多次得到的结果评价指标平均值较DCCB算法差.Fast Q算法和Black Hole算法表现较差,SC算法错误地划分了节点3、节点20和节点14.Attractor算法除了将节点10划分错误外,其余的节点都划分正确.Black Hole算法将网络划分为4个社团.
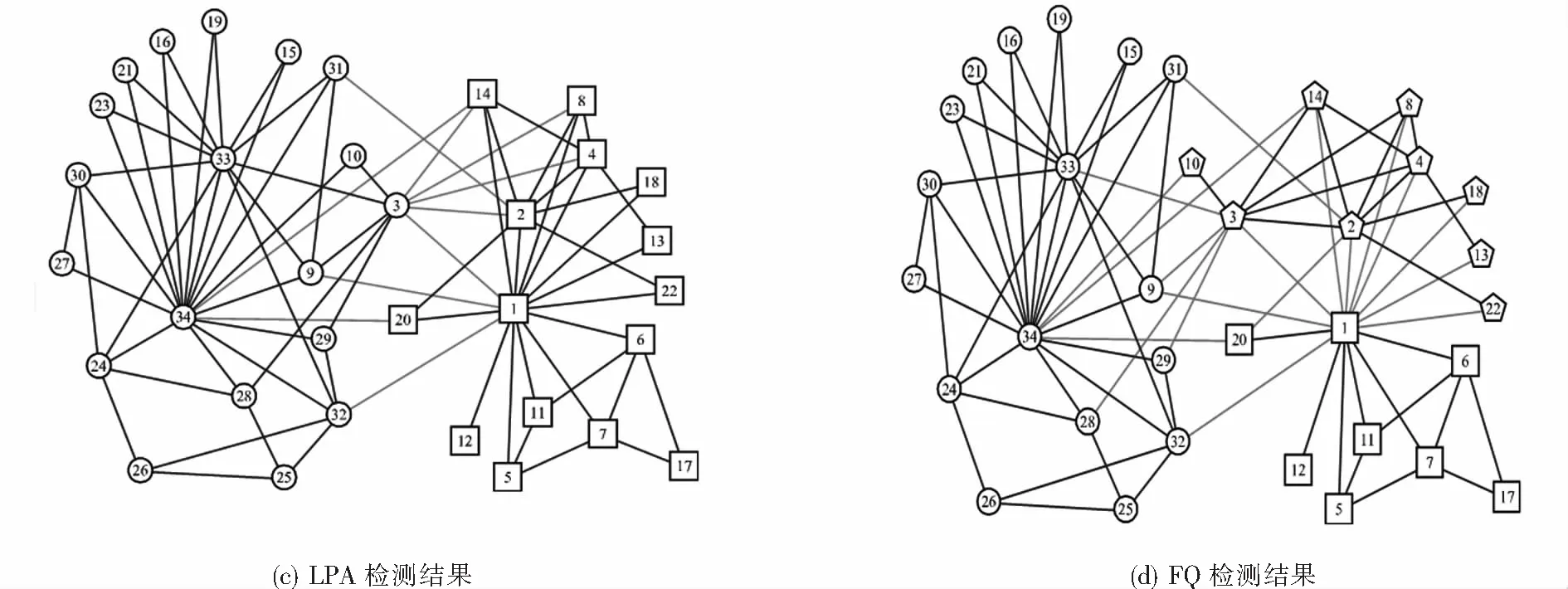
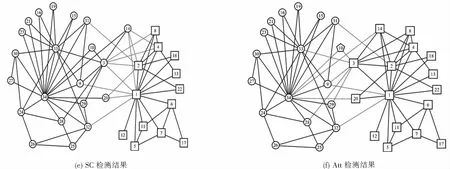
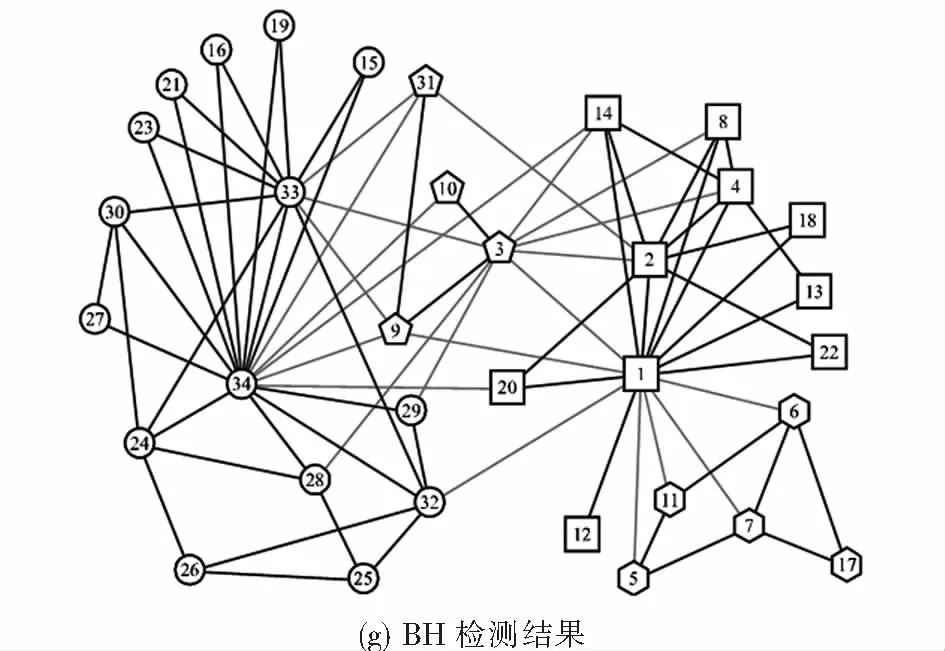
图4 Karate网络上的检测结果Fig.4 Detection results on Karate network
3.2.2 Risk map网络的结果分析
图5展示了DCCB与5种对比算法在Risk map数据集上的聚类结果.可以从图5(b)明显看到:DCCB算法除了将节点26划分错误外,其余节点都被正确地划分到了相应的社团,且成功检测了右上角较难检测的2个社团.从表3也可以看到,DCCB得到了最高的ARI和NMI值,较其它5个对比算法划分的社团结构更准确.从图5可看出,算法LPA、Fast Q和Spectral Clustering分配的结果都不太理想,未能成功地检测出良好的社团结构.网络右侧的两个社团比较难检测,基于互近邻的DCCB在该网络表现良好,可以检测出该社团.
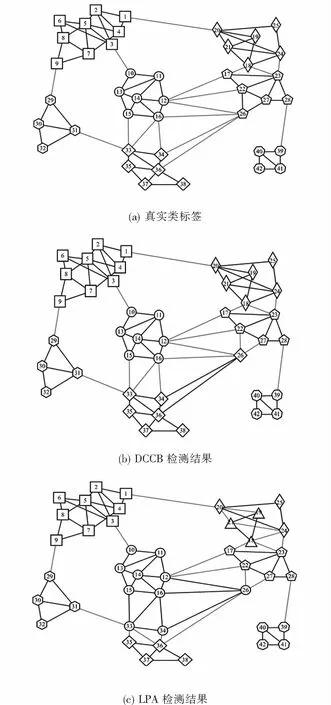
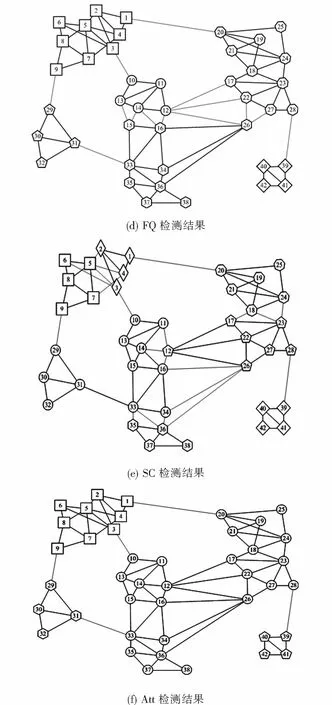
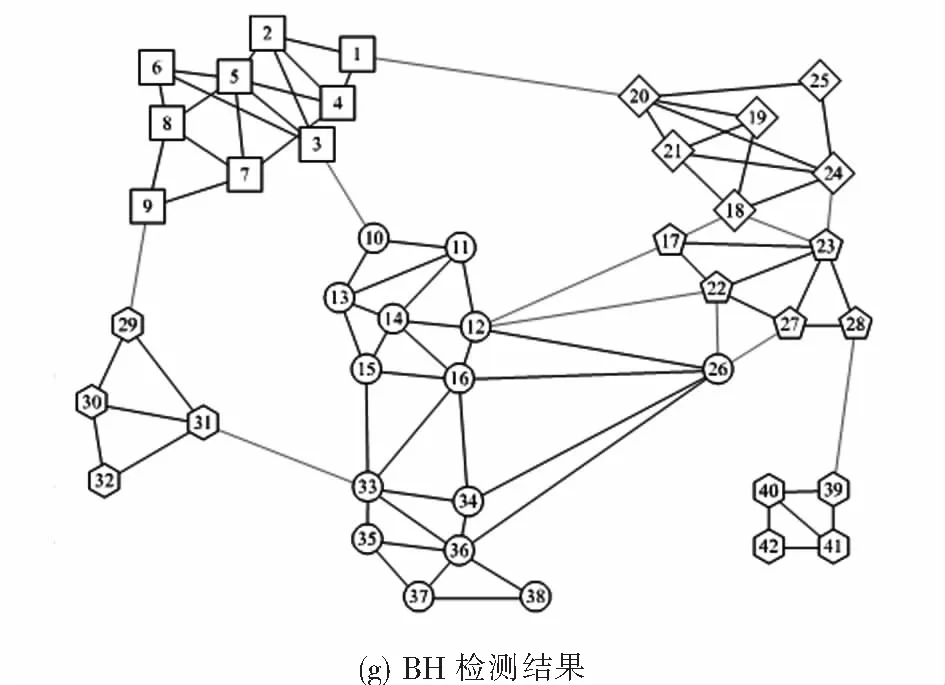
图5 Risk map网络上的检测结果Fig.5 Detection results on Risk map network
3.2.3 Dolphins网络的结果分析
图6展示了DCCB与5种对比算法在Dolphins数据集上的聚类结果.图6(a)是Dolphins的真实社团结构,图6(b)为DCCB算法的社团检测结果.该网络结构比较复杂,难以检测.从图6与表3可以看出,大部分算法在该网络上表现不太好,但DCCB仍然能检测出高质量的社团结构,且比其它5个对比算法检测出的结果更优.通过图6(c)可以看出,LPA算法、Fast Q算法、Spectral Clustering、Attractor以及Black Hole算法在Dolphins数据集上的实验结果并不理想,得到的社团结构与真实的社团结构有很大偏差.从表3可以看到,DCCB得到了最高的ARI和NMI值,较其它5个对比算法划分的社团结构更准确.从图6(b)可以看到,DCCB算法除了将社团边缘的3个节点8、40及60分配错误外,其余节点均分配正确.
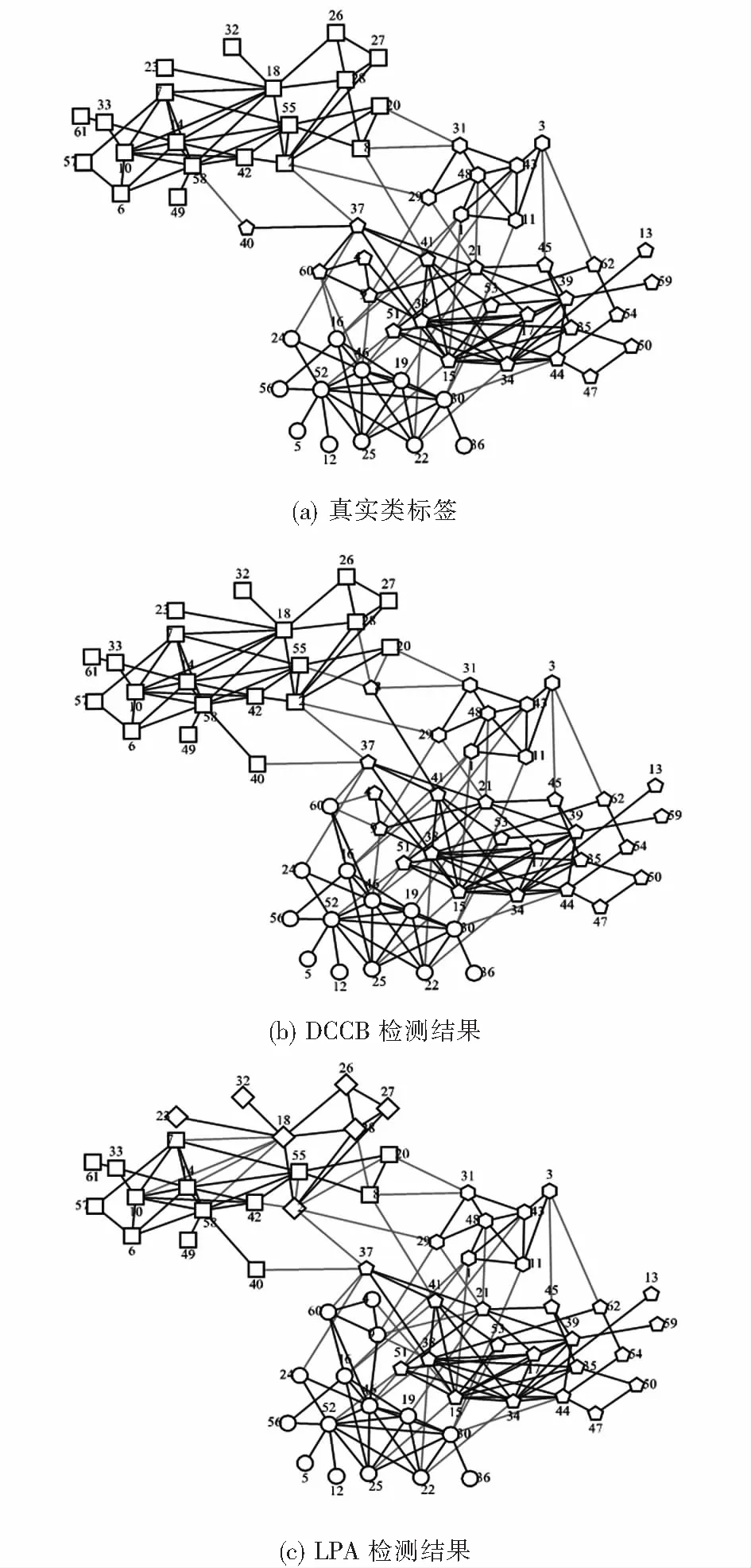
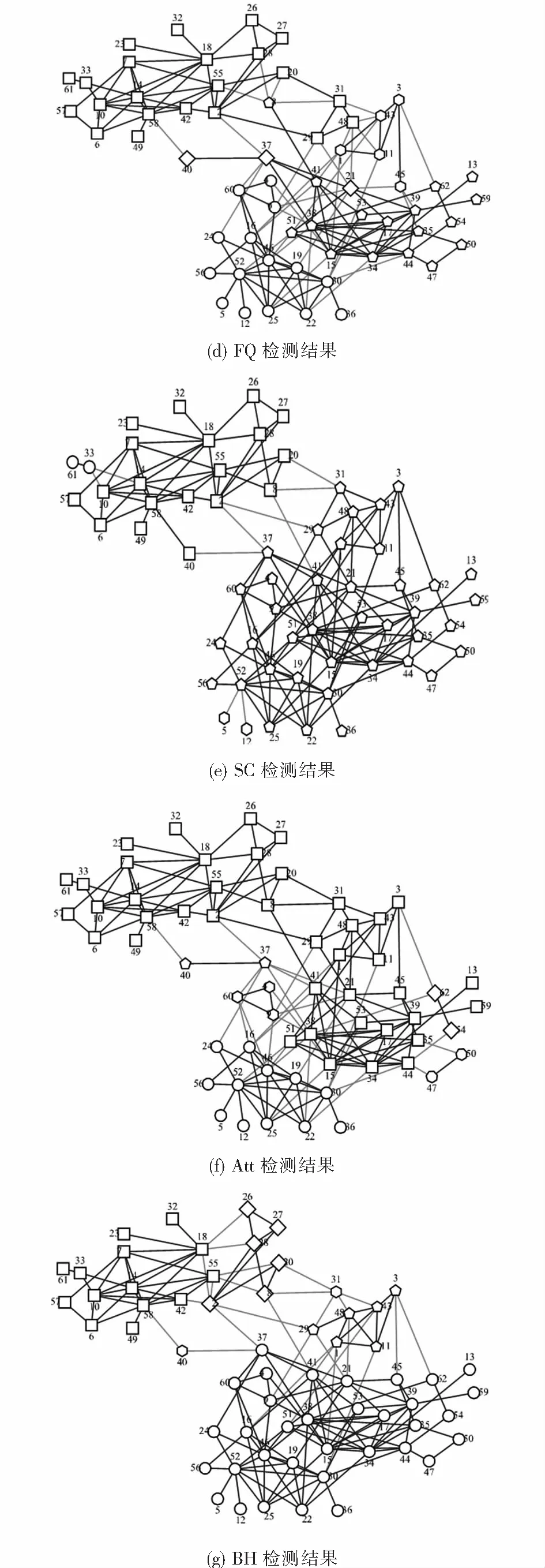
图6 Dolphins网络上的检测结果Fig.6 Detection results on Dolphins network
3.2.4 Football网络的结果分析
图7展示了DCCB与5种对比算法在Football数据集上的聚类结果.图7(a)是Football的真实社团结构,图7(b)为DCCB算法的社团检测结果.DCCB除了将中间的一个包含4个节点的小社团错误划分到左上角社团外,其余部分的社团结构完全正确.Attractor算法划分时也错误地将左上角社团的一个节点划分给该小社团.从表3可以看出,Attractor算法、DCCB算法以及Black Hole算法在该网络表现良好,其余几个算法在该网络表现较差.
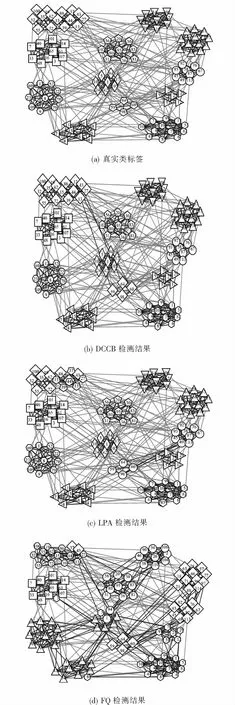

图7 Football网络上的检测结果Fig.7 Detection results on Football network
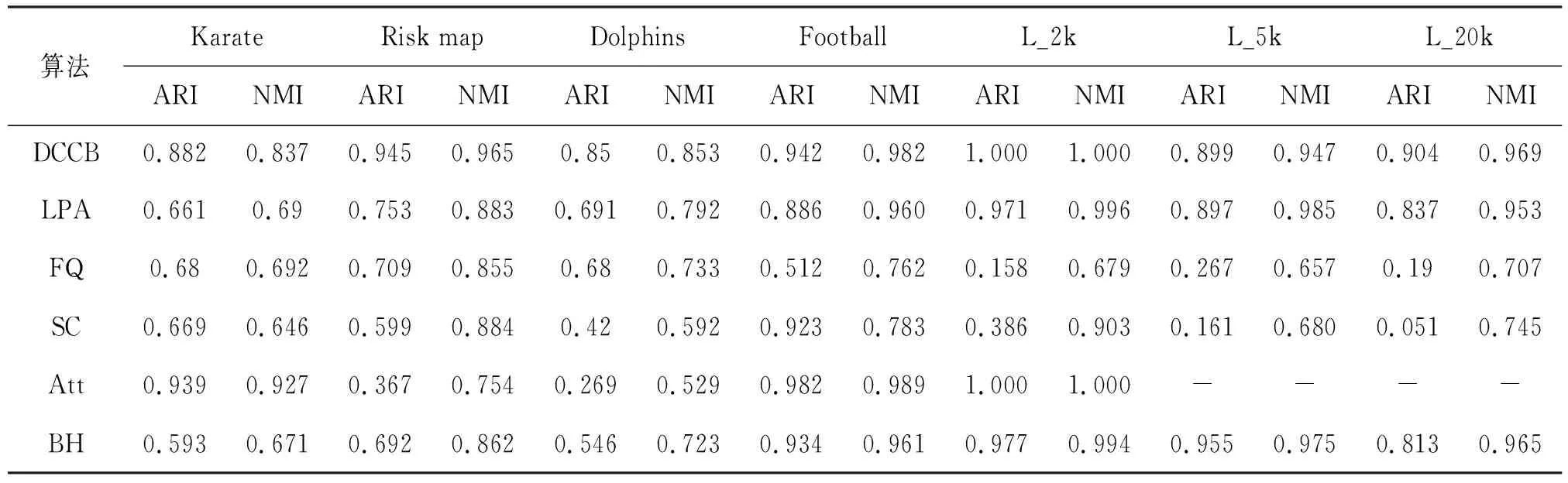
表3 多个有真实标签网络数据集检测结果比较Tab.3 A comparison of detection results on the various network datasets with ground truth
3.3 LFR网络的结果分析
L_2k数据集有2 000个节点,包含103个社团.从表3可以看出,在该网络上,DCCB方法得到的ARI及NMI均为最大,识别出了完全正确的社团结构.Attractor算法的结果与其相同,Black Hole算法、LPA算法的结果与其比较相近但稍差于DCCB算法,Fast Q算法及Spectral Clustering算法的ARI和NMI均低于DCCB算法.其中,Attractor算法在运行L_5k和L_20k时出现内存错误,未能得到结果.L_5k数据集有5 000个节点,包含219个社团,从表3可以看出,在该网络上,DCCB检测到的社团结构的ARI是最高的,其它的社团检测算法除了LPA和Black Hole外社团检测结果并不理想.Black Hole算法在不同数据集上均有良好的表现,在L_5k数据集的结果比DCCB更好.L_20k参数设置与L_5k保持一致,该网络有20 000个节点,包含219个社团,从表3可以看出,DCCB在该网络上的ARI和NMI均为最高,较其它算法表现好.LFR网络上的实验结果表明DCCB能很好的检测出不同规模的社团.
3.4 算法的时间复杂度比较
优秀的算法应有较低的时间复杂度[15-17].Spectral Clustering时间复杂度O(n3);Fast Q的时间复杂度为O(n2);LPA的时间复杂度为O(n),但该算法结果不稳定且准确度很差.Attractor算法时间复杂度为O(m+am+Tm),其中:a为两节点间外部邻居的平均数;T为迭代次数.Black Hole算法的时间复杂度为O(n·logn).DCCB的时间复杂度为O(n·logn).总体来说,DCCB时间复杂度较低,且能得到较准确的社团结构.
3.5 总体分析
为量化分析DCCB算法以及其它5个算法的效果,选取了两个社团检测中最常见的评价指标ARI、NMI对社团检测结果量化分析,结果如表3所示.除了在Football数据集上较Attractor算法稍差,在L_5k数据集上较Black Hole算法稍差,在其余5个数据集上,DCCB检测到的社团质量较其它算法都好.对不同算法在不同数据集上的量化评价指标ARI、NMI取均值,如图8所示,很明显DCCB算法取得的ARI、NMI均值是最高的,优于其它算法.此外,本节还采用盒图作为可视化统计方法,对算法的表现进行评估,如图9所示.在7个数据集上,对于ARI、NMI这两个评价指标,DCCB算法在四分位数、中位数、最大值及最小值均有着优秀的表现.L_2k以及L_5k人工合成网络的实验表明,DCCB可以准确识别出不同规模的社团.L_20k数据集上的实验表明,DCCB在规模较大数据集上发挥稳定,可以检测到高质量的社团划分.综上所述,DCCB是一个简单、时间复杂度较低、结果稳定且能在不同结构不同规模网络中检测到高质量社团结构的社团检测算法.

图8 DCCB及对比算法在不同数据集上ARI,NMI均值比较Fig.8 A comparison of average ARI,NMI on the various network datasets with DCCB and contrast algorithms
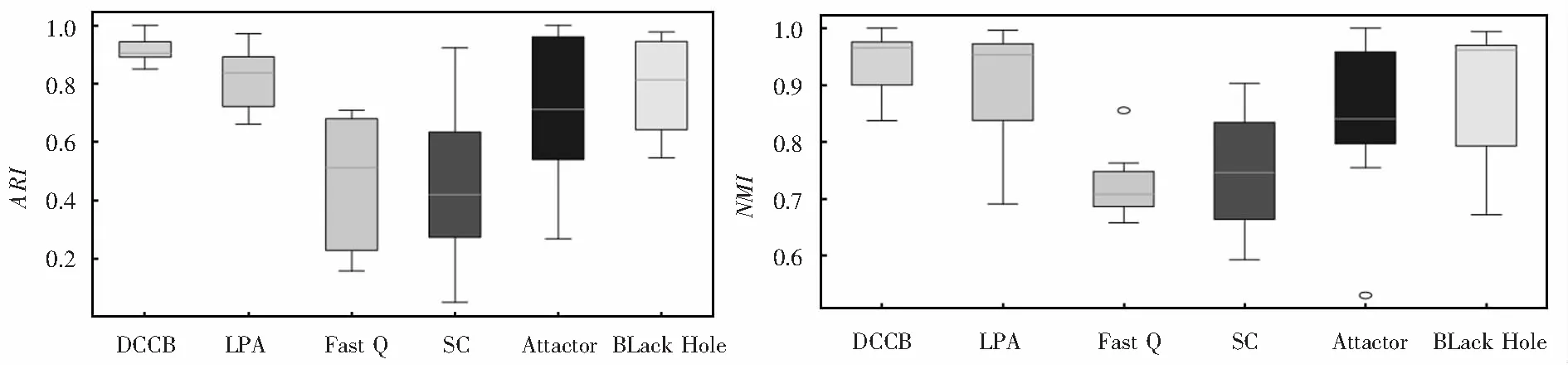
图9 具有真实社团结构网络上的ARI,NMI盒图Fig.9 Box plots of ARI,NMI on the networks with ground-truth community structures
4 结论
本文提出了一种基于kNN发现社团主干的社团检测算法,在4个不同结构真实网络和3个不同规模的人工合成网络进行实验,并与5个常见的社团检测算法对比,得到以下结论:
1) 基于kNN发现社团主干的社团检测方法可有效解决现有的社团检测算法不能很好的检测出任意结构任意规模社团的问题,且该算法时间复杂度较低,提高了社团检测效率.
2) 本文提出了通过互kNN连接发现社团主干的方法,该方法具有良好的应用价值和适用性,对于社团检测及聚类的相关研究,都有良好的借鉴价值.
3) 在实验过程中,发现该算法合并社团主干时容易混淆社团边界处的节点.可通过引入目标函数的方法对社团主干的合并过程进行约束,来得到准确度更高的社团结构.
