地铁隧道纵坡坡型对隧道内压力波的影响分析
2021-07-16万有财姚富宏梅元贵
万有财,姚富宏,梅元贵*
(1. 兰州交通大学 甘肃省轨道交通力学应用工程实验室,兰州 730070;2. 中铁二院工程集团有限责任公司,成都 610031)
近年来,我国城市出现了时速100~160公里快速地铁,如运行时速120公里的深圳地铁11号线、上海地铁9号线和16号线;设计时速140公里成都地铁18号线和160公里北京新机场线.随着运营速度的提升,许多空气动力学问题日渐突出,如隧道压力波问题:运营时速120公里的广州地铁3号线出现了司乘人员耳鸣、耳痛等身体不适[1].与高铁相比,地铁列车的密封性差、行车密度、阻塞比大,且地下线路复杂[2].因此,研究地铁隧道压力波十分必要[3].
针对空气动力学问题,国内外学者主要利用:实车试验、模型试验和数值仿真等技术展开研究[4].在地铁隧道压力波方面:Kim等[5-6]利用三维软件选用标准的湍流模型和1/20缩尺实验两种方法研究了地铁隧道压力随时间变化;张寅河等[7]研究某型地铁列车实际运行时的车内外压力,结果表明列车满足压力舒适性标准.Niu等[8]利用FLUENT软件采用(RNG)双方程湍流模型研究了地铁列车过隧道时,列车加速度、速度和平台间距对压力的影响;汪波等[9]利用三维仿真软件,研究快速地铁列车不同司机室头型在运行中压力分布,对列车头型研发提供了建议;祝岚等[10]利用FLUENT软件,研究了列车在不同运行场景下的压力波及压力变化率,提出了压力舒适度标准下的最大隧道阻塞比;刘冬雪等[11]利用三维软件采用湍流模型研究了高速地铁A型列车以不同运行方式过隧道时车体表面压力和车内压力变化,提出列车气密指数建议值;文献[12-14]分别采用一维数值方法研究地铁列车通过无坡度隧道时的车内外压力,从压力舒适性角度提出了地铁隧道设计建议.上述研究只针对平直隧道,仅从车体载荷和车内压力舒适性角度重点研究了列车表面压力,未对隧道内压力进行研究.梅元贵等[15]考虑隧道坡度采用一维可压缩非定常不等熵流动模型建立了隧道压力计算方法,但未对复杂的隧道坡型展开研究.
基于此,本文采用一维可压缩非定常不等熵流动模型的广义黎曼变量特征线法,在文献[15]的基础上对源代码程序进行了改进,以国内某条快速地铁线路为背景,在车速和阻塞比一定的条件下,研究单列车通过不同坡型和坡度隧道时,隧道内压力波动特性.
1 研究方法
1.1 物理模型
本文考虑了空气重力沿隧道坡面的分量,基于隧道长度远大于隧道水力直径和列车长度远大于列车与隧道所形成环状空间水力直径两个特点,考虑了空气摩擦、传热等不可逆损失后,将三维可压缩非定常流动简化为一维可压缩非定常不等熵流动.
1.2 数学模型
如图1所示,给出空气在带有坡度的隧道内流动示意图,取虚线所围成的微元控制体建立控制方程,坐标系平行于坡面,坐标原点位于隧道入口端,与水平面呈θ夹角.描述一维可压缩非定常不等熵流动流动的控制方程如下:

图1 空气流动控制体Fig.1 Control body of air flow
连续性方程
(1)
动量方程
(2)
能量方程
(3)
式中:u、p、κ、ρ和a分别为隧道内空气流速、压力、比热比、密度和声速;F为空气流道横截面面积;G为空气与壁面的摩擦项;q为空气与壁面的传热项;ξ为空气与列车壁面的摩擦功;θ为坡度;g为重力加速度;t为时间.
1.3 数值方法
(1)~(3)式构成了一阶拟线性偏微分方程组,本文利用广义黎曼变量特征线方法求解,具体过程参见文献[15].初始条件:隧道内空气静止;隧道内初始大气压取隧道入口端大气压值;不考虑隧道高程差引起的压力变化.文献[15]详细介绍了单列车通过简单结构隧道过程的边界条件:隧道端口边界条件、车头车尾驶入隧道瞬间边界条件、隧道内车头车尾端边界条件和车头车尾驶出隧道瞬间边界条件.
1.4 验证
本文选取英国Patchway[16]隧道实车试验数据验证本文带坡度源代码程序的准确性,隧道为单面坡,试验列车上坡运行.如表1所列,给出了隧道和列车具体参数,隧道内无通风竖井、无辅助坑道,隧道截面积和湿周沿隧道纵向有略微变化,数值计算时的隧道截面积和湿周取平均值.如图2所示,距隧道入口端500 m处监控点压力波动曲线,数值仿真得到的压力波动趋势与实车试验结果吻合度良好,最大正、负压值与实车试验的误差分别2.18%和1.33%.

表1 实车试验隧道和列车参数Tab.1 Structural parameters of full scale testing

图2 程序计算结果与实车试验结果对比Fig.2 Pressure comparison between program calculation results and full scale testing results
2 计算模型
2.1 计算参数
以国内某条地铁线路为背景展开研究,单洞单线隧道,盾构直径7.0 m,如表 2所列隧道和地铁A型车的具体参数.

表2 地铁列车与隧道基本参数Tab.2 Structural parameters of the train and tunnel
2.2 隧道坡型及坡度
1) 隧道坡型选择
研究V型坡、W型坡、人字坡、单面上坡和单面下坡五种常见的坡型,如图3所示,表示五种坡型的简单示意图,不同的坡型有峰值或峰谷,如图3中标注的红点位置.后续将不同坡型的峰值/峰谷统称为“变坡点”,人字坡、V型坡和W型坡分别以各自变坡点的个数将隧道总长均分,每段与水平面均呈θ角.
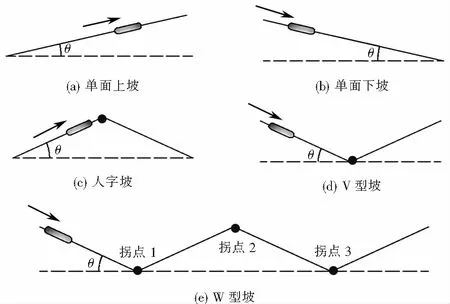
图3 五种坡型示意图Fig.3 Schematic sketch of slope style
2) 隧道坡度选择
根据规范[17]规定:地铁区间隧道的线路最小纵坡适宜采用3‰,而正线的最大纵坡宜采用30‰.本文选取3‰、15‰和30‰三种坡度展开研究.
3) 压力监控点位置
扰动波在隧道内传播一定距离后,呈一维特征,本文在数值过程中,将隧道等效为一条线,不同点表征不同断面的压力.从隧道入口端开始每间隔378 m均匀设置1个点提取压力,共计20个,本文后续将数值模拟的压力提取点统称为压力监控点.
3 结果与分析
3.1 坡型对隧道压力的影响
研究坡型对隧道压力的影响时,坡度取30‰,取距隧道入口端3 780 m处监控点来分析.如图4所示,垂直于横坐标的红/绿实线表示压缩波通过监控点时刻;红/绿虚线表示膨胀波通过监控点时刻;黑色实/虚线分别表示车头/尾鼻尖通过监控点时刻.A和A′分别为车头和车尾驶入隧道入口端产生的初始压缩波和膨胀波,B和C为初始膨胀坡和压缩波在隧道端口反射得到的压缩波,B′和C′分别为初始压缩波和膨胀波在隧道端口反射得到的膨胀波.考虑列车实际上/下行运营模式,所以本文后续将单面上/下坡放一起考虑.
由图4可知:隧道坡型不同,导致同一监控点的压力时间历程曲线差别较大,监控点位于隧道中部,其刚好是人字坡、V型坡和W型坡(变坡点2)的变坡点.监控点压力在前期的变化随着坡型的不同而有所差异:对于无坡度、单面上坡和单面下坡这三种情况,当车头驶入隧道入口端后,由于空气向前流动未受到任何阻碍,所以前期三种情况下的压力时间历程曲线是重合在一起并基本保持为零.对于人字坡,当车头驶入隧道入口端后,隧道内的空气便沿着上坡面向上流动,到达变坡点后又迅速的沿下坡面向下流动,这就使得监控点一直维持为负压值,且随着列车的驶入而增大,直到初始压缩波传播到监控点时压力值骤升.对于V型坡,当车头驶入隧道入口端后,隧道内的空气沿着下坡面向下流动,直到初始压缩波到达监控点时压力值骤升.对于W型坡,分析方法同上,在前期出现“先降后升”是由于在监控点之前存在变坡点1.由图4可知:隧道中部监控点的最大正压值出现在初始膨胀波传播到监控点前的某一时刻,最大负压值一般出现在车尾通过监控点瞬间,导致不同坡型下中部监控点得到的最大正、负压值也就不同.
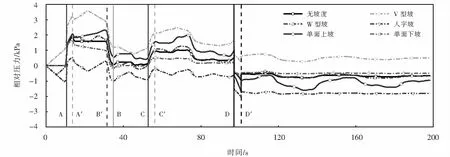
图4 距隧道入口端3 780 m处监控点的压力时间历程曲线Fig.4 Time history curve of pressure at the point 3 780 meters away from the entrance of the tunnel
为定量分析坡型对隧道监控点的相对压力最大值的影响,如图5所示,给出隧道坡度为30‰时,隧道内各监控点在不同坡型下的相对压力的最大正、负压值.由图5可知:最大正压值的最大值和最小值分别出现在V型坡和人字坡隧道,且监控点均距隧道入口端3 780 m;最大负压值的最大值出现在单面上坡隧道,监控点距隧道出口端378 m,最大负压值的最小值出现在V型坡隧道,监控点均距隧道入口端3 780 m;平直隧道和单面下坡隧道各监控点的最大正压值相比其它坡型的小,且变化不大.

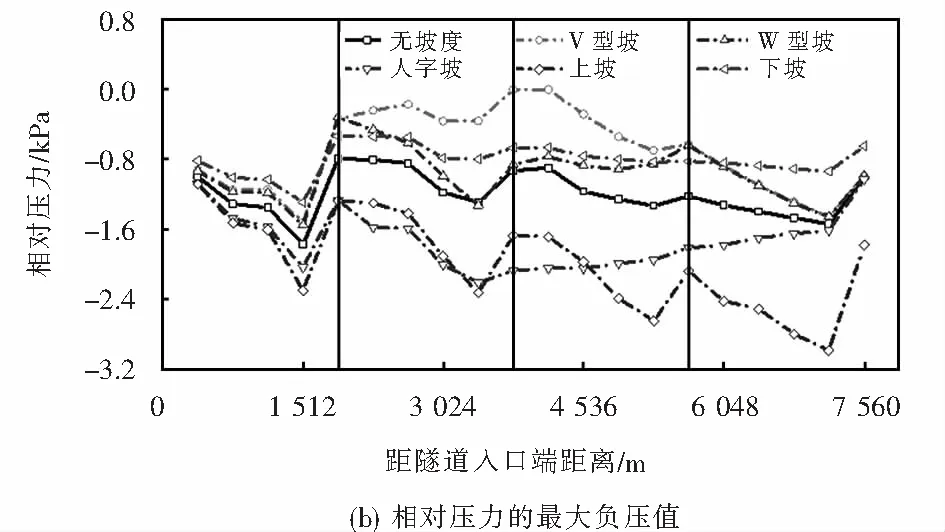
图5 隧道内监控点在不同坡型下相对压力的最大值Fig.5 Maximum pressure values of the different points under different gradients
3.2 坡度对隧道压力的影响
研究坡度对隧道压力的影响,以W型坡隧道为例分析.如图6所示,给出了距隧道入口端3 780 m处的监控点在不同坡度下的压力随时间历程曲线.由图6可知:相比于隧道坡型,坡度对隧道监控点的压力较小.
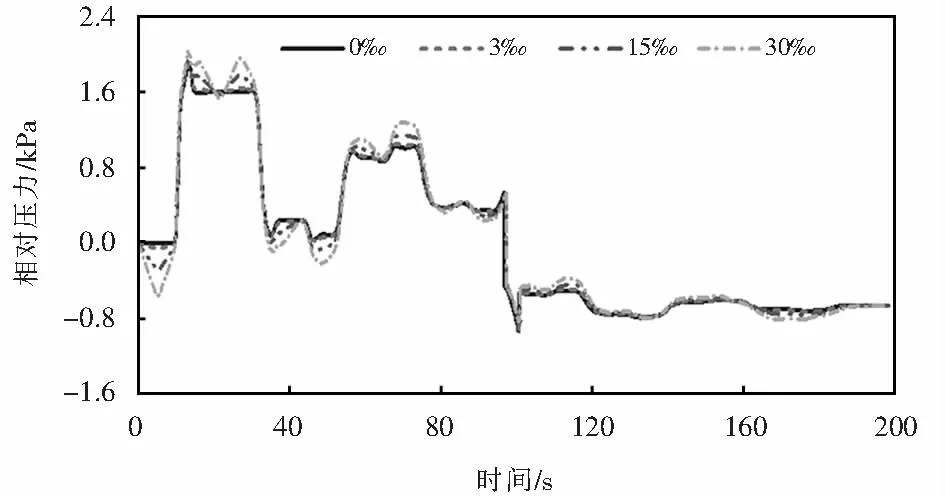
图6 不同坡度下监控点压力时间历程曲线Fig.6 Time history curve of pressure at monitoring points at different gradients
为深入分析坡度对隧道监控点压力的影响,如图7~8所示,分别给出不同坡型隧道内20个压力监控点在不同坡度下的最大正、负压值.由图7和图8可知:对于单面上坡、V型坡和W型坡隧道各监控点的最大正压值随着坡度的增大而增大,单面下坡和人字坡隧道反之;单面上坡和人字坡隧道各监控点的最大负压值随着坡度的增大而增大,单面下坡、V型坡和W型坡隧道反之.

图7 隧道压力监控点在不同坡度下相对压力的最大正压值Fig.7 Maximum positive pressure values at monitoring points under different gradients
为定量分析坡度对各隧道的压力影响,如图9所示,给出了不同坡型隧道在各坡度下20个压力监控点相对压力的最大正、负压值的最大值.由图9可知:隧道坡度为30‰时,单面下坡的最大正压值最小为1.891 kPa,V型坡的最大正压值最大为3.581 kPa;单面下坡的最大负压值最小为-1.285 kPa,单面上坡的最大负压值最大为-2.985 kPa.
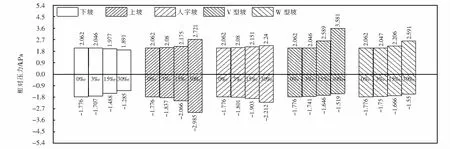
图9 各坡型隧道在不同坡度下相对压力的最大正、负压力值Fig.9 Maximum pressure values of each slope tunnel under different gradients
4 结论
本文以国内某条地铁线路为背景,基于一维可压缩非定常不等熵流动模型的广义黎曼变量特征线法,研究了地铁A型车以140 km/h的速度通过7 560 m隧道时,五种坡型,三种坡度对隧道压力的影响,得出以下结论:
1) 单面上坡、V型坡和W型坡隧道最大正压值随着坡度的增大而增大,单面下坡和人字坡隧道反之;单面上坡和人字坡隧道最大负压值随着坡度的增大而增大,单面下坡、V型坡和W型坡隧道反之.
2) 在距单面上/下坡隧道端口1 512 m处监控到最大压力值;在距平直隧道和人字坡隧道端口378 m处监控到大压力值;在距V型坡隧道端口3 780 m处监控到最大压力值;在距W型坡隧道端口1 890 m处监控到最大压力值.
3) 最大正压值的最大值出现在坡度为30‰的V型坡隧道,且距隧道端口3 780 m;最大负压值的最大值出现在坡度为30‰的单面上坡隧道,且距端口7 182 m.
4) 从压力波的角度考虑,建议V型坡隧道中部位置不布置附属设施,单面上/下坡和人字坡隧道端口位置不布置附属设施,W型坡隧道距隧道端口1 890 m处不布置附属设施.
