多复变差分Clunie型定理
2021-07-16武王宁曹廷彬
武王宁,曹廷彬
(南昌大学数学系,江西 南昌 330031)
1 引言与主要结果
首先介绍一些多复变的Nevanlinna理论的相关定义。
令z=(z1,…,zm)∈m,‖z‖2=
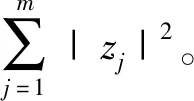
Bm(r):={z∈m:‖z‖ 1962年,Clunie[1]得到了如下引理:如果w(z)是复平面上的一个亚纯函数使得微分方程 wnP(z,w)=Q(z,w) 成立,其中n∈,P(z,w)和Q(z,w)是系数为亚纯函数的关于w(z)和w′(z)的多项式且degQ(z,w)≤n。那么 m(r,P(z,w))=O(logr+logT(r,w)+T(r)) 其中r→∞除去有限个线性测度集合,T(r)是P(z,w)和Q(z,w)的系数的特征函数的最大值。这个结果在复微分方程的值分布研究中是一个很重要的工具,之后许多学者在此基础上进行了推广[2-8]。2006年,Halburd-Korhonen[9]证明了上述Clunie引理的差分版本(即P(z,w)和Q(z,w)是系数为亚纯函数的差分多项式且w(z)是有穷级的亚纯函数),可以用于研究差分方程[10-11]的值分布问题。Laine-Yang[12]随后将其推广得到了更一般的结果:令w(z)是上的一个有穷级为ρ=ρ(w)的亚纯函数且使得微分方程 U(z,w)P(z,w)=Q(z,w) 成立,其中U(z,w),P(z,w)和Q(z,w)是关于w(z)和w(z+c1),w(z+c2),…,w(z+ck)的差分多项式且degU(z,w)=n,degQ(z,w)≤n。如果U(z,w),P(z,w)和Q(z,w)的系数为关于w(z)的小函数且U(z,w)只包含最大总次数的一项。那么对于任意的ε>0, m(r,P(z,w))=O(rρ-1+ε)+ο(T((r,w))) 其中r→∞除去有限个对数测度集合。虽然此定理覆盖了很多方程,但不适用于差分Painlevé Ⅳ方程。为此,Korhonen[13]证明了一个新的差分Clunie型定理可以包含差分Painlevé Ⅳ方程。最近,Cao-Xu[14]把Laine-Yang[12]的差分版本的Clunie定理从单复变推广到了多复变。为此,我们考虑是否可以把Korhonen[13]得到的新的差分Clunie型定理从单复变推广到多复变。 定义复偏差分多项式如下: w(z+cm)λm (1.1) 其中aλ(z)关于m上的一个亚纯函数w(z)的小函数,ci∈m{0}(i=1,…,m),I是一个有限的多指标集合。P(z,w)在w(z)和w(z+ci)(i=1,…,m)的总次数记为degw(P),P(z,x0,x1,…,xm)在x0=0处关于变量x0的零点的阶记为ord0(P)。定义P(z,w)的权为κ(P)= P(z,w)=w(z)3+w(z+1)w(z)2 degw(P)=3,ord0(P)=2,κ(P)=1。如果(1.1)中每一项的次数dλ=λ0+…+λn是非零且各项总次数均相同,则称P(z,w)是齐次多项式。 我们采用[13]中相同方法,得到了如下两个定理: 定理1令w(z)是m上的一个亚纯函数且使得 H(z,w)P(z,w)=Q(z,w) 成立,其中P(z,w)是一个系数为亚纯函数的齐次偏差分多项式,H(z,w)和Q(z,w)是系数为w(z)函数的关于w(z)的多项式且没有公因子。如果 max{degw(H),degw(Q)-degw(P)}> min{degw(P),ord0(Q)}-ord0(P) 那么 N(r,w)≠ο(T((r,w))) 定理2令w(z)是m上的一个亚纯函数且使得 H(z,w)P(z,w)=Q(z,w) 成立,其中P(z,w)是一个系数为亚纯函数的齐次偏差分多项式,H(z,w)和Q(z,w)是系数为亚纯函数的关于w(z)的多项式且没有公因子。如果 2κ(P)≤max{degw(Q),degw(H)+degw(P)}-min{degw(P),ord0(Q)} 那么 m(r,w)=o(T(r,w))+O(T(r)) 引理1[14]令f(z)是m上的一个亚纯函数且那么对于所有的c∈m{0},我们有 o(T(r,f)) T(r)≤T(r+Φδ(r))≤ 根据上述引理,Cao-Xu[14]得到了N(r,f(z))和N(r+L,f(z))之间的关系,在我们定理的证明中起到了至关重要的作用。 引理3[14]令f(z)是m上的一个亚纯函数且那么对于所有的与r无关且大于0的常数L,我们有 N(r+L,f(z))=N(r,f)+o(N(r,f)) 引理4[16]令f(z)是m上的一个非常数亚纯函数,假设 首先我们假设N(r,w)=ο(T((r,w)))。在(1.1)式中令L=maxj=1,…,m{||cj||},由引理3我们可以得到 ord0(P))N(r+L,w)=(degw(P)- ord0(P))N(r,w)+ο(T((r,w)))=ο(T((r,w))) 根据引理4,有 ord0(P))T(r,w)+ο(T((r,w))) 所以 (3.1) 另一方面,因为P(z,w)是一个齐次的偏差分多项式,所以由引理1可得 (3.2) (3.3) 其中dw=max{degw(Q),degw(H)+degw(P)}-min{degw(P),ord0(Q)} (3.4) 结合(3.2),(3.3),考虑假设条件 max{degw(H),degw(Q)-degw(P)}>min{degw(P),ord0(Q)}-ord0(P) 便有 在(1.1)中令L=maxj=1,…,m{‖cj‖},则由引理3有 另一方面,在定理1的证明中,由(3.2)和(3.3)可知 结合上面两式以及假设 2κ(P)≤max{degw(Q),degw(H)+ degw(P)}-min{degw(P),ord0(Q)}=dw 可得对于任意的r∉E2∪E3,m(r,w)=o(T(r,w))+O(T(r))。


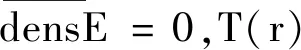
2 引理
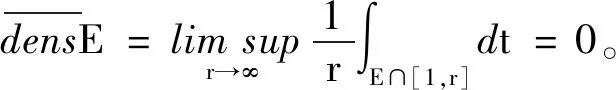



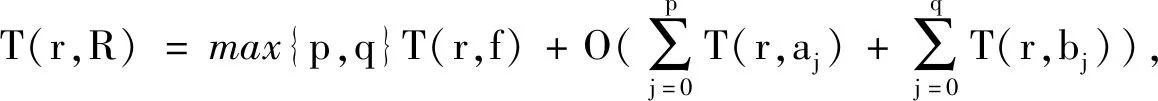
3 定理的证明
3.1 定理1的证明

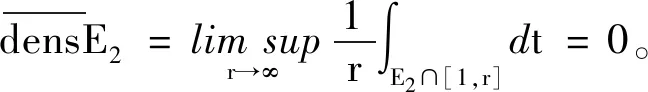
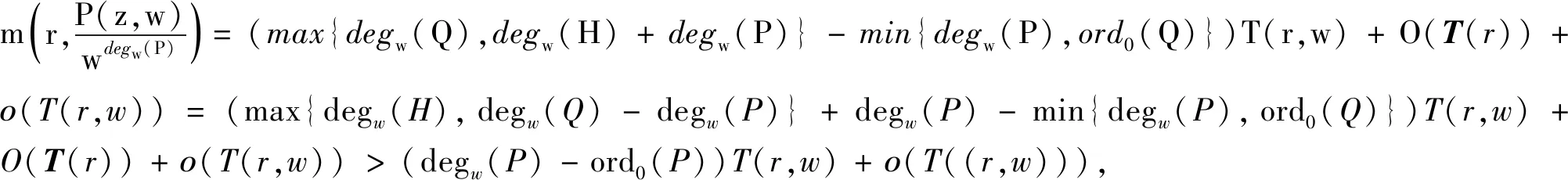
3.2 定理2的证明