基于合成平均刺激的平均表征机制 *<br/>——来自平均面孔吸引力的证据

基于合成平均刺激的平均表征机制 *
——来自平均面孔吸引力的证据

2021-07-16田欣然侯文霞欧玉晓陈文锋尚俊辰

心理学报 2021年7期

田欣然侯文霞欧玉晓易冰陈文锋尚俊辰

(1 中国人民大学心理学系,北京 100872) (2 东南大学人文学院医学人文学系,南京 211189)

1 引言

我们的视觉系统每时每刻接收到海量信息,这些信息很多是高度结构化的。这些结构化的信息彼此相似,以集合的形式存在。人们可以对这些集合进行知觉平均(perceptual averaging),相当精确地抽取集合内所有成员的平均表征(average representation,Alvarez,2011;Haberman &Whitney,2012;Whitney &Leib,2018),涉及大小、方向、明度、位置等低水平特征(Alvarez &Oliva,2008;Ariely,2001;Bauer,2009;Parkes et al.,2001),也包括面孔身份、性别和表情等高级社会性信息(Haberman &Whitney,2007;Haberman et al.,2015;Li et al.,2016)。很多研究关注大脑中平均表征是如何产生的：是通过整合集合成员来形成一个平均刺激的表征还是通过个体成员特征的平均值(mean value)计算来完成平均任务(Maule &Franklin,2015;Whitney &Leib,2018)。以往研究中,平均表征通常是用集合成员的平均值来作为测量指标,隐含了平均表征等同于集合成员平均值的假设。然而,由于集合平均刺激的特征值和成员特征值的平均往往十分相似而难以区分,这种假设并不能作为证据来区分平均表征的产生是由于大脑中形成平均刺激的表征还是由于集合成员的平均值计算。因此,平均表征的形成机制仍然是一个有待解决的问题。解决这个问题的一个思路就是分离集合平均刺激的特征值和集合各成员特征值的平均,而平均面孔由于其吸引力通常都比合成平均面孔的成员吸引力平均值更高(Carragher et al.,2018;Komori et al.,2009),很适合作为这个问题解决的切入点。为了有效区分平均刺激的表征和平均值计算的混淆问题,本研究通过利用集合面孔吸引力的平均表征和集合中所有面孔的吸引力平均值的差异性来考察知觉平均过程中是否形成了平均刺激的表征。

1.1 平均表征形成机制的争议

已往研究对平均表征的形成方式提出了两种主要解释,即基于分布式注意的整体编码和基于聚焦注意的个体编码。整体编码观点认为,视觉系统对集合刺激进行平行加工,因而被试能够准确表征集合平均值,却不能够对集合内的个体进行准确表征(Ariely,2001)。个体编码观点则认为,视觉系统将有限的注意资源集中在从集合中抽取的少数样本上,并对其进行精细加工,然后通过样本信息的平均值计算来推断集合的平均表征(de Fockert &Marchant,2008;Myczek &Simons,2008)。

从一般视觉加工的角度看,视觉信息的加工是分层级的。关于整体编码和个体编码的争论某种程度上可以归结为在平均表征形成过程中整体和个体的视觉加工层级优先性。最近,视觉加工的逆层级理论(reverse hierarchy theory,Hochstein &Ahissar,2002;Hochstein et al.,2015)认为整体加工和个体加工存在着逆层级性,即统计表征作为一种由自下而上的快速过程构建的高水平表征优先于个体表征的觉察。逆层级理论认为,整体表征(如场景主旨gist)的意识知觉从高级皮层开始,是一种基于低级皮层输入的知觉过程;在视觉加工开始阶段,我们仅能有意识觉察到视觉场景的整体表征(如gist),不能觉察到高水平整体表征的前因细节(antecedents,即构成整体表征的个体细节);在这个优先的层级加工后,视觉系统才将注意导向到特定的低级皮层处理单元,提取局部细节信息,即在高级皮层的整体表征以自上而下的方式返回到局部加工(逆层级返回,reverse hierarchy return)以证实(或矫正)初步的整体表征估计值(Hochstein et al.,2015)。因此,根据逆层级理论可以推论,平均表征最先是大脑整合粗略的个体信息形成的,并非基于精确个体表征的平均计算;但在加工后期会受到个体表征的矫正。然而,这仅仅是个推论,有待更直接的证据证实。

1.2 集合吸引力高评现象和平均面孔吸引力

和表情、身份等其他面孔特征类似,学者也曾经推测面孔集合平均吸引力应等于每张面孔吸引力的平均值(Abbas &Duchaine,2008;Brady &Alvarez,2015;Haberman &Whitney,2012)。早期研究发现,由3 个不同吸引力水平的年轻男性面孔组成的集合的吸引力刚好等于3 个男性的平均吸引力(Anderson,1965;Anderson et al.,1973)。

然而,研究者也发现了不同的结果。van Osch等人(2015)系统地操纵了集合的容量大小,发现当集合中的面孔数量超过6 张,集合的吸引力评分要显著高于集合成员的评分的平均值。这被称为集合吸引力高评现象(group attractiveness effect)。小容量面孔集合在特定条件下也存在集合吸引力高评现象：例如Willis (1960)发现在集合只有2 张或3张面孔时,集合吸引力的评分要比成员的平均值更极端,高吸引力集合的评分会比成员平均评分更高。

van Osch 等人(2015)认为集合吸引力高评现象可能的机制是面孔集合的知觉加工形成了平均面孔的表征,即面孔集合的平均吸引力表征并不是成员吸引力数值的平均,而是被试将集合中的所有面孔加以变形(morph)加工并融合成新的平均面孔(average-face),从而影响集合面孔吸引力的评价。面孔吸引力与面孔平均性具有强相关(O’Toole et al.,1999;Rhodes et al.,2001),即平均面孔的吸引力会由于平均表征自身携带的平均属性而得到提升,进而高于组成它的所有面孔的吸引力平均值(Carragher et al.,2018)。

van Osch 等人(2015)关于平均面孔的解释符合刺激集合形成平均刺激的表征的观点,但并没有解释集合吸引力平均值(Anderson et al.,1973;Luo &Zhou,2018)和集合吸引力高评不一致的矛盾。我们认为这并不矛盾,Anderson 等(1973)的研究都采取了较小的面孔集合(

=3 或4),而高评结果出现于较大的集合(

≥ 8) (van Osch et al.,2015)。正是这种集合大小的差异可能引起不一致的结果：即相对于大集合面孔,集合较小时加工资源足以对个体成员精确加工,个体成员表征更突显,更容易干扰平均面孔表征。Li 等人(2016)的发现为这个观点提供了支持证据：在有限的加工资源下,平均表征相对于个体的表征具有优势性,个体表征的精确度较低;但如果加工资源比较充足,个体表征精确度上升,而平均表征的精确度则降低。根据逆层级理论,平均表征的形成不需要精确的个体表征,而数值的计算需要建立在较高的个体表征精确度之上。此外,平均面孔的吸引力也受集合面孔数量的影响,即小容量集合面孔合成的平均面孔吸引力也低于大集合合成的平均面孔(Langlois &Roggman,1990)。事实上,van Osch 等(2015)也发现,当集合容量减少,高评现象出现的概率大幅下降。这可能是由于小容量集合形成的平均面孔吸引力相对不高或者平均面孔受到干扰,也可能是没有形成平均面孔而依赖于平均值计算。因此,小容量集合面孔吸引力的高评现象会减少,但其机制有待厘清。

1.3 问题提出和假设

目前集合平均表征的形成机制仍然停留在理论层面,尚未有直接的证据。合成平均刺激作为一种可能的机制,能够较好地解释集合表征加工相关的理论问题和实验现象。首先,为平均表征的整体编码和个体编码之争提供解决思路;其次,为视觉加工的逆层级理论提供实证支持;最后,为集合面孔吸引力的高评现象提供实证解释。本研究使用平均辨别任务(实验1 和2,mean discrimination paradigm,Haberman &Whitney,2009)和吸引力评价任务(实验3 和4),通过比较集合吸引力和平均面孔的吸引力探讨集合吸引力高评现象的机制,以进一步厘清知觉平均过程中是否形成了平均刺激的表征。平均辨别任务要求被试对单个刺激与集合平均表征进行知觉比较,用知觉比较后对集合平均表征的反应作为因变量来推断平均表征是否存在。吸引力评价任务要求被试对集合整体和平均刺激进行评价,直接反映平均表征的知觉过程。我们设置了集合中包含平均面孔的条件,如果集合加工中形成了平均面孔,那么集合原本有无平均面孔对结果将没有影响;如果没有形成平均面孔,那么集合包含平均面孔将促进平均辨别过程或是提升集合吸引力。实验1 和3 通过比较在大容量集合中包含或不包含平均面孔刺激这两种条件下按键的比例来为集合平均面孔的形成提供更直接的证据,实验2 和4 通过比较不同集合容量中集合平均面孔与集合吸引力的关系是否发生变化来为平均表征的形成和平均值计算的争议提供实验数据支持。此外,通过扩散模型分析结果探究集合加工过程,为实验1 和2 提供信息加工过程方面的证据。根据平均表征形成机制的不同观点,可以对实验的结果有如下预测：

(1)如果平均表征是通过集合成员的吸引力平均值计算,那么由于平均面孔的高吸引力,包含平均面孔刺激的集合会比不包含平均面孔刺激的集合吸引力更高,更接近平均面孔吸引力,从而当集合包含平均面孔,集合吸引力会提高(实验3 和4),在平均辨别任务中判断集合吸引力更高的倾向增加,判断探测刺激平均面孔吸引力更高的比例降低,并且不受集合大小的影响(实验1 和2)。

(2)如果平均表征是通过形成平均刺激的表征来产生,那么集合中是否包含平均面孔刺激对平均辨别任务和评分任务没有影响(实验1 和3),并且在平均面孔受干扰的小集合中,包含平均面孔刺激的集合吸引力更接近平均面孔吸引力(实验4),从而判断探测刺激平均面孔吸引力更高的比例降低(实验2)。

(3)在假设2 的基础上,如果小集合平均面孔受干扰是高评现象减少的原因,那么在个体表征较为突出的情况下,集合吸引力和平均面孔吸引力的差异在不包含平均面孔刺激的集合条件下更大(实验4),进而,小集合判断探测刺激平均面孔吸引力更高的比例在不包含平均面孔刺激的集合条件下更高(实验2)。

(4)如果小集合平均面孔吸引力相对大集合而言较低是高评现象减少的原因,那么小集合中平均面孔吸引力下降导致集合吸引力和平均面孔的差异更小(实验3 和实验4 对比),进而,小集合判断探测刺激平均面孔吸引力更高的比例更低(实验1 和实验2 对比)。

2 实验1：大容量面孔集合加工中是否形成平均面孔

实验1 通过平均辨别任务,要求被试选择集合吸引力和平均面孔吸引力之间较高的一个,操纵集合中是否出现平均面孔,进而判断平均面孔是否形成。

2.1 方法

2.1.1 被试

采用GPower 以统计功效power=0.8,中等效应量

=0.25 和重复测量2 (自变量集合类型：2 个水平)为参数估计的最小样本量为

=34。实际招募中国人民大学在校生34 名(其中18 名女性),平均年龄20.75 岁,标准差2.02 岁,右利手,视力或矫正视力正常。本研究中所有被试均签署知情同意书,实验得到了中国人民大学心理学系伦理委员会的批准。

2.1.2 实验材料

为了产生足够的组间差异,选取了互联网材料作为吸引力极高和极低的面孔图片,去除头发、脖子和耳朵,将面部轮廓剪成椭圆形,并转换成灰度图像来进行标准化。部分面孔材料选自中国化面孔情绪图片系统(王妍,罗跃嘉,2005)中的女性–中性情绪库。中国化面孔情绪图片系统中选取的图片与互联网材料共同组成原始材料。所有材料都经过20名中国大学生在吸引力水平和情绪效价(均为101点量表评分)上的评分(10 名女性,平均年龄为20.54 岁,标准差2.17 岁),其中被评价为非中性(与评分50 有显著差异)的材料被剔除。选定的材料效价评分(

=49.94,

=0.77)与中性(评分50)没有显著差异,

(19)=0.35,

=0.732。评定后选择的原始面孔30 张,其中包含6 张互联网材料(其中4 张属于高吸引力组,2 张低吸引力组),其余24 张图片从中国化面孔情绪图片库中选取。

随后,用面孔合成软件 Abrosoft FantaMorph (www.fantamorph.com)将不同面孔集合的平均面孔制作出来,共有365 张。该软件可以将两张面孔按照一定的比例融合,将面部各特征以众多关键点来标注,如嘴角的位置,大小,弧度,随后取关键点的平均值来合成图像。例如,当我们希望制作4 张原始面孔的平均面孔,就将原始面孔两两一组,再按照50:50 的比例进行合成取中,将合成的两张图片再次按照50:50 比例合成,就相当于每张原始面孔在合成面孔的贡献比例为25%,得到了4 张原始平均面孔的平均面孔。如果要制作3 张原始面孔的平均面孔,则控制每张面孔的贡献比例为33.3%即可。

所有的面孔图片再次经过20 名中国人民大学在校生的吸引力评定(10 名女性,平均年龄为20.35岁,标准差2.03 岁),作为事先评定的得分。

所有实验材料使用24 英寸的Dell 显示屏呈现,分辨率为1920×1080,灰色背景,被试直坐时双眼距离显示屏距离约为70 cm。

2.1.3 实验设计

采用单因素被试内设计,自变量为集合类型(无平均面孔的集合G1 vs.有平均面孔的集合G2),因变量为判断平均面孔吸引力更高的比例和扩散模型分析得到的反应决策指标(信息累积速率v、阈限差值a 和非决策加工时长t0,详见结果部分)。

2.1.4 实验程序

实验采用平均辨别任务,先呈现集合刺激,再呈现探测刺激。探测刺激为集合平均面孔、集合成员面孔、非成员非平均面孔。由于和平均面孔以及集合平均值的大小关系不确定,难以对结果进行推断,后两种刺激类型在本研究中只作为反应填充刺激(控制条件)。

在集合刺激类型上,使用12 张原始面孔组成集合,即是“不包含平均面孔的集合G1”水平,如果使用11 张原始面孔组成集合,并将集合成员的平均面孔作为新成员进入集合中,即是“包含平均面孔的集合G2”水平。包含平均面孔的集合中,平均面孔的位置随机呈现。在探测刺激类型上,呈现集合成员的平均面孔即是“集合平均面孔”水平,当集合刺激包含平均面孔时,相当于平均面孔出现两次;“呈现集合成员之一”的水平中,呈现集合中除了平均面孔以外的其他成员面孔之一;呈现集合刺激中没有出现过的面孔即是“新面孔”水平。

在每个试次中,被试首先注视中心点1000 ms,随后,他们看到呈现在屏幕上的集合刺激2000 ms,之后呈现空屏500 ms,随后呈现一张探测面孔,呈现到出现反应为止。要求被试按F 或J 键判断集合刺激的整体吸引力和探测刺激的个体吸引力哪个更高,共180 个试次,各个条件混合随机呈现,每60 个试次休息一次。在探测面孔为新面孔和集合成员之一两种条件下,一半探测刺激在预评中的吸引力高于集合刺激成员吸引力平均值,一半低于平均值(如图1)。

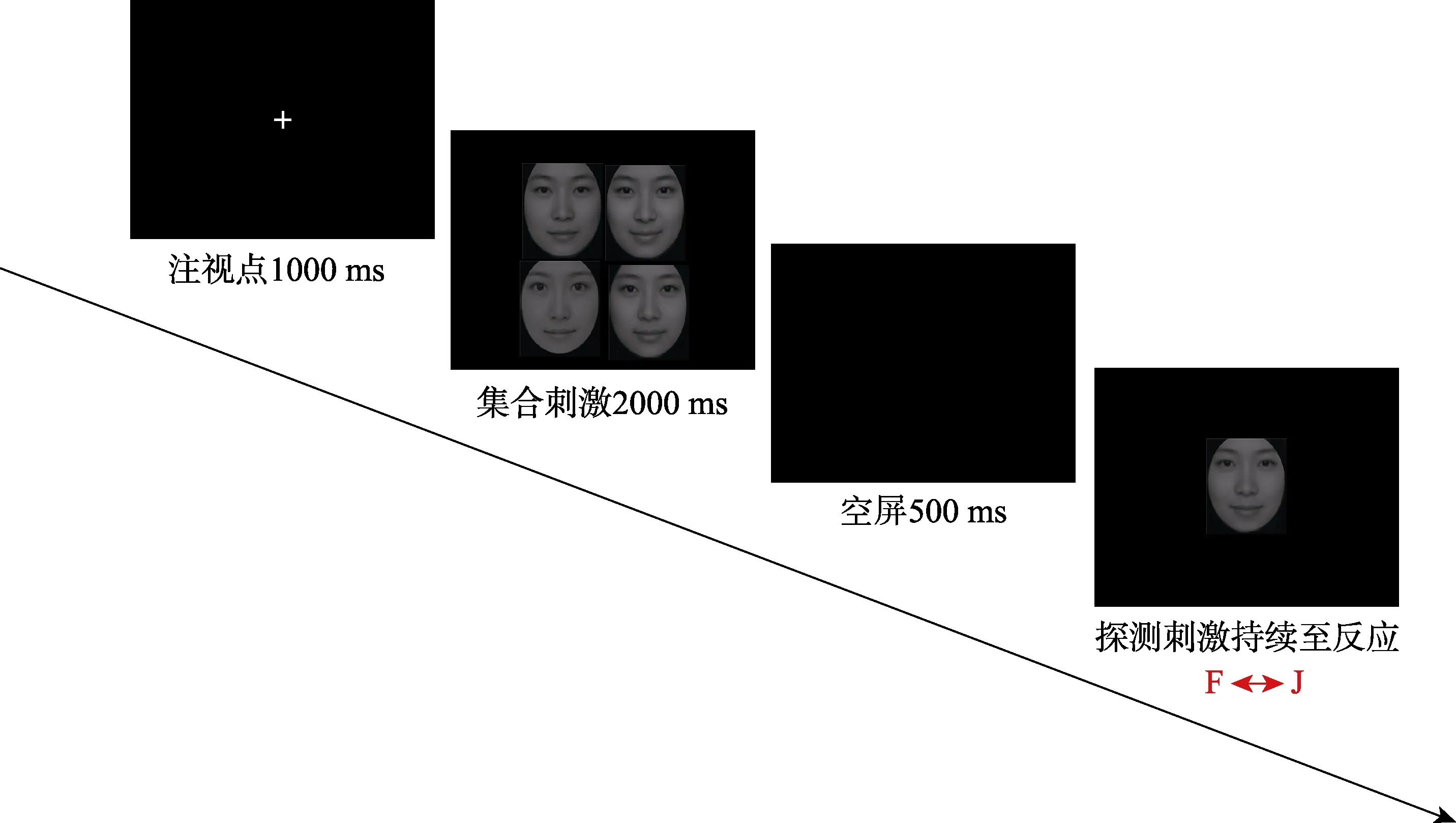
图1 实验1、2 流程图

集合刺激以4×3矩阵呈现,单张面孔图片的视角为5.69°×6.53°。探测刺激材料是一张单独的面孔,呈现在屏幕中央,图片尺寸与集合成员刺激尺寸一致。

2.1.5 扩散模型

根据逆层级理论,平均面孔的形成尽管快速,但仍然需要信息累积,因而有可能在包含和不包含平均面孔的集合之间产生决策反应差异。为了考察这种可能的差异,我们分析了反应决策信息,采用扩散模型(the diffusion model;Ratcliff,1978;Ratcliff &McKoon,2008) 将不同的认知过程进行分解,综合利用反应时分布与反应准确性结果,进一步分析包含和不包含平均面孔对集合面孔吸引力的知觉

机制。该模型可以将分解的认知过程对应到不同的模型参数中(Voss et al.,2013)。

扩散模型的基本假设是：在快速的二选一任务中,信息从起始点不断累积直到达到某反应的阈限标准后激活反应。基本扩散模型(Ratcliff,1978)有4个参数(如图2),分别为：

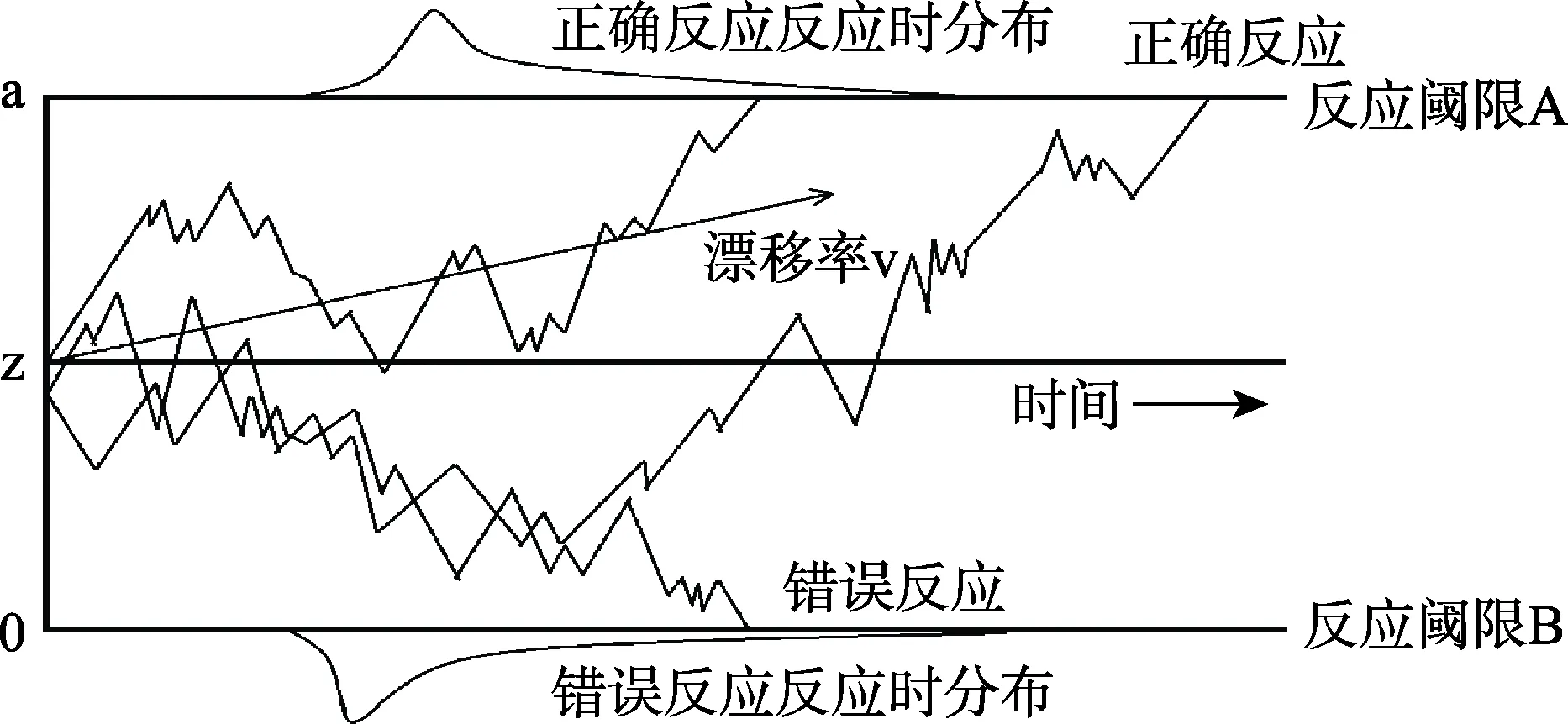
图2 扩散模型(翻译自Ratcliff &McKoon,2008,Figure 2)。图中展示了扩散模型的3 条路径样例。信息从起始点(z)以平均速率(v)开始逐渐累积,直到达到反应A 的阈限(a)或反应B 的阈限(0)。由于随机噪音,这些路径在每个试次之间都有所变异。

1)漂移率(drift rate),记为v,表明信息累积的速率;

2)阈限差值(threshold separation),记为a,表明做决策所需要的信息量;

3)起始点(starting point),记为z,表明决策前的预先偏向;

4)非决策加工时长(duration of nondecisional processes),记为t0,包含编码、反应执行等非决策的时间。

2.2 结果

2.2.1 按键反应结果

我们根据预评吸引力分数计算了在探测刺激类型为控制条件刺激的反应正确率,以此确定被试进行了充分理解和正确反应,同时验证事先评定的吸引力评分是否适用于本实验的被试。根据预评分数计算集合成员的吸引力平均值,再和预评的探测面孔吸引力比较来确定正确反应,结果表明探测刺激类型为新面孔和集合成员之一两种条件下的总正确率达到84.72%,远高于随机反应,

(33)=28.21,

＜ 0.001,95% CI=[0.32,0.37],Cohen’s

=9.82。说明被试的吸引力判断和事先评定基本一致。根据事先评定的得分,我们分别统计了实验1 中不含平均面孔的集合中探测刺激为平均面孔的条件下所有集合成员吸引力的平均值

1=49.19,同时假设该集合合成了平均面孔并计算包含了该平均面孔的集合成员吸引力平均值,也就是假设生成了平均面孔并将其吸引力计算进集合的成员平均值

2=50.49。

1 和

2 的差异表明,合成平均面孔提高了集合吸引力平均值,

(19)=22.82,

＜ 0.001,95% CI=[1.14,1.37],Cohen’s

=10.47。我们统计了实际反应中判断探测刺激平均面孔吸引力更高的比例。无论集合中包含和不包含平均面孔,被试判断平均面孔吸引力更高的比例(不包含平均面孔G1：84.03%,包含平均面孔G2：83.55%)都显著高于随机概率(50%),

(33)=8.16,

＜ 0.001,95% CI=[0.25,0.42],Cohen’s

=2.84;

(33)=10.31,

＜ 0.001,95% CI=[0.27,0.40],Cohen’s

=3.59。当探测刺激为平均面孔,判断平均面孔吸引力更高的比例在包含平均面孔、不包含平均面孔的集合类型之间没有显著差异(如图3),

(33)=0.11,

0.912,95% CI=[–0.10,0.11],表明有无平均面孔对集合吸引力的知觉辨别没有显著影响。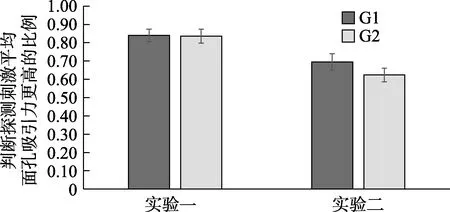

图3 不同条件下被试判断平均面孔吸引力更高的比例

2.2.2 扩散模型分析

前述比例分析虽然表明有无平均面孔对集合吸引力的知觉辨别没有显著影响,但并不清楚对辨别决策过程(如辨别时间、决策标准等)有无影响。这里我们采用层级扩散模型方法(the hierarchical diffusion model,HDM;Vandekerckhove et al.,2011)进行数据的模型拟合。HDM 分析的优势在于在模型参数计算时考虑被试之间的个体差异。此外模型上下限分别设定为正确反应和错误反应,在探测刺激为平均面孔条件时,将判断探测刺激吸引力更高设定为正确反应。由于对于正确和错误反应不存在预先的反应偏向,因此模型将起始点(z)设置为a/2。模型的其他参数设定为随研究变量(集合类型,探测刺激类型)变化。通过层级扩散模型拟合,最终得到每个被试在每个条件下的漂移率v,阈限差值a和非决策加工时长t0,并进行统计检验分析(如图4)。

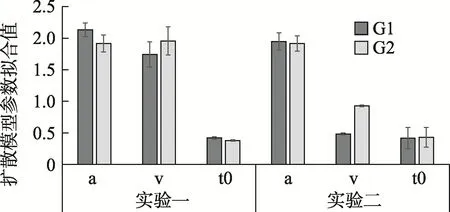
图4 实验1、实验2 获得的层级扩散模型拟合结果

扩散模型是对每个被试进行单独拟合,一般认为,如果模型拟合优度参数Rhat 小于1.05 (Vehtari et al.,2021),则拟合度较优,我们对实验1 的拟合结果进行单样本

检验发现,各拟合参数(

=1.00)均显著小于1.05,表明模型拟合良好。以模型参数为因变量的

检验表明,在信息累积漂移率v 和阈限差值a 上,集合是否包含平均面孔没有显著差异,

(33)=0.48,

0.632;

(33)=1.72,

0.096。这表明其不影响对集合吸引力和平均面孔的辨别;但非决策加工时长t0 受到了集合是否包含平均面孔条件的影响,集合包含平均面孔条件所需的t0 更短,

(33)=2.57,

0.015,95% CI=[0.01,0.06],Cohen’s

=0.90。

2.3 讨论

实验1 的结果表明,容量为12 的集合面孔吸引力确实存在高评现象。这种高评现象来自合成平均面孔的更高吸引力,并影响了被试对集合吸引力和探测刺激平均面孔的比较,使得与实际包含平均面孔的集合条件结果没有差异。实验结果模式符合假设2 的合成平均刺激,不支持假设1 的平均值计算。因此,平均辨别并不是简单地通过计算集合原有成员的平均值,而是形成了集合平均面孔。由于平均面孔的高吸引力,有平均面孔集合所有成员的平均值高于无平均面孔的集合的成员平均值,更接近探测刺激平均面孔,从而探测刺激和集合吸引力更不易区分。因而,如果是根据平均值计算来完成平均辨别任务(即成员平均值是比较标准),故而有平均面孔条件下判断平均面孔吸引力更高的比例将低于无平均面孔条件。但是,结果与此预测相反,判断平均面孔吸引力更高的比例在包含平均面孔、不包含平均面孔的集合类型之间没有显著差异。因此,更可能的是,人们在知觉集合刺激时将成员合成为一张新面孔(即具有高吸引力的平均面孔),从而对不包含平均面孔的集合吸引力造成显著的提高;而在包含平均面孔的条件中,整个集合形成的平均面孔应该等同于其中的11 张原始面孔形成的平均面孔,也就是集合中已经出现的这张平均面孔。那么平均面孔出现在集合中就不应当对集合吸引力造成显著的提高;故包含/不包含平均面孔的条件中选择集合整体吸引力更高的比例不存在差异。

情景2：中美间贸易摩擦进一步升级的情形。即美国从2018年四季度起对合计2500亿美元中国输美商品加征25%关税、2019年起对全部中国输美商品一律加征25%关税；对此，中国相应地从2018年四季度起对合计1100亿美元自美进口商品加征25%关税，并于2019年起对全部自美进口商品一律加征25%关税。

扩散模型分析结果表明,在没有实际平均面孔的输入时,编码加工等非决策时间更长,这说明平均辨别任务过程中形成平均面孔需要加工时间和资源的投入。这个过程是很快的(约400 ms),因而对决策影响不大,从而决策信息累积速度与有实际平均面孔输入时没有显著差异。

总结而言,实验1 的结果表明集合吸引力的判断过程形成了平均面孔,从而导致集合吸引力高评。那么,有什么因素会影响平均面孔的形成呢？近期研究发现,高级特征如面孔表情的平均表征是个容量有限的过程(Ji et al.,2018),受到加工资源的制约(Li et al.,2016)。那么,面孔吸引力的平均表征是否也受到容量的影响？从以往的结果看,答案似乎是肯定的。例如,van Osch (2015)发现,在集合容量为4～6 的集合中,集合吸引力高评现象出现的可能性很低。以往发现面孔集合吸引力相当于成员平均值的研究也都采用的是较小的集合(Anderson,1965;Anderson et al.,1973)。这是否说明小容量集合中没有平均面孔形成,小集合面孔吸引力判断存在与大容量集合不同的机制？但还存在另外一种可能,即平均面孔确实形成了但受到干扰。为了分离这两种可能,实验2 考察了小容量集合吸引力与平均面孔的关系。

3 实验2：集合容量对面孔集合加工的影响

实验2 采用4 张面孔组成的集合,采用与实验1 相同的实验设计和程序,考察了容量对集合吸引力与平均面孔的关系的影响。

3.1 方法

3.1.1 被试

采用GPower 以统计功效power=0.8,中等效应量

=0.25 和重复测量2(自变量集合类型：无平均面孔的集合G1 vs.有平均面孔的集合G2)为参数估计的最小样本量为

=34。实际招募中国人民大学在校生35 名大学生,排除一名记错按键方向的被试,有效被试34 名(17 名女性),平均年龄20.68岁,标准差2.27 岁,右利手,视力或矫正视力正常。

3.1.2 实验材料

与实验1 相同,但集合刺激只包含4 张图片。在集合刺激类型上,使用4 张原始面孔组成集合,即是“不包含平均面孔的集合G1”水平,如果使用3张原始面孔组成集合,并将集合成员的平均面孔作为新成员进入集合中,即是“包含平均面孔的集合G2”水平。探测刺激类型包括集合平均面孔、集合成员面孔、非成员非平均面孔,探测刺激的后两种刺激类型是控制条件刺激。

集合刺激以 2×2 矩阵呈现,图片的尺寸为8.19° × 9.43°。探测刺激材料是一张单独的面孔,呈现在屏幕中央,图片尺寸与集合刺激尺寸一致。

和实验1 相同。每个被试在主任务完成后还对每张图片进行了吸引力评分。

3.1.4 实验程序

与实验1 相同。

3.2 结果

3.2.1 按键反应结果

根据事先评定的得分,在探测刺激类型为新面孔和集合成员两种条件下的反应正确率为84.17%,显著高于随机水平,

(33)=16.84,

＜ 0.001,95% CI=[0.31,0.39],Cohen’s

=5.83,以此确定被试确实充分理解和正确反应。与实验1 相似,分别统计了探测刺激为平均面孔的条件下不含平均面孔的集合中所有成员吸引力的平均值

1=47.82,同时也假设该集合生成了平均面孔并计算包含了该平均面孔的成员均值

2=49.73。

1 和

2 的差异表明,平均面孔也同样提高了小容量集合吸引力平均值,

(29)=6.68,

＜ 0.001,95% CI=[1.44,2.47],Cohen’s

=2.48。根据被试主任务后的评定,发现平均面孔的吸引力(

=55.18,

=11.02)高于集合成员面孔吸引力的平均值(

=51.71,

=11.76),

(33)=2.35,

=0.020,95% CI=[0.51,7.05],Cohen’s

=0.820。对实验2 和实验1 中平均面孔为探测刺激条件下的平均面孔吸引力进行比较,结果表明小集合面孔形成的平均面孔吸引力更低,57.20 vs.65.61,校正

(41.7)=100.61,

＜

0.001,95% CI=[8.26,8.60],Cohen’s

=24.53。对实验2 和实验1 中平均面孔(探测刺激)和集合平均值的差值(9.51 vs.16.43)进行跨实验比较,发现实验2 小集合平均面孔和集合平均值的差异更小,校正

(53.8)=112.13,

p <

0.001,95% CI=[6.70,6.94],Cohen’s

=27.53。因而,小集合中判断探测刺激平均面孔吸引力更高的比例将下降。结果确实如此,实验2 中判断平均面孔吸引力更高的比例显著低于实验1 (66.57% vs.83.79%),校正

(63)=3.37,

001,95% CI=[0.07,0.27],Cohen’s

=0.85。统计检验结果表明,被试倾向于认为平均面孔的吸引力要高于集合的吸引力。判断探测刺激平均面孔吸引力更高的比例显著高于随机概率,

(33)=4.60,

＜ 0.001,95% CI=[0.09,0.24],Cohen’s

=1.60。而且对于判断平均面孔吸引力更高的比例,集合中不包含平均面孔的条件显著高于包含平均面孔的条件,

(33)=3.77,

=0.001,95% CI=[0.03,0.12],Cohen’s

=1.31 (如图3)。由此可见,小集合的加工结果确实与大集合不同,为了探究这种差异的存在是由于加工机制不同还是平均面孔受到干扰,我们对不含平均面孔的集合中是否形成了平均面孔进行了检验。我们通过匹配选择出与平均面孔吸引力接近的新面孔探测刺激,两类面孔的吸引力均值分别为54.80 vs 54.11,

(46)=0.18,

=0.859,但探测刺激为平均面孔时探测刺激吸引力被判断为更高的比例(69.12%)仍然高于新面孔条件(52.01%),

(33)=4.84,

＜ 0.001,95% CI=[10.21%,24.88%],Cohen’s

=1.69。即使进一步匹配选择出比平均面孔吸引力更高的新面孔刺激(72.33 vs.60.86,

(42)=3.85,

＜ 0.001,95% CI=[5.54%,17.49%],Cohen’s

=1.19),探测刺激为平均面孔时探测刺激吸引力被判断为更高的比例(71.01%)仍然高于新面孔条件(61.31%),

(33)=2.62,

=0.013,95% CI=[2.24%,17.13%],Cohen’s

=0.91。这说明在辨别过程中平均面孔并不是作为新面孔出现的,而更可能是集合呈现时形成了平均面孔。

3.2.2 扩散模型分析

实验2 同样通过层级扩散模型拟合,最终得到每个被试在每个条件下的漂移率v,阈限差值a 和非决策加工时长t0,并进行统计检验分析。各拟合参数(

=1.00)均显著小于1.05,表明模型拟合良好。以模型参数为因变量的

检验表明,在阈限差值a 和非决策加工时长t0 上,集合是否包含平均面孔对集合吸引力和平均面孔的辨别没有影响,

(32)=–0.63,

=0.533,

(32)=0.72,

0.095;但信息累积漂移率v 受到了集合是否包含平均面孔条件的影响,集合不包含平均面孔条件的信息累积更慢,

(33)=–4.775,

＜ 0.001,95% CI=[–0.63,–0.25],Cohen’s

=1.66 (如图4)。

3.3 讨论

实验2 发现,在不包含平均面孔的条件中,判断平均面孔吸引力更高的比例显著高于包含平均面孔的条件,说明平均面孔出现在集合中,显著地增加了集合的整体吸引力。由此可见,当集合容量为4,被试主观形成的平均面孔表征被抑制或者没有形成。如果是平均面孔表征没有形成,则平均面孔作为探测刺激应该和新面孔类似,但分析表明平均面孔和新面孔的探测结果完全不同。因而,小集合面孔也形成了平均面孔。这些结果模式符合合成平均刺激的假设2,不支持平均值计算的假设1。

尽管小集合面孔形成了平均面孔,但平均辨别的反应模式和实验1 大集合并不相同。这可能是因为小集合中形成的平均面孔更容易受干扰,因而包含平均面孔刺激的集合吸引力更接近平均面孔,从而判断平均面孔吸引力更高的比例降低。这也反映在被试的反应决策参数上,决策所需的信息累积速度相对实验1 更慢,所需的加工时间更长。扩散模型的结果表明,在有实际平均面孔的输入时,辨别决策将更容易,表现为决策信息累积更快。这些结果说明平均辨别任务过程中形成了平均面孔,只是受到了干扰。这种干扰还体现在小集合判断平均面孔吸引力更高的比例比实验1 更低。实验结果表明,这可能来自两个原因：一是小集合平均面孔受干扰(假设3),那么集合吸引力和平均面孔的差异在不包含平均面孔刺激的集合条件下更大,从而小集合判断平均面孔吸引力更高的比例在不包含平均面孔刺激的集合条件下更高;二是小集合平均面孔吸引力更低,集合和平均面孔的差异更小(假设4)。

实验1 和实验2 的结果来自于相对间接的平均辨别任务。为了提供更直接的证据,实验3 和实验4 采用评分任务对实验1 和实验2 的结果进行进一步验证。

4 实验3：大容量面孔集合的评分

实验3 采用大容量面孔集合进行评分任务。为不同容量下集合吸引力和平均吸引力的关系提供更直观的证据。

4.1 方法

4.1.1 被试

采用GPower 以统计功效power=0.8,中等效应量

=0.25 和单因素5 水平(评分类型：不包含平均面孔的集合的成员均值

1、不包含物理平均面孔集合但将平均面孔计算在内的成员均值

2、不包含平均面孔的集合G1、包含平均面孔的集合G2、平均面孔Avg)为参数估计的最小样本量为

=21。实际招募中国人民大学在校生29 名大学生,有效被试29 名(15 名女性),平均年龄22.14 岁,标准差3.17 岁,右利手,视力或矫正视力正常。

4.1.2 实验材料

实验刺激与实验1 相同。

集合刺激包含12 张面孔,集合刺激以4×3 矩阵呈现,单张面孔图片的视角为5.69° × 6.53°。

在评分类型上,使用12 张原始面孔组成集合,即是“不包含平均面孔集合”水平;如果使用11 张原始面孔组成集合,并将集合成员的平均面孔作为新成员进入集合中,即是“包含平均面孔集合”水平,将集合成员面孔和平均面孔再次进行单独评定,即为“单独评定”水平。

4.1.3 实验设计

采用单因素5 水平(评分类型：不包含平均面孔的集合的成员均值

1、不包含物理平均面孔集合但将平均面孔计算在内的成员均值

2、不包含平均面孔的集合G1、包含平均面孔的集合G2、平均面孔Avg)的被试内设计。因变量为被试对目标集合或目标面孔的吸引力评分。

4.1.4 实验程序

实验流程如图5 所示。首先呈现500 ms 注视点,而后在屏幕上呈现一组面孔或是一张单独面孔,被试要对目标的吸引力进行0～100 的评分,0 代表吸引力最低,100 代表吸引力最高。

图5 实验3、4 流程图

4.2 结果

由于单张面孔的评分任务中包含原始面孔也包含各个集合的平均面孔,因此我们随后使用单张面孔的评分来计算集合的吸引力平均值,计算不包含平均面孔集合条件下的集合成员评分均值,得到

1=47.31;再假设该集合生成了平均面孔从而计算包含了平均面孔的成员均值,得到

2=48.78。将

1、

2、不包含平均面孔条件的集合吸引力G1、包含平均面孔条件的集合吸引力G2 和平均面孔吸引力Avg 作为评分类型5 个水平进行方差分析。结果表明,评分类型主效应显著,

(4,112)=27.60,

＜ 0.001,ƞ=0.50。多重比较结果如下(如图6)：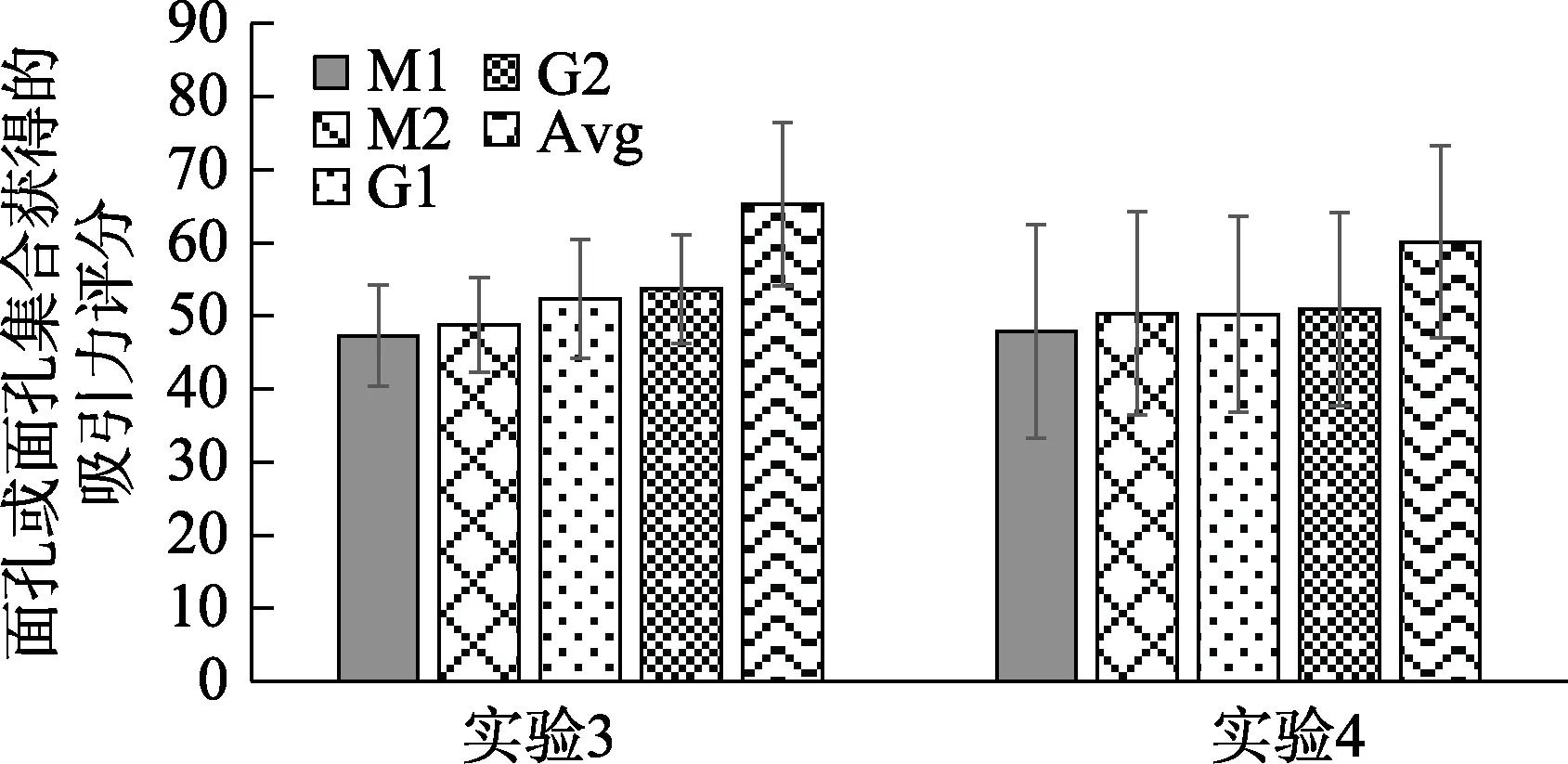

图6 实验3、4 吸引力评分结果

首先,

2 显著大于

＜ 0.001,95% CI=[1.22,1.71],再次确认了合成平均面孔对集合吸引力平均值的提升作用。其次,不包含平均面孔的集合吸引力评分G1 与包含平均的集合G2 差异不显著,

=0.532;与

2 差异不显著,

=0.053;但大于

=0.011,95% CI=[1.26,8.80]。第三,平均面孔吸引力显著高于整个集合的吸引力G1、G2 和成员平均值

1、

＜=0.001。趋势分析表明,从集合成员平均值、集合吸引力到平均面孔,存在着逐渐增加的趋势,

(1,28)=62.82,

＜ 0.001,ƞ=0.69。除此以外,我们也尝试了分析平均面孔和集合吸引力的差值,发现在包含或不包含平均面孔的集合间差值没有显著差异,

(28)=0.19,

=0.852,再次验证了实验1 中被试选择探测刺激平均面孔吸引力更高的比例在集合包含和不包含平均面孔条件下没有显著差异。

4.3 讨论

实验3 的评分任务结果基本重复了实验1 的结果。首先,在大容量集合中的评分任务验证了大容量集合的集合吸引力高评现象,即集合吸引力高于集合成员评分的平均值。其次,平均面孔吸引力大于集合吸引力,说明了实验1 中被试判断探测面孔吸引力更高的原因。第三,集合是否包含平均面孔,对于集合评分没有显著影响(支持假设2,不支持假设1);并且,不包含平均刺激的集合评分G1 只有在考虑了生成平均面孔条件下才接近集合成员平均值,即

2。最后,趋势分析和多重比较结果表明,不包含平均刺激的集合评分更接近于包含平均面孔条件的结果。这些结果说明大容量集合确实生成了平均面孔。

5 实验4：小容量面孔集合的评分

实验4 采用小容量面孔集合进行评分任务,为不同容量下集合吸引力和平均吸引力的关系提供更直观的证据。

5.1 方法

5.1.1 被试

采用GPower 以统计功效power=0.8,中等效应量

=0.25 和单因素5 水平(评分类型：不包含平均面孔的集合的成员均值

1、不包含物理平均面孔集合但将平均面孔计算在内的成员均值

2、不包含平均面孔的集合G1、包含平均面孔的集合G2、平均面孔Avg)为参数估计的最小样本量为

=21。实际招募中国人民大学在校生31 名大学生,剔除一名评分全距小于10 的被试,有效被试30 名(15名女性),平均年龄21.39 岁,标准差2.46 岁,右利手,视力或矫正视力正常。

5.1.2 实验材料

实验刺激与实验1 实验2 相同。

集合刺激包含4 张图片,集合刺激以2×2 矩阵呈现。当评价类型为集合平均面孔,刺激呈现在屏幕中央,单张面孔图片的视角为5.69° × 6.53°。

在评分类型上,使用4 张原始面孔组成集合,即是“不包含平均面孔集合”水平;如果使用3 张原始面孔组成集合,并将集合成员的平均面孔作为新成员进入集合中,即是“包含平均面孔集合”水平,将集合成员面孔和平均面孔再次进行单独评定,即为“单独评定”水平。

5.1.3 实验设计与程序

与实验3 相同。

5.2 结果

与实验3 类似,使用单张面孔的评分来计算集合的吸引力平均值,计算不包含平均面孔集合条件下的集合成员评分均值,得到

1=47.87;再假设该集合生成了平均面孔从而计算包含了平均面孔的成员均值,得到

2=50.32。将

1、

2、不包含平均面孔条件的集合吸引力G1、包含平均面孔条件的集合吸引力G2 和平均面孔吸引力Avg 作为评分类型5 个水平进行方差分析。结果表明(如图6),评分类型主效应显著,

(4,116)=6.27,

＜ 0.001,ƞ=0.18。多重比较结果如下：首先,

2 显著大于

＜ 0.001,95% CI=[1.82,3.08],再次确认了合成平均面孔对集合吸引力平均值的提升作用。其次,不包含平均面孔的集合吸引力评分G1 与包含平均的集合G2 差异不显著,

=0.110;与

2 差异不显著,

=0.977,与

1的差异也不显著,

=0.504。第三,平均面孔吸引力显著高于整个集合的吸引力G1、G2 和成员平均值

1、

≤ 0.007。此外,趋势分析表明,从集合成员平均值、集合吸引力到平均面孔,存在着逐渐增加的趋势,

(1,29)=21.05,

＜ 0.001,ƞ=0.42。除此以外,集合平均面孔和集合整体吸引力的差值,不包含平均面孔集合条件大于包含平均面孔集合的条件(9.90 vs.3.64),

(29)=6.40,

＜ 0.001,95% CI=[4.26,8.26],Cohen’s

=2.38,可以更直观地印证实验2 的包含平均面孔条件下中“被试判断探测刺激吸引力更高的比例降低了”这一结果。对实验4 和实验3 中的平均面孔吸引力进行比较,结果表明小集合面孔形成的平均面孔吸引力更低,60.11 vs.65.24,

=0.004,95% CI=[2.76,13.85],Cohen's

=0.94。对实验4 和实验3 中平均面孔和集合平均值的差值(6.76 vs.12.55)进行跨实验比较,发现存在一种可能的趋势,即实验4 的小集合中平均面孔和集合成员平均值的差异更小,校正

(35.649)=1.72,

=0.094,95% CI=[–1.06,12.81],Cohen's

=0.07。

5.3 讨论

实验4 的评分任务结果为实验2 的结果提供了直接的支持。首先,在小容量集合中,集合吸引力高评现象减弱了,集合吸引力和集合成员评分平均值

2 都没有显著差异,结合实验3 结果,验证了前人结论：集合吸引力高评现象在大容量集合强,在小容量集合弱。这符合平均面孔在小集合中更易受干扰的假设。此外,小容量集合的平均面孔吸引力确实下降,和集合平均值的差异更小,因而小集合平均面孔吸引力相对大集合而言较低也是高评现象减少的一个可能原因。其次,实验4 中,类似于实验3 的结果,集合是否包含平均面孔对于集合评分没有显著影响(支持假设2,不支持假设1);并且不包含平均刺激的集合评分G1 也和平均面孔计算在内的集合成员平均值

2 没有差异。趋势分析和多重比较结果表明,不包含平均刺激的集合评分更接近于包含平均面孔条件的结果。这些结果说明小容量集合也可能受到了生成的平均面孔的影响。此外,集合吸引力和平均面孔吸引力的差异在不包含平均面孔刺激的集合条件下更大(假设3),这反映了包含平均面孔刺激的集合吸引力更接近平均面孔吸引力,更直观地说明了在较小容量的集合中,被试主观形成的平均面孔表征被抑制(结合实验2 结果),也说明了为何在实验2 的包含平均面孔条件下中,被试判断探测刺激吸引力更高的比例降低了。

6 综合讨论

实验1、2 的按键反应和扩散模型拟合结果和实验3、4 的评分结果共同说明,当集合容量为12张,高吸引力的平均面孔是否出现不影响集合吸引力评分和平均辨别任务,说明表征集合时形成了集合平均面孔;当集合容量为4 张,平均面孔效应减弱了,可能是由于集合平均面孔的吸引力较低以及平均面孔被个体表征干扰了。

6.1 集合面孔吸引力高评现象

在van Osch 等人(2015)的研究中,通过采用给若干名女性拍摄的自然材料(如聚会照片)评分来探究集合吸引力,则发现了在较大的集合(人数较多的照片)中存在集合吸引力高于集合成员吸引力平均值的情况。

实验1 的平均辨别任务发现,当集合不包含平均面孔时,判断探测刺激吸引力更高的比例与包含平均面孔时相似,说明两种条件的平均吸引力相近,不包含平均面孔的集合吸引力高于成员面孔的平均值,从另一个角度反映了集合吸引力高评现象。实验3 则直接再次验证了大容量集合的集合吸引力高评现象。

实验4 的评分结果说明集合吸引力高评现象较弱。而实验2 正确率分析表明,实验2 也出现了集合吸引力高评现象,只是实验1 更明显。类似地,在van Osch 等人(2015)的研究中,较小的集合也很少观察到集合吸引力高于成员吸引力平均值。在本研究中,既有直接通过评分获得集合面孔吸引力高评现象的直接证据,也有借助平均面孔在集合中的作用大小来推测的部分。van Osch 等人(2015)研究中使用的是生态效度较高的自然材料,存在成员吸引力分布集中,缺少具有代表性的高低吸引力面孔的问题。本研究则改用了没有背景,由单独评分的面孔素材组成的集合,并平衡不同吸引力水平的面孔数量,依旧得到了类似的结论,说明在大容量集合中集合吸引力高评现象是比较稳定的,且现象的产生与集合平均面孔的形成有关。

6.2 平均表征的形成机制

通过将平均辨别的实际反应与不同理论假设的反应分布进行比较和拟合,我们发现集合吸引力包含平均面孔贡献的假设拟合更好,支持了平均表征过程中形成了平均刺激(如平均面孔)。在实验1中,集合包含平均面孔时,判断平均面孔吸引力更高的比例并未降低,说明包含或不包含平均面孔刺激的集合吸引力同等接近平均面孔,因此平均表征并不是通过集合成员的平均值计算得到的。类似的,无论还是实验3 还是实验4,都发现平均表征的吸引力要远高于集合成员的平均值。在实验2 的小集合中,发现新面孔作为探测刺激与平均面孔作为探测刺激的结果不同,则说明平均面孔作为探测刺激出现之前已经得到了加工。这个结论和近期Ying等人(2020)的结论一致,他们通过吸引力适应后效范式发现,由一组面孔引发的适应后效等于这一组的平均面孔引发的适应后效,同样支持了集合表征中存在平均刺激的形成。

值得注意的是,平均刺激的形成也需要资源投入,体现在实验1 没有平均面孔输入时需要更长的编码加工时间。Huang (2015)发现对于对象特征和统计表征,启动的效果是相等的,说明统计表征的形成至少需要和单个个体加工同等的注意资源。因此,平均表征和个体表征在早期可能是因此相互竞争的关系(Li et al,2016)。由于早期没有足够的认知资源加工所有个体,因此优先形成了平均表征。Bauer (2017)以不同长短的线条作为集合刺激,在平均辨别任务前加入数字记忆任务的研究发现,相比低记忆负荷条件(1 个0),高记忆负荷条件下(4～7个随机数字)更有利于形成平均表征。实验1 和实验2 的跨实验比较也发现,在小集合中整体信息积累速度也比大集合更慢。

与此同时,小集合同样形成了平均表征且需要资源的投入,表现在实验2 没有平均面孔输入时信息积累较慢。也就是说无论大小集合,都有平均刺激的形成。而大小集合之间的反应差异,是由于其他原因造成的,而不是出于不同的加工机制。

6.3 集合吸引力与平均面孔的关系

尽管集合吸引力表征中包含了平均面孔的贡献,但集合吸引力并不完全等同于平均面孔的吸引力。无论实验1 还是实验2,均发现被试倾向于评价平均面孔比集合吸引力更高的结果。并且实验3、4 平均面孔的评分也要高于集合的评分,说明集合吸引力是基于平均面孔的形成,将平均刺激纳入进来成为集合的成员,再对于集合进行整体评价。因此,集合吸引力高评现象并不完全如van Osch 等人(2015)所推断的仅依赖于平均面孔,而是与表情集合加工类似,读取平均面孔的表征(Haberman &Whitney,2009)。

类似的现象是,被试经常在再认任务中把平均表征误以为是集合中的成员,或者认为平均面孔与其中一个成员具有相同的身份(Neumann et al.,2013)。判断过程中被试可能使用了一种策略：在加工整个集合吸引力的时候,将平均面孔知觉成集合中某一成员,由于观察到集合中的其他面孔的吸引力多数低于平均面孔,进而倾向于认为单独出现的平均面孔的吸引力较高。

研究者曾发现,当存在多张面孔,单张面孔的吸引力会被判断得比孤立出现时更高(Walker &Vul,2014),并同样解释为平均的作用。背景面孔导致会将人脸的感知偏向群体的平均水平。因此,伴随同一目标面孔出现的背景面孔吸引力越高,目标面孔就会被评价得越高(Perrett et al.,1994;Walker &Vul,2014)。因此,平均面孔产生可能会对集合中的其他成员产生影响,由于平均面孔的吸引力高,导致集合其他成员的吸引力也得到了抬升。这是平均面孔对其他面孔产生的影响,也可能是集合吸引力高评现象产生的路径之一。

6.4 平均刺激表征与集合容量的关系

小容量集合中面孔吸引力一般会被评价与集合成员平均值相同(Anderson,1965;Anderson et al.,1973),且集合吸引力高评现象在小容量集合消失(van Osch et al.,2015),说明小容量的平均表征存在一些特异性。

一方面,小容量集合产生的平均面孔刺激的吸引力相对较低,可能因此导致对于集合吸引力的增加效果较小,因此集合吸引力高评现象减少。另一方面,可能是平均表征受到了干扰。逆层级理论提出(Hochstein et al.,2015),高级皮层的整体表征以自上而下的方式返回到局部加工,以局部细节信息证实(或矫正)初步的整体表征估计值,也就是说平均表征在加工后期会受到个体表征的矫正。Li 等人(2016)也发现,当呈现时间延长,认知资源增加,会导致个体表征的精度增强。

这两种理论均得到了本研究结果的支持,在实验2 中判断平均面孔吸引力更高的比例更低,以及实验4 中的平均面孔和集合吸引力差值比较结果表明小集合包含平均面孔的集合吸引力和平均面孔的差异更小,都说明小集合平均面孔吸引力较低在其中存在影响。与此同时,实验2 在包含平均面孔刺激时平均面孔吸引力更高的比例更低,说明相对于被试自己生成平均面孔刺激,直接输入平均面孔减少了集合吸引力和平均面孔之间的差异,支持小集合的平均面孔受到了干扰。在小集合中无论集合是否包含平均面孔,信息积累速度都比大集合更慢,也支持逆层级理论所说的局部细节信息对于整体表征的矫正和干扰。