基于自抗扰的多旋翼全姿态矢量控制方法
2021-07-15罗寓文朱玉玉
罗寓文, 朱玉玉
(西南科技大学 信息工程学院,四川 绵阳 621010)
0 引 言
由多旋翼为代表的小型无人机(unmanned aerial vehicle,UAV)在机器人领域内得到了大家的广泛关注。在传统的捷联惯导系统导航控制中,绝大多数的多旋翼姿态控制还是以欧拉角作为姿态环的被控对象分别控制偏航角、俯仰角、横滚角三个自由度。这种方法不可避免地忽略了欧拉角表示刚体旋转的奇异点也就是万向节死锁问题[1],由于欧拉角的万向节死锁问题,无人机在处于机头向上垂直姿态时其真实值没有明确的物理意义可言,对于欧拉角万向节死锁问题,文献[2~4]提出了基于四元数反馈的姿态控制方法,文献[5~8]提出了基于李群李代数的姿态控制方法。
本文将提出了一种基于方向余弦矩阵(DCM)姿态矢量的控制方法,避免使用欧拉角出现奇异值问题,实现了飞行器的全姿态控制,并在此基础上将无人机姿态内环角速度控制算法进一步改进为自抗扰控制(auto-disturbance rejection control,ADRC)技术[9~12],使用自抗扰控制技术中的微分跟踪器TD合理安排期望值过渡,避免了因控制器期望值发生大阶跃信号而引起控制器系统超调,扩张观测器ESO估计被控对象状态量与系统扰动。
1 全姿态矢量控制
对于姿态的表示,可以通过欧拉角、四元数、方向余弦矩阵DCM表示[13,14],而在姿态解算中方向余弦矩阵通常习惯用四元数来表示。本文提出的采用定义在北西天世界坐标系下的方向余弦矩阵DCM中的姿态矢量来实现飞行器全姿态控制。
1.1 表示出期望方向余弦矩阵
对于飞行器的姿态控制三个通道,期望值可以用欧拉角表示分别是Yaw,Pitch,Roll,同样的期望值也可以用方向余弦矩阵DCM1表示,公式如下
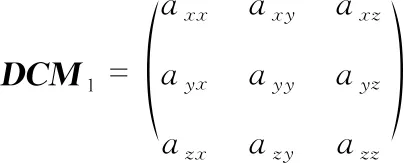
(1)
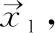
(2)
1.2 通过四元数表示出实际姿态方向余弦矩阵
在姿态解算中可以得到当前姿态四元数为q=(q0,q1,q2,q3)T,用四元数通过式(3)转换为当前姿态的方向余弦矩阵DCM2[15],世界坐标系为北西天,公式如下
(3)
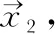
(4)
1.3 计算姿态外环控制器期望与反馈的误差
通过向量叉积的方式表示出三个姿态通道上的姿态误差ex,ey,ez公式如下
ex=xx+yx+zx,ey=xy+yy+zy,ez=xz+yz+zz
(5)
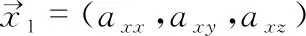
(6)
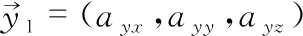
(7)
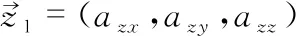
(8)
1.4 姿态外环控制率设计
对于多旋翼姿态外环来说,是一个一阶运动学方程
(9)
式中φ,θ,ψ为姿态三个通道,ωx,ωy,ωz为姿态对应的角速度三个通道,该公式为一个运动学模型,没有任何干扰,P控制器可以控制好系了,所以,姿态外环的控制率可以设计为
(10)
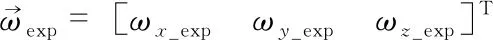
2 自抗扰控制技术的实现
本文把自抗扰控制技术中的微分跟踪器TD和扩张状态观测器ESO应用在多旋翼姿态控制的角速度环中。
2.1 微分跟踪器TD安排期望角速度值过渡
(11)
式中fh为微分跟踪器中间计算变量,fhan函数为微分跟踪器特有计算公式,r为可调参数跟踪速度,h为可调参数步长。
2.2 扩张状态观测器估计被控对象状态量与系统干扰
(12)
式中e为扩张状态观测器(ESO)中间计算变量,Z1为角速度状态估计量,Z2为角加速度状态估计量,Z3为系统扰动,β01,β02,β03为可调参数,b为可调参数补偿因子,h为可调参数步长。
2.3 姿态内环控制率设计
对于多旋翼姿态内环角速度环来说,是一个包含扰动的动力学方程
(13)

(14)
式中Kpω为P控制器可调参数,Kdω为D控制器可调参数。姿态内环控制完整的控制框图如图1所示。
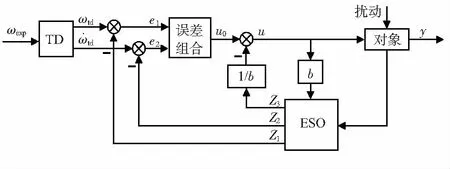
图1 完整的姿态内环控制框图
通过以上理论分析可以得出,此方法选取了姿态方向余弦矩阵(DCM)中的向量信息进行姿态控制,避免了使用欧拉角Yaw,Pitch,Roll进行姿态控制算法设计时存在算法奇异问题,真正从本质上解决了欧拉角万向节死锁问题。
3 实验结果分析
实验平台是开源PCB小型多旋翼无人机平台,其实物图片如图2。参数设置:起飞重量为38 g,单电机推力为15 g,电机个数为4个,机架轴距为130 mm,桨叶大小为46 mm。

图2 飞行器实物
在这个实验平台上,测量了一些飞行器重要的参数,如:单电机最大推力、电机推力与被控对象之前的关系等,来帮助整定控制器的参数,还在室内的环境中进行了真实的飞行实验测试,验证了此算法的工程应用,图3为飞行器在悬停状态下期望姿态与真实姿态之间的误差,可见最大横滚姿态和偏航姿态的误差都低于0.6°,而这个姿态误差在通常情况下是几乎无法用肉眼观察出来的。

图3 飞行中的姿态角度误差
4 结 论
本文研究的飞行器自抗扰全姿态矢量控制通过实物验证表明了此算法具有正确性和可靠性。通过大量的飞行测试与验证,本文所研究的新型姿态控制器能够实现。原则上只要飞行器飞行空间足够大,可以保证飞行器随手抛向空中时无论飞行器处于什么姿态,在空中解锁飞行器都可以回到水平正常飞行姿态,可以很好地完成复杂的多旋翼高机动飞行,并且从根本上解决了姿态控制使用欧拉角存在奇异值的问题。在保证控制算法具备可实施性的同时,又保证了控制算法的控制性能达到相应的指标要求。最后本文研究的飞行器控制算法性能视频同时被美国俄亥俄州克利夫兰州立大学(CSU)先进控制技术中心主任高志强教授收录于自抗扰控制技术网上频道。
