基于改进人工势场法的四旋翼无人机航迹规划算法
2021-07-15姜香菊
邓 叶, 姜香菊
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
0 引 言
航迹规划在四旋翼无人机高效与安全飞行中具有很重要的作用,它是指四旋翼无人机按照某种要求规划出一条从起始点到终止点最优或者次优的航迹,是四旋翼无人机研究领域的一个重要分支。目前常用的航迹规划方法包括:RRT算法[1]、粒子群算法[2]、蚁群算法[3,4]、人工蜂群算法[5]和人工势场法[6~9]等。其中人工势场法在航迹规划中具有比较成熟的应用,因其具有计算量小,规划速度快的特点。虽然人工势场法算法简便,但是也存在一些需要解决的问题,如目标不可达、振荡等问题。
文献[10]提出了增加垂直引导斥力解决了传统人工势场法的缺陷,并且比较和分析了人工势场、模糊逻辑和蚁群算法三种算法的性能,对于研究局部路径规划有很重要的参考价值。文献[11]为了解决极小值问题提出了“选择穿越法”,当四旋翼无人机陷入极小值状态时迅速激活该行为,使四旋翼无人机有选择性的穿越过障碍物,从而顺利的到达目标点。文献[12]对于复杂环境下的航迹规划问题,首先建立了栅格化环境模型,然后将蚁群算法和人工势场法结合,设计了环境感知因子,仿真结果表明了所提方法的有效性。文献[13]将稀疏A*搜索算法和改进的人工势场法相结合,应用在不同的障碍物所构成的威胁分布中,规划出了给定威胁指标下的最优路径,结果证明了其具有良好的动态规避性能。
四旋翼无人机在飞行过程中会受到很多因素的约束,本文在考虑了这些约束的条件下,首先以安全性为前提,提出了一种改进的人工势场法,即在斥力势场函数中加入了四旋翼无人机当下航迹点和目标点之间的距离,并且引入了协调力,在随机分布的障碍物环境和U型槽型障碍物环境下进行了仿真验证。
1 环境建模与约束条件
1.1 环境建模
假设四旋翼无人机的任务区域为正方形,并且以恒定的速度从起始点飞往目标点。不考虑任务区域的高度,将任务区域分为X和Y方向,进行m等分,则任务区域可以表示成由(m+1)个节点构成的栅格。在这些栅格内存在n个障碍物,四旋翼无人机在飞行的过程中需要避开这些障碍物,安全的到达目标点。
1.2 约束条件
1)最大曲率约束:由于四旋翼无人机自身机动性能的约束,不能在过小的转弯半径内改变航向,为了能使航迹满足无人机的各种条件要求,对得到的航迹需要进行曲线拟合,然后计算拟合曲线上各点是否满足四旋翼无人机的曲率要求,在不满足条件的情况下对规划的航迹进行平滑处理,直到满足需求为止[14]。假设四旋翼无人机飞行速度为v,最大曲率为kmax,四旋翼无人机的过载限制为n,则曲率与最小转弯半径Rmin之间满足的关系为
(1)
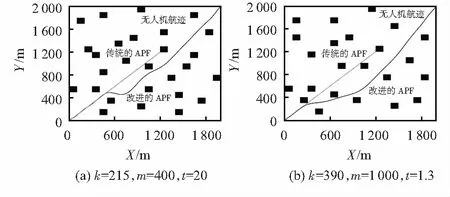
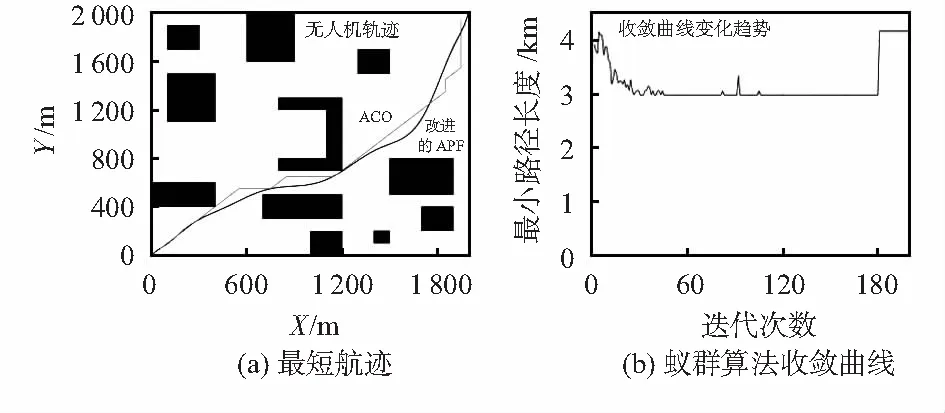
2)最大航程约束:受限于四旋翼无人机电量的约束,无人机必须在允许的最大航程和最长时间范围内完成任务,这就使得所规划的航迹要尽可能的短,该约束可以表示为L 航迹代价是用来评价四旋翼无人机航迹规划的优劣,在无人机实际飞行过程中面临的环境是复杂多样的,所以,应该多方面考虑各种因素对四旋翼无人机航迹的影响。假设不考虑四旋翼无人机飞行高度且在恒速的状态下飞行,为了能够缩短四旋翼无人机的飞行时间进而减少能量的消耗,航迹长度和避障是本文评价航迹优劣的两个考虑指标。为了方便分析不同航迹规划方法的优劣,这里引入代价函数 J=∑(w1Lij+w2fij) (2) 式中w1和w2分别为航迹代价和威胁代价的权重,fij为安全代价,用航迹在障碍物影响区域内的长度表示;Lij为航线段的欧氏距离,总和为航迹的总长度。 人工势场法是由Khatib提出的一种虚拟力法,该方法在目标点位置构造了虚拟的引力场,在障碍物位置构造了虚拟的斥力场。目标点对被控对象产生引力,障碍物对被控对象产生斥力。 假设四旋翼无人机的当前位置为X=(x,y),目标点的位置为Xg=(xg,yg)。则四旋翼无人机受到的引力场函数Uatt为 (3) 式中k为引力场增益。 四旋翼无人机受到的引力Fatt(X)为引力势场函数的负梯度 (4) 假设障碍物的位置坐标为Xo=(xo,yo),无人机到障碍物的距离为 ρ(X,Xo)=‖X-Xo‖ (5) 定义斥力势场函数为 (6) 式中m为斥力系数,ρo为障碍物的影响范围。由此斥力可定义为 (7) 人工势场法算法简单、实时性好,但是容易使四旋翼无人机陷入局部最小点的状态无法出来,难以到达目标点。 本文提出了一种改进的人工势场法,解决了四旋翼无人机无法到达目标点的问题[15]。在斥力势场函数中引入四旋翼无人机和目标点之间的距离,改进后的斥力势场函数如下 (8) 式中 (X-Xg)t=|(x-xg)t|+|(y-yg)t|为四旋翼无人机和目标点之间的相对距离,t为大于零的可变常数,一般的取值为2。则对应得到的斥力为 (9) 式中 (10) (11) 在实际的应用中通常采用它们的简化形式 (12) (13) 此外引入协调力 (14) 式中g为协调增益系数。 由此可以得到总的合力F(X)为 F(X)=Fatt(X)+Fre(X)+Fco(X) (15) 在利用改进的人工势场法得到航迹后,发现航迹存在一些不必要的航迹点,从而使得规划出来的航迹并不是最短的航迹。因此,可以进一步对航迹点进行裁减处理。航迹点裁减流程图如图1所示。 图1 航迹点裁减流程图 本文采用最小二乘法消除离散点,对采用改进人工势场法得到的航迹进行修正,主要针对航迹转弯角度较大和振荡的问题,通常四旋翼无人机的转弯角度限制在±90°范围内。对于拟合得到的新航迹需要分析是否符合航迹约束条件,若满足则采用修正好的航迹,若不满足则需要重新进行修正,直至满足航迹规划的约束要求。 为了验证所述改进算法的合理性,首先在MATLAB 2014b平台上进行了仿真,任务区域为20×20 的栅格环境,在不同的障碍物条件下的仿真结果如图2~图5所示。 图2是利用传统人工势场法和改进的人工势场法在两种随机分布的障碍物情况下规划的四旋翼无人机航迹,实线为传统的人工势场法得到的航迹,从图2中可以看出,在点(1300,1300)处四旋翼无人机陷入了局部最小,无法按计划到达目标点;虚线为采用了在斥力势场函数中加入了四旋翼无人机航迹点和目标点之间的距离同时引入协调力的方法所得到的航迹,改进后的算法使四旋翼无人机到达了设定的目标点。 图2 随机分布的障碍物 改进后的人工势场法参数设定为(a)k=215,m=400,t=20,总的航迹长度为2.950 8 km; (b)k=390,m=1 000,t=1.3,总的航迹长度为2.958 5 km。 1)U型槽向左 针对图3(a)所示的U型槽环境,改进的人工势场法设定的参数为k=390,m=800,t=9.17。设置蚁群算法参数为α=1,β=7,ρ=0.3,Q=1,M=50,K=100。 图3 U型槽向左时 2)U型槽向右 针对图4(a)所示的U型槽环境,改进的人工势场法设定的参数为k=500,m=1 000,t=11。设置蚁群算法参数为α=1,β=7,ρ=0.3,Q=1,M=50,K=100。 图4 U型槽向右时 3)U型槽向下 针对图5(a)所示的U型槽环境,改进的人工势场法设定的参数为k=200,m=500,t=10。设置蚁群算法参数为α=1,β=7,ρ=0.3,Q=1,M=50,K=100。 图5 U型槽向下时 图3(a),图4(a)和图5(a)得到的是分别采用改进的人工势场法和蚁群算法在三种不同的U型槽下的航迹,由于采用改进的人工势场法得到的航迹不够平滑,存在振荡和转弯角过大的情况,以上三幅图都是用了最小二乘法进行曲线平滑处理后得到的航迹。表1为采用不同方法得到的航迹长度对比。 表1 航迹长度对比 km 分析蚁群算法的收敛曲线图可以看出,当U型槽向右时即图4(b),算法具有很好的收敛性,在迭代到第22次时,蚂蚁就找到了最短路径。但如图3(b)所示,算法的收敛性不是很好,在找到最短路径后又出现了振荡,在迭代到第181次时,规划的路径变成了4.169 8 km,这与最开始收敛稳定规划好的航迹相比存在很大的差距,无法满足四旋翼无人机的最大航迹约束要求。从图5(b)可以看出在迭代到第52次时蚂蚁已经找到了最短路径为2.997 9 km,但是随着迭代次数的增加最小路径的长度不断变化,收敛曲线存在很严重的不稳定问题,虽然最终在第154次的时候趋于稳定,最小路径为4.028 4 km,但并不是最优路径。 比较两种算法能够看出,改进的人工势场法相比蚁群算法更具有稳定性,而且实时性更好,能够快速准确地规划出最优航迹,而蚁群算法耗时久、收敛性差难以在较短的时间内规划出一条最优航迹。 四旋翼无人机航迹规划在四旋翼无人机研究领域是一个重要的分支,本文针对四旋翼无人机航迹规划问题,提出了改进的人工势场法,解决了传统人工势场法出现的局部最小值问题。并且在栅格化的任务区域环境中,将改进的人工势场法和蚁群算法进行了对比,结果表明:改进的人工势场法能够快速高效地规划出最优航迹,使四旋翼无人机能够在最短的时间内避开障碍物,安全的到达目标点。1.3 航迹代价
2 改进的人工势场法
2.1 传统的人工势场法
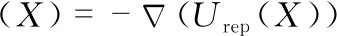
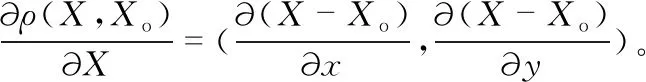
2.2 改进的人工势场法
3 航迹修正
3.1 航迹简化

3.2 航迹平滑
4 仿真结果与分析
4.1 随机分布的障碍物
4.2 三种不同的U型槽障碍物



5 结 论
