基于自抗扰控制的高超声速飞行器再入制导律

邵星灵，刘 俊，李东光

（1.中北大学仪器与电子学院，太原 030051；2.中北大学仪器科学与动态测试教育部重点实验室，太原 030051；3.中北大学机电工程学院，太原 030051）

1 引 言

近空间（也称临近空间）处于传统的空天之间，指的是高于常规航空器飞行范围并且低于轨道飞行器运行空间的空域，国际上将20～100 km的空域定义为近空间。近空间具有特殊的战略位置，上可威胁卫星等天基平台、下可攻击航空器等空基平台甚至地面目标，是未来战争中空天一体化作战的重要战略领域，并将对未来的作战思维产生重大而深远的影响[1-2]。

近空间高超声速飞行器是21世纪空天一体化技术飞速发展产生的新的战略制高点。由于飞行高度的优势，可避免目前绝大多数的地面攻击，生存力大大提高；由于飞行速度的巨大优势，可从本土出发在2 h内攻击全球任何目标而不需要海外基地；由于具备高超声速大范围机动能力，可轻易突破弹道导弹防御系统的拦截，突防能力大大提高。作为21世纪航空航天领域最受关注的研究方向，临近空间高超声速飞行器已逐渐成为各军事大国为争夺未来制空天权而竞相发展的热点。20世纪90年代以来，美国、俄罗斯、法国、德国、印度和澳大利亚等国陆续取得了高超声速飞行技术上的重大突破和重要进展，特别是美国已进行了多次相关飞行实验。

再入制导本质上是一个控制变量较少且约束强（包括过程和终端约束），但被控状态多（高度、速度、航程、横程等）的欠驱动时域优化问题，其主要任务是通过设计再入制导律实现纵向、横侧向的制导任务需求，确保再入过程的安全性和稳定性，同时为姿态控制系统提供标称制导指令。目前再入制导设计的思路主要有两类方法：标称轨迹制导和预测校正制导。对于预测校正制导而言，其主要存在预测过程中数值积分计算量大、难以保证数值迭代过程收敛性、无法解决过程约束等局限性[3]。对于标称轨迹制导，由于其采用离线轨迹优化与在线精确跟踪的制导策略，因此可较好地解决上述问题。为实现高精度的跟踪制导，已有大量控制方法得到应用，如二次型状态调节器[4]、滑模控制[5]、自适应[6]和鲁棒控制[7]，但已有方法的设计常依赖精确模型，难以抵挡再入过程气动参数摄动的不利影响，将直接导致跟踪精度不佳甚至制导任务失败。

本文研究高超声速飞行器再入制导律设计问题，应用反馈线性化技术将纵向平面制导任务转换为对高度和航程增广系统的控制描述，并设计倾侧角反转逻辑的切换机制以控制飞行器的侧向运动。

2 制导策略

高超声速飞行器再入段一般起始于高度70 km、20以上马赫数，结束于高度25 km、4马赫数左右。根据飞行能力可分为初始下滑段、准平衡滑翔段及快速俯冲段[8]。再入剖面具有如下特性：再入初期采用最大可用攻角飞行以满足热流约束，利用气动阻力减速，以快速通过高热流区；随高度降低，动压增大，气动升力增大，此时进入准平衡滑翔段，通过固定大攻角下滑以减小高度损失，该阶段持续时间较长；快速俯冲段或称精确打击段，为保证飞行器具有一定的下沉率，攻角指令较小。此外，出于结构热防护和配平的需要，再入攻角常设置为与速度相关的分段函数。因而，对于制导任务而言，再入全程仅需要确定倾侧角的控制规律，依靠改变升力方向进行大范围机动控制以满足纵向和横侧向制导精度的要求。

本文针对多约束条件及多种气动参数摄动影响的高超声速飞行器再入轨迹抗干扰跟踪问题，在标准轨迹制导方法的框架下，结合模型辅助线性自抗扰控制和基于航向角误差走廊的几何制导逻辑，提出了一种可满足纵向和横侧向平面制导任务需求的自抗扰再入制导律，实现三维再入轨迹快速跟踪并兼顾再入过程的安全性及终端控制的精度要求。

其主要思路为：首先，对于纵向制导，在描述高超声速飞行器纵向运动学模型的基础上，为提高再入终端高度和速度误差的可控性，引入航程参数和比例分配因子，将纵向高度和航程的加权视为被控输出量，把纵向平面制导任务转换为对高度和航程的增广系统的控制描述，从而在性能折衷的意义下解决纵向制导的欠驱动跟踪控制问题。其次，基于反馈线性化技术将增广纵向动力学系统输入输出线性化，将异于输入输出线性化系统标称模型的部分因素视为总不确定项，并构造模型辅助线性扩张状态观测器对总扰动进行实时观测并补偿，在此基础上，综合PD反馈控制律确定倾侧角幅值的更新规律；横侧向则基于航向角误差走廊的几何制导原理设计倾侧角反转逻辑的切换机制，控制飞行器的侧向运动。最后，通过纵向制导设计的倾侧角幅值指令和侧向生成的倾侧角符号综合形成倾侧角控制规律。相应的，基于自抗扰控制的再入制导律结构框图如图1所示。

图1 基于自抗扰控制的再入制导律结构框图Fig.1 Block diagram of Reentry Guide Law based on ADRC

2.1 纵向制导律设计

假设侧向轨迹控制可使飞行过程中瞬时平面与目标平面的夹角始终在小角度范围内，则纵向航程s与再入高度和速度满足：

引入比例分配因子a用以协调再入高度和航程跟踪的误差精度，以再入高度和航程的加权为被控输出量，定义y=H+a·s，则增广后的纵向运动学方程为

其中，速度通道和航迹倾角通道的参数化总不确定项dV及dθ分别为

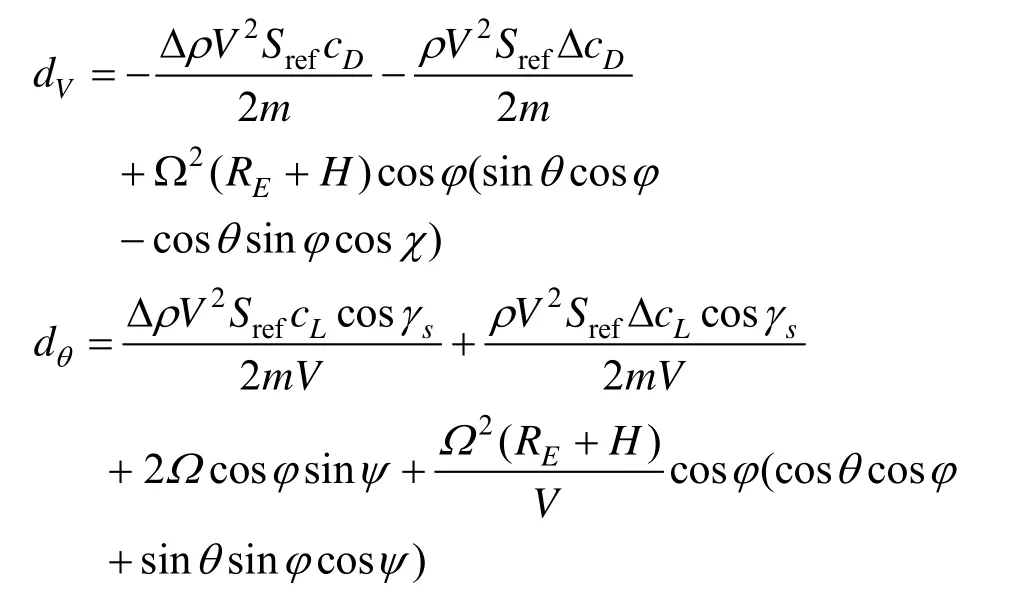
因此，纵向制导的任务可描述为：以cossγ为控制输入，以再入高度和航程的加权为被控输出，实现再入高度和航程的联合控制。

为明确被控输出和控制输入信号的传递动态，采用反馈线性化技术，对增广系统的输出量H+a·s关于时间求导直至出现控制量cossγ，从而实现面向控制器设计的被控对象输入输出线性化。具体的求导过程如下：

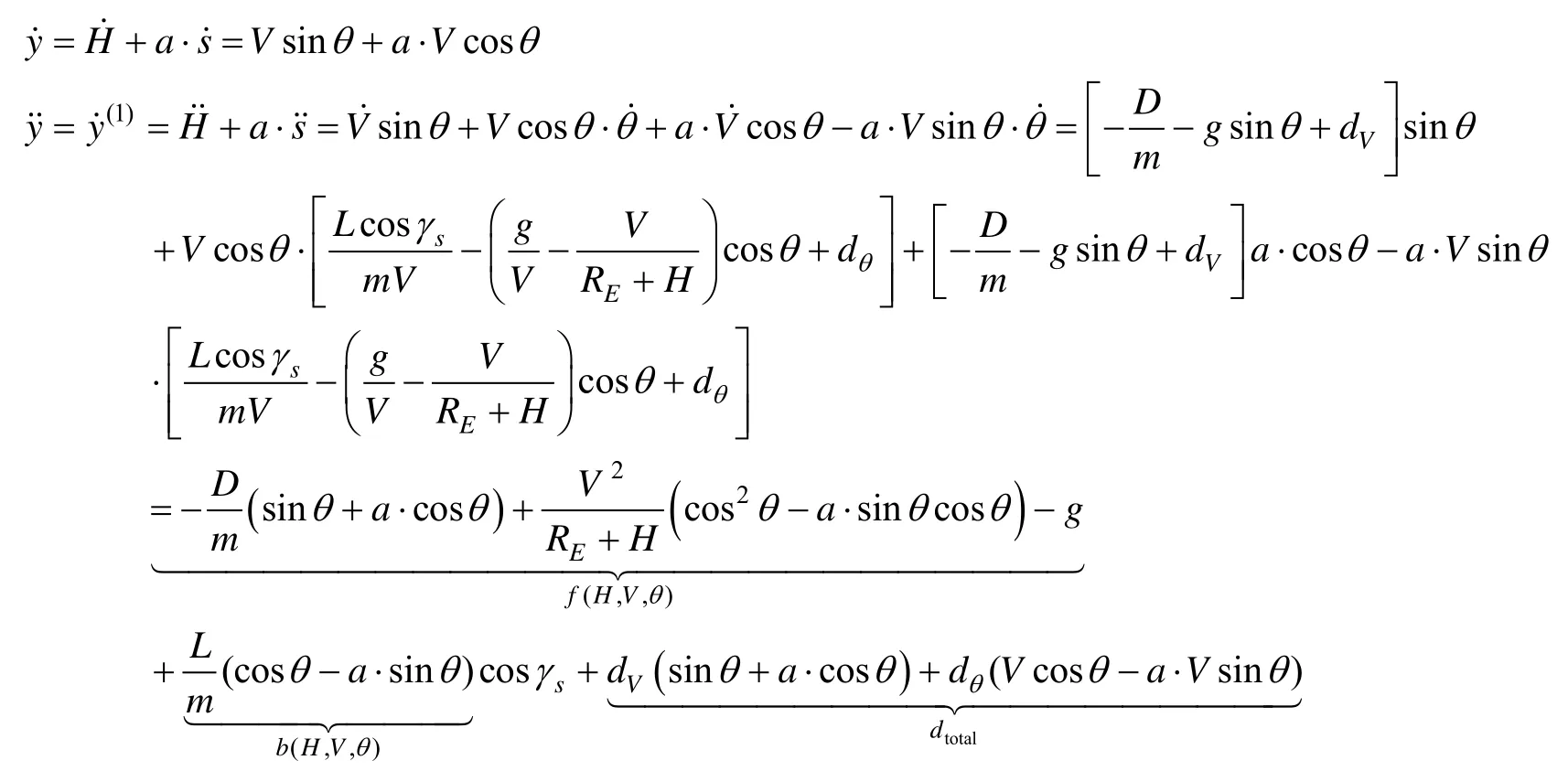
其中，f(H,V,θ)为描述输入输出线性化系统的标称动态系统项；b(H,V,θ)为标称控制增益项；dtotal为影响被控输出的总不确定性动态，其由速度通道和航迹倾角通道的总不确定项综合构成。不难发现，增广后的纵向运动学系统通过反馈线性化被转化为分别以cosγs和y为输入和输出的二阶积分串联型系统。特别地，当比例分配因子a= 0时，纵向平面制导任务退化为仅对高度的跟踪控制，该情况下难以保证再入速度的跟踪精度。因此，当a≠0时，通过调节分配因子可实现再入高度和速度误差的均衡控制。

若式（3）的不确定性动态dtotal可测或已知，则根据反馈线性化原理可设计如下的闭环控制律：

式(4)为不确定性动态dtotal可测情况的逆系统，因此系统的跟踪控制问题被转化为设计辅助输入v使得二阶积分串联系统具有较好的控制性能。由于实际工程中不确定性动态难以测量，因此该逆系统无法工程实现。另外，考虑自抗扰控制技术在补偿不确定性和抗扰控制方面的性能优势，特别是其核心组件扩张状态观测器在不需要获取系统不确定性先验知识的前提下实现总不确定性的实时精准观测，与基本控制器综合后可较好地弥补反馈线性化技术依赖于被控对象的精确模型导致鲁棒性不足的缺陷。因此，下面考虑结合扩张状态观测器技术对控制律(4)进行再设计。

不同于自抗扰控制思想[9-15]中将异于积分串联型的动态项视为总不确定项，这里由于标称动态系统项和控制增益已知，因此可将异于输入输出线性化系统标称模型的部分因素（即dtotal）视为总不确定项并扩展为系统的内部状态，记则增广后的纵向运动学系统可写为状态空间形式：

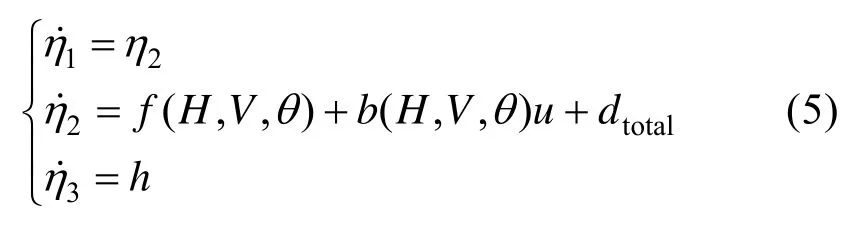
针对动态系统(5)可构造如下的模型辅助扩张状态观测器：

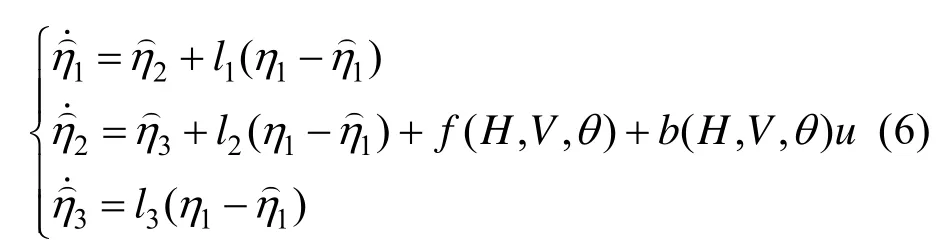
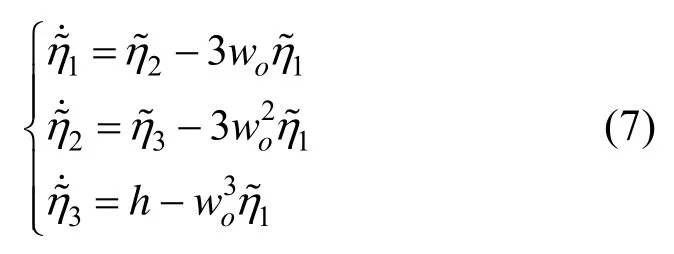
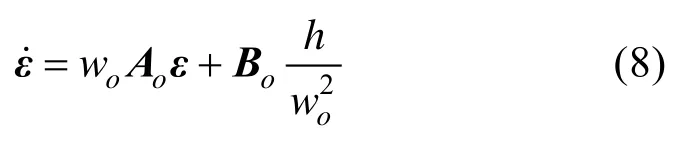
赫尔维茨矩阵。

定理1.若总不确定性动态导数有界并满足其中δ为正常数，则存在有界常数iσ及有限时间常数T1＞0，使当t≥T1＞ 0和wo＞ 0时观测误差并且对于适当的正整数k，观测误差最终收敛域和观测器带宽具有单调反比的关系并满足：

证明：直接求解观测误差动态系统(8)，其相应的解满足：

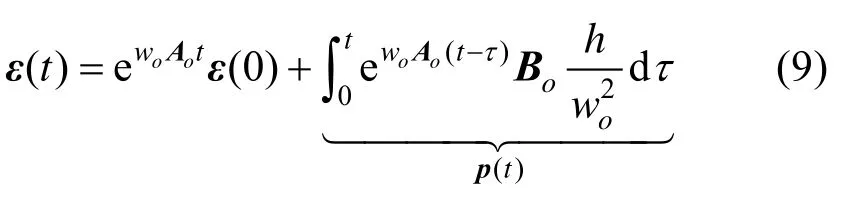
为得到pi(t)(i= 1,2,3)的估算上界，需要通过不等式缩放进一步确定的大小，对于系统(8)中定义的令得到：

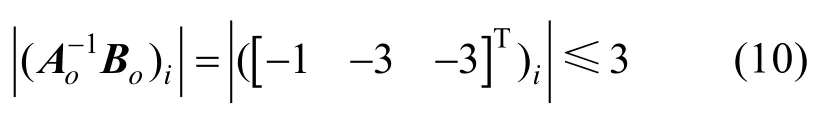
由于Ao为赫尔维茨矩阵，故存在有限时间常数T1＞0，使当t≥T1＞ 0时，有

基于式(10)和式(11)，令

可得

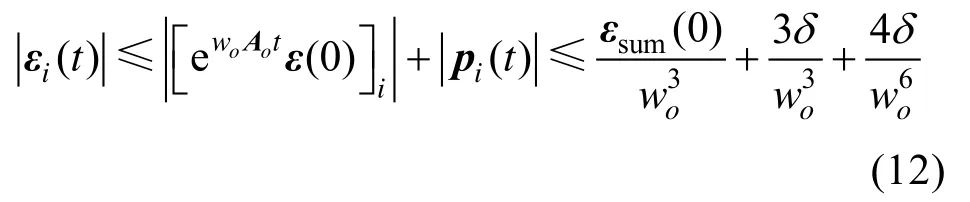
证毕。

由定理1关于模型辅助扩张状态观测器的收敛性证明可知，观测器的估计误差的最终收敛域与带宽成单调反比，与总不确定性动态的导数成正比。因此，可在系统带宽允许的范围内通过增大观测器带宽使观测误差快速收敛到零点附近的小邻域内。

定理2.假定总不确定性动态导数h关于iη满足全局利普希茨条件，对于增广后的纵向运动学系统(5)，结合模型辅助扩张状态观测器(6)所提供的观测值存在观测器带宽wo＞ 0和控制回路带宽wc＞ 0，设计的自抗扰再入制导律(13)使闭环系统的输出有界，并且跟踪误差渐近收敛。

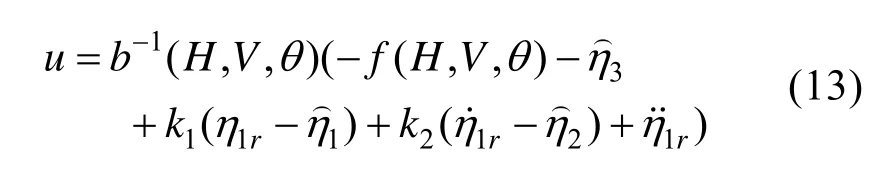
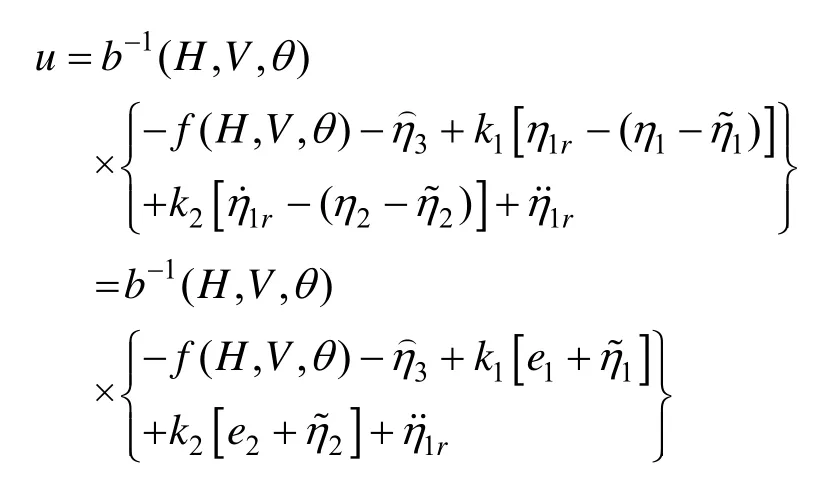
将闭环跟踪误差动态(14)进一步简写为如下矩阵形式：

为保证闭环跟踪误差动态渐近收敛，必须选择控制器增益k1,k2使特征多项式满足赫尔维茨条件。此外，为方便控制器调参，将该多项式的极点配置在-wc处，即由于观测误差最终一致有界，因此有同时借助文献[10]中对形如系统（其中N满足赫尔维茨条件，g(t)满足有界性假设）的稳定性证明可推断出：当总不确定性动态导数h关于ηi满足全局利普希茨条件，存在观测器带宽wo＞ 0和控制回路带宽wc＞0使证毕。

综上可知，在所设计的自抗扰再入制导律的作用下可保证再入高度和速度的加权误差渐近稳定。进一步，通过调节比例分配因子能在性能折衷的意义下实现高度和速度误差的均衡调控，以满足高超声速飞行器再入过程多约束和终端指标要求。

2.2 横侧向制导逻辑设计

借鉴航天器等再入飞行器横侧向几何制导逻辑的设计思路，即采用航向角偏差走廊进行控制，以实时调整倾侧角的符号引导再入飞行器横向运动不断逼近目标点，如图2所示。

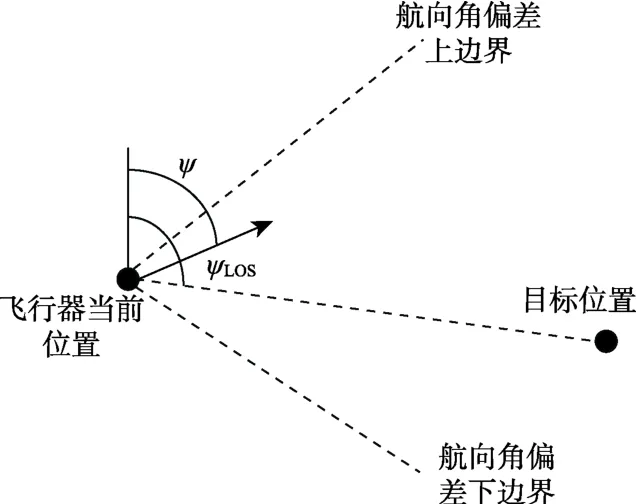
图2 横向制导相关参数示意图Fig.2 Schematic diagram of relevant parameters of transverse guidance

定义 ΔψH为航向角偏差门限值，设计为漏斗形的与速度相关的分段线性函数，即

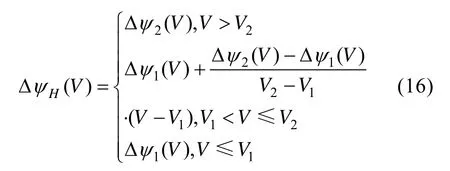
需要说明的是，ΔψH的选取原则是在尽量减少倾侧反转次数的前提下将飞行器引导至目标点，航向偏差走廊的相关设计参数Δψ2(V)和Δψ1(V)可由多次仿真实验确定最佳值。若当前再入飞行器的描述速度方向的航向角为ψ，定义航向角偏差为 Δψ=ψ-ψLOS，其中ψLOS表示飞行器当前点至目标点的视线方位角， 0 ≤ψLOS≤π，可由下式计算：

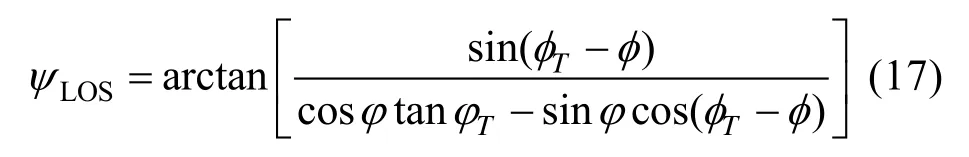
其中，φT和φT分别为目标点的经度和纬度。为确保航向角偏差始终位于所设计的航向角偏差走廊内，再入飞行器速度方向必须在初始时刻就瞄准终端目标点，则初始时刻的倾侧角符号可确定为

再入制导程序启动后，当飞行器的航向偏差角位于航向角偏差指定的区域内，则维持倾侧角符号与上一时刻一致；反之，若航向偏差角超出设定的走廊范围，则控制倾侧角符号反转，该制导逻辑的具体计算公式为

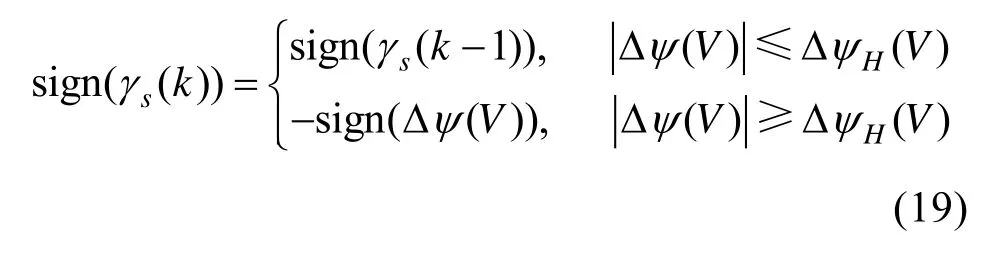
3 仿真验证

为验证所设计的自抗扰再入制导律对再入过程中存在气动参数组合拉偏情况下的适应性及对标准轨迹参数的跟踪能力，主要考虑以下两种仿真情况：

(1) 选取纵向制导律观测器带宽和控制器带宽分别为wo=20rad/s,wc= 5rad/s ，横侧向航向偏差走廊的设计参数为 Δψ2= 10°, Δψ1=5°,V2=3000m/s,V1= 500m/s ，制导系统的采样时间为0.05 s，为满足结构热防护和配平的需要，再入攻角剖面选择如下与速度相关的分段函数：

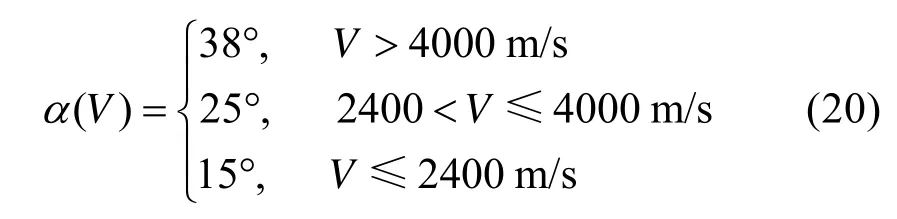
此外，于再入初始加入气动参数组合摄动：即升力系数和阻力系数误差均为标称值的20%，大气密度偏差为标称值的–10%，设置比例分配因子分别为a= 0.5,1，以考察其对自抗扰再入制导性能的影响；

(2) 再入制导律选取的控制参数和攻角程序剖面与情况(1)保持一致，令升力系数、阻力系数、大气密度偏差的分布类型服从高斯分布，偏差范围分别为标称值的±10%，±10%，±20%，并在上述组合摄动影响下进行蒙特卡罗实验，以充分验证自抗扰再入制导律对各参数偏差情况下的鲁棒性。

需要说明的是，在再入轨迹生成方面，由于高斯伪谱法是目前在航天再入制导和航空器轨迹优化领域应用较为广泛且求解效率较高的一种优化方法，并有大量的应用范例可供参考，故本文采用文献[16]所述的高斯伪谱法生成满足再入动压、热流密度和过载等硬约束和终端高度、速度、经纬度散布误差约束的三维再入轨迹以满足跟踪制导任务需求，具体步骤不再赘述。表1给出了上述仿真情况中再入制导任务的飞行参数和指标约束，其中：下标“0”和“f”分别表示初始和终端时刻；分别为再入任务所允许的最大热流密度、过载和动压，分别表示再入终端所允许的最大高度、速度、经纬度制导偏差。

表1 再入制导任务的飞行参数和指标约束Table 1 Flight parameters and index constraints of reentry guidance mission

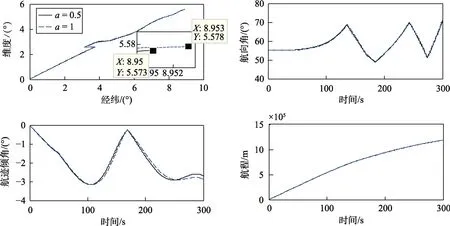
图4 再入制导相关状态变量的响应曲线Fig.4 Response curve of state variables related to reentry guidance

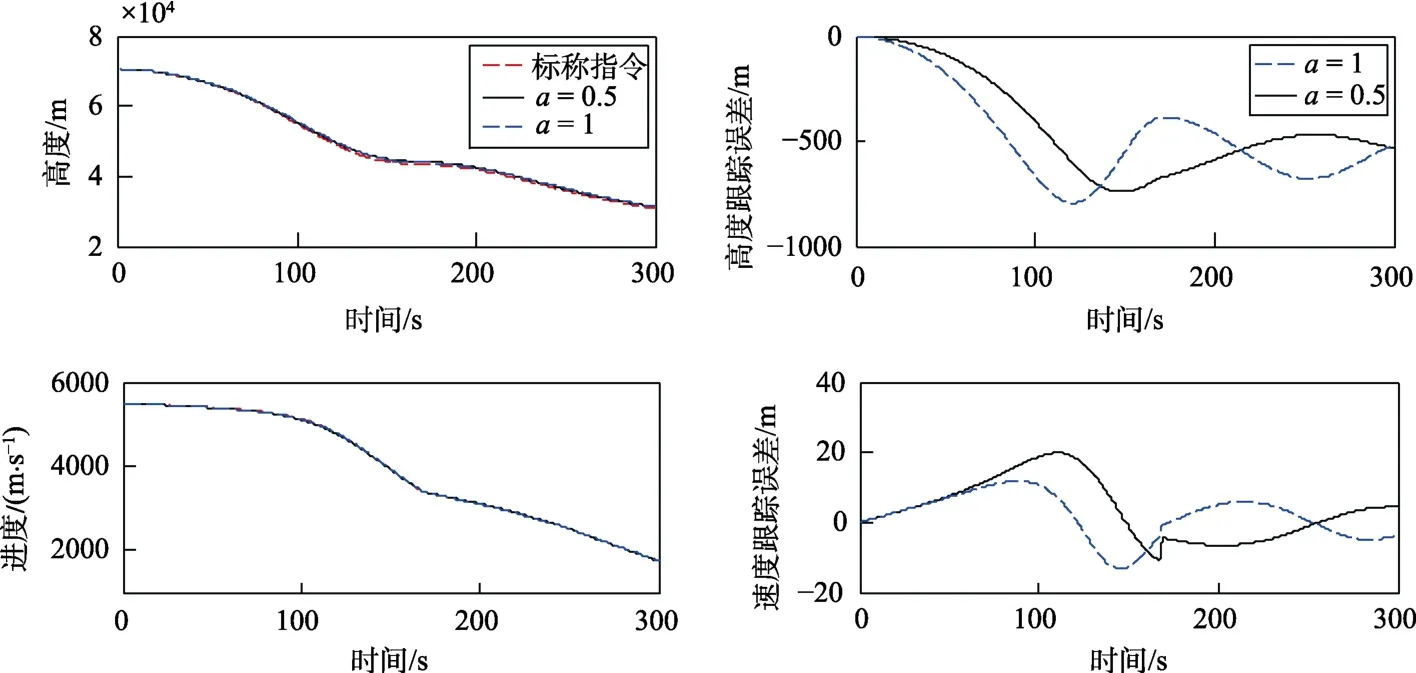
图5 再入高度和速度的跟踪响应曲线Fig.5 Response curve of reentry altitude and speed

图6 再入动压、过载及热流密度的响应曲线Fig.6 Response curves of reentry pressure, overload and heat flux density

图7 横向制导中航向角偏差和倾侧角变化曲线Fig.7 Variation curves of directional deviation and angle of bank during transverse guidance

图3～7分别给出了考虑气动参数扰动情况(1)时的制导效果仿真曲线。不难发现，由于自抗扰制导律中扩张状态观测器可实时对影响被控输出的总干扰动态进行精准估计（见图3），因此，在气动参数组合摄动及不同比例分配因子条件下均能提供满意的抗扰和制导性能，并较好兼顾了再入过程的安全性和再入终端制导精度。其中，高度和航程的加权误差均稳定维持在零点附近，再入动压、过载及热流密度等路径约束均满足既定要求，再入终端经纬度偏差均小于0.1°，终端高度和速度误差分别控制在1 km和20 m/s以内，航向角偏差始终位于设计的航向角偏差走廊内。值得提出的是，当比例分配因子提高时，意味着输出控制对航程的控制权重加大，导致再入速度全程的跟踪误差降低，但由于所设计的自抗扰制导律仅能在性能折衷的前提下实现高度和航程的联合控制，在速度控制性能提高的同时不可避免地引起高度跟踪方面的性能损失。因此，应根据具体的再入制导任务需求折衷选取比例分配因子实现高度和速度控制方面的均衡。另外，为实现纵向跟踪制导精度，倾侧角剖面再入全程幅值均较大（约为70°），为满足横侧向制导精度要求，倾侧角指令常伴随着航向角偏差超出既定走廊时进行2～3次的同步反转。可以预见，再入过程中倾侧角大幅度急剧滚转所引起的横侧向强耦合和强非线性效应将对姿态控制器的设计与综合提出严峻的挑战，也是后续研究需要重点突破的难点。

图3 自抗扰制导律再入跟踪误差及干扰估计曲线Fig.3 Reentry tracking error and interference estimation curve of ADRC

图8～10进一步给出了考虑气动参数组合摄动时的蒙特卡罗制导效果仿真曲线。蒙特卡罗仿真实验表明，在气动参数组合拉偏情况下的自抗扰再入制导律能满足预定的制导精度和路径约束要求，充分验证了所提出的自抗扰制导律具备较好的可行性和鲁棒性。

图8 再入制导相关状态变量的蒙特卡罗仿真曲线Fig.8 Monte Carlo simulation curve of reentry guidance related state variables

图9 再入动压、过载及热流密度的蒙特卡罗仿真曲线Fig.9 Monte Carlo simulation curves of reentry pressure, overload and heat flux density

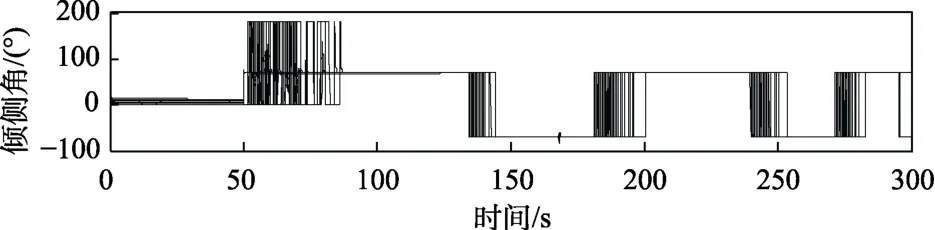
图10 倾侧角的蒙特卡罗变化曲线Fig.10 Monte Carlo variation curves of angle of bank

4 结 论

本文针对多约束条件及多种气动参数摄动影响的高超声速飞行器再入轨迹抗干扰跟踪问题，在标准轨迹制导方法的框架下，结合模型辅助线性自抗扰控制和基于航向角误差走廊的几何制导逻辑，提出了一种可满足制导任务需求的自抗扰再入制导律，通过蒙特卡罗仿真实验验证了该制导律的有效性。未来工作考虑将所提方法拓展至包含再入禁飞区和突发威胁的复杂制导环境，结合深度学习对非线性、高维函数的优异泛化能力，设计基于数据驱动与模型辅助的智能再入制导律，增强高超声速飞行器自主控制水平，提升面对多样化再入突防任务的适应性。