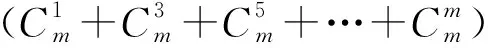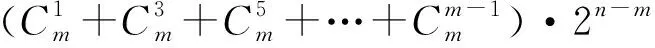2020年北京市高考适应性测试压轴题解析与推广

2021-07-15王芝平范方兵

数学通报 2021年5期

关键词：总和数组奇数

王芝平范方兵

(1.北京宏志中学 100013；2.北京市第二中学 100010)

(Ⅲ)对任意确定的一个数阵A0，证明：TS(A0)的所有可能取值的和不超过-4.

这是2020年3月北京市高考适应性测试数学卷最后一题，众多的字母符号、新颖的变换规则以及高度的抽象性，让相当一部分学生“望题兴叹”！为了让更多的学生更好地理解题意，我们在不改变题目本质的情况下，将试题重新表述如下：

若S={e1，e2，…，el}⊆U，其中，e1

(Ⅲ)对任意确定的一个数阵A0，证明：所有TS(A0)的和不超过-4.

下面给出我们对这道题的思考与解答过程.

谋定思路为了叙述方便，我们引入下面记号与术语：

1.将“数阵P经过φk变换得到的数阵Q”记作：φk(P)=Q，读作“数阵P经过k变换后得到数阵Q”.

2.将“φS(A0)”记作“φS(A0)=Al”，读作“数阵A0经过集合S变换后得到数阵Al”.显然A0经过集合S变换，就是A0依次经过集合S中各元素ei(i=1，2，…，l)对应的变换φei，最后得到Al.

前两问的目的既是帮助考生理解题意，也是给考生送一些分数，这在大型考试中是非常必要的.

对于第(Ⅲ)问，因为TS(A0)是A0经过集合S变换得到的数阵Al中四个数的和，所以一个值得考虑的问题是，数阵Al中每个数与原数阵A0中对应位置上的数有什么关系？

显然数阵Al中每个数与数阵A0中对应位置上的数要么相等，要么是一对相反数.“相等”与“相反”取决于集合S中的元素.

让我们再反复阅读题目中的这句话：

“对任意确定的一个数阵A0，证明：所有TS(A0)的和不超过-4.”

因为数阵A0是确定的，所以TS(A0)是随集合S变化而变化的.

所以，我们再来考虑集合S：由题设知，S是集合U的63个非空子集.经验告诉我们，从整体考虑问题可能更容易发现规律、更容易表述解题过程.所以我们不妨先设S是集合U的任意子集，则不同的集合S共有64个.当S=∅时，我们约定A0经过集合S——也就是∅——变换依然是A0，此时TS(A0)是集合A0中四个数的和.

这样所有的φS(A0)对应的数阵Al共有64个，对应的TS(A0)的值是64个整数，这64个整数的和我们称之为“总和”.

如果要知道每一个TS(A0)的值，这不仅是麻烦的，也是不必要的.

因为加法具有交换律，我们可以考虑所有数阵Al中第一行第一列的数，它们都是由A0中的数a11变换得到的，不是a11，就是-a11.直觉告诉我们a11和-a11的个数一样多，所以在“总和”中这64个数的和等于0.

同理，所有数阵Al中第一行第二列的数的和等于0；所有数阵Al中第二行第一列的数的和等于0；所有数阵Al中第二行第二列的数的和等于0.进而“总和”等于0.

再在“总和”中减去A0中四个数的和，即原题中所有TS(A0)的和等于-(a11+a12+a21+a22).因为a11，a12，a21，a22∈U，所以a11+a12+a21+a22≥4.所以-(a11+a12+a21+a22)≤-4，即所有TS(A0)的和不超过-4.

那么，从A0经过集合S变换得到Al，a11是保持符号不变，还是变成-a11？这既与集合S中是否含有a11有关，也与集合S中是否含有a12有关，所以对a11，a12是否相等进行讨论就是自然而然的思路了.

因为，在变换过程中，数阵中同一行的两个数的“变”与“不变”是同步进行的，所以我们可以整行考虑，先搞清楚一行中两个数的变化情况.

为了更清楚地把握问题的本质，又不失一般性，我们不妨从具体、简单的例子开始观察、思考.

设U={1，2，3}，数阵的第一行为数组A=(1，1)，U的所有子集共八个，分别为：

S0=∅，φ∅(A)=(1，1)，TS0(A)=2；

S1={1}，φS1(A)=(-1，-1)，

TS1(A)=-2；

S2={1，2}，φS2(A)=(-1，-1)，

TS2(A)=-2；

S3={1，3}，φS3(A)=(-1，-1)，

TS3(A)=-2；

S4={1，2，3}，φS4(A)=(-1，-1)，

TS4(A)=-2；

S5={2}，φS5(A)=(1，1)，TS5(A)=2；

S6={3}，φS6(A)=(1，1)，TS6(A)=2；

S7={2，3}，φS7(A)=(1，1)，TS7(A)=2；

所有TS(A)的和等于0.

因为U={1，2，3，4，5，6}的所有子集中，含有1的子集共有25=32个，在这32个子集的变换下，(1，1)变成了(-1，-1)；U的其余32个子集中都不含1，在这32个子集的变换下，(1，1)仍然为(1，1).

所以在U所有子集变换下，(1，1)的64个“象”中，有32个(-1，-1)，32个(1，1)，显然，其总和为0.

设一个数阵的第一行为二元数组(1，2)，对于U的含1不含2的子集，如{1，3，4}，数组(1，2)在该集合的变换下得到(-1，-2)；对于U的含2不含1的子集，如{2，3，4}，数组(1，2)在该集合的变换下得到(-1，-2)；对于U的既含1，又含2的子集，如{1，2，3，4}，数组(1，2)在该集合变换下得到(1，2)；对于U的既不含1又不含2的子集，如{3，4}，数组(1，2)在该集合的变换下仍然是(1，2).

这样就必须得清楚，对于数组(a11，a12)而言，U的所有子集中含a11而不含a12的集合有多少个，含a12而不含a11的集合又有多少个，既含有a11，又含有a12的子集有多少个，既不含a11，又不含a12的子集又有多少个.只要这些问题搞清楚了，问题就迎刃而解了.

规范解答(1)若a11=a12，在集合U的所有子集中含a11的集合有25=32个，所以A0经过这32个集合变换后得到的32个数阵中，第一行的两个数分别变成了-a11，-a12；而不含a11的集合也有25=32个，A0经过这32集合个变换后得到的32个数阵中，第一行的两个数依然分别是a11，a12.

此时，所有数阵(Al)中第一行的两个数的和的和等于 32(-a11-a12)+32(a11+a12)=0.

(2)若a11≠a12，则集合U的所有子集中含a11而不含a12的集合有24=16个，A0经过这16个集合变换后得到的16个数阵中，第一行的两个数分别变成了-a11，-a12；含a12而不含a11的集合也有24=16个，同理又有16个数阵中第一行的两个数分别变成了-a11，-a12；

集合U的既含有a11，又含有a12的子集有24=16个，A0经过这16个集合变换后得到的16个数阵中，第一行的两个数依然是a11，a12；集合U的既不含a11，又不含a12的子集也有24=16个，A0经过这16个集合变换后得到的16个数阵中，第一行的两个数依然是a11，a12.

此时，所有数阵Al中，第一行的两个数的和的和等于(16+16)(-a11-a12)+(16+16)(a11+a12)=0.

总之，所有数阵Al中第一行的两个数的和的和等于0.

同理，所有数阵Al中第二行的两个数的和的和等于0.

所以，64个数阵Al的四个数的和的和等于0.

所以，当S是集合U的所有非空子集时，所有TS(A0)的和等于-(a11+a12+a21+a22).

因为a11，a12，a21，a22∈U，

所以a11+a12+a21+a22≥4.

所以-(a11+a12+a21+a22)≤-4，

即所有TS(A0)的和不超过-4.

反思启迪数学之难学，往往在于数学符号的抽象.许多同学看见陌生的符号就头疼.用数学符号表示某些数学对象是数学研究和数学解题的常用手段，也是重要的数学思想和能力.理解并掌握符号表达能力的核心是对新定义的数学符号的理解和运用.符号表示不仅是用字母表示数字，还包含数学中的一切公式、特殊约定的字符以及新定义的符号等.

第三问——求所有TS(A0)的和，初看上去好像杂乱无序，无从下手，冷静思考后我们发现，从全局出发，利用加法的交换律，可以改变运算顺序，变“局部求和”为“整体求和”.理解到这一点后，我们就不会纠缠于问题的细枝末节，而是注重通览全局，通过分析问题的整体结构特征，进行整体转化，达到问题解决的目的.

建议同学们摒弃“重结果轻过程”式的学习，回归教科书，关注知识的形成过程并感悟其中蕴含的数学思想方法，夯实基本技能，追求对数学知识的本质性理解，提升数学素养.在解题训练中，必须跳出题海、远离各种技巧，注重通性通法，养成用数学概念思考问题、解决问题的好习惯.遇到新颖、陌生的含有“新定义”的题目时，要重视审题环节，反复认真研读题目，适当时候变换三种数学语言(自然语言、符号语言、图形语言)来对问题进行重新表述，使得对问题的刻画是全方位、多角度的，有利于理解题目所定义的新概念、新规则、新运算，在此基础之上，还要善于从特殊的、简单的、极端的情形入手去“写写看”，通过对这些特殊情形的探讨，获得一些结论，受到一些启发，从而找到解决问题的有效途径.

变式研究

1.对于本题，如果求TS(A0)的所有可能取值的和，那么结果等于什么呢？