课堂教学中的困惑与对策

张跃红

(南京师范大学附属中学 210003)

一线教师每天都与课堂教学打交道，难免会遇到各种各样的困惑.在这些困惑中，有些是共性的，也有些是个性的.针对困惑，教师也有着各自不同的处理办法.本文结合笔者的教学实践，针对在课堂教学中通常会出现的困惑，谈一些想法及做法与同行交流.

1 有关探究的困惑与对策

众所周知，数学探究是高中数学课程中引入的一种新的学习方式，它有助于学生初步了解数学概念和结论产生的过程，初步尝试数学研究的过程，有助于发展学生的创新意识和实践能力.

但是要不要探究？如何探究？一直是困扰着一线教师的问题.因为有些教师在课堂教学中，实施的探究活动并未达到良好的教学效果，不但浪费了大量的教学时间，影响了教学进度，同时也让学生失去了参与的兴趣，挫伤了教师的积极性，探究活动则变成了“鸡肋”，食之无味，弃之可惜.

真正的探究活动要“探”在能力的获得上.教师首先要想清楚，通过探究活动要培养学生哪些方面的能力.同时，也要考虑学生自身能力、教学内容、教学时间等方面因素的影响.首先，探究教学需要学生具备相当的知识储备和较高的思维水平，因为只有达到了一定的水平，才能真正探究起来，否则就是被教师“牵着鼻子走”进行假探究”；其次，探究式教学内容不宜过深和过浅，否则都会变成“假探究”.内容过浅，没有探究的必要；过深，学生听教师讲解尚且困难，自己探究更会困难重重；最后，由于探究式教学往往费时很多，就要选择合适的时机，同时也可以适当地调整教学形式；如果课堂时间有限，可以把学生分成小组，利用课余时间进行探究活动，课内进行展示.

鉴于此，可以把“正弦定理”一课设计成“研究三角形边角关系”的单元教学课.

本节课采用探究式教学方法.教师将学生分成若干小组，利用课余时间进行探究.课堂上采用小组汇报的形式，交流展示他们的研究成果.

整节课分成以下4个环节.

环节1 小组汇报 展示成果

学生通过探究发现三角形的边角关系中，存在三个定理，分别是：

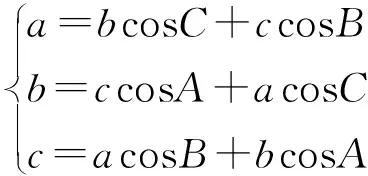
参与汇报的小组，主要呈现出三种得到这些定理的方法，分别是：

(1)将一般三角形化为特殊三角形(化斜为直)，通过直角三角形的边角关系得到三个定理；

(2)借助向量进行研究，通过将向量等式数量化的方法(即将向量等式平方，或者利用数量积运算)得到定理内容；

(3)借助坐标系进行研究，通过建立平面直角坐标系，利用等面积法，或者距离公式得到定理内容.

环节2 回顾过程 反思方法

教师请同学们回顾，是如何想到利用构造直角三角形、向量和坐标系的方法来研究三角形边角关系的？

设计意图是挖掘各种研究方法背后隐藏的“金子”，使研究方法系统化，进而形成学生自己的研究能力.

各个小组的代表分别谈了他们的想法：(1)“化斜为直”是“一般”到“特殊”思想方法的体现；(2)向量具有“代数”与“几何”特征，是解决三角形问题的有利工具；(3)坐标系是将“几何问题”转化为“代数问题”的有效途径.同时，每个小组又对不同研究方法进行了比较、分析，指出各种方法的利弊以及需要注意的问题.

环节3 观察定理 思考用途

教师引导学生观察这三个定理的结构特征及用途，并归纳总结出应如何观察等式特征，从哪些角度进行观察；如何使用这三个定理解决问题，以及使用时需要注意的问题，教给学生方法.

环节4 领悟联系 拓展延伸

教师引导学生再研究：

(1)每个定理都有三个等式，等式之间是否可以相互转化？

(2)三个定理之间是否存在某种联系？

学生们经过讨论研究发现，每个定理的三个等式可以相互转化，知道其中两个就可以得到第三个.三个定理间存在联系，三个定理之间可以相互证明，即用正弦定理可证明余弦定理，用余弦定理可证明射影定理，等等.

2 有关概念教学的困惑与对策

概念是思维的细胞，理解概念是所有数学活动的基础，只有在概念清晰的条件下，才能进一步开展其他的数学活动，概念课的重要性是不言而喻的.

“函数的单调性”是函数概念的下位概念，它比函数的概念容易理解，但很重要，在数学中具有核心地位.有教师这样设计这节课：上课伊始，教师给出几个函数的图象，让学生观察图象的特征，然后给出函数单调性的定义.之后，教师对定义中的关键词“任意的”进行特别强调，提醒学生注意，接下来进行巩固练习.

但令人困惑的是，教师自认为已经讲得明明白白，学生也把概念背得滚瓜烂熟，但在练习时要么错误百出，要么没有解题思路，无从下手.经过教师讲解，学生似乎又“明白了”，一旦自己独立完成，问题又来了.为什么学生明明知道函数单调性的定义，却不能利用它来解决问题呢？

究其原因，学生没有理解概念的本质.因为概念是教师“抛给”学生的，不是通过自己的理解建立起来的.众所周知，概念越是基本，其应用范围就越广，学生通过对这些概念的学习，所感悟到的数学就越本质.由此而养成的思维习惯及思维方式，将会对学生的终身发展产生根本性的影响.但往往越是基本的概念越容易被教师“一笔带过”，因为教师认为概念是“规定”好的，直接告诉学生就行了，没有什么好讲的.但事实上，概念越是基本，往往对它们的理解和掌握也越难，需要的时间也越长.“纸上得来终觉浅，绝知此事要躬行”，为了表面上的“实惠”，舍弃概念教学的完整过程，直接将概念“抛给”学生，把节省出来的时间用于大量的训练，以期望达到快速掌握的教学效果，这种做法只能是事与愿违.

如何设计概念课的教学？不妨以“函数的单调性”一课为例.

本课分为以下5个环节.

环节1 设置情境 引出课题

教师引导学生思考：在研究了函数的概念、图象和表示方法之后，还有哪些方面的内容需要去研究？

函数是描述事物变化规律的数学模型，函数的变化规律显然值得研究.通过设置现实生活中的例子(比如心电图，股市走势图等等)，让学生感受函数变化规律的意义，明确研究的内容和方法.

环节2 观察图象 得到直观定义

教师给出一些函数的图象(可以是学生熟知的一次函数、二次函数的图象，也可以是不熟知的函数图象)，请学生观察这些函数图象有哪些变化规律.意图引导学生从形的角度，得到单调函数的直观定义：

设函数的定义域为A，区间I⊆A.在区间I上，若函数的图象(从左至右看)总是上升的，则称函数在I上是增函数；在区间I上，若函数的图象(从左至右看)总是下降的，则称函数在I上是减函数.

环节3 探幽入微 得到描述性定义

凭借函数图象观察出的性质，仅得到了定性刻画，只能说是对函数的变化情况有个大概了解，以此作为定义，显然是不够的，需要量化.如何进行量化？那就需要把函数图象的形迁移到数.

教师可以借助几何画板作出一些函数的图象，测量出其图象上点的横纵坐标，把它们制成表格，实现从形到数的转化.通过观察表格中自变量的值与对应的函数值的变化规律，引导学生把从形中看到的单调性(即图象语言)，过渡到用自然语言来表述，进而得到函数单调性的描述性定义：

设函数的定义域为A，区间I⊆A.在区间I上，若随着自变量x增大，函数值y也增大，则称函数在区间I上是增函数；在区间I上，若随着自变量x增大，函数值y却减小，则称函数在区间I上是减函数.

环节4 设置问题串 得到形式化定义

虽然得到了函数单调性的描述性定义，但它还不是量化的，要把定性的数量变化关系转化为定量的数量变化关系.这是本课的重点，也是难点.

教师可以设置问题串：

问题1对于区间(a，b)上任意的x都有f(x)>f(a)，能否说明f(x)在此区间上单调递增？说说理由.

问题2对于给定区间上存在无数个自变量x，当自变量变大时，相应的函数值也变大，能说明函数在此区间上是单调递增的吗？说说理由.

问题3函数y=x在R上单调递增的，能否用数学符号表示？

通过问题串进行一步步的引导，让学生思考、体会，最终“水到渠成”地得到函数单调性的形式化定义：

设函数的定义域为A，区间I⊆A.如果对于区间I内的任意两个值x1，x2，当x1f(x2)，则称函数在区间I上是减函数.

环节5 回顾过程 总结方法

通过练习、小结等活动，让学生回顾研究过程，即“图形直观——定性刻画——定量刻画”，总结研究方法，并将所获得的研究方法用于其他知识中去.

从以上教学设计可以看出，概念教学的基本环节是：①设置现实情境，让学生感受研究的价值和意义；②给出具体的例证，并对它们的属性进行分析、比较；③抽象概括出所给例证的共同本质特征，进而得到概念的本质属性；④用准确的数学语言给概念下定义；⑤运用实例从正、反两个方面，对概念进行辨析；⑥思考概念的用途及与其他相关概念的联系，学以致用.

值得注意的是，概念教学特别需要有耐心，需要循序渐进的渗透和提高，需要学生亲身经历从具体到抽象的概括过程，不可急于求成.

3 有关解题套路的困惑与对策

要不要教给学生解题套路，也是经常困扰一线教师的问题.因为解题套路确实让学生和教师都尝到了“甜头”.对于学生而言，不需要动脑筋，只要背下来，照搬就是了；对于教师而言，也不需要动脑筋专研如何备课了，只要归纳整理好各种题型的解决办法，然后照本宣科告诉学生，就万事大吉了.

如果总是教给学生解题套路，结果会如何呢？势必导致学生只会做“熟题”，不会做“生题”.

因为套路是针对某一类问题给出的固定解法，它不会变，是僵化的.一旦问题改变，其解决方法就立刻无法使用.

比如，问题1：当x∈R时，关于x的不等式kx2+kx+1>0恒成立，求实数k的取值范围.

如果问题1的教学设计如下：

第一步，首先考虑当k=0时，1>0满足条件；

第二步，当k≠0时，欲使当x∈R时不等式恒成立，只需开口方向向上(k>0)，并且判别式Δ=k2-4k<0即可，解得0

第三步，综上所述，实数k的取值范围是0≤k<4.

这样的教学就是“解题套路”，因为它只告诉学生怎么做，却不告诉学生为什么这样做.

首先，为什么要考虑“k=0”的情况？其次，明明是不等式问题，怎么就联系到了二次函数的图象？这些问题不解决，学生无法理解其解法，只能是记下来然后照搬，一旦题目改变，就束手无策了.

要让学生从根本上理解解决问题的方法，就需要教师讲清楚原理，即解决问题的思想和方法.解决问题1的根本，就是函数与方程思想.函数、方程和不等式，好比是一家人中的“三兄弟”，“老大”函数是最有能力的，因为它比其他两个“兄弟”多了一样工具——图象(这又联系到了数学的另一个思想方法，即数形结合).当其他两兄弟遇到困难时，“老大”函数就要出手帮助.问题1属于不等式问题，但它遇到了困难，凭借自己的本事它解决不了(不等式本身能解决的问题，仅限于求解)，势必要寻求 “老大”函数的帮助，这样就需要将不等式转化为函数.

如何转化呢？令y1=kx2+kx+1，y2=0，原不等式kx2+kx+1>0转化为y1>y2，问题1即转化为：当x∈R时，函数y1的图象恒在y2(即x轴)的上方，求实数k的取值范围.

对于函数y1=kx2+kx+1，当然要考虑k是否为0的情况，否则我们无法判定函数的类型，也就无法画出它的图象.当k=0时，y1=1为常函数，显然在x轴上方；当k≠0时，函数y1为二次函数，其图象欲恒在x轴上方，势必要开口向上(k>0)且与x轴无交点(Δ<0).

当然，将不等式转化为函数时，不一定非要令y1=kx2+kx+1，y2=0，只要以不等号为界，左边一个函数，右边一个函数即可.至于谁在左边，谁在右边，完全取决于题目的结构特征.

思想和方法是解决数学问题的灵魂，起到高屋建瓴的作用.无论题目千变万化，领悟了思想和方法就能以不变应万变.比如问题1，可变为：

关于x的不等式kx2+kx+1>0，当分别满足下述条件时，求实数k的取值范围.

(1)当x∈R时，不等式能成立；

(2)当x∈[1, 2]时，不等式恒成立；

(3)当x∈[1, 2]时，不等式能成立.

通过这样的教学，解决的就不单单是一个问题1.或许某些问题的解决，确实需要教给学生一些套路，但如果全部是套路，试想，那得需要多少套路才能应对各种变化问题？反言之，学生一旦掌握了思想和方法，学会了思考和分析，建立起自己的思考体系，在面对各种纷繁复杂的新问题时，就会从容不迫，得心应手地去应对.

4 有关书写规范的困惑与对策

近些年，由于在高考阅卷中，评分标准比较严格，教师担心学生由于书写不规范而白白失掉一些分数，在课堂教学中强调书写规范的氛围悄然兴起.有些教师把“书写规范”视为课堂教学最重要的任务，从而冲淡了重要知识、内容的讲解；有些教师把握不了书写标准，索性“眉毛胡子一把抓”，就要求学生写得越多越好；有些教师矫枉过正，甚至出现了学生作业中写的“设点P”，教师要求改成“不妨设点P”，并且让学生重新书写一遍的极端情况，等等.

强调书写规范的目的，是为了让学生有逻辑地回答问题，培养学生思维的严谨性.何为有逻辑地回答问题？就是要讲清楚每一步骤的因果关系.没有“因为”的存在，只给出最后的“结果”，显然是不符合逻辑的.

所以，我们在课堂教学中，强调书写规范固然重要，但更重要的是讲清楚书写规范背后的原因.哪些步骤该写，哪些可以不写，其中的原因是什么，一定要让学生心里清清楚楚、明明白白.否则，学生只能是畏手畏脚，既害怕写多了浪费时间，又害怕写少了被扣分，患得患失、稀里糊涂，反倒严重影响了正常的答题节奏和心情.

针对书写规范，不妨让学生在作答时，想清楚以下几个方面的问题：

(1)书写的每一个逻辑段，是否能保证因果关系齐全，即有“因”有“果”；

(2)漏写这一步，是否会出现科学性错误；

(3)使用了题目中没有出现的条件，是否交待清楚了；

(4)在使用已知定理、公式、结论时，是否有特别需要说明的地方.

教师可以结合教学实际情况，对学生出现的书写问题进行有针对性的指导.不妨尝试一下以下做法：(1)把习题课分成“思想方法课”和“书写规范课”.“思想方法课”目的是，教会学生如何思考、分析问题，选择科学合理的解题思路，进而解决问题；“书写规范课”目的是，教会学生如何会书写，保证解题过程条理清晰，有理有据.把习题课分成这样两类后，教学侧重点突出，目的明确，针对性会更强；(2)以学生的书写过程作为实例进行评价，“正例”与“反例”都要选择，师生共同评价.评价时要指出“正例”好在哪里，“反例”坏在哪里以及如何修正；(3)若教学时间允许，教师可以板书一道题目完整的解题过程，让学生亲眼看见，感受也会更加深刻；(4)书写规范是一种习惯，在平时就要养成.对学生平时作业与大型考试的书写要一视同仁，不能区别对待、厚此薄彼.习惯一旦养成，规范书写就不是一件要刻意完成的任务.