基于最大熵谱估计的高能电子周期特性研究*

万美言，鲁同所,2，廖偲含，于白雪，高贝贝

(1. 西藏大学理学院，西藏 拉萨 850000；2. 中国科学院上海应用物理研究所，上海 201800)

高能带电粒子组成的空间辐射环境是影响航天器在轨飞行安全最重要的空间环境之一， 主要包含：(1)高能带电粒子入射物质中，在航天材料表面或内部发生充放电反应，导致航天器材料内部因电磁干扰而发生故障；(2)高能电子形成电流脉冲，改变元器件内部的电荷分布，造成元器件的逻辑状态混乱而引发故障甚至失效；(3)高能带电粒子的辐射效应通过电离作用导致航天器的材料、元器件性能变差，直至失效，同时辐射效应也会对人体造成损伤，严重影响航天员的安全[1]。

风云二号是我国研制的第1代地球同步轨道气象卫星，与极地轨道气象卫星相辅相成， 构成我国气象卫星应用体系[2]。风云二号D星于2006年12月8日成功发射升空，在高度为35 783～35 788 km的高轨道上飞行，包含高能质子、电子、氦离子等共7个能道。风云二号D星定位于东经86.5°赤道上空，轨道周期为1 436.04 min，轨道倾角为1.84°，自旋稳定，转速100 r/min。风云二号D星搭载的空间粒子探测器是空间环境监测器的一部分，与之前发射的A星共同实现双星观测，发挥1 + 1大于2的系统效益，提高卫星观测频次，扩大卫星的观测范围，实现立体观测和动态监测[3]，为研究高能粒子的周期特性提供更精确可靠的数据，同时也为研究太阳活动和地磁活动对空间环境的影响提供参考。

本文主要利用最大熵谱法研究近地空间高能电子(≥2.0 MeV电子通量)的周期变化特征，同时对比与Levinson-Durbin和Burg算法[4]的优缺点。研究采用的数据覆盖时间范围为2006年12月19日至2012年5月21日，时间精度为5 min，对数据空缺部分均进行插值处理。

1 研究方法

1.1 最大熵谱法

傅里叶变换是常用的时变分析方法[5]，而本文采用最大熵谱法，其原因一是傅里叶变化是一种整体变化，在研究周期特性上缺乏时间和频率的定位功能，不能反应某个时间段的信号发生的变化，也无法获得某一频率出现的时刻信息；其二，傅里叶变化对非平稳信号存在局限性。本文研究的高能电子通量的频率是随时间变化的，用傅里叶变换进行分析只能给出高能电子通量频率变化的整体效果，不能完整地反映某一时刻信号的本质特性。

最大熵谱法具有髙分辨率和短时性的特点，原理可概述为利用已有的自相关函数值，以最大熵为前提，利用N个已知的自相关函数值外推其他未知的自相关函数值，最后作频域变换，求得连续的功率谱估计，为研究数据的周期特性提供了算法支撑。具体步骤为[6]

(1)计算初始值

(1)

(2)求预测均方误差pm递推公式

(2)

(3)求解自相关模型的反射系数km

(3)

(4)求前向预测误差和后向预测误差，然后顺次估计反射系数km

(4)

(5)由Levinson递推，求出阶次m=2时自相关模型参数

am(i)=am-1(i)+kmam-1(m-1)i=1,2,…,m-1 ，

am(m)=km.

(5)

重复上述过程，直到m等于所需自相关模型阶数，求出所有的自相关模型参数，然后预测时间序列的最大熵，即

(6)

其中，k(k=1, 2, …,p)为p阶线性预测滤波器系数；σ2为预测滤波器的误差功率。

1.2 Levinson-Durbin和Burg 算法

Levinson-Durbin和Burg算法都是线性预测方法，是根据已知的时间信号序列计算功率谱估计值的递推算法。Burg算法利用前向滤波误差fn,t和后向滤波误差bn,t求出滤波误差功率为最小的anm，再根据Levinson-Durbin算法计算自相关模型参数ani。要利用自相关模型进行功率谱估计，需要用到Yule-Walker方程：

am(i)=am-1(i)+kmam-1(m-i),i=1,2,...,m-1.

(7)

M阶自相关模型的第m+ 1个参数G满足

G2=pm，

(8)

pm是预测功率误差，可得递推公式

pm=pm-1(1-km2).

(9)

由(9)式进行递推，可求得最终表征随机信号的自相关模型的p+ 参数，最后求得随机信号的功率谱密度为

(10)

1.3 自相关模型阶数的确定

自相关模型阶数的确定十分重要，在最大熵谱法和Levinson-Durbin，Burg算法中都会用到。若选择太小的阶数，得到的功率谱图太平滑，不能有效地分辨时间序列周期分量；若选择太大的阶数，会影响最大熵估计值的稳定性。自相关模型的最佳阶数需要在递推过程中确定。使用Levinson递推算法，由低阶到高阶的每一组参数及模型的最小预测误差功率pmin是递减的。理论上，当p值达到期望值，或不再发生任何变化时，即满足最佳适用性，此时的阶数就是应选的最佳参数。以下是两个常用的阶数适用性检验准则[7]。

1.3.1 最终预报误差准则

最终预报误差准则考虑预测值和真实值之间的误差，以误差最小为原则，而使误差最小只对应一个阶数值r。由此FPE(r)定义为

(11)

其中，N为高能电子通量的数据样本数。

1.3.2 赤池信息准则

赤池信息准则是建立在熵的概念上，可以判断所估计模型的复杂度和模型拟合数据的优良性，定义AIC(r)为

AIC(r)=2r-2ln(L)r.

(12)

阶数r取值发生变化，FPE(r)和AIC(r)的值也发生变化。在r取某值时，FPE(r)和AIC(r)的值都为最小值，那么此时所取的r就是最佳阶数。

在实际运算中发现，数据较短时，所得的最佳阶次偏低，且以上两个准则所得的最佳阶数基本一致，即

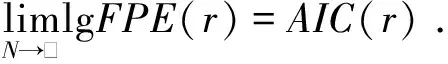
(13)

2 高能电子通量的周期特性

2.1 数据选取

本文选择分析能道≥2.0 MeV的高能电子通量是能量极高的带电粒子。由于初始数据在2009年12月6日～12月30日、2011年2月2日～2月11日、2011年8月22日～8月24日等时间段缺失，为了避免缺失数据对研究周期特性的影响，利用函数Fillmissing通过MATLAB实现对所收集数据进行插值处理，图1是2006年12月19日到2012年5月21日高能电子在能道≥2.0 MeV的电子通量变化情况，数据频次为5 min，每日24 h，平均每日288个数据，经过插值处理后，数据量超过50万个。

2.2 数据处理

高能电子通量在2006年12月19日～2012年5月21日的变化情况见图1，由图1可知，由于时间跨度长，数据量庞大且数据密集，电子通量曲线高低不平，直接用于分析研究很难直观地给出周期特征，故做日平均处理，如图2为高能电子在2006年12月19日到2012年5月21日的日平均通量。由于数据庞大，我们只选择研究以天为量级的电子通量周期且日平均数据将平滑掉短周期时变特性，故采用日平均数据是合理的。图2显示高能电子通量存在一定的周期，且周期不唯一，有主周期和次周期，根据图像的分布特点，可以看出在2006年12月19日～2008 年12月19日和2009年12月19日～2012年5月21日的曲线波动较大，而在2008年12月19日～2009年12月19日的通量变化十分微小。为了更好地研究2006～2012年高能电子通量的周期特性，我们采用最大熵谱法[8]。

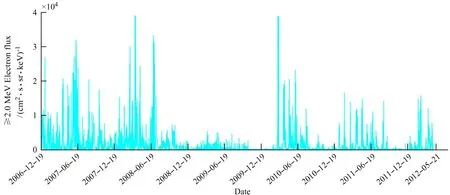
图1 高能电子通量在2006年12月19日～2012年5月21日的变化情况Fig.1 Changes in high-energy electron flux between December 19, 2006 and May 21, 2012

由于风云二号D星的粒子探测器探测的高能电子通量数据存在部分缺失，为了便于处理，我们对原始数据进行插值，然后采用归一化方法(图3)，减少插值数据对原始数据的影响以及对整个研究结果的干扰[9]。由图3可知，数据分布特点与图2几乎一致，表明使用插值后的数据研究周期特性较为合理。

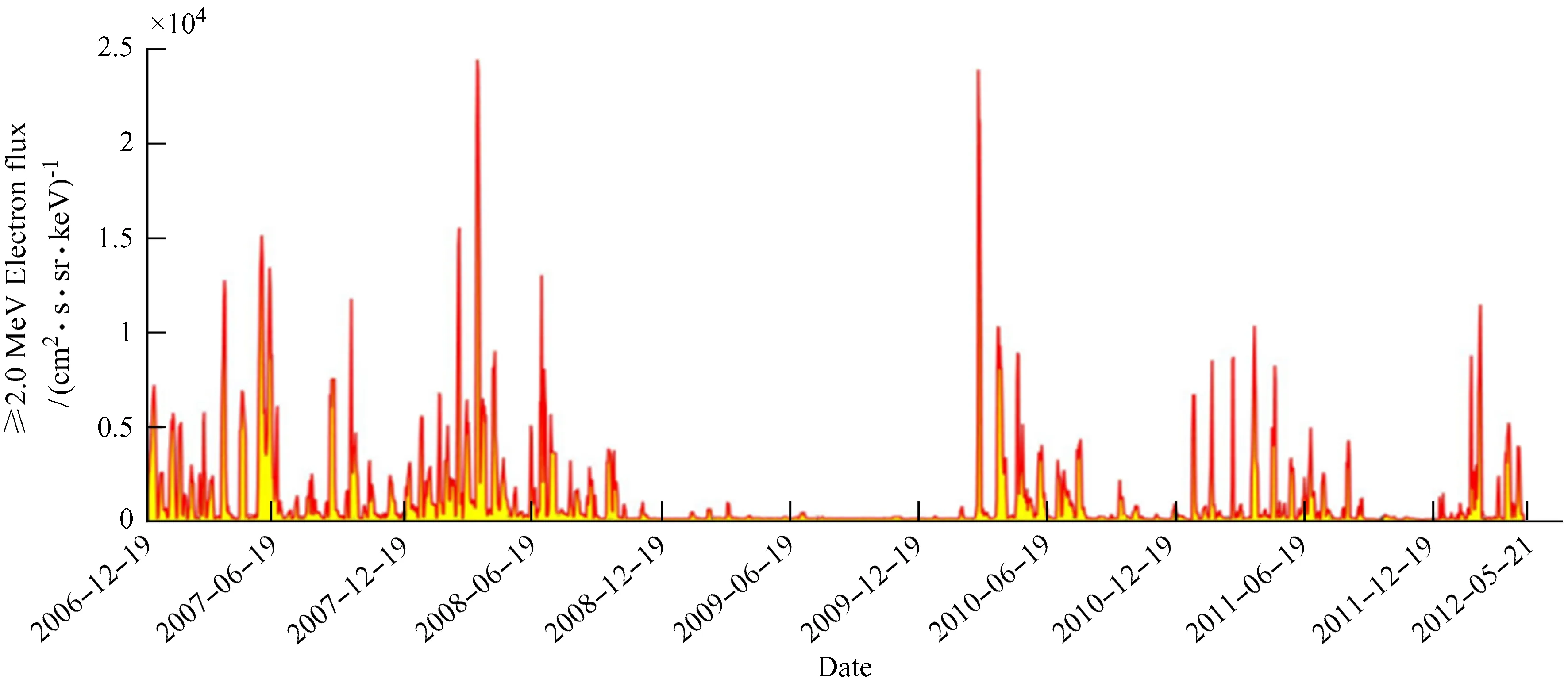
图2 高能电子在2006 年12月19 日～2012年5月21日的日平均通量Fig.2 The daily average flux of high energy electronics between December 19, 2006 and May 21, 2012

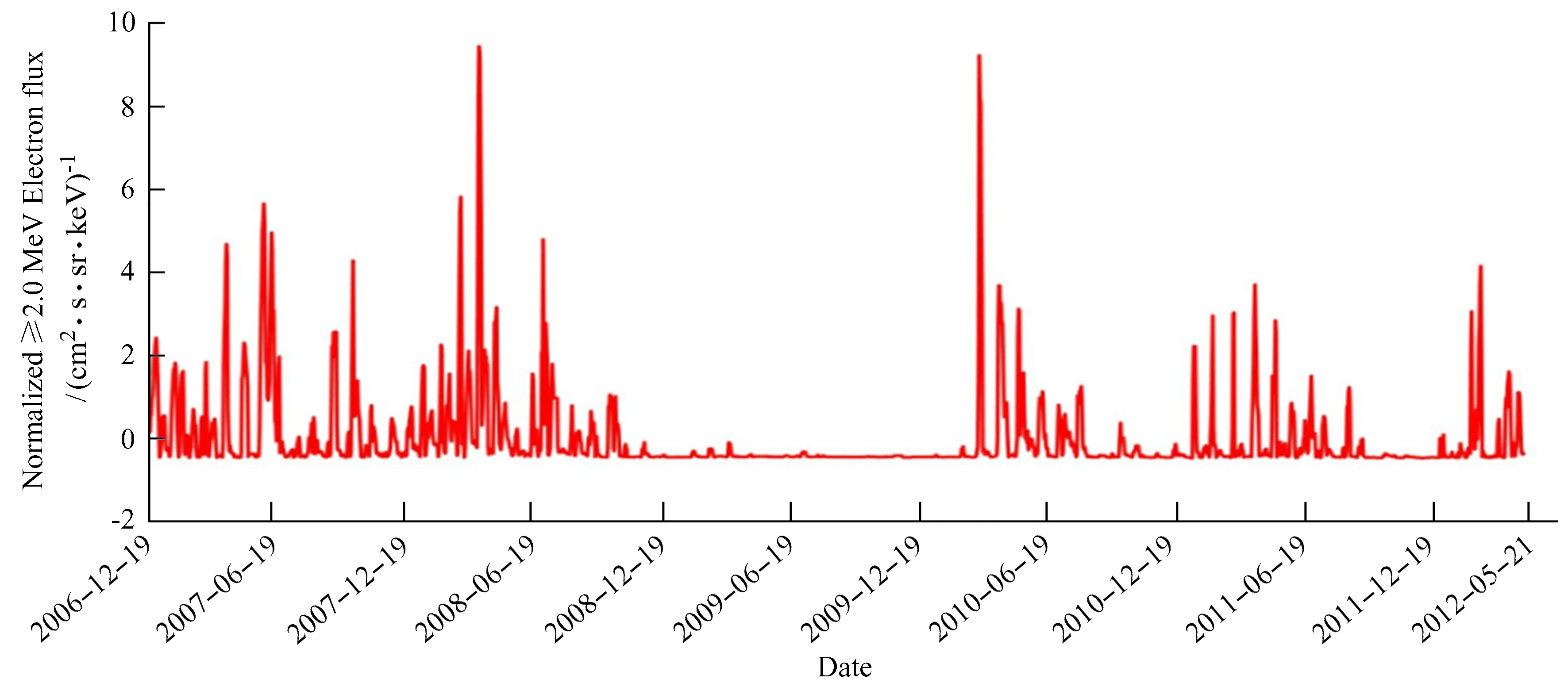
图3 归一化日平均通量图Fig.3 Normalized daily average flux diagram

3 高能电子通量的周期特性分析

为估计高能电子通量的周期特性[10]，本文选取2006年12月19日～2012年5月21日的日平均数据进行分析，分别采用最大熵谱法和Levinson-Durbin，Burg算法进行计算，对比分析三种方法的准确性。

3.1 自相关模型阶数选择与确定

由1.3可知，在选择自相关模型参数时，我们一般采用最终预报误差准则和赤池信息准则来判断。选择正确的自相关阶数是最大熵谱法的关键之一，阶数的大小能够影响我们判断熵谱图的波峰，继而影响周期的研究结果。

根据最终预报误差准则和赤池信息准则的计算公式，基于MATLAB实现最佳阶数的选择[11]，如图4，图4(a)和(b)分别是最终预报误差准则和赤池信息准则关于阶数和参数估计的关系。

图4两个子图的横、纵坐标分别为阶数和参数估值。用时间序列的最小二乘法和最终预报误差准则、赤池信息准则对自相关模型进行参数估计，再作折线图得到对应的最终预报误差准则和赤池信息准则的函数关系。由图4(a)和(b)对比可以看出，自相关模型阶数为10时，最终预报误差准则和赤池信息准则对应的参数估值均为最小值，分别为1 277 145.757和33 018.721 79，根据上述标准，运算结果符合(13)式。由此确定该自相关模型的最佳阶数为10。所确定的最佳阶数均适用于最大熵谱法和Levinson-Durbin, Burg算法。

3.2 高能电子通量周期特性分析

3.2.1 最大熵谱法

根据3.1确定的最佳阶数进行最大熵谱分析[12]。使用日平均数据作出的高能电子通量最大熵谱法功率谱如图5，阶数为10，高能电子通量周期分主、次周期[13]。根据功率谱概率分布可知，分布图存在多个峰值，本文选择研究最高波峰和次高波峰。最高波峰频率为0.062 5 d-1时，对应为主周期，功率谱最大为14.16，对应周期为13.87 d；次波峰频率为0.164 1 d-1时，对应为次周期，功率谱处于第二大值为13.71，对应周期为27.8 d。此研究结果与文[14]利用小波分析得出的高能电子通量的27 d和13 d周期结果一致，证明最大熵谱法研究高能电子通量的周期特性具有一定的准确性。

图5 最大熵谱法功率谱

尽管方法合理可行，也考虑了诸多因素，但是由于对数据进行了插值处理，经初步分析，计算结果大概存在0.03～0.08 d的误差。

此外，从图5可以明显看出，功率谱不止一个波峰，表明周期不唯一，且根据图像波峰变换的趋势也能判断其不稳定性[15]。

3.2.2 Levinson-Durbin算法和Burg算法

上文已经确定了最佳阶数为10，我们采用日平均处理后的数据进行周期特性分析。首先按照最佳阶数10绘制Levinson-Durbin，Burg算法的功率谱图像，与图5对比，图6中两图基本一致，再次证明阶数10为最佳阶数。观察图6可知，主周期频率为0.011 d-1，次周期频率为0.128 d-1，主次周期均与最大熵谱法结果不符。

图6(a)Levinson-Durbin算法的功率谱图；(b)Burg 算法的功率谱图Fig.6(a) Power spectrum diagram of Levinson-Durbin algorithm; (b) Power spectrum diagram of Burg algorithm

根据图6对比可知，高能电子通量确实存在周期性，且有多个周期，周期分为主、次周期，分别为13.87 d和27.8 d。与此同时，我们对比了最大熵谱法和Levinson-Durbin，Burg算法的分析结果，显示最大熵谱法的分析结果更接近真实值，更符合实际情况。

文[16-17]表明，电子通量13 d和27 d的周期与太阳活动密切相关。比如在太阳活动低年，横越赤道的冕洞产生高速太阳风，导致外辐射中电子通量发生变化，随着太阳自转，延伸型的冕洞每27 d旋转一周, 从而电子通量变化也具有27 d的周期。而电子通量13 d的周期也是伴随着太阳风速的变化产生的，在27 d周期中主要有3个相期：快速上升、峰值期和下降期，这种对称变化过程，即形成了13 d周期，所以一般在电子通量27 d的周期中存在13 d周期的变化成分。

4 结 论

本文基于风云二号D星探测的高能电子通量，利用最大熵谱法对周期特性进行了研究，得出以下结论：

(1)最大熵谱法表明，高能电子通量的主周期为13.87 d和27.8 d，且高能电子通量的周期不唯一，不稳定。

(2)通过最大熵谱法和Levinson-Durbin, Burg算法关于高能电子周期特性研究的比较，可以判断最大熵谱法更适合于高能电子周期的研究[18]，结果更接近真实情况。

(3)太阳活动影响高能电子的周期，随着太阳活动的变化，周期也发生相应变化。通过分析高能电子通量的周期变化可以侧面预测太阳活动的变化趋势，为日后研究太阳活动提供有价值的参考。