与活动区AR11158中的一个X2.2级耀斑相关的视向电流密度的计算*

杨丽平，梁红飞，刘继宏，王 楠，孙 霞，李子涵

(1. 云南师范大学物理与电子信息学院，云南 昆明 650500；2. 云南省高校高能天体物理重点实验室，云南 昆明 650500； 3. 中国科学院云南天文台，云南 昆明 650216；4. 石家庄学院物理学院机电学院，河北 石家庄 050035)

太阳耀斑是太阳大气中发生的高能爆发现象，爆发过程常伴随日冕物质抛射(Coronal Mass Ejection, CME)现象并向行星际释放大量的高能粒子流和磁云，是引起灾害性空间天气的主要因素[1]。因此，研究耀斑爆发机制对有效预防灾害性空间天气有非常重要的意义。研究表明，磁流浮现和对消[2]、黑子旋转[3-4]、剪切运动[5]是触发大耀斑爆发的3种主要机制，对活动区AR12673多个耀斑(包含一个X9.3级大耀斑)的研究[6]提出了一种新的耀斑爆发的触发机制，即由先前存在的磁场的阻挡引发的爆发模型。活动区AR12673在2017年9月4日至10日产生了包括4个X级耀斑、27个M级耀斑和57个C级耀斑在内的88个耀斑，强度最大的两个耀斑分别发生在9月6日(X9.3级)和9月10日(X8.2级)，X9.3级耀斑是第24个太阳活动周中最强的耀斑，爆发产生了很强的地球物理效应。因此，人们对该活动区进行了大量研究，相关研究结果表明，剪切运动和黑子旋转在触发两个连续的X级耀斑和日冕物质抛射中具有重要作用[7]，耀斑能量释放发生在中性线上方的低剪切磁环区域，光球的增量是由于耀斑产生的高能粒子轰击光球产生的[8]。在耀斑爆发过程中，磁重联被认为是能量快速释放的有效机制[9]，通常发生在剪切程度高的磁场区域[10]。在磁重联过程中，磁拓扑结构发生改变，磁能转化为加热等离子体的热能和加速粒子的动能。通常认为，磁重联最初的能量释放主要发生在日冕中，耀斑的爆发主要由磁重联释放的自由磁能驱动。自由磁能是指总磁能与势场磁能之间的差值，爆发耀斑的活动区磁位形偏离势场越大，活动区的总磁能与势场磁能的差值越大，活动区的非势性越强，储存的自由磁能就越多，耀斑产生的几率就越大[11]。光球及光球下方磁力线的剪切和扭绞，新浮现的磁流等都会形成活动区磁场的非势性[12]。由于磁中性线处的磁场梯度较大，磁场的纵向分量无明显变化，但水平磁场高度剪切，在磁压力的作用下产生大量的自由磁能，所以多数耀斑趋向于产生在磁中性线附近[13-14]。对5个X级耀斑的研究[15]发现，沿磁中性线的磁场剪切在耀斑之后有明显增强。最近基于高分辨率观测获得的矢量磁图的研究表明，在沿主要磁中性线有强剪切的活动区中存在大量净电流[16]。文[17]对活动区电流分布的研究表明，能够驱动日冕物质抛射和耀斑的活动区具有大量净电流，与最近的观测结果一致，而且耀斑带的位置和形态与光球层强电流带有密切关系，在耀斑演化过程中，耀斑带的形态改变可能与电流带相关[18]。太阳活动区中电流密度较高的区域[19]与Hα耀斑核块及具有极大剪切的磁场区域重合[20]，这个结果支持耀斑是由强电流引起的等离子体的不稳定性触发的理论[21]。这些研究都证实了电流可能在耀斑爆发之前就已存在，并在耀斑爆发过程中起重要作用，活动区中电流带与耀斑带之间密切相关。因此，计算活动区磁中性线两侧强磁场中的电流分布对于预测耀斑爆发的位置和形态具有重要意义。

随着观测仪器的时间和空间分辨率不断提高，人类对太阳爆发活动机制有了比较深入的了解，其中，准确的矢量磁场测量对研究太阳爆发活动的触发机制非常重要。太阳矢量磁场的测量是基于塞曼效应进行的，由于来自日冕、过渡区等太阳大气的偏振信号非常弱，因此，这些区域的矢量磁场很难获得，目前唯一能够精确测量磁场的区域只有光球层。基于测量的光球层磁场结构，人们以此为边界条件利用非线性无力场[22]模型进行外推，获得三维空间矢量磁场的可能结构。由于无法准确测量日冕层的矢量磁场，也就几乎不可能准确计算日冕中的电流分布。基于精确测量的光球矢量磁图，我们可以利用安培定律计算光球层的视向电流密度分布。由于观测仪器在测量矢量磁场的过程中不可避免地受到系统误差和随机误差的影响，系统误差主要来源于对太阳大气的相关参数所做的假设和简化、仪器散光和镜片的非正常反射、系统性的相干。随机误差主要由大气视宁度、观测仪器电噪声等引起[23]。系统误差可以在某种程度上从原始数据中消除或采用如暗场处理、平场处理等减小它们对结果的影响，无法消除的那部分系统误差在整个视场是连续可导函数，它们对电流的影响也有一定规律。而随机误差在不同的空间格点上随机变化，不能从原始数据中消除，通常服从正态分布，这给我们利用安培定律微分算法计算视向电流密度带来很大的障碍。文[24]通过在矢量磁场中引入随机噪声，研究了随机噪声产生的影响和空间分辨率之间的关系，并分析微分法、小环路积分法和大环路积分法得到的结果，他们发现当忽略高阶项时，沿一个大环路的安培定律的积分形式计算电流密度分布得到的结果最好。为了进一步验证文[24]的结果，并检验耀斑带和电流带的对应关系，我们利用太阳动力学天文台[25]/日震学与磁场成像仪[26]在2011年2月15日观测到的活动区AR11158的矢量磁场，利用安培定律的4种形式(微分形式、小环路积分、中环路积分和大环路积分)计算该活动区的视向电流分布，将积分法的积分环路扩大到适当的大小进行比较。我们还考察了计算结果的电流密度极值与耀斑带的位置和形态的对应关系，以检验计算电流密度方法的有效性和合理性。

1 数据来源和计算方法

1.1 数据来源

日震学与磁场成像仪、大气成像组件(Atmospheric Imaging Assembly, AIA)[27]以及远紫外光谱仪(EUV Variability Experiment, EVE)是搭载在太阳动力学天文台卫星上的3台仪器。通过日震学与磁场成像仪可以获得太阳光球层的矢量磁场、光球强度以及多普勒速度等相关数据。2011年2月15日位于太阳西南方向(S20W12)的活动区AR11158具有βγ结构的复杂磁位型，在1:44～02:06UT期间该活动区爆发了一个持续约22 min的X2.2级耀斑，有关该活动区的研究可参考文[28-29]。在本文中，我们通过日震学与磁场成像仪获得其在耀斑爆发期间观测的磁场数据，空间分辨率为0.5 ″/pixel，时间分辨率为45 s/frame。矢量磁场的测量是基于塞曼效应利用偏振辐射转移方程获得，获得矢量磁场数据的具体过程见文[30]，日震学与磁场成像仪利用斯托克斯(Stokes)矢量的快速反演技术VFISV(Very Fast Inversion of the Stokes Vector)[31]得出矢量磁图，时间分辨率为12 min/frame。由于以偏振辐射转移方程为理论基础求解矢量磁场的过程中往往存在方位角180°不确定性问题，给太阳磁场的测量带来很大的障碍。为了解决这个问题，势场校准法[32]、无力场近似法[33-34]、最小能量法[35]、磁荷法[36]、连续性方法[37]等先后提出并得以完善，从而很好地解决了太阳磁场测量中的方位角180°不确定性问题。在利用日震学与磁场成像仪测量的活动区偏振信号反演矢量磁场的过程中，太阳动力学天文台研究团队利用能量最小法对矢量磁场数据进行预处理，解决了矢量磁图中方位角180°不确定性问题[35]，使得太阳磁场的相关研究得以顺利进行。

大气成像组件是用于观测不同高度的太阳大气层的仪器，可以同时提供10个不同波段的太阳大气信息。这10个波段包括7个极紫外波段(EUV)、2个紫外波段(UV)和1个可见光波段(连续谱450 nm)。其中极紫外波段包括30.4 nm，17.1 nm，19.3 nm，21.1 nm，33.5 nm，9.4 nm和13.1 nm；紫外波段包括170 nm和160 nm。各波段在大气中对应的谱线及观测区域在文[27]中进行了详细介绍。大气成像组件图像的空间分辨率为0.6 ″/pixel，时间分辨率分别为12 s/frame(极紫外波段)，24 s/frame(紫外波段)。本文所用大气成像组件数据是170 nm波段和30.4 nm波段，其中，170 nm波段的观测区域为温度极小区和光球层，30.4 nm波段的观测区域为色球层和过渡区。

1.2 计算方法

图1(a)为活动区AR11158在2月15日02:00:00UT时刻的纵向磁图，其中，白色为正极磁场，黑色为负极磁场，黑色框所围区域内存在一对极性相反的磁极，红色箭头所指位置为正负磁极分界的磁中性线，如图1(a)和(b)中黄色虚线位置，磁中性线的上方为一个椭圆形负磁极，下方为一个半月形正磁极，在磁中性线附近磁场的梯度非常大。通常磁中性线也称作纵向磁场的极性变换线，是正负极磁场的分界线。图1(b)为活动区在2月15日02:00:00UT时刻日震学与磁场成像仪观测到的矢量磁图。为了能够清晰地看出矢量磁场的结构，图中以纵向磁场为背景，叠加在纵向磁场上方的小箭头表示横向磁场，其中蓝色箭头覆盖区域为正极磁场，红色箭头覆盖区域为负极磁场，箭头长度表示横向磁场的大小，箭头方向表示横向磁场的方向，灰度图与图1(a)完全相同，均表示纵向磁场的大小。从表示横向磁场的箭头簇不难看出，横向磁图具有旋涡状结构，这种结构意味着活动区内可能存在比较强的电流。我们基于这些矢量磁图利用安培定律的不同形式计算活动区内的电流密度分布，并比较和分析不同方法计算结果的差异，从而挑选一种最优的电流密度计算方法。太阳动力学天文台除了提供该活动区的矢量磁图外，还在不同波段采集到了活动区的单色像。图1(c)和(d)为大气成像组件分别利用谱线170 nm(01: 58: 08UT)和30.4 nm(01: 58: 12UT)观测到的2011年2月15日在活动区AR11158产生的X2.2级耀斑的单色像图。从图中可以看出，耀斑带主要在黑色方框区域内，部分结构位于方框的右上沿，对比图1(a)，(c)和(d)不难发现，耀斑主要位于磁中性线附近。

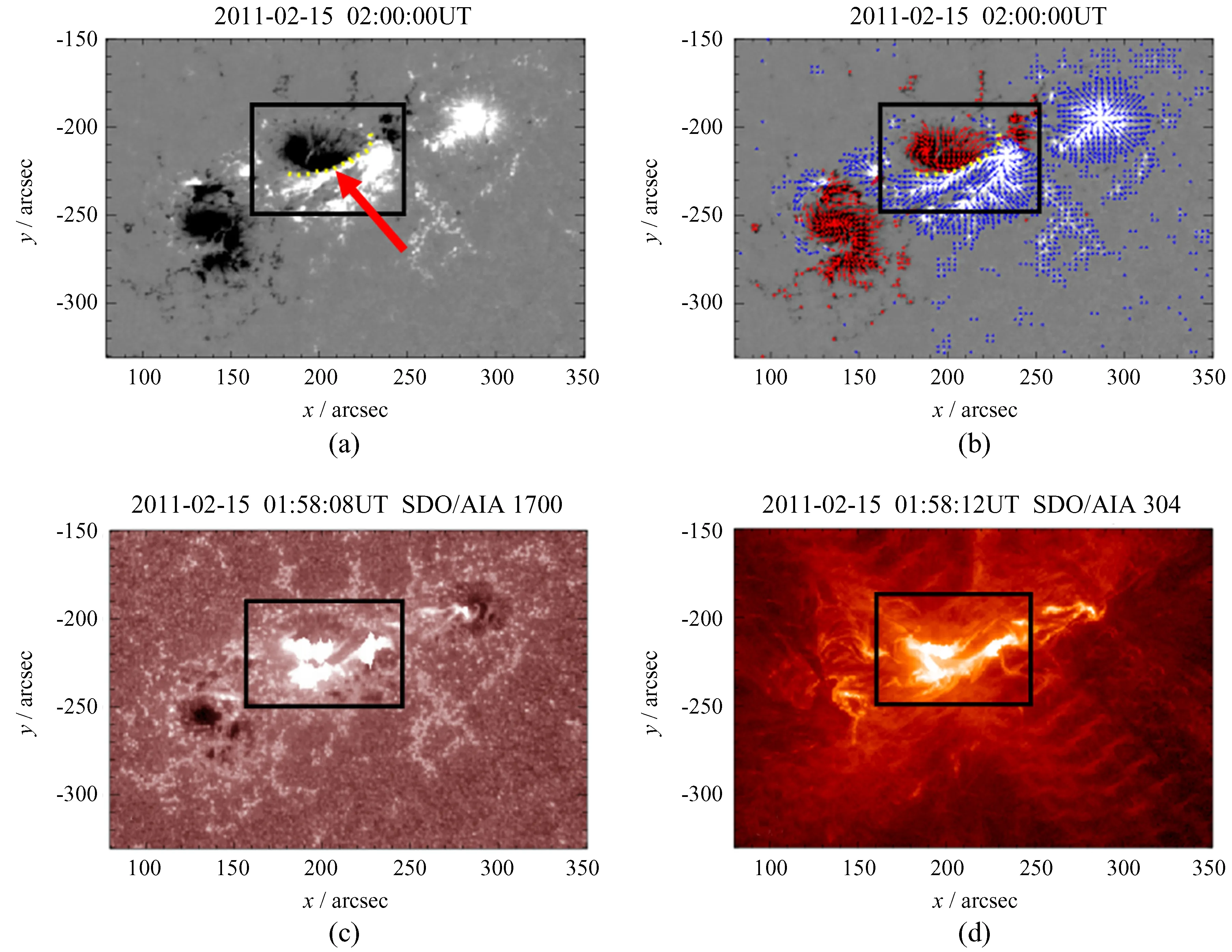
图1 (a)活动区AR11158的纵向磁图；(b)矢量磁图；(c)170 nm波段的单色像图；(d)30.4 nm波段的单色像图

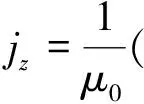
(1)

计算视向电流密度jz，其中，μ0为真空中的磁导率。如图2，利用Bx，By在最里面的小正方形4条边上的中点A(x+ Δx,y)，B(x,y+ Δy)，C(x- Δx,y)和D(x,y- Δy)的值进行计算，差分公式变为

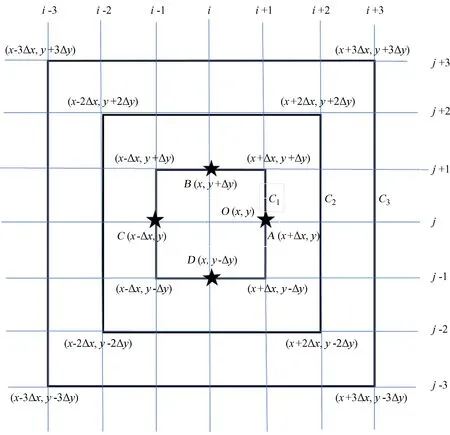
图2 安培定律积分形式的积分路径：内部最小的正方形为积分路径C1，由内向外第2个正方形为积分路径C2，第3个正方形为积分路径C3。位于C1上的4个有星号的点对应于安培定律的差分形式，即基于横向磁场Bt在A[x + Δx, y]，B[x, y + Δy]，C[x - Δx, y]和D[x, y - Δy]点的值可通过安培定律的差分形式计算[x, y]处的视向电流密度

(2)

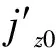
(3)

由(3)式可知，当随机噪声δBx和δBy不变时，Δx和Δy随着空间分辨率的增大而减小，最终导致误差电流密度增加并将真实电流密度淹没，所以我们通常用安培定律的积分形式

(4)

计算视向电流密度，其中，Bt为实测横向磁场，Bt=eiBx+ejBy,ei,ej,Bx,By分别是x，y方向的单位矢量及实测横向磁场的两个分量；ds为积分路径l所围的面积，通常选择边长为nΔx的正方形为积分路径，n为空间格点数，则Δs=n(Δx)2。由(4)式可知，Δx随着矢量磁场空间分辨率的变化而变化，分辨率越高环路需要扩得越大，分辨率越低环路需要扩得越小，通过分辨率的高低来选择适当大小的积分环路可以快速降低随机噪声对计算结果的影响。通常根据分辨率的大小来定义小环路、中环路和大环路。

如图2，环路积分法是利用横向磁场Bt在积分路径上的值计算积分环路所围面积内的平均电流密度，得出积分环路中心O(x,y)点的电流密度，所得电流密度为积分区域的平均电流密度。积分路径沿逆时针方向，积分环路以O(x,y)为中心由小到大(或由内向外)依次称为小环路(以2Δx为边长的正方形，积分路径为C1)、中环路(以4Δx为边长的正方形，积分路径为C2)和大环路(以6Δx为边长的正方形，积分路径为C3)。其中，小环路的积分路径是沿点(x+ Δx,y+ Δy)，(x- Δx,y+ Δy)，(x- Δx,y- Δy)和(x+ Δx,y- Δy)所在的正方形边缘，积分路径为C1，对应的视向电流密度为jz1。由(4)式可得小环路的计算公式为

(5)

其中，ds=2Δx2Δy。

中环路的积分路径是沿点(x+ 2Δx,y+ 2Δy)，(x- 2Δx,y+ 2Δy)，(x- 2Δx,y- 2Δy)和(x+ 2Δx,y- 2Δy)所在的正方形边缘，积分路径为C2，对应的视向电流密度为jz2。由(4)式可得中环路的计算公式为

(6)

其中，ds=4Δx4Δy。

大环路的积分路径是沿点(x+ 3Δx,y+ 3Δy)，(x- 3Δx,y+ 3Δy)，(x- 3Δx,y- 3Δy)和(x+ 3Δx,y- 3Δy)所在的正方形边缘，积分路径为C3，对应的视向电流密度为jz3。由(4)式可得大环路的计算公式为

(7)

其中，ds=6Δx6Δy。

2 结 果

图3是分别利用安培定律的微分法和环路积分法计算的耀斑爆发期间(02: 00: 00UT)的视向电流密度分布图。图中用 “Dif” 表示差分法，用 “Int” 表示积分法， “C1” 表示小环路， “C2” 表示中环路， “C3” 表示大环路。图中白色和黑色分别表示正负电流密度分布，对应的视向电流密度分别为+0.05 A·m-2和-0.05 A·m-2。为了便于比较和分析，我们在微分法和积分法中所取的视向电流密度阈值相同，均为±0.05 A·m-2。图3(a)和(b)分别是利用安培定律的微分法和积分法(小环路)计算的视向电流密度分布图，图3(c)和(d)是扩大积分环路时计算的视向电流密度分布图，其中(c)为中环路的计算结果，(d)为大环路的计算结果。由于所测矢量磁图中的横向磁场不可避免地受随机噪声的影响，微分法计算的电流密度分布(如图3(a))受噪声信号影响较大，相比之下，小环路积分法(如图3(b))计算的电流密度分布受随机噪声的影响较小。当把积分环路扩大到两个(中环路，如图3(c))时，得到的电流密度分布比小环路积分法计算的噪声信号更小。当把积分环路扩大到三个(大环路，如图3(d))时，虽然计算的噪声信号更小，但电流密度分布中的部分精细结构明显失真。因此，在考虑随机噪声的情况下，我们选择扩大积分环路的方法，并将积分环路扩大到两个，即利用中环路积分方法计算视向电流密度更好。

由图3(c)和图1(a)可以看出，强电流主要产生于磁中性线附近的强磁场区域，与强磁场有很好的对应关系。由图1(a)，(c)和(d)可以看出，耀斑带可能出现在磁中性线附近的区域，说明电流带与耀斑带在位置上可能具有某种对应关系。如图4，我们通过做投影改正将中环路积分法(如图3(c))计算的视向电流密度分布与相同耀斑时刻的170 nm波段和30.4 nm波段的单色像图(图1(c)和(d))对齐，图中绿色和蓝色等高线分别表示正负电流带，对应的视向电流密度分别为+0.02 A·m-2和-0.02 A·m-2。结果显示，耀斑带大致出现在电流较强的位置，此处的自由磁能多，释放的能量也多，而且耀斑带与电流带具有相似的形态。

图3 安培定律的微分算法和积分算法计算的视向电流密度分布图

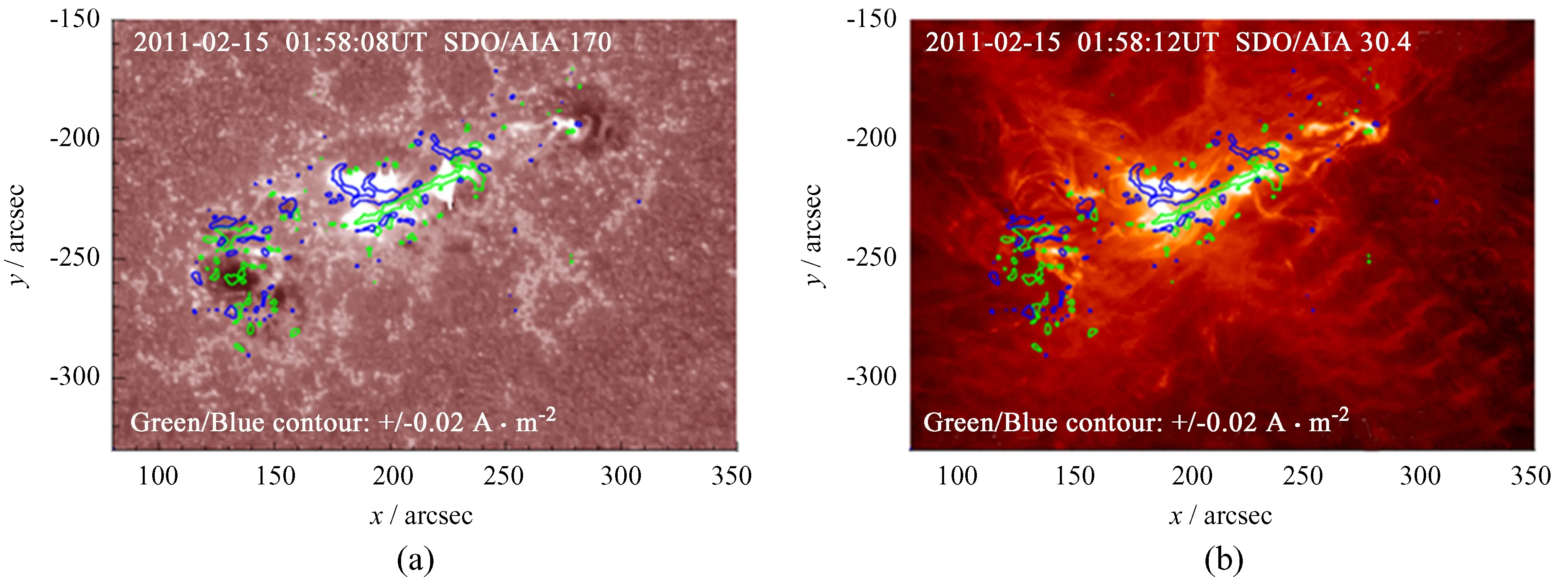
图4 电流带与耀斑带的对应关系，(a)为大气成像组件170 nm波段在2011年2月15日01:58:08UT时刻活动区的单色像图；(b)为大气成像组件30.4 nm波段在2011年2月15日01:58:12UT时刻活动区的单色像图，图中的绿色等高线和蓝色等高线分别表示正极和负极电流带，对应的视向电流密度分别为+0.02 A·m-2和-0.02 A·m-2

3 讨论与结论

太阳耀斑究竟在什么位置爆发，其形态是什么样的，如何寻找一种有效预测太阳耀斑爆发位置和形态的方法一直是太阳物理中的前沿课题。耀斑爆发与活动区电流有着密切的联系，活动区的电流主要表现为由矢量磁图中横向磁场的变化产生的视向电流。因此，选择一种有效计算活动区视向电流的方法显得尤为重要。在不考虑随机噪声的情况下，随着空间分辨率的提高，利用安培定律的微分形式和积分形式计算的视向电流密度比较接近。在考虑随机噪声的情况下，利用安培定律的微分形式计算视向电流密度，虽然计算量小，但随着空间分辨率的提高(空间格点宽度Δx和Δy变小)，由随机误差引起的电流密度的离散度变大，计算的视向电流密度的不确定性也在增加[41]。即使将视向电流密度分布图进行平滑处理，在消除噪声信号的同时也会把原来噪声信号覆盖下的电流信号消除。而利用安培定律的积分形式计算视向电流密度，虽然比微分形式计算量大，但可以降低测量值的离散度，使计算结果受随机误差的影响变小。若扩大积分环路，矢量磁场的空间分辨率降低(空间格点宽度Δx和Δy变大)，可以快速降低测量值的离散度，所得结果更准确。利用安培定律的积分形式计算视向电流密度的方差比微分形式计算的电流密度的方差更小[42]。当积分路径超过所研究矢量磁图的最小空间分辨率结构的线性大小时，所得电流密度分布的部分精细结构失真。基于高分辨率矢量磁图寻找一种合适的积分路径计算视向电流密度，能在去除噪声信号的同时保留原有的电流信号，所得结果更准确。

基于此理论，本文通过比较计算视向电流密度的几种方法，即安培定律的微分算法、小环路积分法、中环路积分法和大环路积分法(如图3)，最终得出这样的结论：在考虑随机噪声的情况下，选择安培定律的积分算法，并将积分环路扩大到第2个时计算的视向电流密度分布图更清晰，而且电流精细结构不失真。由图4可以看出，耀斑带与电流带的爆发位置和形态极其相似，所以，计算的视向电流密度分布对于准确预测耀斑爆发的位置和形态具有非常重要的意义。为了从理论上分析积分路径是否合适，模拟时可以在矢量磁场中设定一个电流密度的真实值，但本文中的数据是通过空间采样所获得的观测数据，由于受随机噪声的影响无法确定电流密度的真实值，所以文中用实际观测的数据验证[24]模拟方法的准确性，即用扩大积分环路(本文中为中环路)的方法得到的电流密度分布图效果最好。同时我们可以利用所计算的视向电流密度分布预测耀斑爆发的可能位置和形态，也验证了计算视向电流密度方法的有效性和可靠性。未来我们将利用大气成像组件其它波段的观测数据对多个活动区的耀斑带和电流带进行研究，以检验该方法的合理性和普适性。