一类差分方程退化不动点的定性性质

李明山， 周效良

（1.南京航空航天大学 经济与管理学院，江苏 南京211106； 2.岭南师范学院 数学与统计学院，广东 湛江524048）

近年来，差分方程理论与应用研究取得许多成果［1-4］.目前关于二维差分方程具有特征值±1的退化不动点的定性性质研究成果较少.文献［5］利用Picard迭代［6］、去奇化理论［7］、共轭关系［8］和Takens定理［9］研究了一类离散竞争模型退化不动点的定性性质.文献［1］提出了一类离散经济模型

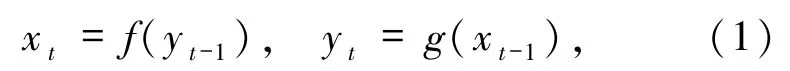
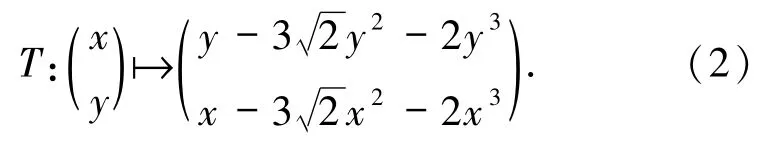
映射（2）在不动点E0（0，0）处的特征值为 λ1＝1，λ2＝－1.本文考虑映射（2）在退化不动点E0附近的定性性质.

本文利用Picard迭代和Takens定理得到了映射（2）在退化不动点E0的近似系统（也称为微分方程），通过极坐标变换来研究微分方程在退化平衡点附近的定性性质.进一步，利用blow-up方法和微分方程的时间-1映射的反射与映射（2）之间的共轭来研究映射（2）在退化不动点E0附近的定性性质.

1 流近似

利用Picard迭代和Takens定理将映射嵌入微分方程的流.利用微分方程来研究映射（2）在退化不动点E0处的定性性质，首先给出Takens定理.

引理1.1［9］假设

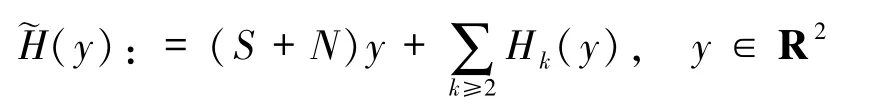
是一个在O附近的形式映射，S是半单的且具有特征值 ±1，N是幂零的，是k次齐次多项式，则在O附近存在唯一的不变向量场Y使得φ~Y（1，·），这里 φ~Y（t，·）表示~Y的形式流.对所有）仅依赖于j k（~H），其中j k是截断形式映射或者形式向量场在O处的k次项系数.

定理1.2在（0，0）的充分小邻域内，映射R◦满足

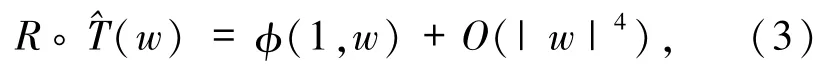
其中，w＝（u，v），R＝diag（1，－1），φ（t，w）满足初值φ（0，w）＝w，并且是由如下平面微分方程生成的流

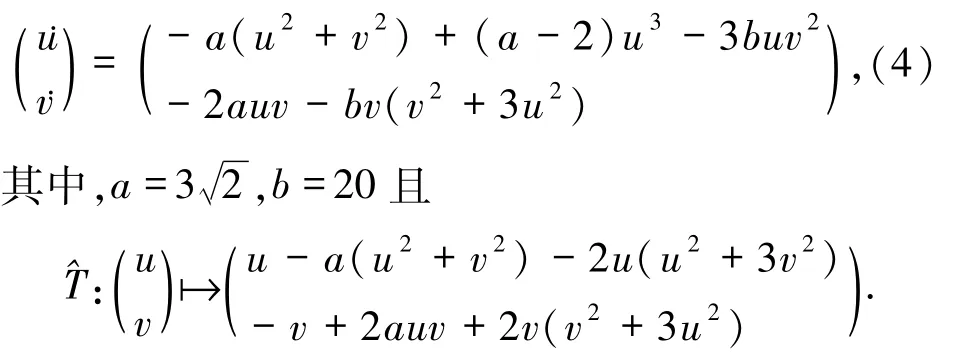
证明利用ϑ：x＝u＋v，y＝u－v变换可将映射（2）对角化为T＾，故有

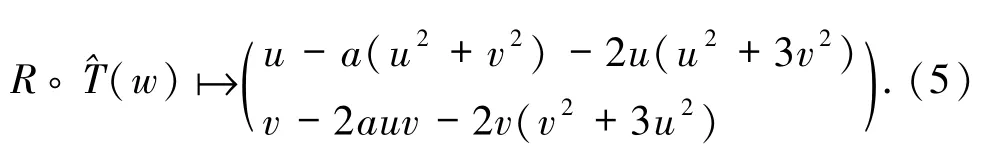
由Takens定理，映射在E0附近可以嵌入连续流.考虑如下微分方程

其中Xk（u，v）∈Hk，

a ij、bij是待定的.设微分方程（6）有如下形式

接着比较（7）式和（8）式的三次项可得

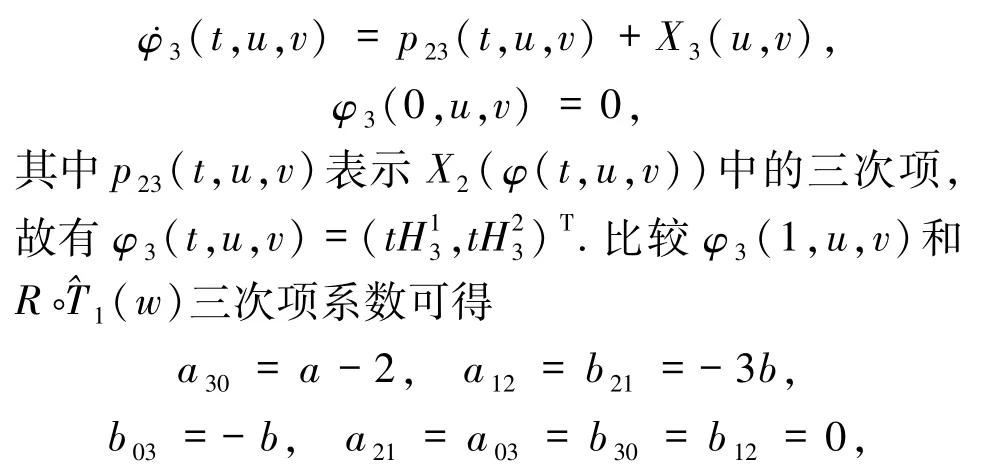
故映射R◦（w）的近似系统为微分方程（4）.证毕.

这样就得到如下向量场：

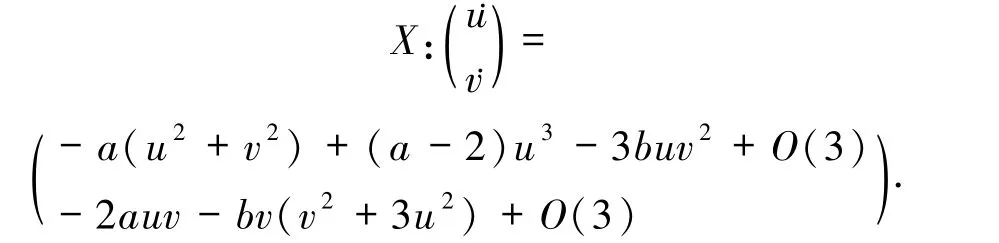
为方便行文，给出如下记号，其中אi、Ik（i，k∈υ）是以E0为中心的扇形邻域是充分小的正数，υ：＝ ｛1，2，3，4｝，κ：＝｛j＋1｝，且

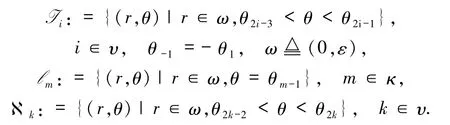
定理1.3微分方程（4）的平衡点（0，0）是不稳定的.在E~0充分小邻域附近，在区域I1内，微分方程（4）的轨线沿着直线I1进入E~0，区域I1是一个吸引的扇形区域；在区域I2内，微分方程（4）的轨线沿着直线I2靠近平衡点E~0，并且沿着直线l4离开平衡点，区域I2是一个鞍点扇形区域；在区域I3内，微分方程（4）的轨线离开平衡点E~0，区域I3是一个排斥的扇形区域；在区域I4内，微分方程（4）的轨线沿着直线l8靠近平衡点E~0，并且沿着直线l5离开平衡点，此时区域I4是一个鞍点扇形区域.

证明为了明确微分方程（4）在原点附近的轨线走向，对其实施坐标变换x＝rcosθ，y＝rsinθ，得到如下系统

系统（10）在单位圆周｛0｝×S1上有奇点（0，θj），j＝1，2，…，8.若r充分小，当 θ ＝ θ0时，有 θ˙＝0.此时r˙＜0，所以在l1直线上（4）式的轨线是趋向于平衡点E~0.当 θ∈（－ θ1，θ1）时，有r˙＜0.所以在区域I1内，（4）式的轨线沿着直线I1进入平衡点E~0，此时区域I1是一个吸引的扇形区域.当θ∈（θ1，θ2）时，有r˙＜0.当 θ∈（θ2，θ3）时，有r˙＞0.所以在区域I2内，（4）式的轨线沿着直线I2靠近平衡点E~0，并且沿着直线l4离开平衡点，区域I2是一个鞍点扇形区域.当 θ＝ θ4，u＜0时，此时r˙＞0.所以在l4直线上（4）式的连续时间流是趋于－∞的，从而（4）式的平衡点E~0是不稳定的.当 θ∈（θ3，θ5）时，有r˙＞0.所以在区域I1内（4）式的轨线离开平衡点，此时区域I3是一个排斥的扇形区域.

因为（4）式是v↦－v不变的，所以在区域I2内，（4）式的轨线沿着直线l6靠近平衡点E~0，并且沿着直线l6离开平衡点此时区域I4是一个鞍点扇形区域，故（4）式在平衡点附近的相图如图1所示.证毕.

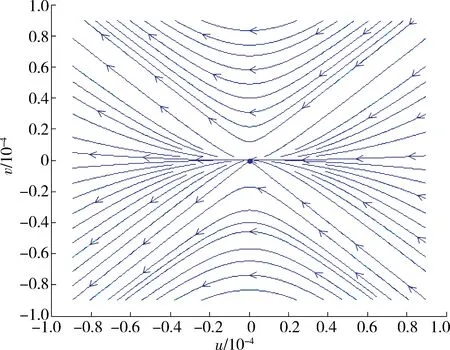
图1 （4）式在平衡点~E 0附近的相图Fig.1 Phase portrait of system（4）near equilibrium~E 0

2 退化不动点的定性性质与稳定性

下面应用blow-up方法来研究向量场X的平衡点的定性性质.应用映射（2）与向量场X之间的共轭关系，得到了映射（2）退化不动点E0的定性性质.

引理2.1［8］设H和Y分别是在原点O附近的C∞映射和C∞向量场，且它们的形式部分分别与引理1.1给出的形式映射~H和形式向量场~Y相同.假设向量场Y有一轨道沿着特定的方向连接O，向量场Y无椭圆扇形，且向量场Y是Lojasiewicz类型的.假设通过去奇化后得到的向量场仅有双曲平衡点，则存在C∞坐标变换Ψ满足j∞（Ψ－I）＝0使得 Ψ－1◦H◦Ψ ＝S◦φY（1，·），其中I表示恒同变换.

若存在常数k、σ、η 使得对任意（x，y）∈R2，‖（x，y）‖k≤η，都有‖Y（x，y）‖≥σ ‖（x，y）‖k，则称C∞向量场是Lojasiewicz类型的，其中‖·‖表示R2中的Euclid范数.显然向量场X是Lojasiewicz类型的.

定理2.1映射（2）的退化不动点E0是不稳定的.在退化不动点E0的充分小邻域内，若初值Q（x0，y0）∈א1，则沿着直线l2两侧收敛于E0，א1是一个“吸引的扇形区域”；若初值Q（x0，y0）∈א2，则沿着直线l3靠近不动点E0，并且沿着直线l5离开不动点E0，区域א2是一个“鞍点扇形区域”；若初值Q（x0，y0）∈א3，则离开不动点E0，区域א3是一个“排斥的扇形区域”；若初值Q（x0，y0）∈א4，则沿着直线l1靠近不动点E0，并且沿着直线l7离开不动点E0，此时区域א4是“排斥的扇形区域”.

证明显然微分方程（4）与向量场X在原点O附近的定性性质是一样的.对向量场X应用变换u＝w1，v＝w1w2沿着v轴进行blow-up，将向量场X转化为如下系统

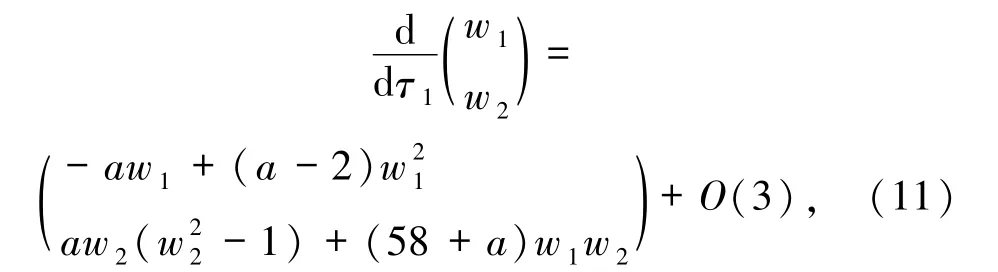
这样可以降低向量场X平衡点（0，0）的退化程度，其中dτ1＝w1dt.系统（11）在w2轴有平衡点E4（0，0）、E5（0，1）和E6（0，－1），在平衡点处E4、E5和E6的雅可比矩阵分别为

故平衡点E4是稳定结点，平衡点E5和E6是鞍点.对微分方程（4）应用变换u＝ξ1ξ2，v＝ξ2沿着u轴进行blow-up，得到如下系统

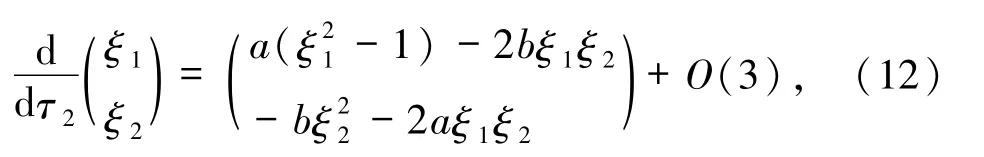
其中dτ4＝ξ2dt.系统（12）在 ξ1轴有平衡点E7（－1，0）和E8（1，0），在平衡点E7的雅可比矩阵为J（E7）＝diag（－2a，2a）且J（E8）＝ －J（E7），故平衡点E7和E8是鞍点.

由上述过程可知，向量场X经过去奇化获得的系统只有双曲平衡点，所以对于向量场X，由定理1.2可知向量场X满足引理2.1的假设条件.由引理2.1可知，在O附近存在一个C∞微分同胚Ψ2满足j∞（Ψ2－I）＝0使得

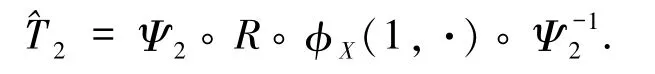
图2 映射（2）在平衡点E 0附近的相图Fig.2 Phase portrait of mapping（2）near equilibrium E 0

本文研究一类差分方程退化不动点E0的定性性质.微分方程（4）的退化平衡点比较复杂，出现了鞍点扇形，这是文献［5］中所没有涉及的情形.

致谢广东省大学生科技创新培育专项资金（PDJH2021B0309）、广东省高校重点项目（2019KZDXM032）和南京航空航天大学研究生创新基地（实验室）开放基金（KFJJ20190802）对本文给予了资助，谨致谢意.