TiB纤维分布的均匀性对钛基复合材料拉伸性能的影响
2021-07-14黄立清丁永峰
黄立清,李 超,郭 薇,丁永峰,李 健,3
(1.湖南金天钛业科技有限公司 湖南省高端装备特种钛合金工程技术研究中心,湖南 常德 415001)
(2.龙岩学院, 福建 龙岩 364012)
(3.福建省焊接质量智能评估重点实验室, 福建 龙岩 364012)
轻质高强的零部件有利于促进机械装备的减重,从而有效地提高能源利用效率,在汽车、飞机、能源动力等领域具有重要应用。轻质高强零部件的开发主要依赖于高强韧结构材料的应用。在金属材料领域,复合材料强化法被普遍认为是既能有效提升材料强度、刚度与硬度,又能在一定程度上保持金属基体固有塑性的办法[1,2]。连续纤维增强金属基复合材料具有高的强度和刚度,而非连续纤维/颗粒增强金属基复合材料具有各向同性的优点。
对于非连续增强钛基复合材料,由于钛本身为活泼属性,可通过原位自生法获得TiB短纤维、TiC颗粒及Ti5Si3颗粒等增强钛基复合材料[3, 4]。通常,可通过将硼化物、碳化物及硅化物等粉末与钛粉或钛合金粉进行机械合金化,然后对复合粉末进行热压、放电等离子烧结或热挤压等制备致密的钛基复合材料[5, 6]。在烧结的过程中,钛粉与硼化物、碳化物及硅化物等颗粒发生化学反应而快速生成增强相TiB短纤维、TiC颗粒及Ti5Si3颗粒等。然而,由于钛粉的性质过于活泼,高能的机械合金化过程给钛粉末或钛合金粉末带来较大的污染;因污染而引入的杂质元素(O、N)在钛基体中具有强的强化与脆化作用,使得机械合金化制备法的过程难以控制且最终产品的塑性差[7]。L J Huang等[8]避开机械合金化,通过将钛合金粉与硼化物粉末进行简单的机械混合后进行热压,制备了一种具有网状分布的TiB短纤维增强钛基复合材料,获得较高的抗拉强度并保持有钛基体一定的塑性。L Q Huang等[9, 10]通过将钛粉或钛合金粉与纳米硼化物粉末进行简单的机械混合,然后在不同的温度区间进行放电等离子烧结,获得了具有网状编织分布的TiB纤维(长度5~30 μm)增强钛基复合材料,且其具有高的韧性。这些研究证实了该类制备方法是当前制备非连续增强钛基复合材料的最佳选择之一。
受制于加工工艺、增强相的形状及尺寸、增强相与基体的种类及增强相与基体之间的界面结合情况,增强相的分布对于金属基复合材料的抗拉伸强度和塑性的影响比较复杂。相比于均匀分布,增强相的非均匀分布形式会提高或降低或基本不影响金属基复合材料的强度与塑性均可见报道[11-14]。因此,在前期研究工作的基础上,进一步研究原位自生的TiB短纤维在钛基体中的分布均匀性对钛基复合材料拉伸性能的影响,以进一步优化钛基复合材料的性能。
1 实 验
实验原料为2种不同粒径(分别为0~45 μm和75~106 μm)的球形等离子雾化高纯钛粉,纯度均≥99.8%。在2种钛粉中分别添加体积分数(x)为5%、7.5%和10%的高纯纳米B粉(纯度≥99.6%,尺寸<100 nm),然后装入混料器(Turbula mixer)中进行低能机械混合。对混合均匀的粉末进行放电等离子烧结,制备TiB纤维增强钛基复合材料。下文将采用SmallTi-xTiB与LargeTi-xTiB分别代表采用0~45 μm和75~106 μm钛粉制备的复合材料。此外,以2种纯钛粉直接进行放电等离子烧结制备的纯钛试样作为参照。复合材料制备过程中,混料工艺为:氩气保护,转速120 r/min, 球料比2∶1,混合时间2 h;烧结工艺为:烧结温度1200 ℃,压力30 MPa,保温时间5 min。
为更好地观察TiB纤维在钛基体中的分布,对机械抛光后的复合材料进行深度腐蚀,移除部分钛基体。腐蚀液的成分为86%纯水+10%硝酸+4%氢氟酸,腐蚀时间为5 min。通过金相显微镜(Leica DM2700M)观察复合材料钛基体的晶粒尺寸;通过扫描电子显微镜(JEOL JSM 7001F)观察复合材料中纤维形貌及分布;通过氧氮氢分析仪(TCH-600 O,N and H analyzer)测试复合材料中O、N含量;通过拉伸试验机(Instron-5584)测试复合材料的拉伸性能。拉伸试样的标距为8 mm,拉伸速率为10-3s-1。
基于本实验中获得的钛基复合材料的组织结构及材料性质,构建TiB纤维均匀分布和非均匀分布增强钛基复合材料的模型,并进行仿真计算。复合材料具有周期性边界条件的代表性体积单元通过Python程序构建,代表性体积单元被导入Abaqus软件并进行隐式求解。模型中,钛基体的弹塑性参数由本研究中的实验结果所得,泊松比则参考文献资料为0.34[15];TiB纤维的杨氏模量为427 GPa[16],泊松比为0.15[16]。此外,由于Ti/TiB界面具有共格属性[17],模型中选用的Ti/TiB界面为紧密结合界面。
2 结 果
2.1 实验结果
金相观察下,制备的复合材料均全致密,且Ti基体的晶粒尺寸均约为15 μm。其中,采用细钛粉制备的SmallTi-xTiB复合材料中氧含量约为0.20%,氮含量<0.01%(质量分数,下同);而采用粗钛粉制备的LargeTi-xTiB复合材料中氧含量约为0.16%,氮含量<0.01%。SmallTi-xTiB复合材料的氧含量稍高于LargeTi-xTiB,这主要是由于钛粉末越细小,比表面积越大,制备过程中更容易被污染。
图1为SmallTi-7.5TiB和LargeTi-7.5TiB复合材料被深度腐蚀后的显微形貌。2种复合材料中,TiB短纤维的尺寸基本一致,平均长度约为30 μm,直径约为2 μm(因TiB纤维的横截面为六边形[8, 9],此处直径为六边形的外接圆直径)。在由粗钛粉制备的LargeTi-7.5TiB复合材料中(图1c、1d),TiB纤维形成了一种中空的网状分布结构。这种结构是由于TiB在钛粉原始颗粒边界形核并向周围生长而形成的[9]。在由细钛粉制备的SmallTi-7.5TiB复合材料中(图1a、1b),由于原料钛粉尺寸(0~45 μm)与纤维长度(约30 μm)相近,导致这种网状结构并不明显。TiB短纤维可被认为近均匀的分布在钛基体中。

图1 腐蚀后SmallTi-7.5TiB和LargeTi-7.5TiB复合材料的显微形貌
图2为钛基复合材料及纯钛的拉伸应力-应变曲线。表1为钛基复合材料的力学性能测试结果(多个试样的平均值)。随着TiB纤维体积分数的增加,复合材料的杨氏模量(E)、屈服强度(Rp0.2)及抗拉强度(Rm)均随之上升,而伸长率(A)随之下降。对比近均匀(SmallTi-xTiB)与非均匀(LargeTi-xTiB)钛基复合材料,在TiB体积分数相同的情况下,前者的屈服强度和抗拉强度稍高于后者,但前者的伸长率明显高于后者;且随着TiB体积分数的增加,二者伸长率的差距增大。当TiB纤维体积分数从5%增加到10%时,二者伸长率的差异由0.8%提升到8.6%。

图2 钛基复合材料及纯钛的拉伸应力-应变曲线

表1 制备的钛基复合材料及纯钛的力学性能测试结果
2.2 模拟结果
通过有限元模拟进一步研究TiB纤维的分布对钛基复合材料拉伸性能的影响。基于上述实验数据构建代表性体积单元,并进行了大量的简化与假设。模型设置如下:① 代表性体积单元为边长70 μm的正方体(其体积接近直径为75~106 μm球形粉末的平均体积);② TiB纤维在钛基体中均沿拉伸的轴线方向分布(若纤维取向采用随机分布,则在纤维数量不多的情况下,纤维在空间上各个方向的整体取向无法均匀一致,使得2个模型的力学性能难以相互比较);③ TiB纤维外接圆直径为2 μm(且假定纤维为正六边形)及长度为15 μm(因纤维取向由实验中的随机分布改为模拟中的同向分布,本处参照文献报道的2种纤维取向的强化效果差异,相应缩短其长度[18]);④ 对于非均匀分布的TiB纤维,其在代表性体积单元内分布在距离单元表面20 μm内的区域,即单元中心50 μm×50 μm×50 μm的区域中仅有钛基体组织(参考图1d中TiB在网状结构中的分布并做近似处理);⑤ 实验中SmallTi-xTiB复合材料中TiB纤维为近均匀分布,但在对应模型中对TiB纤维采用均匀分布;⑥ 2个模型中钛基体的弹塑性参数均采用上述实验中SmallTi的结果(消除2个模型之间基体差异对模拟结果的影响);⑦ 任意2根TiB纤维之间最近的距离不小于1 μm(满足网格划分与计算要求);⑧ 复合材料弹塑性行为的求解基于TiB纤维弹性性质和基体弹塑性性质的简单耦合,仅计算应变为0%~1%的行为(由于模型忽略了塑性变形中纤维/基体界面开裂及纤维断裂等复杂情形,塑性应变大时计算的失真度大)。TiB纤维均匀分布和非均匀分布的Ti-7.5vol%TiB复合材料的代表性体积单元如图3所示。代表性体积单元中心区域(50 μm×50 μm×50 μm)全部为基体组织。

图3 Ti-7.5vol%TiB的代表性体积单元(70 μm×70 μm×70 μm,显示纤维和单元轮廓)
图4为TiB(7.5 vol%)纤维均匀与非均匀分布的钛基复合材料模型的模拟拉伸应力-应变曲线。在1%的应变内,2种模型的杨氏模量和抗拉强度基本相当,其中抗拉强度的差别在2 MPa以内。2种模型的杨氏模量均约为133 GPa,屈服强度均约为521 MPa。模拟结果与上述实验结果具有一定的差异,这主要来自于模型的简化与假设。但是,均匀与非均匀2个模型之间可以进行对比分析。
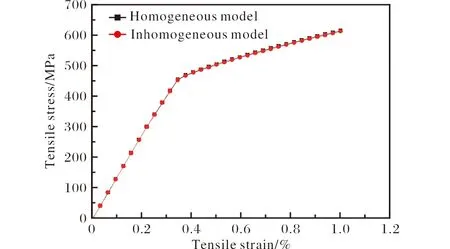
图4 TiB(7.5 vol%)纤维均匀与非均匀分布的钛基复合材料模拟拉伸应力-应变曲线
图5给出了当应变为0.4%时(开始进入塑性变形阶段),2种模型内部的米塞斯应力和最大主应力分布。从图5a和5b中可以看出,在纤维两端附近基体中的米塞斯应力较高,而在纤维侧面附近基体中的米塞斯应力较低。在纤维均匀分布的模型中,基体中的米塞斯应力在空间整体分布也更均匀;在非均匀模型中,存在着米塞斯应力较高或较低的大块连续区域。图5c和5d主要展示了复合材料的最大主应力分布。可以看出,在基体中,最大主应力较大的区域一般在纤维两端附近,且非均匀模型中基体的最大主应力>400 MPa的区域尺寸多于均匀模型。由于基体的单元格中最大主应力的方向与拉伸轴方向一致,因此这表明在非均匀模型中纤维/基体界面附近区域的法向张应力的聚集程度较均匀模型大。在TiB纤维中,纤维的中部是应力最集中的位置。而且,TiB纤维分布的均匀性影响纤维之间应力的分布。相比于均匀模型,在非均匀模型中不同位置的纤维之间,最大主应力的分布存在着明显差异。

图5 0.4%应变下均匀模型和非均匀模型中米塞斯应力和最大主应力分布
表2给出了均匀模型和非均匀模型Ti基体的米塞斯应力和TiB纤维的最大主应力的平均值和最大值。从表2中可以看出,2个模型基体的平均米塞斯应力相当,仅在最大米塞斯应力上稍有差异。在均匀模型中,TiB纤维最大主应力的平均值(1751 MPa)稍高于非均匀模型(1740 MPa),但是前者中TiB纤维最大主应力的峰值(2575 MPa)明显低于非均匀模型(2878 MPa)。这是由于在非均匀模型中不同位置的TiB纤维受力不均,因而出现一些处于高应力状态的纤维。以2200 MPa应力为例,在均匀模型中某个单元格的最大主应力高于此值的纤维的数量为78根,而在非均匀模型中纤维数量达到了164根(代表性体积单元中纤维的总数为660根)。

表2 均匀模型和非均匀模型在0.4%应变下的应力统计(MPa)
3 讨 论
采用细钛粉制备的SmallTi-xTiB复合材料的氧含量稍高于采用粗钛粉制备的LargeTi-xTiB复合材料(氧含量高出约0.04%)。根据理论公式Δσ=0.02Gc1/2(其中G是Ti基体剪切模量,c是氧原子占比)[19],氧含量差异导致SmallTi-xTiB复合材料的强度比LargeTi-xTiB复合材料高出约7 MPa。拉伸实验结果表明,在TiB体积分数相同时,纤维近均匀分布的SmallTi-xTiB复合材料的屈服强度和最大强度比纤维非均匀分布的LargeTi-xTiB复合材料稍高(不超过20 MPa)。考虑到2种复合材料其他方面的组织接近,因此可推断出TiB纤维分布的均匀性对钛基复合材料强度的影响很小。模拟结果证实了纤维均匀分布与非均匀分布的2类复合材料的杨氏模量和屈服强度基本一致。
实验表明,纤维非均匀分布的钛基复合材料的拉伸塑性明显低于纤维近均匀分布的钛基复合材料,尤其是纤维体积分数越高这种差异越明显。当TiB体积分数为10 vol%时,近均匀复合材料的伸长率为14.8%,明显高于非均匀复合材料的伸长率(6.2%)。复合材料沿纤维轴向受拉时,部分载荷通过剪切机制从基体转移到纤维上,在纤维长度方向的中间位置出现应力集中,而在纤维两端的基体处,出现界面法向张应力的集中[20, 21]。本研究中的模拟结果证实了这一受力状况。由于纤维与基体之间存在上述的作用机理,当纤维的两端靠近时,可造成基体中应力集中区域的叠加。纤维分布不均时,基体中局部应力集中区域叠加的程度加剧。此外,由于纤维分布不均导致不同区域纤维数量不一致,在纤维少的局部区域,单根纤维承载的载荷增加,纤维内部的应力升高。
基体的米塞斯应力分布不均代表着基体的协调变形能力更差,基体在高应变下更容易发生变形失稳而产生裂纹的形核与扩展。基体中出现最大主应力集中表明局部变形加剧,且由于最大主应力的方向与纤维的轴向一致,使得纤维端面和基体的结合界面在法向张应力导致的张应变下更易被撕裂,形成复合材料内部的裂纹源。此外,单根纤维内部局部的最大主应力(轴向应力)的过高造成纤维本身断裂的风险加剧[21]。随着TiB体积分数的增大,局部聚集的TiB纤维更多,相当于纤维分布的不均匀性加剧。这些因素解释了实验中纤维不均匀分布的LargeTi-xTiB复合材料的拉伸塑性比纤维近均匀分布的SmallTi-xTiB复合材料更低,而且随着TiB纤维体积分数的增加,二者塑性的差距加大。当TiB纤维体积分数从5%增加到10%时,二者伸长率的差异由0.8%提升到8.6%。由此可以推断,当TiB纤维体积分数在10%以上时,二者塑性的差别可能更大;而TiB纤维体积分数在5%以下时,二者塑性的差别较小。
以上初步研究了TiB纤维分布的均匀性对纯钛基复合材料拉伸性能的影响。由于TiB纤维非均匀分布带来的上述3个影响要素(基体中米塞斯应力分布均匀性降低,纤维/基体界面附近的法向张应力增加,以及TiB纤维上的最大主应力的峰值升高)对复合材料的塑性均不利,因此可以推断TiB纤维的非均匀分布对钛基复合材料的塑性均不利。当然,由于本实验未深入研究3个影响要素之间的主导关系,且当基体类型发生变化时材料的力学行为会发生改变,因此TiB纤维的非均匀分布对其他钛基复合材料拉伸塑性的影响程度可能发生变化。可通过实验进一步研究TiB纤维增强钛基复合材料中复合材料拉伸断裂失效的主导机理,以更好地指导非连续纤维增强钛基复合材料的设计。
4 结 论
(1) TiB纤维分布的均匀性对钛基复合材料的抗拉伸强度和杨氏模量影响均很小。
(2) TiB纤维非均匀分布钛基复合材料的拉伸塑性低于近均匀钛基复合材料;且随着纤维体积分数增加,二者塑性的差距增大。
(3) 相比TiB纤维均匀分布的钛基复合材料,非均匀钛基复合材料基体中的米塞斯应力分布更不均,纤维/基体界面附近的法向张应力加剧,TiB纤维上的最大主应力的峰值更高,钛基复合材料中裂纹形成的风险更高。
