基于地震观测记录的场地竖向非线性性质
2021-07-14龙晓鸿
苗 雨, 施 洋, 张 昊, 龙晓鸿
(华中科技大学土木与水利工程学院, 武汉 430074)
许多实验结果[1-3]与基于地震观测记录的研究结果[4-7]表明,场地在强地震作用下会进入显著的非线性阶段,而地震灾害作为一种破坏性强且难以准确预测的自然灾害,在工程领域及相关研究领域都受到广泛关注,因此场地非线性性质的准确评估尤为重要. 同时这也是许多相关研究以及实际应用的基础[8-14]. 场地的非线性性质针对地震动的不同分量分为水平与竖向非线性性质,目前的研究主要集中于水平非线性性质,许多国家的抗震设计规范对场地竖向非线性性质的考虑也仅限于某些重要建筑,对于一般建筑,对场地竖向非线性性质的考虑往往被忽略或是简化. 然而许多震害调查结果[15]显示,不仅是重要建筑,许多一般建筑的破坏也与场地竖向非线性性质直接相关. 然而到目前为止,场地竖向非线性性质的相关研究首先是数量较少;此外由于竖向地震动记录的数目相比水平地震动较稀缺,导致选取的数据离散性较大,同时由于研究方法的不同,彼此得出的结论之间可能会有一定区别. 因此,目前对场地竖向非线性性质的认识相较而言仍比较有限,有必要对其进行进一步的研究.
场地非线性性质的研究大体上可分为3个部分:非线性阈值的判别、非线性程度的评估以及强震之后场地性质的恢复过程. 场地的非线性阈值被定义为介于场地线性阶段与非线性阶段的临界状态,多通过应变[1-4]以及地面峰值加速度(peak ground acceleration,PGA)[7,16-18]表征. 目前对场地非线性阈值的研究多集中于场地的水平非线性阈值,对场地竖向非线性阈值的研究仍十分有限[19],且场地的非线性阈值本身具有较高的离散性,因此需要更多的相关研究提高数据的容量. 场地的剪切模量与压缩模量是确定场地性质的重要物理量,当场地处于非线性阶段时,模量衰减曲线被用来描述场地的模量随应变变化的关系[1-4,20]. 如前所述,目前对场地模量曲线的研究多集中于剪切模量曲线,与剪切模量不同,由于水的不可压缩性,饱和度对压缩模量有显著影响[19-20],特别是对于实际场地,需合理考虑地下水的影响. Shi等[19]基于日本基岩强震观测网(Kiban-Kyoshin strong motion observation network,KiK-net)地震观测记录,提出考虑地下水影响的场地压缩模量曲线模型,但是由于其研究中使场地产生较高应变反应的强震记录较少,故其模型的有效性有必要通过更多的补充研究进行进一步的验证. 许多学者通过研究发现场地在强震之后其物理力学性质存在向震前水平趋近的恢复过程,整体上这种恢复过程可以用对数函数描述[21-22]. 恢复过程的时间跨度具有高度的离散性,跨度能从数秒至数年甚至不完全恢复直至当前记录时间[23-27]. 目前强震之后场地竖向性质恢复过程的相关研究同样比较不足,无论是强震对场地竖向性质的影响程度还是之后的恢复时间都需进一步研究.
本研究分为以下几个部分:首先从日本KiK-net强震观测台网中选择合适的地震台站与记录;然后通过地震干涉测量法以及土动力参数法从地震记录中提取场地的压缩模量以及应变,时频分析技术被应用到地震干涉测量法中以增加强震记录的数目;再使用目前已有的考虑地下水影响的场地压缩模量曲线模型估计所选台站的压缩模量曲线,基于所得模量曲线结果对模型的有效性进行验证并开展包括非线性阈值在内的相关研究;最后对强震之后场地竖向性质的恢复过程进行相关研究.
1 研究数据
KiK-net是日本全国性的强震观测台网,由日本防灾科学技术研究所(National Research Institute for Earth Science and Disaster Resilience,NIED)于1995年神户地震之后修建. 整个台网由约700个均布于日本全国境内的地震台站构成. 每个台站包含1个钻孔以及1组分别布置在钻孔底部和地表的三向地震仪. 大部分台站的钻孔深度分布在100~200 m,少部分能达到数百米至数千米[28]. 三向地震仪的采样频率初始设定为200 Hz,约在2007年变更为100 Hz. 除此之外,部分台站约在2013年经历过一次台站调整,虽然采样频率保持不变,但场地信息可能会受到影响. 台站对应场地的详细地质地理信息以及钻孔剖面可在NIED官网查询得到,网址为:https:∥doi.org/10.17598/NIED.0004.
本研究所用地震记录截止日期为2019年10月. 由于2007年和2013年台站调整可能会导致场地信息的变化,故本研究中所选台站仅采用记录时间在2次台站调整之间的记录. 本研究中确定的台站筛选条件有以下几点:1)为保证地震记录的充足性,所选台站需至少有400条地震记录. 2)为保证能在一定程度上观测到场地的非线性性质,所选台站需至少有2条地面峰值加速度水平分量(horizontal component of peak ground acceleration,PHA)大于100 cm/s2的地震记录. 3)为消除台站钻孔深度的影响,所选台站的钻孔深度应在100~120 m. 最终有10个台站被选择为本研究的样本台站,这些台站的相关信息见表1. 图1显示本研究所选地震台站以及对应地震记录的相关信息. 如图1(a)所示,矩震级(MW)不小于8级的地震共有3个,其中2011年东日本大地震的震源震级最大且最靠近所选台站,表明本研究所选场地的最大非线性状态主要受该地震影响. 图1(b)描述了本研究所用地震记录对应震源的震级以及震源深度,可以发现绝大部分的震源深度均小于100 km,表明大部分地震为浅源或中源地震. 图1(c)(d)分别描述了本研究所用地震记录的PGA与震中距的关系,其中PVA为地震记录的地面峰值加速度竖向分量(vertical component of peak ground acceleration,PVA),结合图1(a)可以看出本研究所用地震记录对应震源在空间分布上具有广泛性.
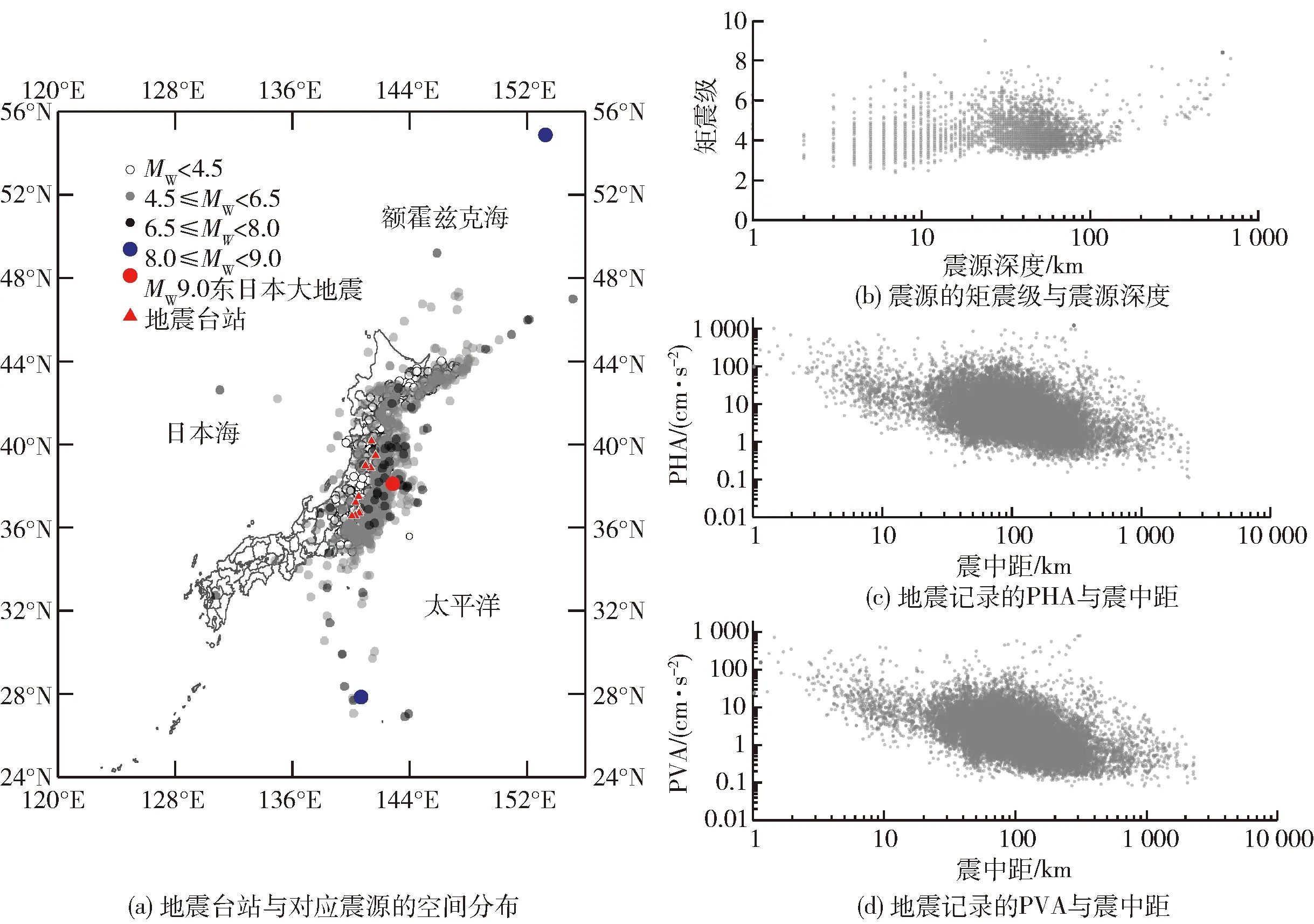
图1 本研究所选地震台站及对应地震记录的相关信息Fig.1 Related information of the selected seismic stations and corresponding records
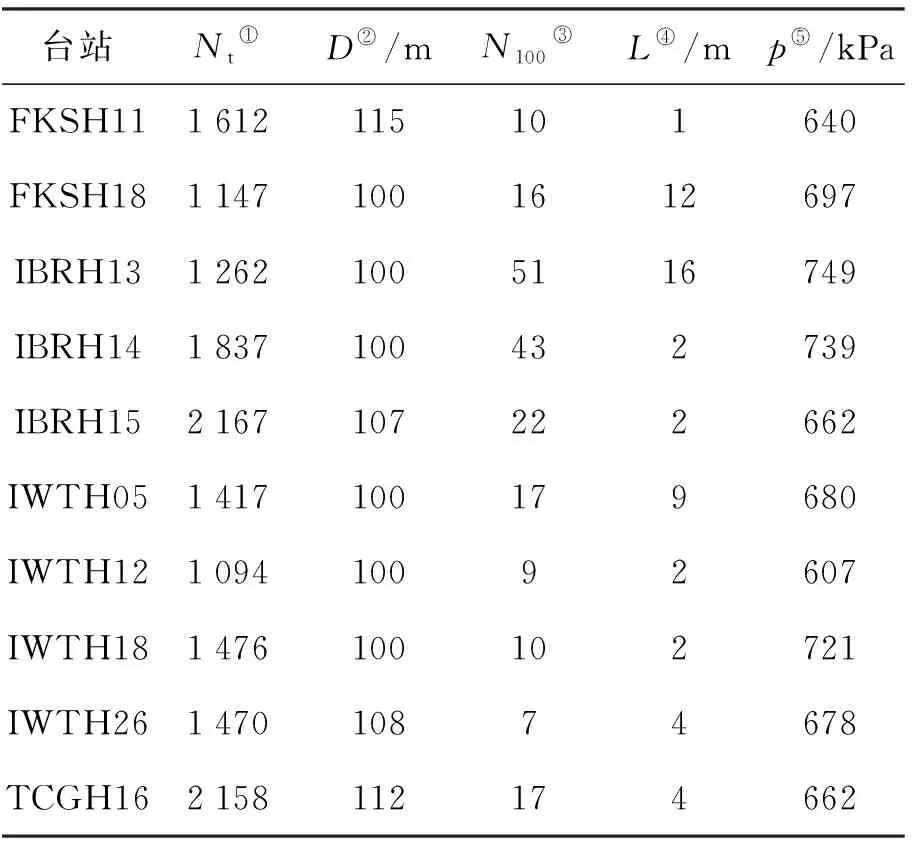
表1 所选地震台站的相关信息
2 基于地震观测记录估计场地压缩模量曲线
2.1 提取场地压缩模量
基于一维波动传播理论[20],场地模量的计算公式为
(1)
式中:G和M分别为场地剪切模量与压缩模量;VS和VP分别为场地剪切波速与压缩波速;ρ代表场地的厚度加权平均密度[29].由于ρ为与时间无关的常数,因此式(1)可转化为
(2)
式中:G0和M0分别为小应变下场地剪切模量与压缩模量,也称为场地模量最大值;VS0和VP0分别为小应变下场地剪切波速与压缩波速.通过土动力参数法,每条地震记录均可提取出对应的等效应变,本研究将对应应变不大于所属台站全记录对应应变10%分位数的记录视为该记录所属台站的小应变记录,亦即对应应变最小的10%的地震记录.所有小应变记录估计结果的平均值被定义为对应场地小应变下的性质,如台站中所有小应变记录的压缩模量估计值的平均值即为该台站所在场地的M0.
本研究选择地震干涉测量法作为提取场地地震波速的方法.地震干涉测量法在地震工程领域应用广泛[30-32],其原理是将钻孔井下地震仪视为虚拟震源,通过估计场地格林函数进而估计地震波从虚拟震源至地表地震仪的走时,钻孔深度除以走时即为场地等效地震波速.基于格林函数形式的不同,地震干涉测量法也有对应的区分.由于解卷积函数形式的格林函数能消除入射波场的影响[31],本研究选择基于解卷积函数的地震干涉测量法进行场地地震波速的提取.解卷积函数形式的格林函数为
(3)
式中:ub(ω)与us(ω)分别为钻孔井下地震仪与地表地震仪地震记录的傅里叶变换;*为共轭符号;α为用来提高计算稳定性的正则常数,本研究设定为井下地震仪地震记录功率谱频率平均值的1%[31].
实际操作过程中,首先需对所选地震记录进行滤波. 考虑剪切波与压缩波各自的能量频谱分布,本研究对地震记录水平分量(东西方向(east-west,EW)与南北方向(north-south,NS))的滤波范围为1~13 Hz[19,31],对竖向分量(up-down,UD)的滤波范围为1~30 Hz[20,33]. 通过滤波之后的地震记录计算得到对应的解卷积函数之后,将其通过傅里叶逆变换转换到时域,地震记录对应走时即为时域内解卷积函数在参考走时附近的峰值时间(场地参考走时为基于场地地震波速剖面的估计值). 对于地震记录的竖向分量,其估计结果直接对应场地的压缩波速. 然而对于地震记录的水平分量,由于横波分裂的现象,场地的剪切波速会随方位角的变化而发生变化,直观体现在场地EW与NS方向对应的结果具有显著的非一致性. 针对此现象,本研究首先将EW与NS方向的地震记录分量以10°为间隔分别从0°到180°方位角进行合成,得到18组记录,进而得到场地各方位角对应的剪切波速. 依据目前已有的相关研究结果[31],本研究使用各向同性项即场地各方位角对应的剪切波速的平均值作为场地剪切波速的代表值.
除此之外,为增加可用强震记录数目,本研究将时频分析引入地震干涉测量法. 如图2所示,即针对PHA大于100 cm/s2的地震记录,通过施加窗长10.24 s、步长1.00 s的移动时间窗将地震记录细分为若干子记录,针对每组子记录分别使用上述方法估计其对应地震波速. 图2(b)(c)分别表示样本记录EW与UD方向不同时间窗时域内的解卷积函数,竖直虚线表示解卷积函数对应的走时,可以发现不同时间窗对应子记录的结果的性质与实际规律基本一致,即走时先增大后恢复减小,表现出强震记录过程中场地性质随时间的变化,体现该方法的合理性.
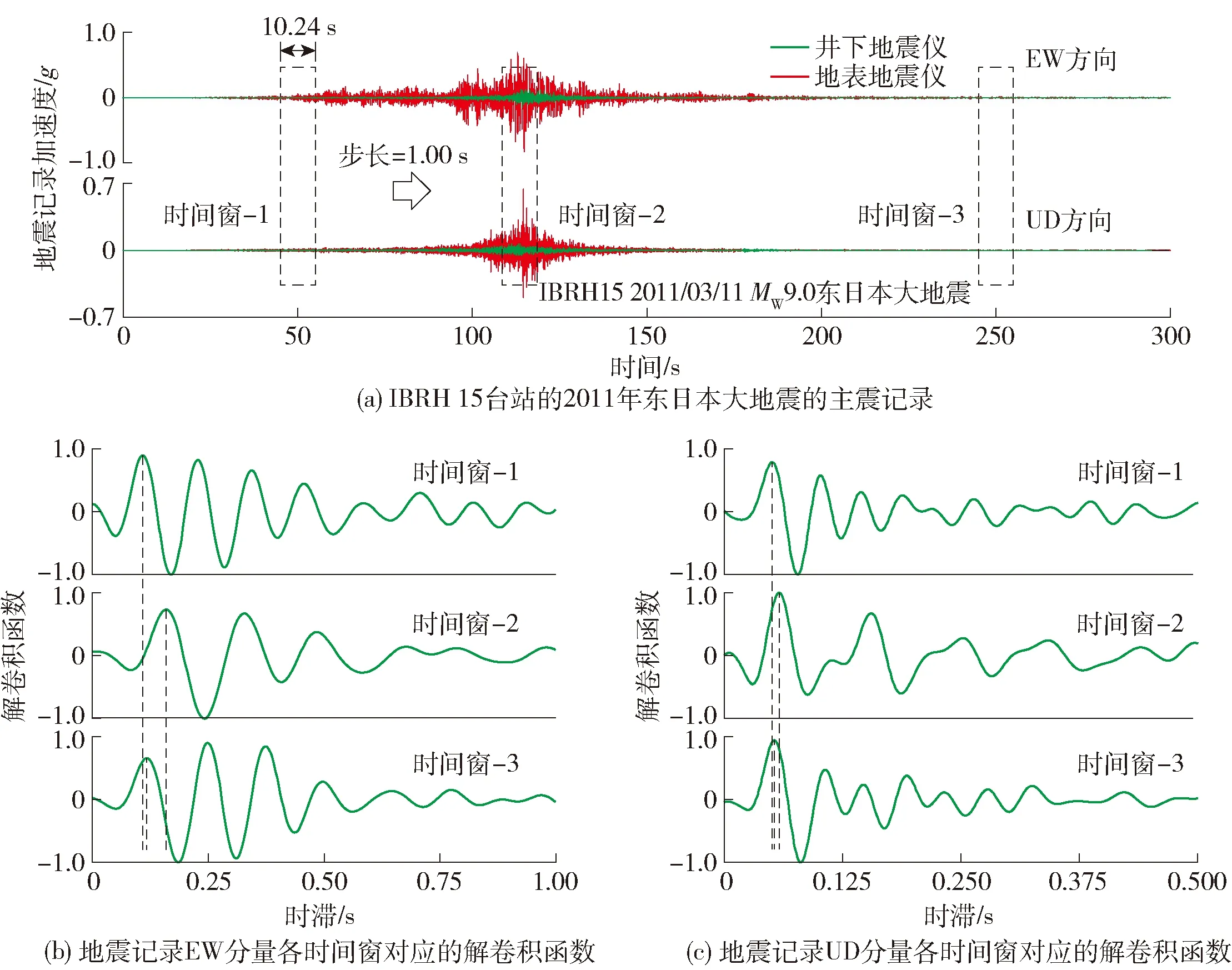
图2 结合时频分析技术的地震干涉测量法的应用实测Fig.2 Application of seismic interferometry combined with the time frequency analysis
2.2 提取场地应变
基于波动传播理论,场地应变与场地振动速度和场地地震波速的关系[34]为
(4)
式中:γ为场地切应变;VH与VS分别为场地水平振动速度与剪切波速的代表值.
依据式(4)中场地水平振动速度与剪切波速代表值形式的不同,场地应变的估计方法也有不同区分,本研究与Chandra等[4-5]和Wang等[7]一致,将VH定义为地表与井下地震记录速度时程平均的绝对值的最大值,将VS定义为按2.1节所示方法估计得到的场地剪切波速代表值.
2.3 场地压缩模量曲线估计结果
从地震记录提取出场地压缩模量及应变之后,通过场地压缩模量(比)曲线模型即可估计得到对应压缩模量(比)曲线.本研究选取Shi等[19]提出的模型进行场地压缩模量(比)曲线的估计,即
(5)
式中kM与bM均为拟合参数.值得一提的是,式(5)的原本形式为压缩模量与正应变之间的关系[19],由于场地切应变与对应正应变之间存在对数线性的关系[19],故场地压缩模量与切应变之间的关系可用同样的模型描述.本研究使用压缩模量与切应变的形式旨在使场地竖向非线性性质与水平非线性性质的对比更加直观与明显.本研究中剪切模量曲线模型选择双参数双曲线模型[2,35],即
(6)
式中:kG与bG均为拟合参数.该模型应用广泛且模型参数数目与本研究中所选压缩模量曲线模型一致.
所选地震台站对应场地压缩模量曲线与剪切模量曲线的估计结果如图3所示,对应拟合参数及拟合精度见表2、3.首先可以发现时频分析技术能有效增加强震记录的数目,具体体现在应变大于10-4的地震记录的数目显著增加,进而使地下水对场地压缩模量的影响在结果上更加直观,从观测角度验证了本研究所选模型理论的合理性[19-20].此外,压缩模量曲线的估计结果与基于地震记录的观测值基本一致,从数学上验证了该模型的拟合精度.总体而言,本研究的结果进一步证明了该模型的有效性.对比图3所示各场地的压缩模量曲线与对应剪切模量曲线,整体上场地压缩模量的衰减程度与速度小于对应剪切模量,特别是对于应变较大(大于10-4)的情况,场地剪切模量的衰减速度显著增加而压缩模量的衰减速度却逐渐减缓且呈现出较明显的衰减下限,原因在于地下水的不可压缩性对场地竖向非线性性质的抑制作用,而这也与基于理论[20]以及地震观测[19]的结果一致.

图3 所选地震台站对应场地压缩模量曲线与剪切模量曲线的估计结果Fig.3 Estimates of the constrained and shear modulus degradation curves with the measured values of the selected stations

表2 所选地震台站对应拟合参数及拟合精度(剪切模量)
3 场地竖向非线性阈值及相关讨论
场地非线性阈值的确定方法主要分为两部分:首先是能合理评估场地非线性程度的指标,然后是针对选定的指标判定场地是否进入非线性阶段的标准. 目前评估场地非线性程度应用较广泛的指标主要有场地模量[7]、基本频率[17-18]等. 针对不同的指标,判定场地是否进入非线性阶段的标准也各有不同,本研究选取压缩模量作为判定指标. 由于场地的非线性阈值本身具有较高的离散性,因此对非线性阈值的研究主要在于确定其大体分布范围,除此之外,由于强震记录数目限制以及地下水的影响,竖向非线性阈值的离散性可能会更高,故通过压缩模量判定场地到达非线性阶段的标准在各种不同的研究中也有一定区别. 由于目前针对场地水平非线性阈值的研究较为充足,对场地水平非线性阈值分布范围的认知较为统一(水平非线性阈值应变大致分布范围为10-6~5×10-5)[1-2,4,7],因此本研究分别以场地模量衰减至最大值的97%与99%为标准,分别估计各自对应的水平非线性阈值并以其结果作为参照与目前已有结论对比进而确定合适的非线性阈值判定标准,结果如图4所示. 其中,偏右与偏左的阴影区域分别表示以场地模量衰减至最大值的97%与99%为标准的非线性阈值范围.

表3 所选地震台站对应拟合参数及拟合精度(压缩模量)

图4 所选地震台站对应场地的非线性阈值范围Fig.4 Ranges of the nonlinear thresholds of the selected sites
由图4所示,首先可以发现,由于地下水的影响,场地压缩模量曲线整体上而言更加平缓,体现在非线性阈值范围上的影响就是相比水平非线性阈值,其离散性更高,范围更大. 具体而言,以场地模量衰减至最大值的99%为标准,场地水平非线性阈值范围大致为10-6~5×10-5,对应竖向非线性阈值范围大致为5×10-7~10-4;以场地模量衰减至最大值的97%为标准,场地水平非线性阈值范围大致为5×10-6~10-4,对应竖向非线性阈值范围大致为10-6~5×10-4. 另一方面,整体上而言场地竖向非线性阈值仍然大于对应水平非线性阈值,这同样归因于地下水对竖向非线性性质的抑制作用. 由于以场地模量衰减至最大值的99%为标准确定的水平非线性阈值范围与目前已有结果较一致[7,18],故本研究对场地竖向非线性阈值范围的估计结果同样以此标准为主,综合考量下确定为10-6~10-4.
由于地下水的不可压缩性,场地压缩模量曲线具有衰减下限,且其主要受地下水位以及地下水与非饱和状态场地的压缩模量比控制[19]. 由于场地模量受到围压的影响十分显著[36-37],故本研究选取围压以及地下水位为研究对象,分别对这2种因素与压缩模量曲线衰减下限的经验关系进行调查分析. 由于样本容量的限制,本研究难以严格地控制变量,故这部分研究也主要以整体上的定性分析为主. 场地的地下水位可通过对应钻孔剖面估计[38],等效围压估计为
(7)
式中:ρi和Hi分别为台站钻孔第i层的密度以及厚度;ρw为地下水的密度,本研究设定为1.0 g/cm3;Hw为台站钻孔地下水位以下的厚度;g为重力加速度,本研究设定为9.8 m/s2.ρi由台站钻孔剖面结合式确定[29],且

(8)
结果见表1. 由图5(a)可发现,场地压缩模量曲线衰减下限与围压整体上呈线性负相关的关系. 从物理原理上解释,围压增加会增大场地非饱和状态下的压缩模量,进而减小地下水的压缩性在场地整体压缩模量中的影响占比,最终降低场地压缩模量曲线的衰减下限. 图5(b)描述了压缩模量曲线衰减下限与地下水位的关系,可以发现与围压的影响类似,压缩模量衰减下限与地下水位之间同样在整体上存在负相关性. 其原因可解释为,地下水位的降低会直接减弱地下水的压缩性在场地整体压缩模量中的影响占比,进而降低场地压缩模量曲线的衰减下限.

图5 所选地震台站对应场地的压缩模量比衰减下限与等效围压以及地下水位的关系Fig.5 Relationships between the confining pressure and the low limit of constrained modulus degradation curve and between the GWL and the low limit of constrained modulus degradation curve
4 场地竖向性质的恢复过程
本研究还进一步调查了场地性质受强震影响的程度及之后的恢复过程. 由式(1)可知,场地模量的变化可直接由对应地震波速评估,故本部分研究以地震波速作为场地性质的代表. 由图1(a)可知,2011年东日本大地震的震源在矩震级不小于8级的3个震源中震级最大(Mw=9)且最靠近所选台站,表明本研究所选场地的最大非线性状态主要受该地震影响. 综合而言,本部分研究以场地地震波速为场地性质的代表,研究其受2011年东日本大地震影响的程度及之后的恢复过程.
为排除其他强震的干扰,10个地震台站被进一步筛选最终得到满足要求的6个样本台站. 图6给出这些台站对应场地的结果,其中地震波速参考值被定义为2011年东日本大地震之前场地地震波速的平均值,第0天为2011年东日本大地震主震发生时间,水平虚线分别表示场地压缩波速(上)与剪切波速(下)的最大下降幅度. 主震后地震波速的平均时间区间为[1, 10, 30, 60, 90, 180,360,540,…,3 240,3 420]d. 由图6可以发现,首先压缩波速受强震影响的程度明显小于剪切波速,针对2011年东日本大地震而言,本研究中样本台站压缩波速的最大下降幅度为5%~20%,剪切波速的最大下降幅度为20%~35%,两者最大下降幅度的差异为10%~15%,一定程度上反映了地下水对场地竖向非线性性质的抑制程度. 除此之外,场地压缩波速恢复过程与剪切波速的恢复过程之间整体上并无明显规律性的区别,除FKSH18、IBRH13和IBRH14台站之外,其余台站对应场地的地震波速均已恢复至震前水平,恢复时间基本为1 000~2 000 d. 由于FKSH 18、IBRH 13台站约在2013年受到台站调整的影响,故这2个台站的地震记录仅使用到2013年台站调整为止即东日本大地震震后约700 d,相比其他台站,这2个台站地震波速恢复不充分的原因很可能是长期恢复过程还未结束,地震波速将继续恢复直到震前水平为止. 与之相比,IBRH 14台站恢复不充分的原因则很可能是主震对场地已造成永久性的破坏,场地性质不再会恢复到震前水平[7].
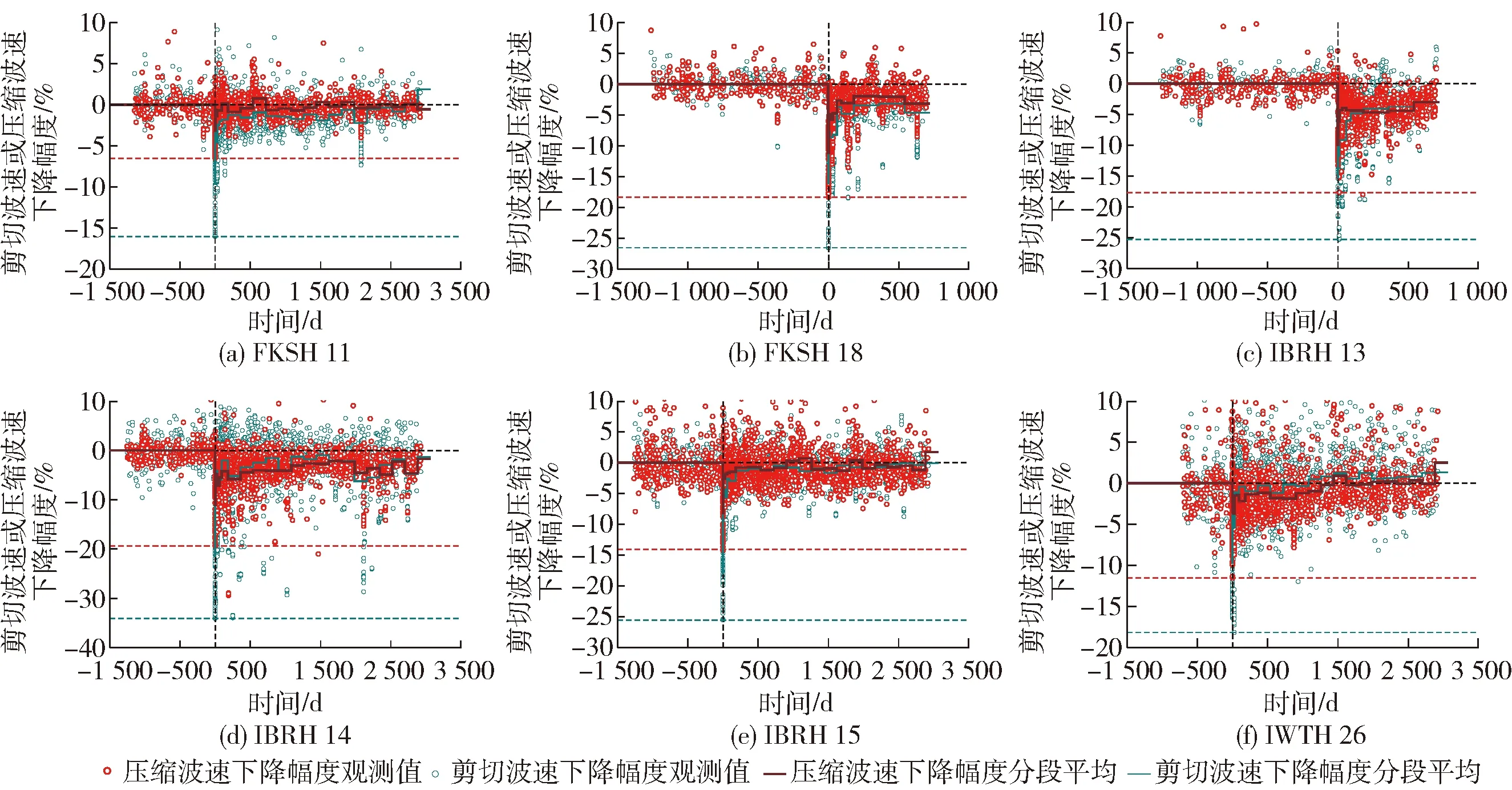
图6 所选地震台站对应场地的地震波速受2011年东日本大地震影响的降低程度及之后的恢复过程Fig.6 Plunges and recovery processes of seismic velocities for the selected stations after the Tohoku earthquake
5 结论
本研究基于日本KiK-net强震观测记录,探究了场地的竖向非线性性质,包括对目前场地原位压缩模量曲线模型的验证、场地竖向非线性阈值范围的确定、强震之后场地竖向性质的恢复过程等. 主要结论如下:
1) 通过引入时频分析技术,有效增加了强震记录的数目,估计了样本场地的原位压缩模量曲线并基于此进一步验证了目前场地原位压缩模量曲线模型的有效性. 整体上场地压缩模量的衰减程度与速度小于对应剪切模量,特别是对于应变较大(大于10-4)的情况,场地剪切模量的衰减速度显著增加而压缩模量的衰减速度却逐渐减缓且呈现出较明显的衰减下限,原因在于地下水的不可压缩性对场地竖向非线性性质的抑制作用.
2) 场地竖向非线性阈值应变的范围为10-6~10-4,相比水平非线性阈值,其离散性更高,范围更大. 由于地下水的影响,场地竖向非线性阈值大于对应水平非线性阈值.
3) 场地原位压缩模量曲线衰减下限与围压以及地下水位均呈负相关关系,原因可归纳为围压与地下水位的增加会减弱地下水的压缩性在场地整体压缩模量中的影响占比,进而降低场地压缩模量曲线的衰减下限.
4) 本研究中样本台站在2011年东日本大地震影响下,压缩波速与剪切波速的最大下降幅度分别为5%~20%与20%~35%,两者最大下降幅度的差异为10%~15%,一定程度上反映了地下水对场地竖向非线性性质的抑制程度. 此外,场地压缩波速与剪切波速的恢复过程整体上并无明显规律性的区别.
5) 需要注意的是,本文的研究结论从性质上大体可分为两部分. ① 定性的规律性的结论,如场地压缩模量曲线的衰减规律、压缩模量曲线与剪切模量曲线的定性对比关系、围压与地下水位对压缩模量衰减下限的影响规律等,这部分结论因为有相关理论作为依托,所以一定程度上可以认为具有普适性;② 偏定量的结论,如场地竖向非线性阈值的分布范围、场地地震波速受强震影响的衰减幅度等,这部分结论可能由于实际场地构成与地震动的复杂性而导致结果具有一定程度的区域相关性,在实际使用的时候需要注意将目标场地与本文的样本场地进行适当的对比.
致谢
感谢国家自然科学基金(51778260,51978304,51978306)长久以来的资助,感谢日本防灾科学技术研究所(National Research Institute for Earth Science and Disaster Resilience)提供的强震动数据.
