基于A*算法的深部地下空间火灾疏散路径动态规划

黄 昕， 靳 健， 林作忠， 车轮飞， 刘 俊

(1.同济大学地下建筑与工程系， 上海 200092； 2.中铁第四勘察设计院集团有限公司， 武汉 430063)

随着我国经济快速发展，地下空间利用规模越来越大，并逐渐向深部扩展，三维空间开发已是发展的必然. 相比浅部地下空间，深部地下空间具有建筑规模大、设备复杂、通道单一、与外界交互差等特征，这使得深地空间内部一旦发生火灾其救援难度和人群疏散盲目程度更大. 并且由于火灾发生的突发性、多变性和烟毒性特点，传统的静态火警疏散图在数据含量、空间表现上的不足日益明显，难以准确、动态地反映火灾发生时内部空间的通达性和有效逃生空间，无法正确判断失火点相关的局部区域特征[1]. 传统的疏散指示系统无法感知动态数据，无法实时根据现场环境改变调整疏散指示方向，因此，在火灾发生时对疏散路径实时动态地优化至关重要[2].

在静态路径规划方法上，贾进章等[3]提出基于遗传- 蚁群算法求解火灾时期人员疏散路径，缩短路径生成时间，提高逃生效率. 许胜[4]依托商场和地铁的综合性地下建筑，将应用Pathfinder软件不考虑疏散指示装置的场景和利用Dijkstra算法改进疏散指示装置的场景进行对比，实现了合理规划人员疏散路径. 李俊[5]提出了社会力改进模型，在复杂环境中能有效绕过障碍物，使人群疏散仿真更加真实. 王培良等[6]建立了以六边形元胞为基础的栅格地图，利用蚁群元胞优化模型进行疏散路径规划，有效地避免陷入局部最优解. 在路径动态规划方法上，刘恒旭[7]以地铁车站为依托，结合火灾动态数据，改进蚁群算法参数及策略选择，寻求最佳疏散策略. Choi等[8]利用火灾动力学模拟器提供建筑物内烟气传播的预测数据，结合A*算法寻找最快速的逃生路径并对算法进行改进，以考虑路径中后续节点的安全状态. Wang等[9]建立了基于Pathfinder的高层建筑火灾现场疏散模型，结合疏散行为和烟气扩散速度、温度以及CO体积分数进行分析. Yan等[10]提出了一种基于复用动态信息素的蚁群优化算法，并应用于实时火灾疏散系统中.

上述成果给火灾条件下的疏散路径规划提供了指导，但是针对大尺寸复杂结构，基于火灾情况下温度变化和烟气扩散对逃生疏散路径进行动态规划的研究尚不完善，而这正是疏散更加困难的深地空间人员安全逃生和救援疏散策略制定需要重点解决的难题. 本文在充分对比Pathfinder软件、蚁群算法、A*算法的疏散路径规划效果的基础上，建立了基于A*算法的考虑火灾环境演化的最优疏散路线动态规划方法，可为深地空间救援和疏散路径的实时动态规划提供依据.

1 常用疏散路径规划方法概述

1.1 蚁群算法

蚁群算法最早由Marco Dorigo等提出，用以模拟蚁群在觅食过程通过信息素沟通从而找到通往目的地最优路径的行为[7]. 其中信息素浓度和蚂蚁走过的路径长度密切相关，如果蚂蚁走过的路径越长，其分泌的信息素浓度越低. 随着时间的流逝，信息素将以一定的速度逐渐消失，长时间以后，仅有最短路径上的信息素得以保留，后续蚂蚁也会继续选择信息素浓度高的路径，这种正反馈过程使得蚁群最后将会沿着最短的路径进行移动[7].

蚁群算法的支撑即为状态转移概率

(1)

和信息素函数

τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(2)

的更新. 式中：τij(t)为t时刻(i,j)路径上残留的信息量；ηij(t)为(i,j)之间距离的倒数；α为(i,j)路径上残留信息的重要程度，即信息素启发因子；β为基于距离的启发信息重要程度；P为当前走过路径的集合；ρ为信息素挥发系数；Δτij(t)为在本次循环中路径(i,j)上的信息素增量，与蚂蚁释放的信息素强度Q成正比，与蚂蚁在本次循环中走过的路径长度成反比.

参数α、β、ρ、Q是影响其求解性能和效率的关键因素，其选取方法和选取原则直接影响算法的全局收敛性和求解效率.

1.2 遗传算法

在遗传算法中，路径Pl可以表示为

Pl={P0，P1,P2,…,Pn}

(3)

式中：P0为起点；Pn为终点.

在算法中，将每个路径点表示为1条染色体，路径中的每个阶段(Pi-1,Pi)表示为一个基因. 将路径总长度的倒数作为适应度函数

(4)

式中：xi和yi为第i个路径点的坐标；M为种群规模. 适应度函数值越大，路径性能越好，函数值大的个体是种群中的精英个体. 个体之间能够进行交叉与变异，即路径点的替换. 若替换后适应度函数较变异前更优，则采用变异后的个体，使变异朝着更优的方向进行[3].

基本蚁群算法在求解初始阶段信息素积累不足，为改进这一缺陷，有学者提出了遗传- 蚁群算法[3]，利用了遗传算法前期的全局性、快速性以及蚁群算法在后期的正反馈性，能够始终保持较快的求解速度.

1.3 A*算法

A*算法被认为是Dijkstra算法的扩展，相较于Dijkstra算法，它不仅包括到达下一个节点的距离，还包括到达最终目标节点的预估距离[8]. 当疏散人员当前位置确定时，A*搜索算法很容易定义关于到目标节点距离的启发式信息. A*算法的基本原理为

f(n)=g(n)+h(n)

(5)

式中：f(n)为节点n的求值代价；g(n)为当前节点n0到下一个节点ni的距离；h(n)为从ni到目标节点的最短预估距离，当h(n)始终为0时，A*算法即退化为Dijkstra算法.g(n)和h(n)的计算公式分别为

(6)

(7)

A*算法在路径选取时，优先选择f(n)值最小的节点作为中间节点，算法高效且能够遍历地形图，因此，在路径规划方面广为应用.

1.4 Pathfinder软件

Pathfinder软件是美国Thunderhead Engineering公司开发的基于人员进出和运动的模拟器[11]. 运动环境采用三维三角网格设计，以楼板为基础，地形上的障碍物体现为楼板上的“孔洞”. 其主要针对人群疏散，但也能通过单个人员的疏散模拟结果观察其路径规划. Pathfinder的路径规划的基础即为A*搜索算法，并结合拉索(string pulling)技术[11]，仅在障碍物的转角处进行转向，从而使得疏散路径更加平滑. 其应用较为成熟，但是不能考虑火灾过程中的温度、烟气体积分数的动态变化，其规划出的路线有可能引导人群走进危险区域，造成不必要的生命财产损失. 因此，可以作为不考虑火灾动态发展情况下的路径规划结果参考，验证其他算法的可靠性.

火灾的发展是一个快速过程，真实火灾场景下容许的逃生疏散时间是极其有限的，路径的规划除了要考虑其合理性外，还需考虑规划算法所需的计算时间，故有必要基于以上2个指标对不同的规划方法进行对比分析，确定最优的路径规划方法作为逃生疏散路线动态规划的支撑算法.

2 常用路径规划方法对比

2.1 基于40 m×20 m小尺寸模型

首先建立了一个40 m×20 m的小尺寸模型，其俯视图如图1所示，图中绿色标记为起点位置，红色标记为出口位置.

图1 小尺寸模型俯视图Fig.1 Top view of the small-scale model

分别用蚁群算法、A*算法和Pathfinder软件进行路径规划，其中蚁群算法和A*算法通过Matlab程序自行编制，选取地图中心为起点，左上角出口为目标出口，观察其路径规划结果即计算时间. 路径规划结果如图2所示. 3种方法的路径距离、计算时间如表1所示.

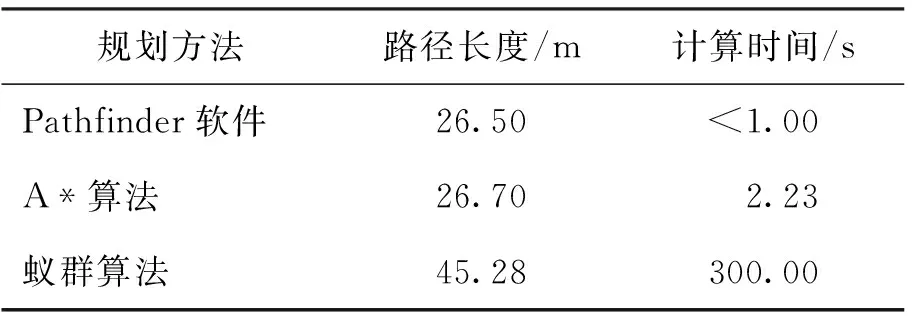
表1 小尺寸模型路径规划方法效果对比

图2 路径规划结果对比Fig.2 Comparison of path planning results

由上述结果得知，基本蚁群算法在45次迭代后陷入了局部最优，因此，规划所得路线极为不规则且规划路径长度及计算时间较长. A*算法和Pathfinder软件的路径距离及计算时间相差不大，但是Pathfinder软件的路径更加平滑. 这是由于A*算法和蚁群算法将地图分割为小的栅格，由当前栅格节点到下一个栅格节点的路径选择如图3(a)所示，因此，A*算法和蚁群算法路径由与坐标轴平行或夹角为45°的线段组成；Pathfinder采用三角形网格,如图3(b)所示，在三角形网格内，Pathfinder软件允许任意角度的疏散路线能够直接向目标点方向疏散，而蚁群及A*算法受限于栅格，只能沿与坐标轴平行或成45°的方向疏散，导致路径规划结果的长度比Pathfinder软件大. 笔者进行了多次小尺寸路径规划结果对比，A*算法和Pathfinder软件结果相似，验证了此A*算法在小尺寸模型路径规划方面的可靠性.

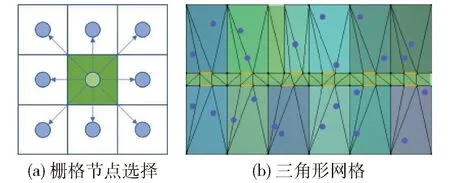
图3 网格示意图Fig.3 Sketch map of gridding

2.2 基于重庆某深埋地铁车站大尺寸模型

为了进一步比较不同算法的适用性，本文建立了重庆某埋深为53.24 m的地铁站站厅层实体模型，其平面尺寸为219.5 m×24.5 m，选取地图中部楼梯口处为起点(绿色节点)，左上角出口为目标出口，进行逃生疏散路线的规划. 不同算法路径规划结果如图4所示. 3种方法在深地空间大尺寸模型的路径距离、计算时间如表2所示.

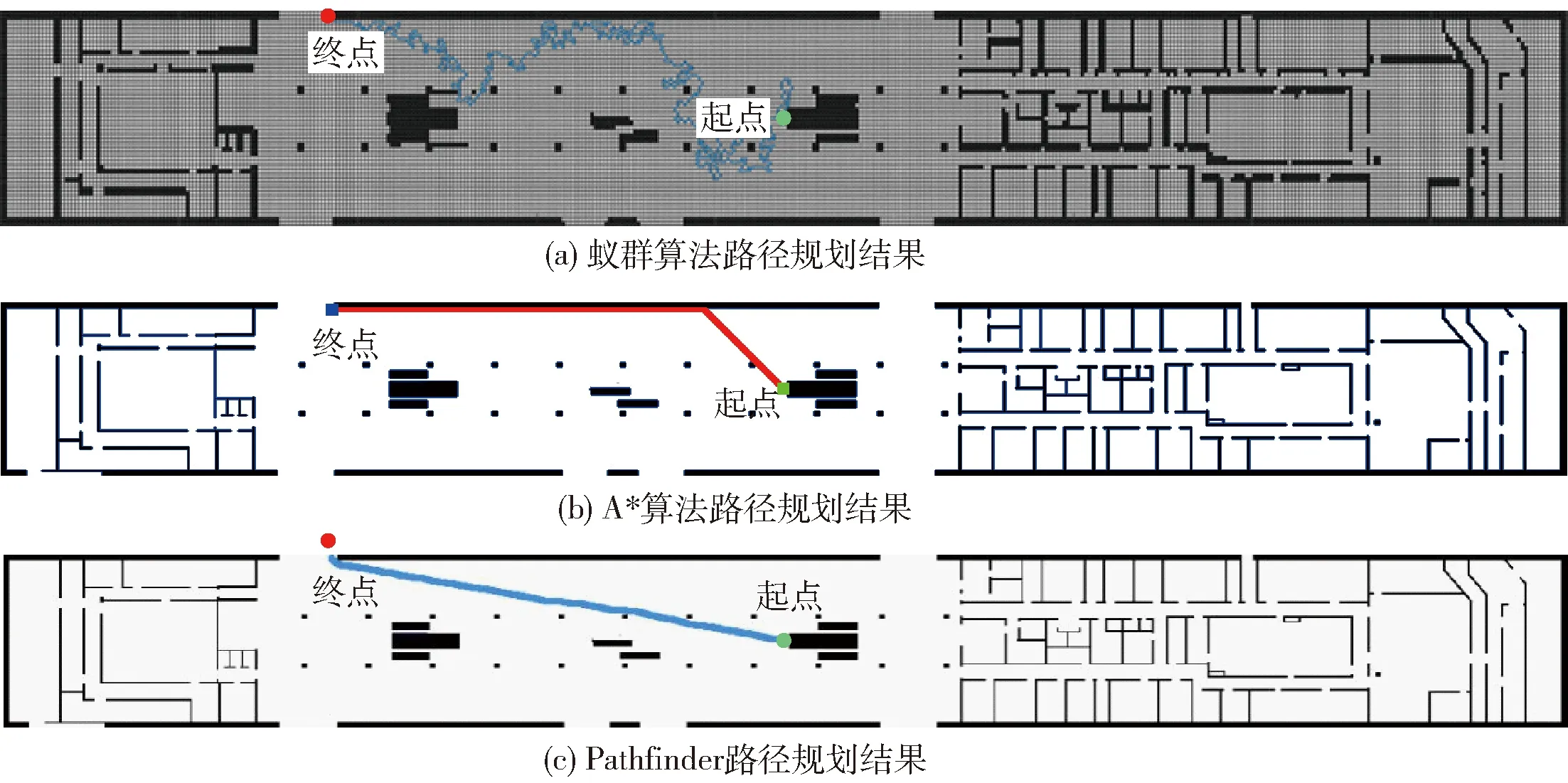
图4 路径规划结果对比Fig.4 Comparison of path planning results

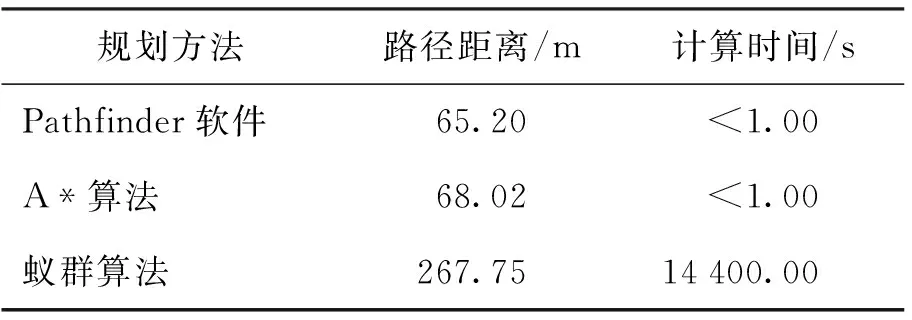
表2 大尺寸模型路径规划方法效果对比

由上述结果可知，在大尺寸模型的计算中，基本蚁群算法不能满足火灾条件下动态疏散路径规划计算时间短、路径规划距离短的要求，需要做进一步改进和优化. 而A*算法与Pathfinder软件结果相似，计算时间短，距离上的差异主要由图3所示的栅格节点选择方式导致. 除去上述结果，笔者进行了多次大尺寸路径规划结果对比，A*算法和Pathfinder软件的结果相似且计算时间短. 由于本文算法在计算过程中将危险烟气假定为障碍物，类似于地下空间内的墙、柱等结构，其特性都是阻挡人员逃生，因此，在加入烟气条件后本质上同加入墙、柱等障碍物是相同的，由此可见，考虑烟气条件下此A*算法在大尺寸模型路径规划方面也是可靠的，可以作为火灾疏散路径动态规划的支撑算法.

3 基于A*的火灾疏散路径动态规划

3.1 基于A*的火灾疏散路径动态规划方法

火灾的发生发展是一个动态演化的过程，其中温度、烟雾和有害气体体积分数都会随着时间变化，而人员对于温度和CO体积分数的耐受程度是有一定限度的，逃生路线规划中需要避开这些超过人体耐受性指标的区域. 因此，结合火灾条件下的温度、CO体积分数进行疏散路径的动态规划是十分必要的，这能够避免人员走入危险区域造成进一步不必要的损失.

为此本文提出了一种可根据火灾场景演化来进行疏散路径动态规划的方法，如图5所示. 首先建立拟分析区域的建筑布局几何模型，并进行网格划分；根据假想的火灾灾源位置及初始条件利用火灾模拟软件进行火灾模拟，记录每个网格区域温度及烟气体积分数的时程数据；以时间、空间坐标为基点，建立分析区域温度及烟气体积分数时程数据库；初始化障碍物判别矩阵，将所有元素均设置为1，搜索时程数据库，找出时程数据库中温度或烟气体积分数超过人体耐受性指标的网格，将其障碍物判别矩阵值设置为0；将上述判别矩阵导入A*算法中，采用A*算法将判别矩阵中值为0的区域和墙、柱等人群不能通过的区域一同考虑为障碍物.

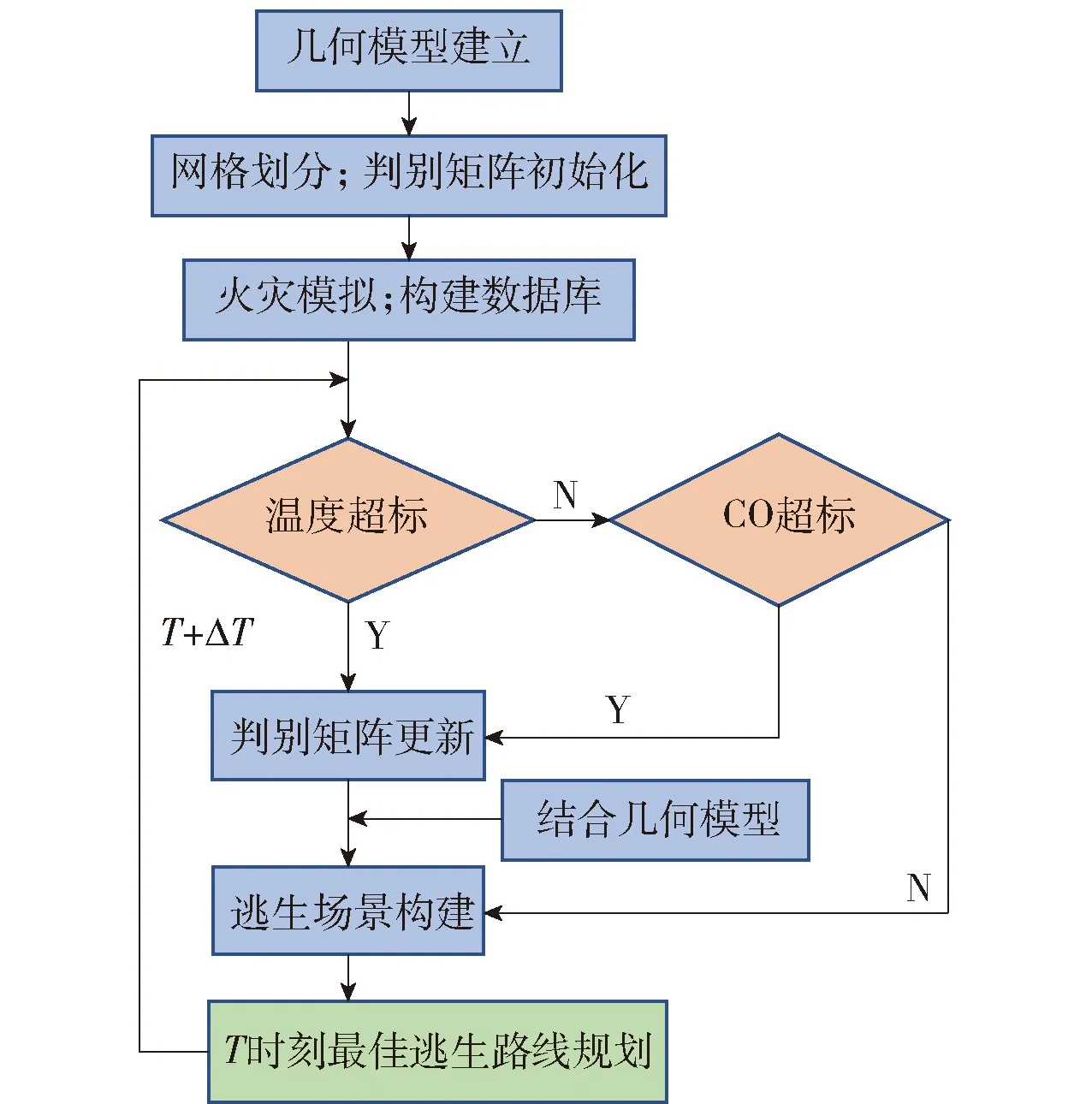
图5 疏散路径动态规划流程图Fig.5 Flow chart of dynamic evacuation path planning

3.2 重庆某深埋地铁车站火灾模拟

采用火灾模拟软件FDS模拟重庆某深埋地铁车站空间站厅层设备间区域配电室火灾时的工况，将地下空间结构墙、柱、楼梯表面设置为惰性，不参加燃烧，红色区域为火源，表面温度300 ℃，火焰温度1 427 ℃，辐射系数0.9，升温时间取默认值1 s，火灾功率按照中型火灾选取10 MW，站厅层中央顶板处布置通风口，风速3 m/s，在各出口区域设置通风条件为自由通风模式，传感器布设位置标注为黄色圆点，主要传感器GAS11用文字标注，如图6所示. 限于篇幅，仅列出200 s时温度及CO体积分数云图，如图7(a)(b)所示. 选取环控机房疏散路径上的传感器GAS11，提取出CO体积分数、温度时程曲线，见图8. 由图可知，在火灾发生发展过程中温度和CO体积分数都不断变化，当温度和CO体积分数指标超过人体耐受度即可将此区域划分为危险区域，并将其当作障碍物处理，有效避免人群走入危险区域.

图6 地铁车站模型俯视图(黄点为测点)Fig.6 Top view of the subway station model (yellow dots indicate measurement points)

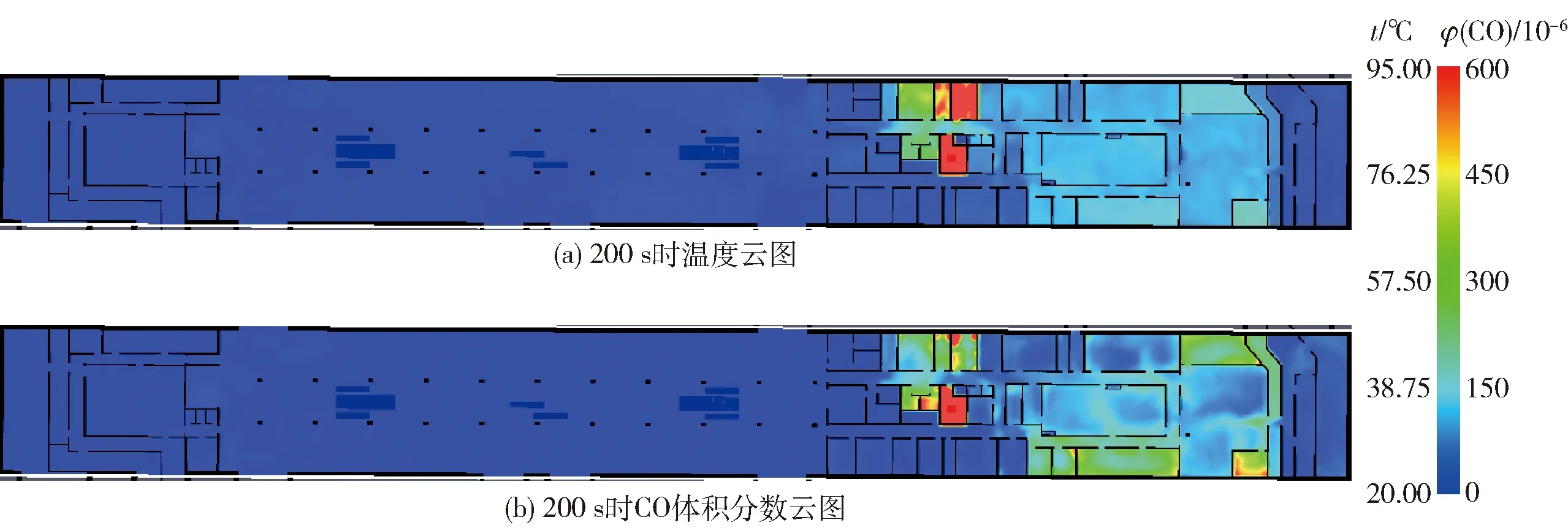
图7 火灾模拟结果示意图Fig.7 Sketch map of fire simulation results

图8 传感器GAS11的温度及CO体积分数时程曲线Fig.8 Time history curves of temperature and CO concentration measured at sensor GAS11

3.3 火灾动态疏散路径规划结果

结合火灾模拟结果，假定人员从环控机房开始逃生，利用A*算法进行动态疏散路径规划，寻找最优逃生路线并保证不走入危险区域. 限于篇幅，列出火灾发生后0、100、200、250、300 s时间节点的路径规划结果，如图9所示. 黑色区域表示温度和CO体积分数都超标的危险区域，灰色区域表示有一项超标的危险区域，都按照障碍物进行处理. 以环控机房为起点，在300 s内每隔5 s取样本点记录此时的疏散路径长度，绘制疏散路径长度时程图，如图10所示，其中疏散路径不存在的情况按照长度为正无穷进行记录.

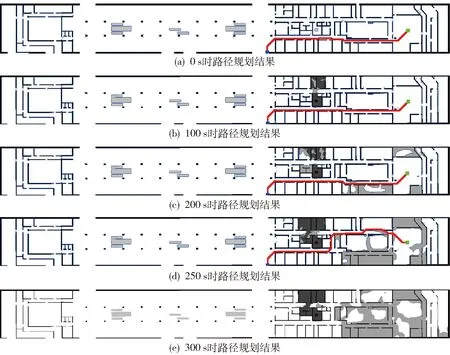
图9 不同时刻A*算法路径规划结果Fig.9 Path planning results of A* algorithm at different instants

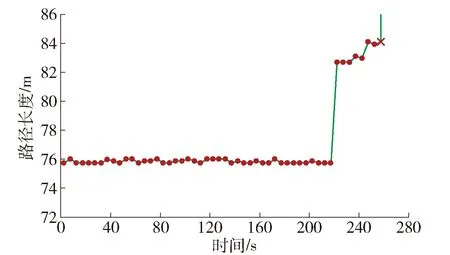
图10 疏散路径长度时程图Fig.10 Time history diagram of evacuation path length

人眼的特征高度在1.2～1.8 m，本文将1.6 m设为人眼的特征高度，分析火灾对人员疏散的影响. 相关研究显示，吸入气体超过60 ℃就能对人体造成不可恢复的损伤，因此，考虑将超过60 ℃的区域作为危险区域. NFPA130中规定，当火源周围CO体积分数达到250×10-6时将会威胁到疏散人员安全，因此，考虑将CO体积分数超过250×10-6的区域作为危险区域[12-14].

由路径规划结果可知，在0、100、200 s时以此环控机房内作为起点，最佳疏散路径是由下侧通道走向4号出入口. 在250 s时，此通道被高体积分数的CO阻挡，与0 s时进行对比，可以看出，算法自动规避危险区域并找到了另一条较长的路线. 在300 s时，不存在最佳疏散路线，超过该时间容易导致疏散过程中人员进入危险区域，造成进一步的伤亡[15].

由图8可知，在100、200 s时疏散路径上的传感器观测点GAS11处的CO体积分数在230 s左右时已经达到250×10-6，因此，该位置的人群应在火灾发生后230 s前尽快撤离.

由图10可以看出，疏散路径长度的变化具有“突变”的特征，这是因为在215～220 s，作为主要疏散路径的传感器GAS11所在通道被危险烟气完全阻挡，导致疏散路径变长，故可推断该火灾场景下最大允许疏散时间为215 s. 考虑到这种“突变”特征以及地下空间疏散通道的单一性，可以在主要疏散通道上设置智能的疏散路径指示设备，实时计算并提示此时此区域最佳逃生出口及路径，避免出现疏散过程混乱的情况[16].

4 结论

1) 基于小尺寸模型和某深埋地铁车站足尺模型系统对比了蚁群算法、A*算法及Pathfinder软件的路径规划长度及所需计算时间，发现A*算法可以达到与Pathfinder软件近似的路线规划结果且计算需时较短，而基本蚁群算法路径容易陷入局部最优且计算时间较长，因此，采用A*算法作为逃生疏散路线动态规划的支撑算法.

2) 提出了地下空间逃生疏散路线动态规划方法，该方法通过建立火灾场景关键指标的时程数据库，并基于人体耐受性指标确定不适合逃生的区域，进行逃生疏散路线的动态规划.

3) 基于重庆某深埋地铁站结合动态火灾模拟结果，将离地面1.6 m截面处超过60 ℃或CO体积分数超过250×10-6的区域连同车站内部墙、柱一并考虑为障碍物，利用提出的方法获得了不同时刻的最佳逃生疏散路线及该火灾场景下最大允许疏散时间，可指导消防救援方案的制定.

4) 未来可利用温度及CO传感器建立动态数据库，在火灾发生时根据反馈出高温及高体积分数CO的传感器位置确定危险区域，构建不同时刻的逃生场景，并利用A*算法得到不同时刻的最佳逃生路线，使逃生疏散路线更加高效和准确.