带翼缘开洞剪力墙抗震性能
2021-07-14王越宇刘其舟
钱 凯, 王越宇, 李 治, 刘其舟
(1.广西大学土木建筑工程学院, 南宁 530004; 2.桂林理工大学土木与建筑工程学院, 广西 桂林 541004)
剪力墙是高层建筑中应用最为广泛的关键抗侧力构件,对结构的抗震性能至关重要. 为探究剪力墙的抗震性能,研究人员开展了大量的研究工作. Lefas等[1]通过试验研究普通钢筋混凝土剪力墙的强度、变形特征和破坏机理. 曹万林等[2-3]、张建伟等[4-6]、杨兴民等[7]通过系列试验研究,探讨单排配筋混凝土剪力墙的抗震性能,并给出相应的承载力计算公式. Maier[8]通过试验研究3片矩形剪力墙和7片工字形剪力墙的抗震性能,结果表明:带翼缘试件的抗剪承载力远高于矩形试件. 章红梅等[9]通过试验研究4片不同轴压比的矩形剪力墙的抗震性能,结果表明:随着轴压比的增加,试件屈服强度和延性等均表现出先增大后减小的规律. 李红运等[10]采用有限元程序VecTor2对带边缘构件剪力墙抗震抗剪承载力进行分析,结果表明:当剪跨比为1.0和1.5时,随着边缘构件截面面积和纵筋配筋率的增大,剪力墙抗震抗剪承载力相应增加. 李青宁等[11]对12片不同边缘构件短肢剪力墙和2片T形普通剪力墙进行试验研究,结果表明:短肢剪力墙的破坏形式主要为弯剪破坏,在水平荷载作用下,非对称截面短肢剪力墙的强度和刚度呈现出非对称特点. 叶燕华等[12]通过试验研究5片预制双板内浇自密实混凝土剪力墙的抗震性能,结果表明:预制双板内浇自密实混凝土剪力墙具有良好的抗震性能,且增大轴压比和设置暗柱均有利于改善墙体的抗震性能.
在结构设计时,因为窗户、门洞等原因,需要在墙壁上开洞,当洞口较大或者较靠近边界区域时,可能会对钢筋混凝土剪力墙的抗震性能产生不可忽略的影响. 然而,与实心剪力墙相比,目前开洞钢筋混凝土剪力墙的研究相对较少. 曹万林等[13]设计2个带洞口的剪力墙,通过试验研究承载力、延性等性能,并给出单排配筋带洞口剪力墙的承载力计算模型. 王激扬等[14]通过试验研究开洞面积和开洞位置对矩形剪力墙抗震性能的影响,验证应用开洞折减率计算剪力墙水平极限承载力的可行性. Ali等[15]通过一系列试验研究交错门洞对钢筋混凝土剪力墙的影响,研究结果表明:靠近边界区域的门洞可能会消除面内约束并导致剪切破坏. 贺晶方等[16]通过试验研究开洞大小对短肢剪力墙抗震性能的影响,结果表明:随着洞口尺寸增大,试件极限承载力有所下降,但延性提高,耗能能力也有所增强. Yanez等[17]通过试验研究不规则开洞的钢筋混凝土矩形墙的抗震性能,研究结果表明:在开洞率较小的情形下,开洞尺寸和布置对墙体在低周往复荷载作用下的性能没有显著的影响. 汪梦甫等[18]比较非线性有限元分析和试验的结果,验证静力非线性pushover有限元分析方法,评估开洞剪力墙抗震性能的可靠性. 马银等[19]采用MATLAB编程计算不规则开洞对矩形剪力墙抗震性能的影响,并与有限元分析结果进行对比,结果发现不规则开洞会使墙体底端应力集中现象加剧. 陈怀亮等[20]对已有抗剪抵抗机构进行改进,提出新的矩形开洞剪力墙极限承载力分析模型,比较2种模型的承载力计算值和试验值,结果表明:改进后的模型计算结果和试验结果吻合更好,具有较高的精确度. 上述研究主要针对开洞剪力墙,但对于带翼缘开洞剪力墙方面的研究则较少. 为此,Qian等[21]对带翼缘的开洞钢筋混凝土剪力墙进行低周反复加载试验研究,但由于试件数量有限,一些关键参数对带翼缘开洞剪力墙抗震性能的影响规律仍有待进一步探讨.
基于以上原因,本文对Qian等[21]的开洞剪力墙试验进行数值模拟,通过与试验结果对比验证有限元模型的可靠性,并通过大量有限元参数分析探究翼缘、开洞率、轴压比、剪跨比等对带翼缘开洞剪力墙抗震性能的影响,研究可为带翼缘开洞剪力墙的设计及应用提供参考依据.
1 试验简介
为研究翼缘对开洞剪力墙抗震性能的影响,Qian等[21]对带翼缘开洞钢筋混凝土剪力墙进行低周反复加载试验,见图1. 剪力墙试件的厚度为120 mm. 其中,S-F1、S-F3试件的混凝土平均抗压强度实测值为35.0MPa. 钢筋实测材料性能见表1.

图1 试件尺寸及配筋图(单位:mm)Fig.1 Dimensions and reinforcement details of specimens (unit: mm)

表1 钢筋材性
试验加载装置如图2所示. 需要说明的是, S-F系列试件是参考Yanez等[17]的S系列试件的试验设计的,而Yanez等[17]的试验未对剪力墙施加轴压力,因此S-F系列试件的轴压比为0. 试验加载制度如图3所示. 试验采用荷载- 位移联合控制方式加载. 第1阶段按荷载控制并分级加载,其中P是试件的理论极限承载力. 第2阶段按位移控制,以图3

图2 加载装置Fig.2 Test setup

图3 加载制度示意图Fig.3 Loading protocol
所示的屈服位移Δy值的倍数为级差控制加载.
2 有限元模型
2.1 单元选取
为进一步探讨翼缘、开洞率、轴压比、剪跨比等对带翼缘开洞剪力墙抗震性能的影响,采用通用有限元软件ABAQUS对S-F1、S-F3试件进行精细化模拟分析,其中混凝土采用三维实体单元C3D8R,钢筋采用三维桁架单元T3D2,采用Embedded连接关系将钢筋嵌入混凝土单元中,不考虑钢筋与混凝土之间的黏结滑移.
2.2 材料本构
混凝土材料采用损伤塑性模型,该模型能够有效反映混凝土材料抗拉强度和抗压强度之间的差异,以及加载过程中刚度及强度的退化.
随着损伤发展,混凝土的弹性刚度D会不断退化,D可表示为
D=(1-d)D0
(1)
式中:D0为材料的初始弹性刚度;d为材料的损伤因子.
混凝土的受拉损伤因子dt和受压损伤因子dc可分别表达[22]为
(2)
(3)
式中:εc为抗压塑性应变;εt为抗拉塑性应变;Ec为混凝土初始弹性模量;bc为抗拉塑性应变和抗压非弹性应变的比值;bt为抗压塑性应变和抗拉非弹性应变的比值;σt为混凝土损伤状态时的拉应力;σc为混凝土损伤状态时的压应力.
钢筋采用双折线弹塑性本构模型,它的应力- 应变关系包括弹性段和强化段,见图4,Es为钢筋弹性模量,fy为屈服强度,εy为屈服应变.
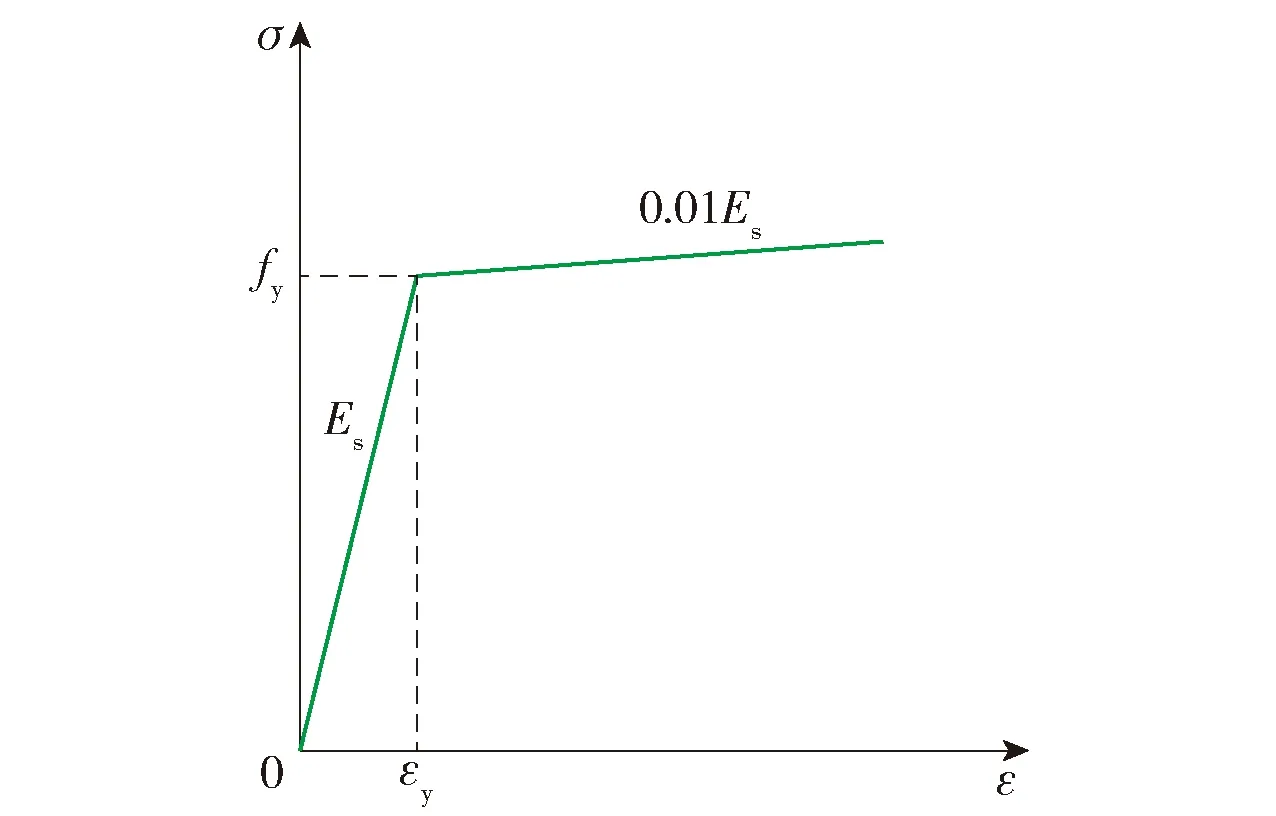
图4 钢筋应力- 应变双折线模型Fig.4 Stress-strain double line model of reinforcement
2.3 边界条件
模型的基础梁采用固定约束,加载梁一端与参考点耦合,在参考点上施加位移进行单向推覆分析. 有限元模型如图5所示. 需要说明的是,虽然S-F系列试件的轴压比为0,但是之后的有限元参数分析中仍然需要考虑轴压比的影响,因此,图5显示了参数分析中轴向力的施加位置.

图5 开洞混凝土剪力墙有限元模型Fig.5 Finite element model of concrete shear wall with opening
3 有限元验证
3.1 荷载- 位移骨架曲线
单向推覆分析荷载- 位移骨架曲线计算值与试验值对比见图6. 总体而言,骨架曲线计算值与试验值基本吻合,两者的峰值荷载相差均在10%以内,说明建立的有限元模型能够有效预测试件的荷载- 位移关系.

图6 模拟和试验荷载- 位移骨架曲线对比Fig.6 Comparison of backbone envelopes of load-displacement curves between simulation and test
3.2 破坏形态
有限元及试验的最终破坏形态对比见图7. 采用最大和最小主塑性应变云图来反映混凝土的破坏. 可以看到,理论结果与试验结果吻合较好.
4 拓展参数分析
4.1 开洞率
为进一步研究开洞大小对带翼缘和洞口的剪力墙抗震性能的影响,保持洞口与边缘的距离,改变洞口大小. 需要说明的是,由于原试验在洞口较小时,洞口与地梁存在一定的距离,而在洞口较大时,洞口与地梁的距离为0,因此,本文建立与S-F系列试验相对应的不同开洞率的剪力墙有限元模型,不考虑洞口相对地梁位置对承载力的影响,模型见表2,其中模型编号为S-F-m,m为开洞率,可表示为
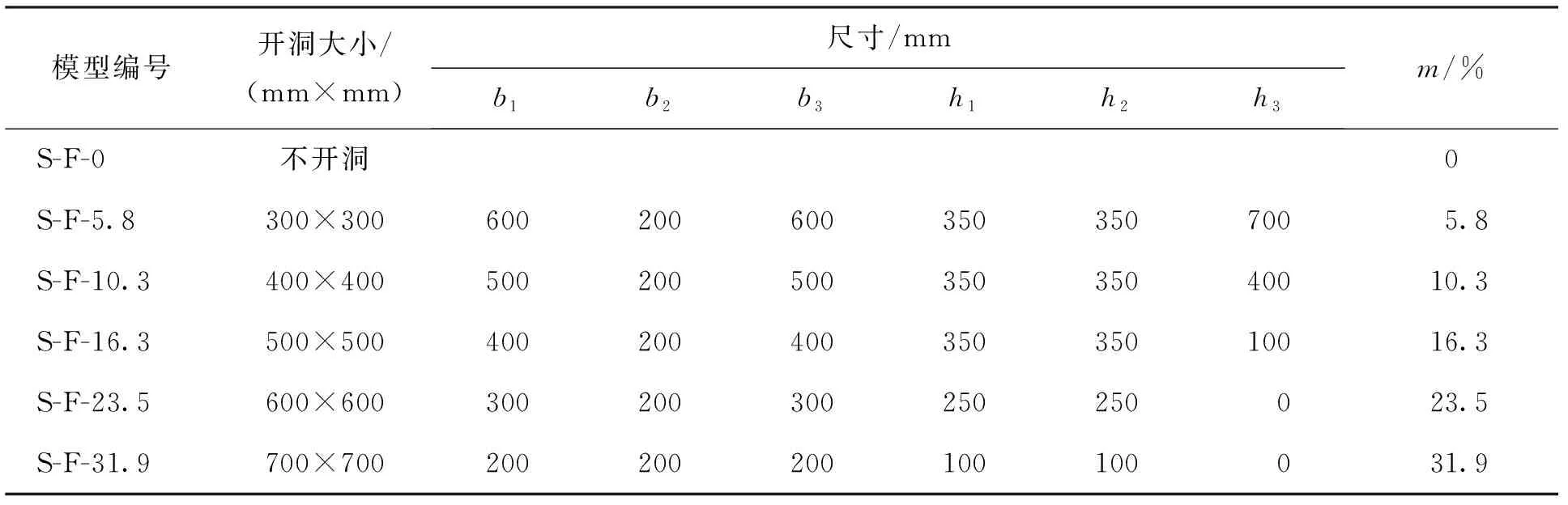
表2 模型开洞率
(4)
式中:A0为洞口面积;Aw为墙体正立面投影面积.有限元模型洞口的所处部位通过参数b1、b2、b3、h1、h2、h3进行确定,见图8.图9为不同开洞率的有限元模型的荷载- 位移骨架曲线.

图8 模型开洞位置Fig.8 Models opening location
由图9可知,S-F-5.8和S-F-10.3剪力墙极限承载力相较于不开洞剪力墙反而有所上升,这是由于模型根据美国混凝土结构规范ACI318-05[23]的构造要求,在洞口附近附加一定的纵向受力钢筋,当开洞率较小时,附加钢筋的强化效果超过洞口造成的承载力损失导致的. 开洞率较小且满足规范基

图9 S-F-m系列模型单向推覆荷载- 位移曲线Fig.9 Load-displacement skeleton curves of S-F-m series models
本要求时,计算剪力墙极限承载力时可不考虑洞口的削弱. 此外,随着开洞率上升,剪力墙延性先升后降. 当开洞率不大于16%时,带洞口剪力墙的极限位移均大于无洞口剪力墙,且随着开洞率增加极限位移逐步提高. 当开洞率大于16%时,剪力墙的极限位移逐步减小.
假定S-F-m模型的极限承载力为Fm,令α=Fm/F0,其中,F0表示m=0时模型的极限承载力,则α随m的变化如图10所示.

图10 α与m相互关系Fig.10 Relationship between α and m
将图10的散点进行曲线拟合,可得到表征α与m之间相互关系的数学表达式
α=27m3-17m2+1.8m+1
(5)
令α≥1,则m≤0.13,即,若剪力墙满足规范构造要求,则当m<13%时,可以不考虑剪力墙极限承载力的削弱.结合图9可知,当m<13%时,可以不考虑剪力墙极限位移的削弱.
为了研究附加纵向钢筋的影响,在S-F-m系列模型的基础上去除附加纵向钢筋,建立同等开洞率的有限元系列模型S-F-mt,S-F-mt系列有限元模型的单向推覆荷载- 位移曲线见图11.
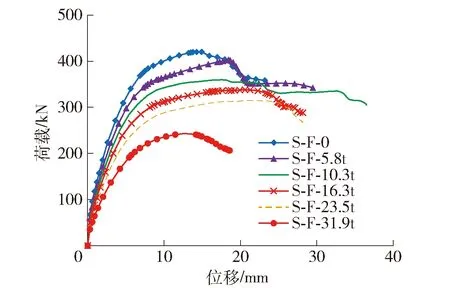
图11 S-F-mt系列模型荷载- 位移骨架曲线Fig.11 Load-displacement skeleton curves of S-F-mt series models
假定S-F-mt的极限承载力为Fmt,令αt=Fmt/F0t,其中,F0t表示m=0时模型的极限承载力,则αt随m的变化如图12所示.
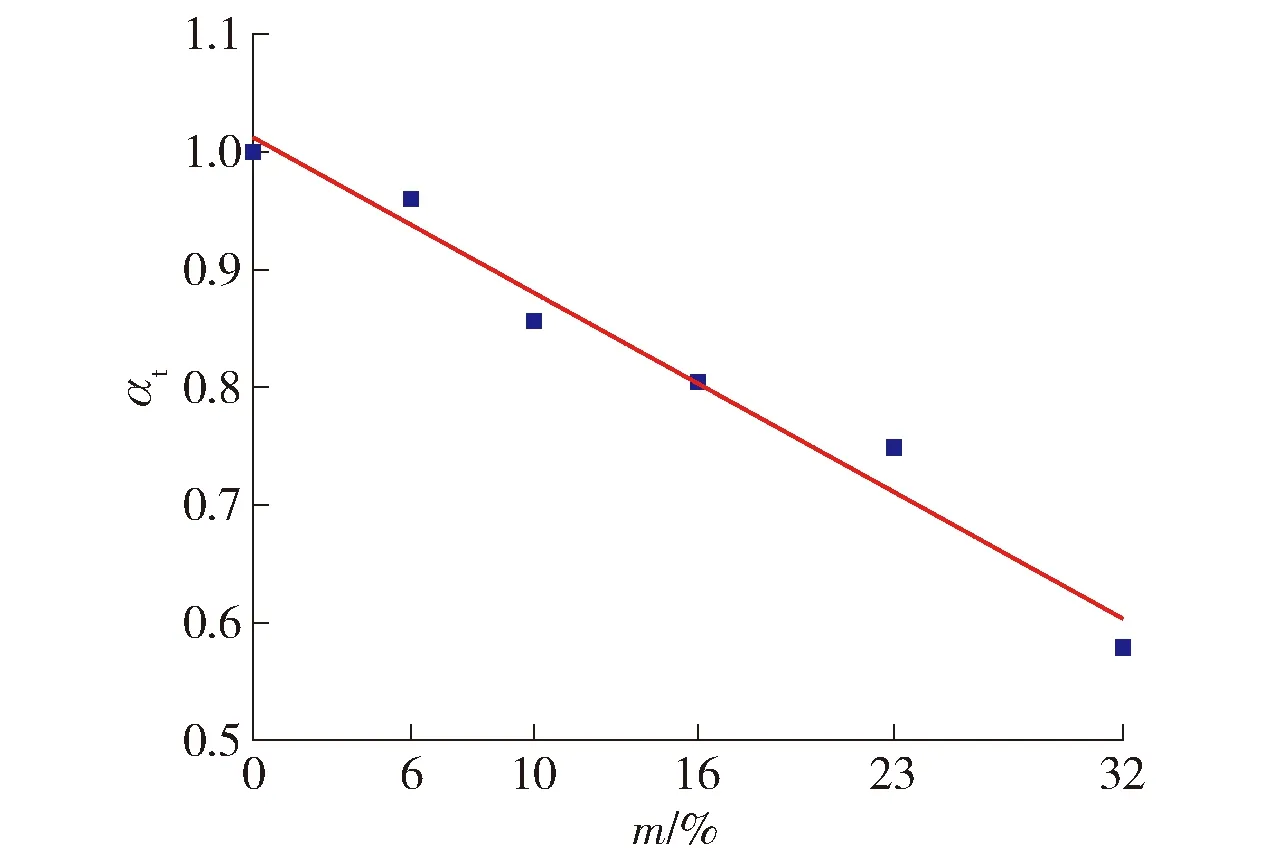
图12 αt与m相互关系Fig.12 Relationship between αt and m
将图12的散点进行曲线拟合,可得到表征αt与m之间相互关系的数学表达式
αt=-1.28m+1
(6)
由公式(6)可知,若移除附加钢筋,在m<30%时,随着开洞率提高,剪力墙极限承载力几乎呈现线性下降的趋势.
4.2 翼缘形状
为研究翼缘形状对开洞剪力墙抗震性能的影响规律,建立带不同形状翼缘的剪力墙有限元模型,见图13. 其中,S1、S3为Yanez等[17]试验中的试件,x代表数字1或3,S-Fx系列为Qian等[21]试验中的试件,S-Fx-T、S-Fx-DZ、S-Fx-L系列则是相应S-Fx试件将翼缘形状分别改变为T形、带端柱、L形的有限元模型.

图13 翼缘形状及配筋(单位:mm)Fig.13 Flange shape and reinforcement (unit: mm)
图14为有限元模型的单向加载荷载- 位移曲线. 其中(+)和(-)分别代表图13的右和左方向加载. 由图14可知,对于带翼缘剪力墙而言,开洞剪力墙的延性高于无洞口剪力墙. 仅布置单侧翼缘时,开洞剪力墙在负向加载时的延性高于正向加载时的延性,但低于同等条件下双侧翼缘开洞剪力墙的延性.

图14 模型荷载- 位移骨架曲线Fig.14 Load-displacement skeleton curves of models
带翼缘剪力墙的极限承载力均高于无翼缘剪力墙,但延性均有不同程度的下降. 仅布置单侧翼缘时,剪力墙正向加载极限承载力与双翼缘剪力墙相当,而负向极限承载力有非常明显的下降,但负向加载时的延性要高于正向推覆的延性. 可以看到,无论是否带有洞口,虽然T形翼缘剪力墙正向极限承载力明显大于L形,但其负向极限承载力与L型相差不大.
4.3 轴压比及剪跨比耦合影响规律分析
4.3.1 有限元模型
为探究轴压比(n)及剪跨比(λ)对带翼缘和洞口剪力墙抗震性能的影响规律,建立编号分别为S-F1-0.5、S-F1-0.75、S-F1-1.15、S-F1-1.50、S-F1-2.00、S-F3-0.38、S-F3-0.76、S-F3-1.15、S-F3-1.53、S-F3-1.92的有限元模型. 以S-F3-0.76为例,见图15,其编号0.76代表其剪跨比为0.76,其他参数,如尺寸、配筋、开洞率等则与模型S-F3完全一致.

图15 S-F3-0.76有限元模型Fig.15 Finite element model of S-F3-0.76
4.3.2 轴压比影响规律
图16为不同轴压比有限元模型在单向推覆分析时的荷载- 位移骨架曲线.

图16 不同轴压比模型荷载- 位移骨架曲线Fig.16 Load-displacement skeleton curves of different axial compression ratio models
以n作为横坐标,假定模型S-Fx-λ在n下的极限承载力为Fn,令αn=Fn/F0,则可得到αn与n之间的相互关系,见图17.

图17 αn与n相互关系Fig.17 Relationship between αn and n
将图17的散点进行曲线拟合,可得到图17中的数学表达式.
对于未开洞剪力墙而言,由图16、17可知,当λ=0.75时,剪力墙极限承载力随n增加成线性增长,拟合曲线的斜率约为1.6.延性随n的增加逐步下降.当剪力墙λ=1.15时,他们的极限承载力随n先增加后降低,n=0.5是升降的拐点,剪力墙延性随n增加逐渐降低.当剪力墙λ=1.50时,极限承载力随n的增加先增加后降低,n=0.30是升降的拐点,剪力墙延性随轴压比增加先有所提高后逐渐降低.
当剪力墙m=23%且λ<1.15时,它们的极限承载力随n的增长先提高后降低,增长曲线的斜率小于未开洞剪力墙,下降曲线的斜率则大于未开洞剪力墙.极限承载力增长与降低的拐点轴压比则小于未开洞剪力墙.当剪力墙λ>1.15时,开洞剪力墙极限承载力的变化规律逐渐与未开洞剪力墙逐渐保持一致.无论轴压比及剪跨比如何变化,开洞剪力墙的延性均大于未开洞剪力墙.
4.3.3 剪跨比影响规律
图18为相同轴压比不同剪跨比有限元模型的荷载- 位移骨架曲线.
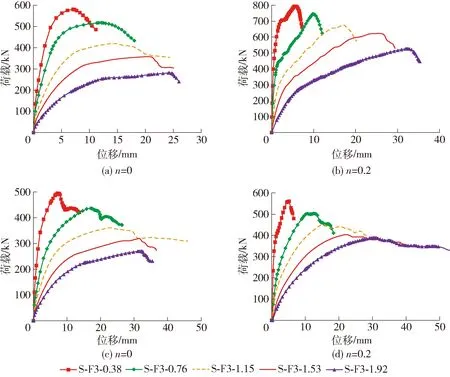
图18 荷载- 位移骨架曲线Fig.18 Load-displacement skeleton curves of models
以λ作为横坐标,假定模型S-Fx-λ在λ下的极限承载力为Fλ,令αλ=Fλ/F1.15,F1.15代表λ=1.15时的极限承载力,则可得到αλ与λ之间的相互关系见图19.
将图19的散点进行曲线拟合,可得到图19中的数学表达式.
由图19可知,n一定时,αλ均随着λ的提高基本呈线性规律递减,而延性则随λ提高逐渐提高.是否开洞并不会明显改变αλ与λ之间的线性关系,区别在于开洞会造成拟合曲线斜率的变化.n=0时,随λ的提高,开洞剪力墙极限承载力拟合曲线下降的斜率比不开洞剪力墙减少约18%.当n=0.20时,随λ的提高,开洞剪力墙拟合曲线斜率与不开洞剪力墙相当.
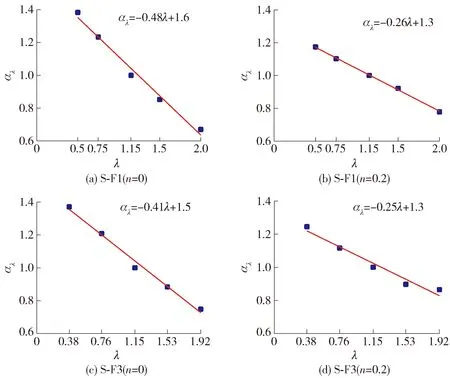
图19 αλ与λ相互关系Fig.19 Relationship between αλ and λ
4.4 剪跨比及轴压比横向对比分析
以λ和n为变量的剪力墙极限承载力变化曲面如图20所示,其中A、B、C、D分别为曲面的4个角点,S3为Yanez等[17]试验中的试件.

图20 极限承载力变化曲面Fig.20 Curved surface of ultimate load
对比S-F1及S-F3的承载力曲面可知:
1) 从AB边至DC边方向,曲面S-F3相对于S-F1的下坠趋势愈发明显,说明随n增大,洞口对剪力墙极限承载力的劣化影响也逐渐增大.
2) 从BC至AD方向,曲面S-F3与S-F1均逐步上升,区别在于S-F3相对于S-F1的上升趋势较为平缓,说明洞口对剪力墙极限承载力的劣化影响会随着λ的减小有所增大.
对比S-F3与S3的承载力曲面可知,两者的承载力曲面形状相差不大,区别在于S-F1相较于S3而言承载力更大,说明翼缘主要作用是提高了开洞剪力墙的极限承载力. 在D点附近,曲面S-F3相对于曲面S3有一个明显上扬角. 说明在低剪跨比且高轴压比的情况下,翼缘对剪力墙极限承载力的强化作用更为明显.
5 结论
采用ABAQUS建立了剪力墙的非线性有限元模型,与试验结构对比验证了模型的正确性,之后通过参数分析可以得出:
1) 若满足规范基本要求,则当剪力墙开洞率小于13%时,可以不考虑剪力墙极限承载力和延性的削弱.
2) 若无附加钢筋的影响,随着开洞率提高,带翼缘开洞剪力墙极限承载力呈线性下降的趋势.
3) 开洞剪力墙的延性高于无洞口剪力墙. 仅布置单侧翼缘时,为便于描述,规定翼缘受拉为正,受压为负,则开洞剪力墙的负向加载延性高于正向加载延性,但低于同等条件下双侧翼缘开洞剪力墙的延性.
4) 带翼缘剪力墙的极限承载力高于无翼缘剪力墙,但延性有一定程度的下降. 仅布置单侧翼缘时,剪力墙正向推覆极限承载力与双翼缘剪力墙相当,而负向极限承载力有非常明显的下降,但负向加载时的延性要高于正向加载时的延性.
5) 随轴压比的增大或剪跨比的减小,洞口对剪力墙极限承载力的劣化影响也逐渐增大.
6) 在低剪跨比且高轴压比的条件下,翼缘对开洞剪力墙极限承载力的强化作用更为明显.
