4 m高度同轴馈电线栅型垂直极化EMP辐射波模拟器的辐射特性分析

朱湘琴，吴 伟，贾 伟

(西北核技术研究所，西安710024；强脉冲辐射环境模拟与效应国家重点实验室，西安710024)

强电磁脉冲可通过孔缝或天线耦合到电子设备的连接线缆上感应出强瞬态电磁干扰，影响电子设备的正常工作，甚至导致电子设备损伤失效[1-4]。垂直极化电磁脉冲(EMP)模拟器由于能提供主极化电场分量为垂直分量的源区高空EMP环境，所以得到了广泛的研究[1-2]。垂直极化EMP模拟器主要分为EMP有界波模拟器[5-15]和EMP辐射波模拟器[16-20]。针对垂直极化EMP辐射波模拟器的辐射场特性，文献[17]和文献[18]分别基于传输线模型及并行时域有限差分(FDTD)方法，研究了加载电阻的线栅型模拟器的辐射场特性，文献[18]还针对高度为15 m的模拟器，研究了离散电阻加载对辐射场的影响；文献[19]将轴对称FDTD方法与基尔霍夫表面积分表达式相结合，给出了全部金属实体模型模拟器辐射近场的快速估算方法；文献[20]对与峰化电容器一体化设计的模拟器辐射场进行了模拟分析，给出了含有峰化电容器的模拟器辐射场与理想锥形模拟器天线辐射场时域波形的区别，讨论了峰化电容器内芯长度及电极端面半锥角对模拟器辐射场的影响。但到目前为止，国内外文献中尚未见报道线栅型垂直极化EMP辐射波模拟器架设前各类设计参数对辐射场的影响及加载电阻对模拟器有效测试区的影响。

本文以高度为4 m的同轴馈电线栅型垂直极化EMP辐射波模拟器为研究对象，将完全理想磁导体(PMC)镜像法[21]用于同轴馈电模拟器辐射场特性的并行FDTD计算中，研究了模拟器的线栅截数、底部金属实体圆锥的高度、线栅的数目、线栅半径及模拟器架设时的介质支撑圆柱等因素对模拟器辐射场的影响，并给出了加载电阻对模拟器有效测试区的影响。

1计算模型

线栅型垂直极化EMP辐射波模拟器的简化计算模型，如图1所示。该模型的外形与单锥天线相似，主要由底部的金属实体圆锥、从金属实体圆锥的圆形截面边缘向锥顶所拉的金属线栅及铺设在地面上的金属垫网所构成。模拟器的高度为H，顶部半径为r，对应的半锥角为α；实体圆锥的高度为Hc。若在模拟器的顶部最高处拉上网格足够小的金属网，则模拟时可将金属网盖当作实体金属盖进行处理。本文中，假设地面铺设的金属网为无限大。

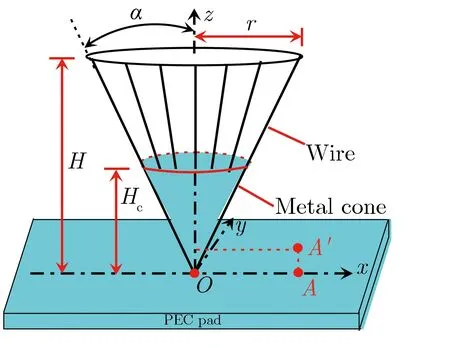
图1线栅型垂直极化EMP辐射波模拟器的简化计算模型Fig.1Simple model of wire vertically polarizedEMP radiating-wave simulator

采用同轴馈电的方式对模拟器进行馈电，馈电电压为标准的双指数脉冲，其表达式为[22]

U(t)=V0(e-ζt-e-βt)

(1)

其中， 当V0=0.391×106V，ζ=4.0×107s-1，β=6.0×108s-1时，对应的脉冲电压峰值约为300 kV，上升沿及半高宽分别为2.46 ns和23 ns。

2模拟方法及验证

根据模拟器辐射场的对称性，分别以xOz平面和yOz平面为PMC对称面，将两个PMC对称面包围的区域称为PMC对称面的内侧区域(x≥0且y≥0)，并对该区域采用基于PMC镜像法[21]的并行FDTD方法计算辐射场。根据PMC镜像原理，对PMC边界上的切向电场强度进行迭代时，使用该PMC边界内侧的切向磁场强度分量负值替代外侧对称位置的切向磁场强度，将PMC对称面外侧区域的法向电场强度赋值为0。

同轴馈电线附近的FDTD网格，如图2所示。

(a)On yOz plane

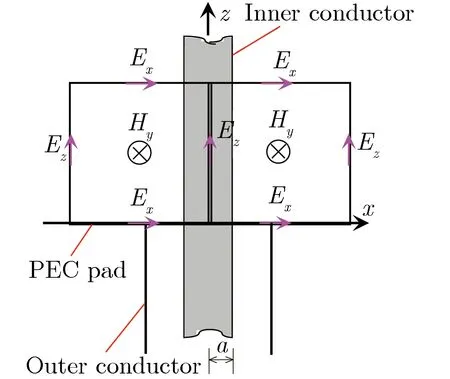
(b)On xOz plane

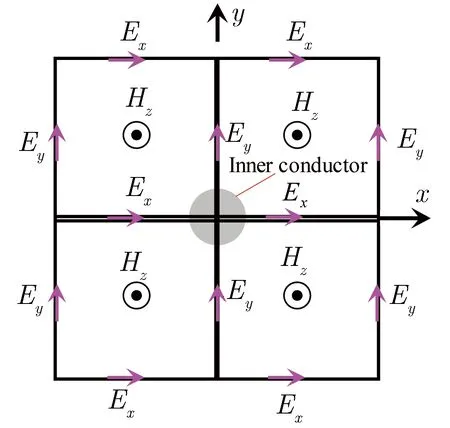
(c)On xOy plane 图2同轴馈电线附近的FDTD网格Fig.2FDTD grids near coaxial transmission line

(2)

将j≤-1的PMC对称面外侧的磁场强度x分量赋值为0，j>0的PMC对称面内侧的磁场强度x分量按照无对称时的常规FDTD公式进行迭代。

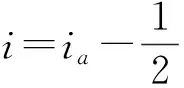
(3)

将i≤-1的PMC对称面外侧的磁场强度y分量赋值为零，i>0的PMC对称面内侧的磁场强度y分量按照无对称时的常规FDTD公式进行迭代。

若以xOz平面及yOz平面为PMC对称面，则由图2(c)可知，两个PMC对称面外侧的磁场强度z分量可赋值为0，对称面内侧的磁场强度z分量可按照常规FDTD公式进行迭代。

设图1中模拟器高度H为4 m，顶部半径r为2.5 m，半锥角α为32°。为保证同轴线的阻抗与模拟器天线的阻抗匹配，设置同轴线的特性阻抗为75 Ω[25-26]。取底部金属实体圆锥的高度Hc为1.1 m，线栅数目Nt为48，线栅半径rd为2.5 mm。FDTD模拟时， 3个方向的网格尺寸均设为5 mm。用本文模拟方法及商用软件模拟得到辐射场中测点A(4 m, 0 m, 0 m)和A′(4 m, 0 m, 0.2 m) 的电场强度Ez时域波形对比，如图3所示。由图3可见，本文模拟方法与商用软件的模拟结果符合较好，证明了本文模拟方法的可靠性和准确性。

(a)A(4 m, 0 m, 0 m)

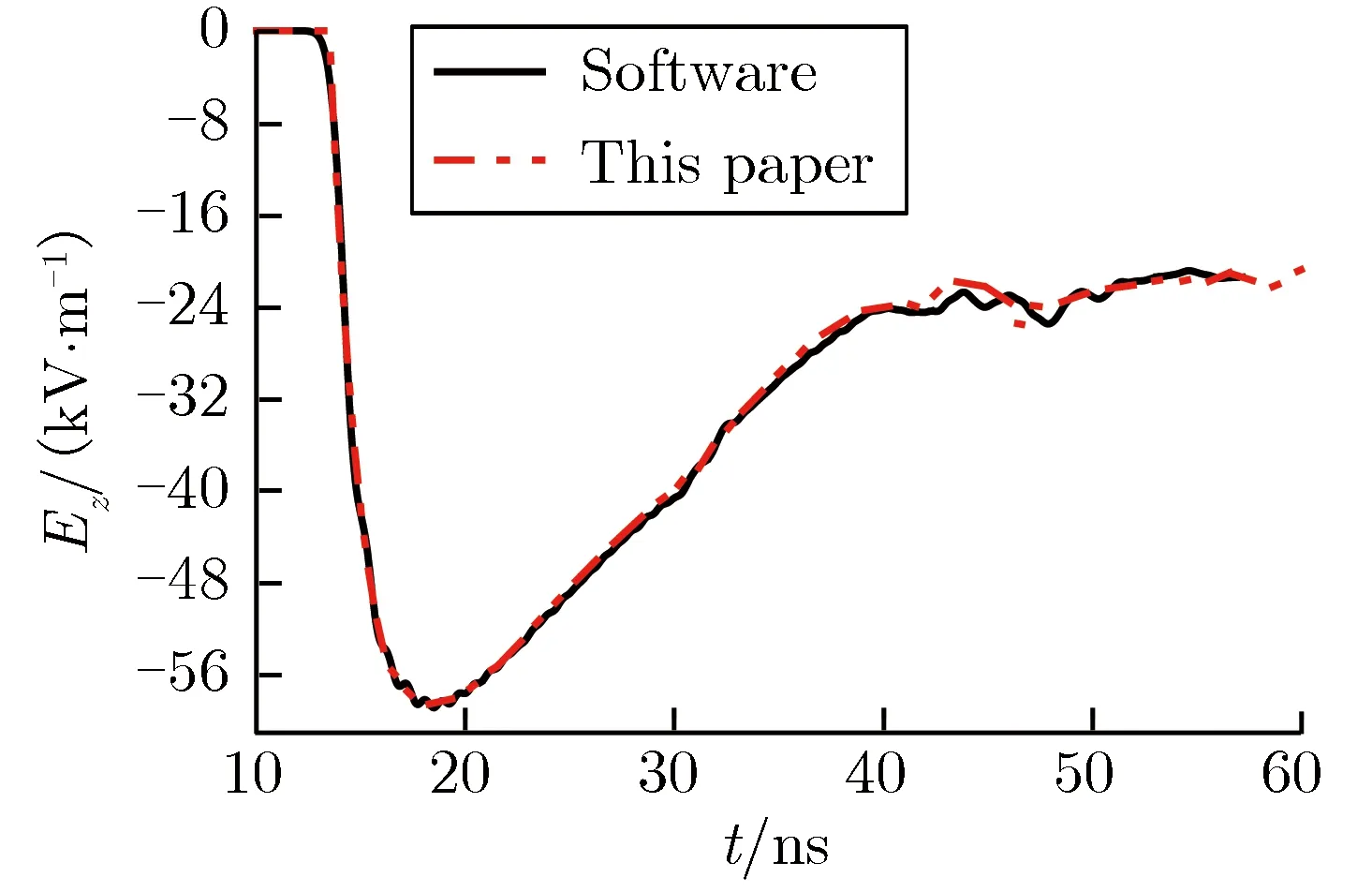
(b)A′(4 m, 0 m, 0.2 m) 图3两种模拟方法得到的电场强度时域波形对比Fig.3Comparison of electric field strength in time-domainwaveforms obtained by two simulation methods

3模拟结果与分析

本文计算中，设模拟器高度H为4 m，顶部半径r为2.5m，半锥角α为32°，且保持不变。在模拟器的顶部设有金属网盖。为保证模拟结果的准确性，计算时FDTD的网格尺寸与线栅的直径相同。虽然模拟器高度只有4 m，但由于线栅半径为毫米量级，故所取的FDTD网格尺寸很小，计算中总网格数可达109量级。

3.1线栅截数对辐射场的影响

设实体圆锥的高度Hc为1.1 m，线栅半径rd为2.5 mm。将图1中的线栅模型由一截改为两截，图4为两截线栅模型的示意图。设下截线栅高度为H1；下截线栅数目Nt1为40，上截线栅数目Nt2为20。

模拟得到H1变化时，测点A(4 m, 0 m, 0 m)和A′(4 m, 0 m, 0.2 m)的电场强度时域波形，如图5所示。为方便比较，图5中还给出了一截线栅模型且线栅数目Nt为40时的模拟结果及全部实体金属模型的模拟结果。由图5可见，与一截线栅模型的计算结果相比，两截线栅模型得到的辐射场时域波形存在明显的突变，与全部实体金属模型的模拟结果偏离更远，这主要是由于两截线栅连接处的电流不连续造成的。与全部实体金属模型的辐射场时域波形相比，H1越高，波形出现变化的时间越滞后，且波形开始变化的时刻对应着两截线栅连接处到测点的最短光程。因此，模拟器设计时，建议采用一截线栅模型。本文后续研究中均采用一截线栅模型。

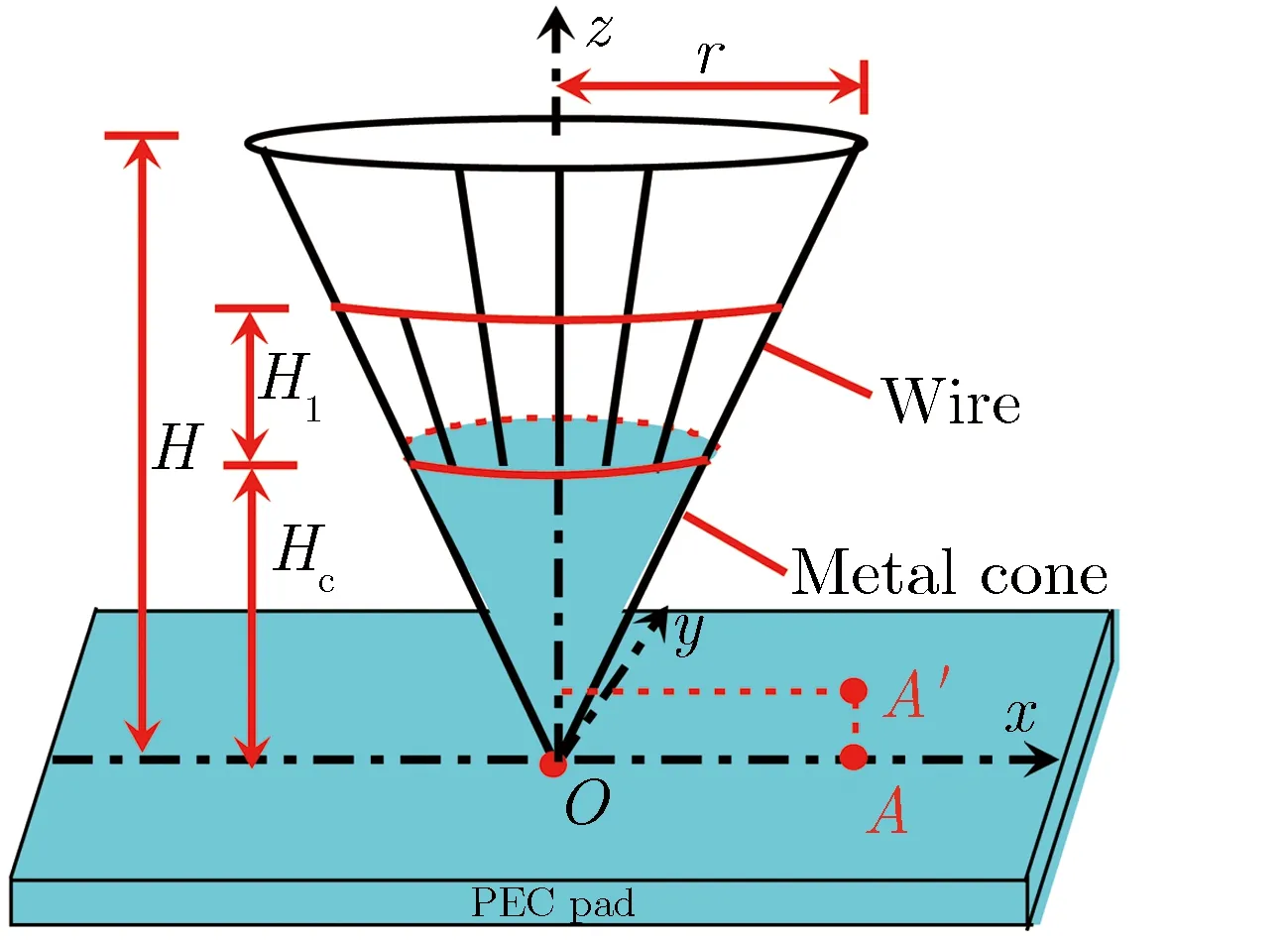
图4两截线栅模型的示意图Fig.4Model of a simulator with two wire-section

(a)A(4 m, 0 m, 0 m)

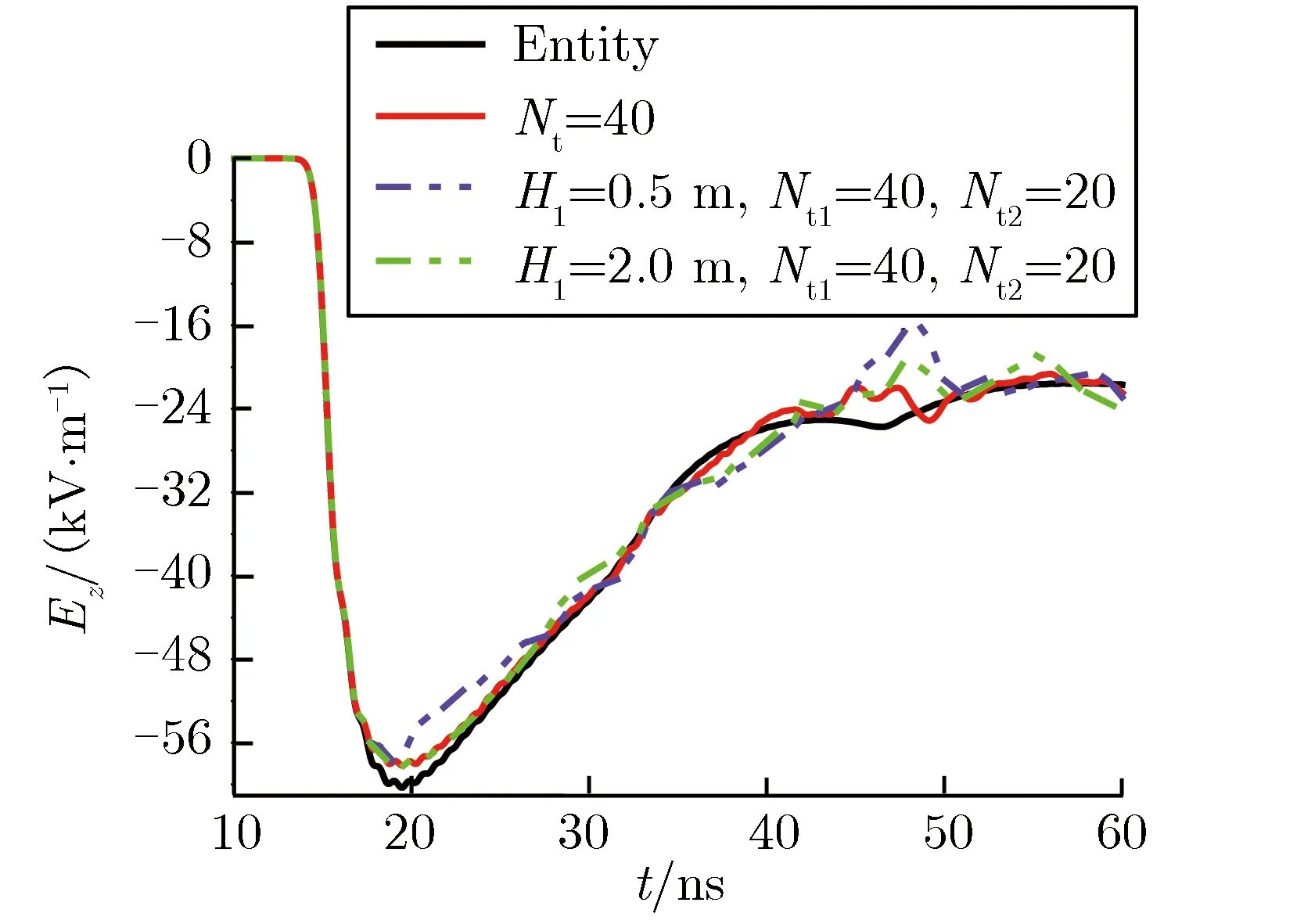
(b)A′(4 m, 0 m, 0.2 m) 图5线栅截数及H1变化时计算得到的电场强度时域波形对比Fig.5Comparison of electric field strength in time-domain waveforms with different wire-section’s number and H1

3.2实体圆锥高度对辐射场的影响

设模拟器线栅数目Nt为30。模拟得到实体圆锥高度Hc分别为0.5， 1.1， 2.5 m时，测点A(4 m, 0 m, 0 m)和A′(4 m, 0 m, 0.2 m)的电场强度峰值Ez,max、上升沿tr和半高宽tw，如表1所列。电场强度时域波形，如图6所示。为方便比较，表1和图6还给出了全部实体金属模型的模拟结果。

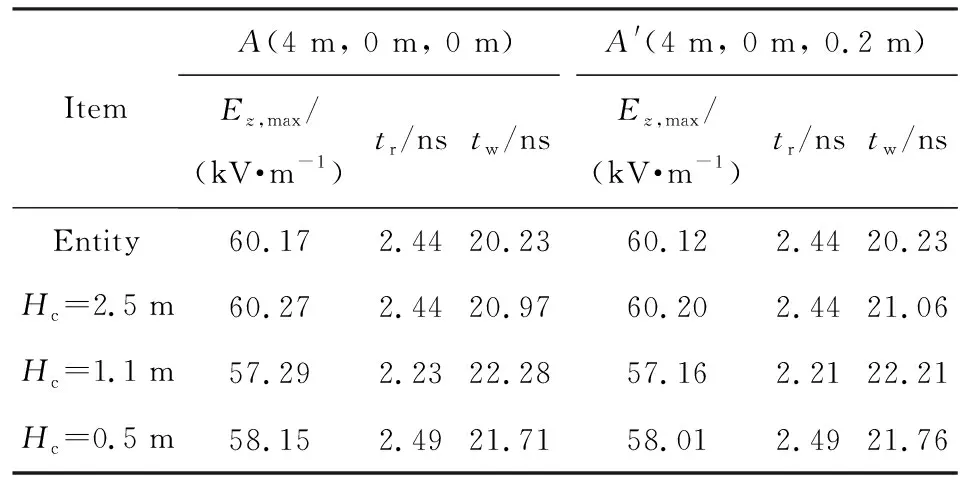
表1实体圆锥高度变化时的电场强度峰值、上升沿及半高宽Tab.1Comparison of the peak-value, rise-time, and FWHMof electric field strength with different Hc

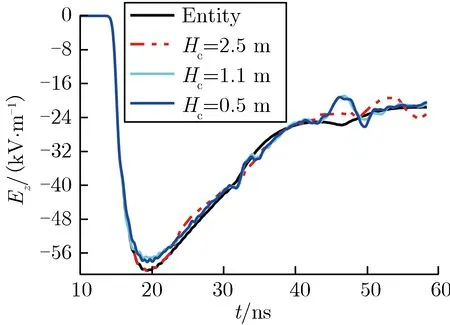
(a)A(4 m, 0 m, 0 m)

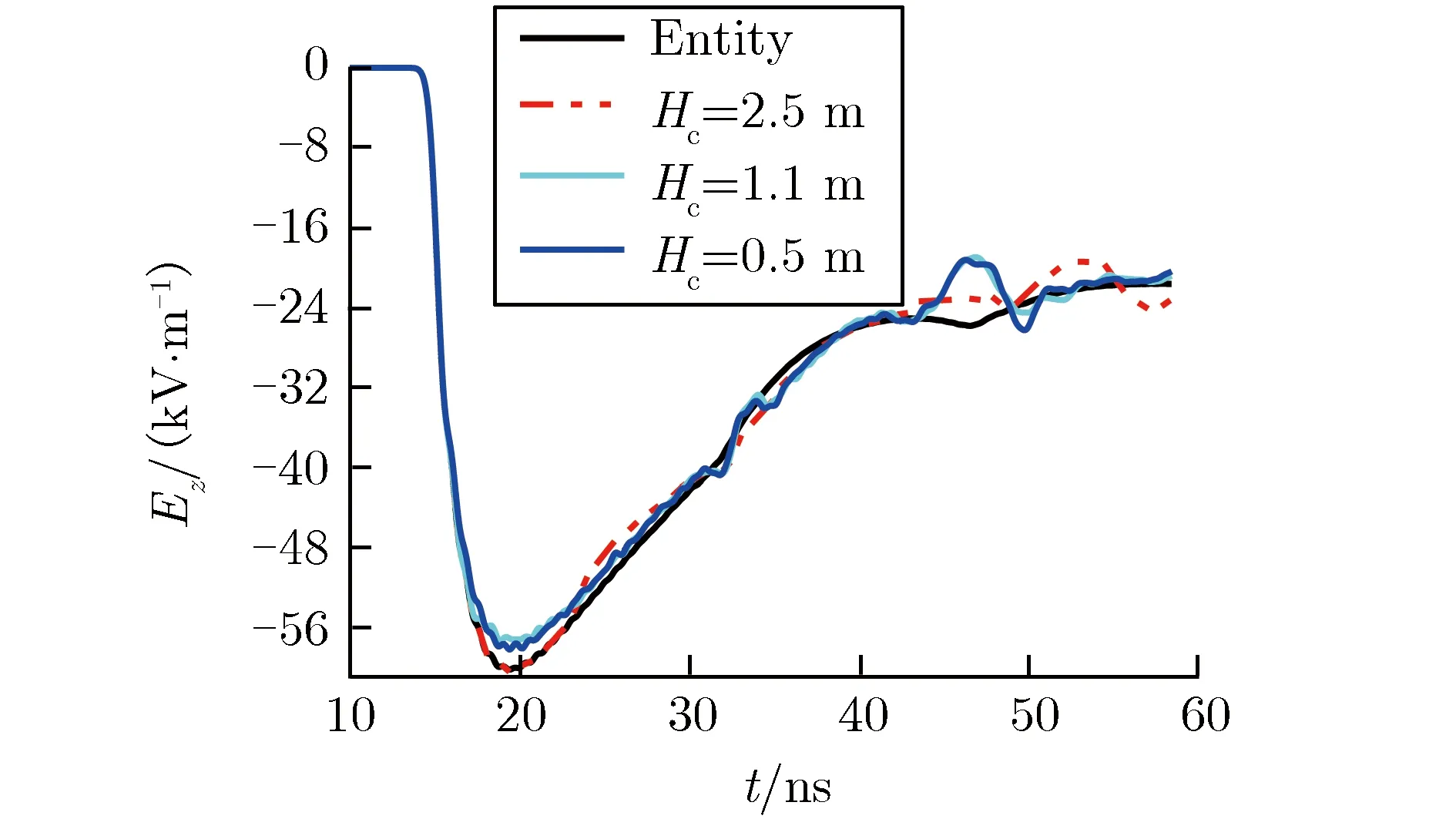
(b)A′(4 m, 0 m, 0.2 m) 图6实体圆锥高度变化时的电场强度时域波形对比Fig.6Comparison of electric field strength intime-domain with different Hc

由表1及图6可见，与全部实体金属模型的计算结果相比，线栅模型中测点辐射场时域波形发生变化的时刻与锥-线连接处的位置有关，即与实体圆锥的高度Hc有关。实体圆锥的高度越高，锥-线连接处对辐射场时域波形的作用越滞后，时域波形越接近全部实体金属模型的计算结果。当Hc分别取0.5, 1.1, 2.5 m时，预估得到锥-线连接处与激励源对测点A(4 m, 0 m, 0 m)作用的最短光程差对应分别为1.03, 2.67, 8.13 ns；当Hc从0.5 m增加到2.5 m时，锥-线连接处对测点作用的时刻晚于电场强度峰值的出现时刻，导致Hc为2.5 m时测点的电场强度峰值及上升沿与全部实体金属模型的计算结果几乎一致。当Hc在0.5～2.5 m变化时，两个测点的电场强度峰值与全部实体金属模型电场强度峰值的相对偏差均小于5%。为确保线栅模型中测点的电场强度峰值与全部实体金属模型相同，模拟器设计时实体圆锥必须达到一定的高度。

3.3线栅数目对辐射场的影响

设实体圆锥的高度Hc为1.1 m。模拟得到线栅数目Nt变化时，测点A(4 m, 0 m, 0 m)和A′(4 m, 0 m, 0.2 m)的电场强度峰值Ez，max、上升沿tr和半高宽tw，如表2所列。Nt分别为24， 30， 60时的电场强度时域波形，如图7所示。

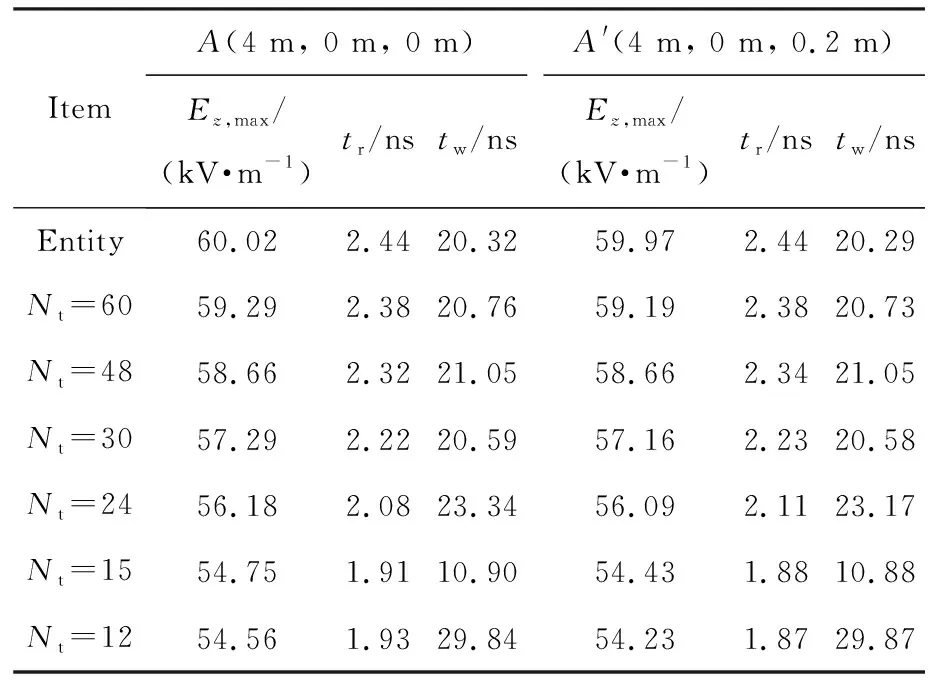
表2线栅数目变化时的电场强度峰值、上升沿及半高宽Tab.2Comparison of the peak-value, rise-time, and FWHMof electric field strength with different Nt

(a)A(4 m, 0 m, 0 m)

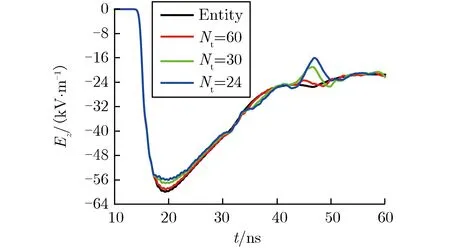
(b)A′(4 m, 0 m, 0.2 m) 图7线栅数目变化时的电场强度时域波形对比Fig.7Comparison of electric field strength intime-domain with different Nt

结合表2和图7可见，不同线栅数目下，测点的电场强度峰值与全部实体金属模型相比都发生了变化。这是由于从激励源到锥-线连接处的最短光程与锥-线连接处到测点的最短光程之和，大于从激励源直接到达测点的最短光程，二者之差，对于A点和A′点分别为2.62 ns和2.41 ns，即锥-线连接处对各测点电场强度时域波形开始作用的时刻均位于时域波形到达峰值的时刻之前，所以锥-线连接处会对各测点的电场强度峰值产生影响。与全部实体金属模型的计算结果相比，线栅数目越少，测点电场强度时域波形的变化越大，电场强度峰值减小的幅度越大。这是因为线栅数目的减小，会导致模拟器表面电流传输能力减弱，从而使模拟器辐射的能量减小。当线栅数目在24～60变化时，两个测点的上升沿均满足(2.5±0.5) ns、半高宽均满足(23±5) ns的IEC-61000-4-25技术指标要求[27]。因此，当线栅数目在24～60变化时，电场强度峰值、上升沿及半高宽这3个要素中，可以只用电场强度峰值作为选择线栅数目的依据。此时，若以不小于全部实体金属模型电场强度峰值的95%或93%作为线栅数目的选择依据，则选取线栅数目为30根或24根即可满足要求。

3.4线栅半径对辐射场的影响

设实体圆锥的高度Hc为1.1 m，线栅数目Nt为24。模拟得到线栅半径rd分别为1.5, 2.5, 4 mm时,A(4 m, 0 m, 0 m)和A′(4 m, 0 m, 0.2 m) 电场强度峰值、上升沿和半高宽，如表3所列。时域波形如图8所示。由表3和图8可见，当线栅半径越大时，测点辐射场的模拟结果与全部实体金属模型越接近。但线栅半径在1.5～4 mm变化时，同一测点的电场强度时域波形几乎没有差别，上升沿几乎一致，电场强度峰值和半高宽的最大相对偏差分别不超过1.3%和3.6%，这是由于线栅半径的变化较小，远小于激励源的最小波长的缘故。与全部实体金属模型相比，线栅半径在1.5～4 mm变化时，测点的电场强度峰值均能达到全部实体金属模型的93%。因此，实验设计时线栅半径可取为1.5～4 mm。

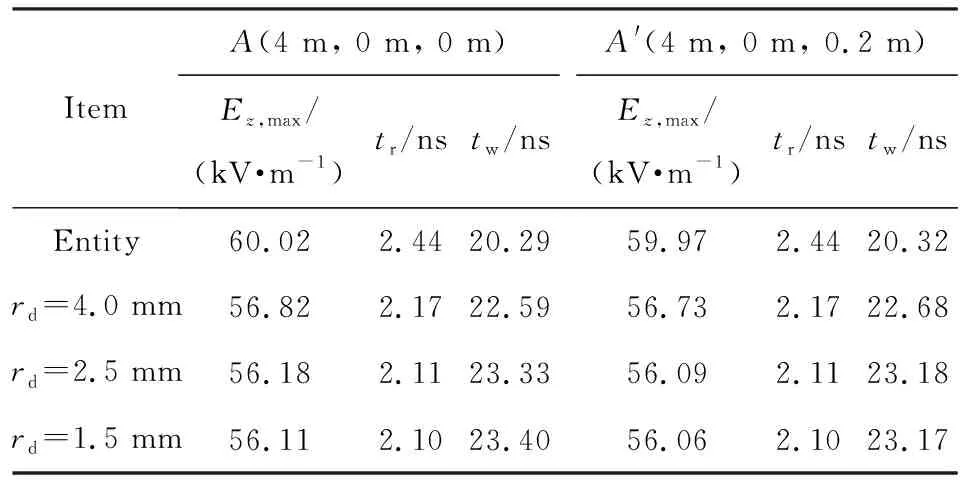
表3线栅半径变化时的电场强度峰值、上升沿及半高宽Tab.3Comparison of the peak-value, rise-time, andFWHM of electric field strength with different rd

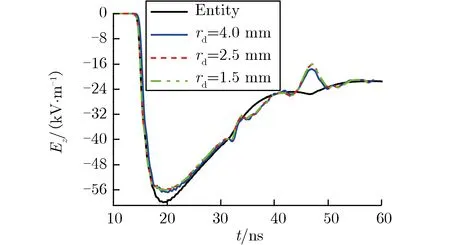
(a)A(4 m, 0 m, 0 m)

(b)A′(4 m, 0 m, 0.2 m) 图8线栅半径变化时的电场强度时域波形对比Fig.8Comparison of electric field strengthin time-domain with different rd

3.5介质支撑圆柱对辐射场的影响

设实体圆锥的高度Hc为1.1 m，线栅半径rd为2.5 mm，线栅数目Nt为30。在模拟器周围设置4根与模拟器等高的空心介质支撑圆柱，圆柱外径rw为0.216 m，壁厚为72 mm，相邻支撑圆柱的中心间距dz为3 m。图9为含有介质支撑圆柱模拟器的模型俯视图。模拟计算时，假设介质支撑圆柱壁为非导电的均匀介质，相对介电常数为5.5。除选择位于2个支撑圆柱对称面上且与中轴线的间距为4 m的测点A(4 m, 0 m, 0 m)及A′(4 m, 0 m, 0.2 m)为监测点外，还选择与中轴线的间距为4 m且位于2个支撑圆柱对角线延长线上的测点B(2.828 m, 2.828 m, 0 m)及其上方高度为0.2 m的B′(2.828 m, 2.828 m, 0.2 m)为监测点。模拟得到有、无介质支撑圆柱时，测点的电场强度峰值、上升沿和半高宽，如表4所列。电场强度时域波形，如图10所示。为便于比较，表4中和图10中均给出了无支撑圆柱的全部实体金属模型的模拟结果。

结合表4和图10可见：1)无论有、无支撑圆柱存在，线栅模型中同一位置测点的电场强度峰值都小于全部实体金属模型的情形。2)与无支撑圆柱的线栅模型相比，有支撑圆柱的线栅模型中，同一位置测点的电场强度峰值均增加；位于支撑圆柱对角线延长线上的测点B和测点B′的上升沿变快，而位于2个支撑圆柱对称面上的测点A和测点A′的上升沿变慢；且当有支撑圆柱时，测点A和测点A′的电场强度时域波形在峰值附近出现了严重的畸变，畸变开始出现的时刻与关于x轴对称的2个支撑圆柱对测点作用的最短光程一致，说明波形畸变是由这2个支撑圆柱对测点辐射场干扰叠加引起的。因此，建议实验时的验收点不能选择在相邻圆柱的对称面上，而应选择在支撑圆柱对角线的延长线上。此外，为使实验时测点电场强度时域波形的上升沿满足 (2.5±0.5) ns的技术指标，应将脉冲源的上升沿减慢。

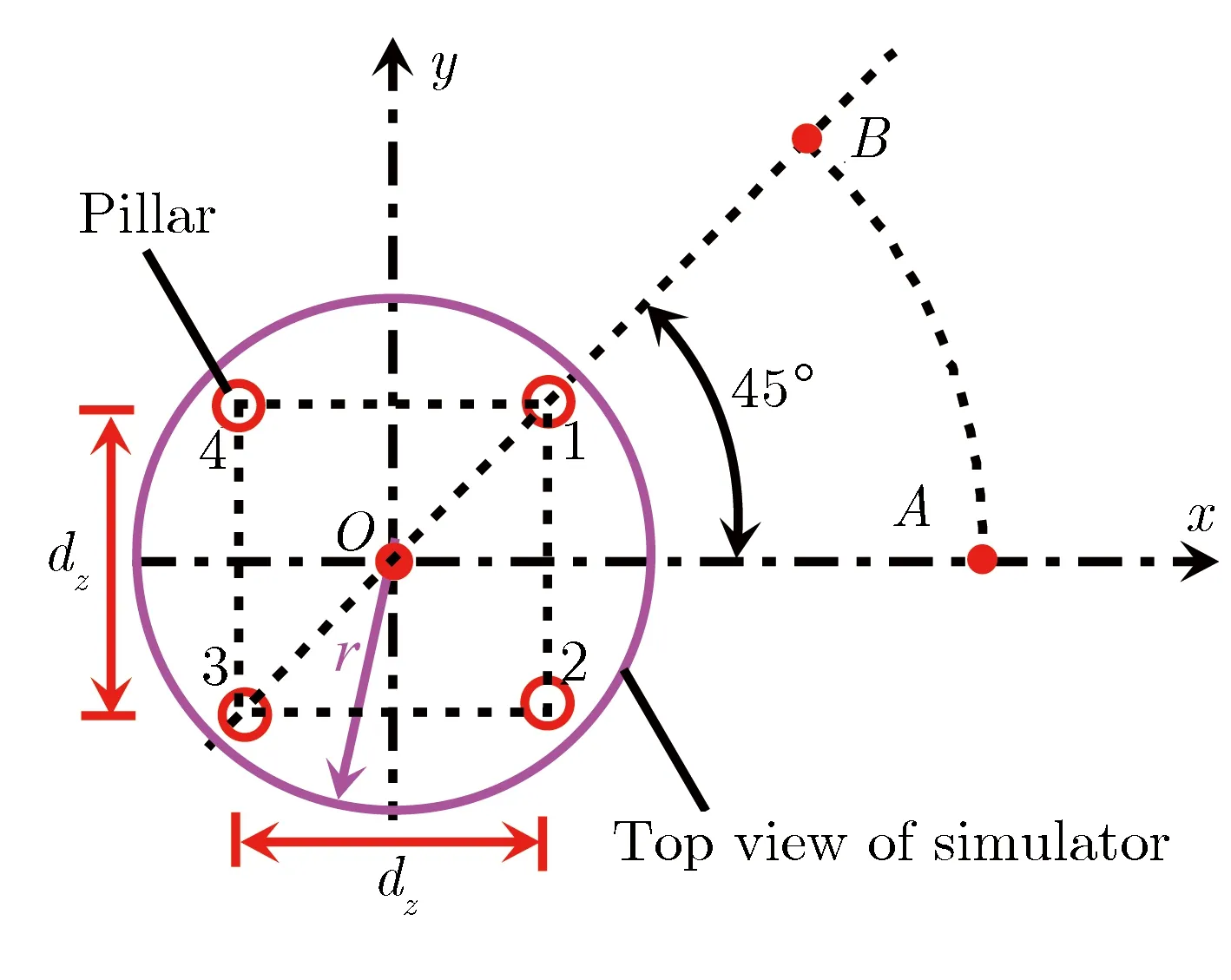
图9含有介质支撑圆柱模拟器的模型俯视图Fig.9Top view of the simulator with pillars

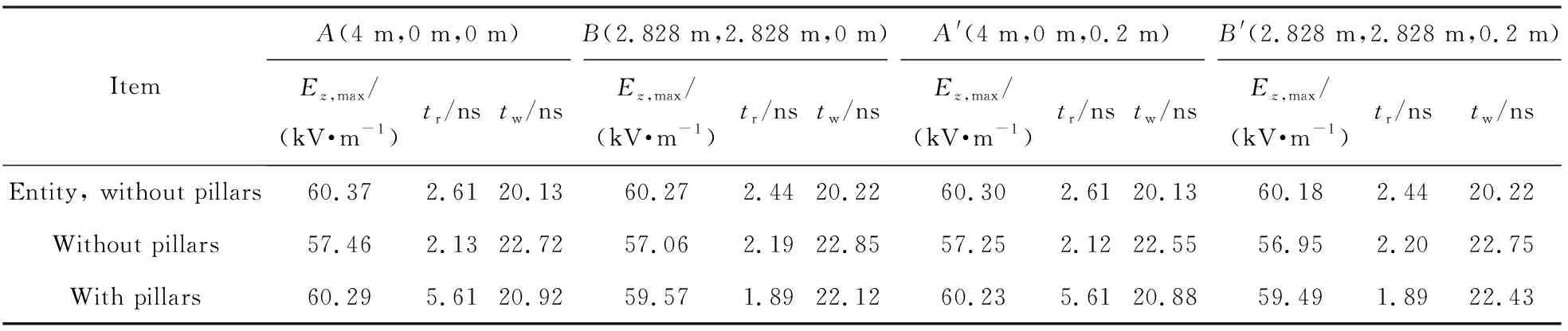
表4有、无介质支撑圆柱下的电场强度峰值、上升沿和半高宽Tab.4Comparison of the peak-value, rise-time, and FWHM of electric field strength with or without pillars

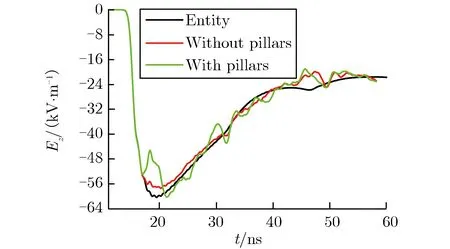
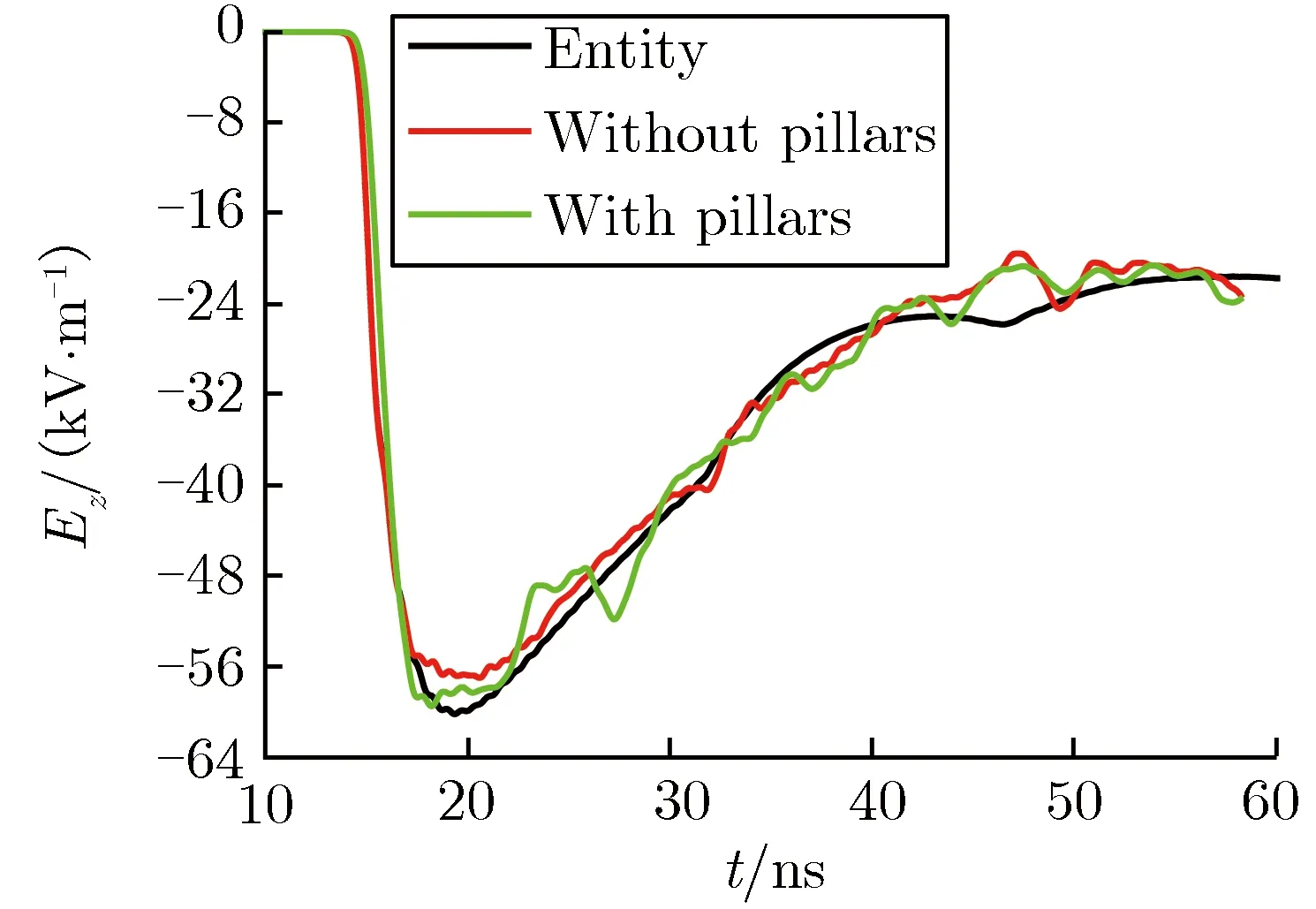
(c)B (2.828 m, 2.828 m, 0 m) (d)B′(2.828 m, 2.828 m, 0.2 m)图10有、无介质支撑圆柱时的电场强度时域波形对比Fig.10Comparison of electric field strength in time-domain with or without pillars

3.6加载电阻对辐射场的影响

设实体圆锥的高度Hc为1.1 m，线栅半径rd为2.5 mm，线栅数目Nt为24。从z0=3.126 m的位置开始沿着z方向向上加载3层分布式电阻，图11为电阻加载示意图。设电阻的长度为12 cm，相邻电阻之间的间距为24.5 cm。每层离散加载的总电阻R(z)随加载位置z的变化关系为[28]

R(z)=R(z0)eγ(z-z0)

(4)

其中，R(z0)为开始加电阻的z=z0层的总电阻；γ为常数，γ=0为均匀加载。根据3.5节的分析，为避开2个介质支撑圆柱对测点电场强度峰值附近的叠加干扰，选取位于介质支撑圆柱对角线延长线上且与模拟器中轴线的距离rz=2.5 m的测点C(1.767 m, 1.767 m, 0 m)，C′(1.767 m, 1.767 m, 0.2 m)及rz=4 m的测点B(2.828 m, 2.828 m, 0 m)，B′(2.828 m, 2.828 m, 0.2 m)进行模拟。

图11电阻加载示意图Fig.11Configuration of wire simulator withthree-rows resistors

设γ=1.03，模拟得到R(z0)取不同值、且与模拟器中轴线的距离rz为2.5， 4 m的各测点的电场强度峰值、上升沿和半高宽，如表5所列，各测点的电场强度时域波形，如图12所示。

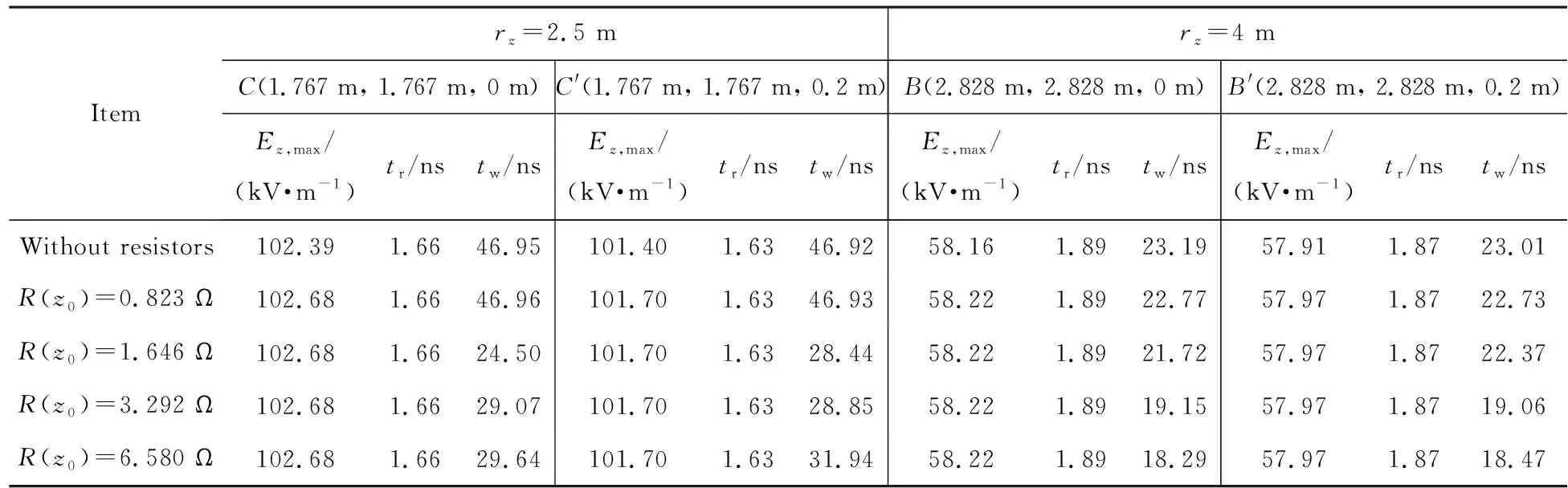
表5有、无电阻加载时的电场强度峰值、上升沿和半高宽Tab.5Comparison of the peak-value, rise-time, and FWHM of electric field strength with or without resistors

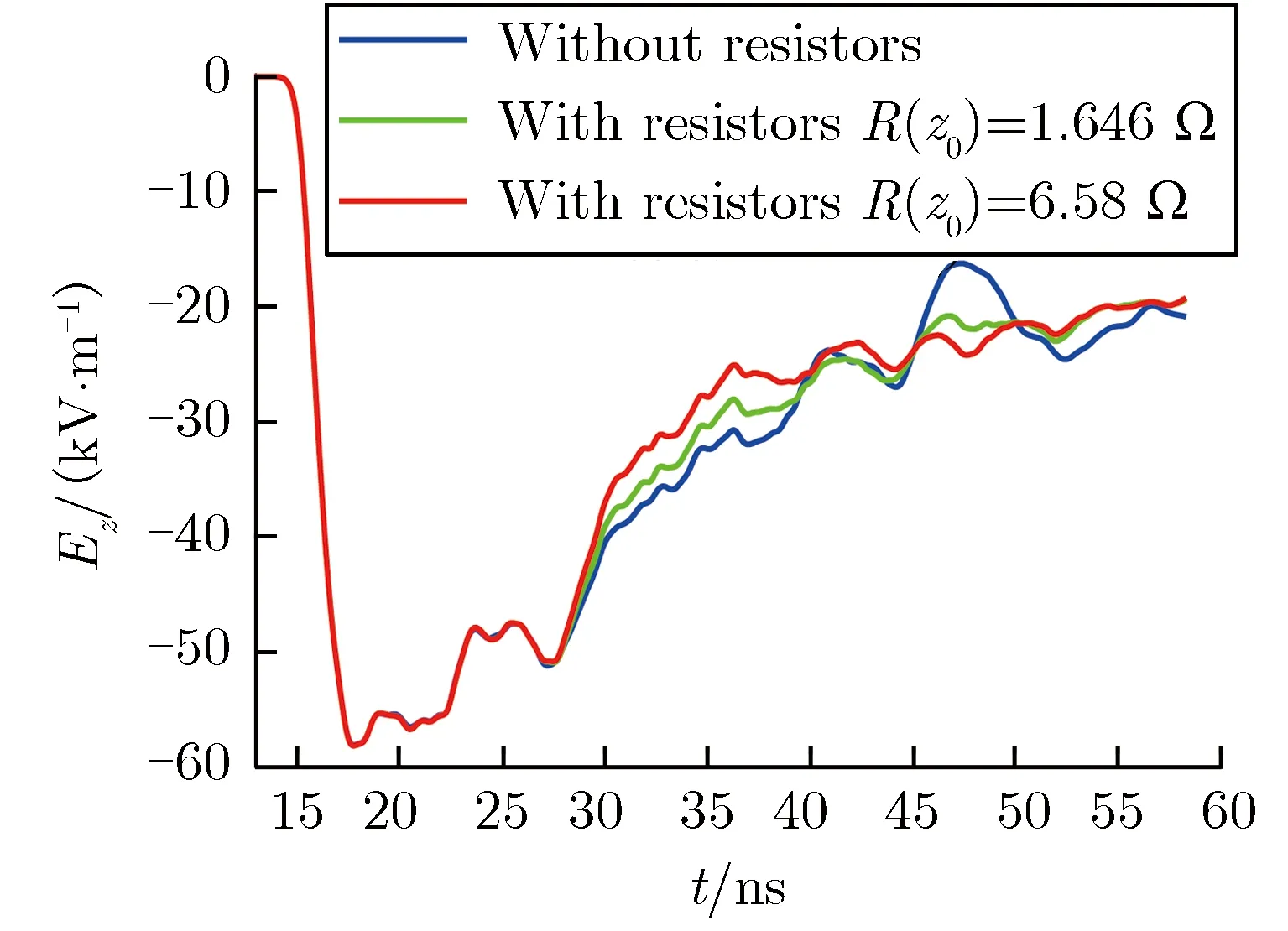
(c)B(2.828 m, 2.828 m, 0 m) (d)B′(2.828 m, 2.828 m, 0.2 m)图12有、无电阻加载时的电场强度时域波形对比Fig.12Comparison of electric field strength in time-domain with different resistor loads

为方便比较，表5和图12还给出了无电阻加载时的模拟结果。由表5和图12可见，与无电阻加载的情形相比，对模拟器进行电阻加载，会使所选测点的电场强度时域波形发生改变，且波形开始出现改变的时刻与电阻对测点的最短光程相对应。与无电阻加载情形相比，当R(z0)分别为1.646，3.292，6.580 Ω时，所选择的4个测点电场强度时域波形半高宽均变窄。这是由于电阻对流过线栅上电流的损耗，导致天线辐射性能下降的缘故。当R(z0)为1.646 Ω时，电阻加载对距离中轴线2.5 m的C点和C′点的电场强度时域波形半高宽的抑制效果最好。此时，与无电阻加载情形相比，电阻加载使得测点的半高宽变窄，满足(23±5) ns技术指标要求的区域范围增大。建议模拟器设计时，可通过加载电阻的方式增加有效测试区域。

4结论

本文介绍了基于PMC镜像法的同轴馈电模拟器辐射场并行FDTD计算方法，并对高度为4 m的线栅型垂直极化EMP辐射波模拟器的辐射场特性进行了研究，得到了模拟器的各类结构参数、支撑圆柱结构及电阻加载对辐射场的影响。结果表明，模拟器设计时应尽量选择一截线栅模型及较高的底部金属实体圆锥；实验时的验收点可以选择在支撑圆柱对角线的延长线上；采用电阻加载方式，可以增加模拟器的有效测试区域。本文模拟方法具有通用性，相关结论可为垂直极化EMP辐射波模拟器的设计和架设提供参考。