脉冲X射线辐照铝板气化反冲仿真的不确定度量化方法

王 栋，汤文辉†，张 昆，冉宪文，晏 良

(1.国防科技大学物理系，长沙410073；2.国防科技大学体系科学系，长沙410073)

在纳秒级极短脉冲宽度内，高能注量X射线辐照会导致材料比内能急剧升高，材料迎光面气化，由此产生的热压分布和气化反冲冲量(blow-off impulse,BOI)在材料内形成激波，对航天器和导弹等防护材料造成毁伤[1]。

对于脉冲X射线辐照诱导的BOI热-力学效应，国内外从20世纪就开展了大量的理论求解和实验研究。在理论求解方面，推导了一系列的解析计算公式，如BBAY公式[2]、Whitener公式[3]、MBBAY公式[4]及 Zhang公式[5]等。这些公式都基于一定的假设和简化处理，主要用于快速估算。在实验研究方面，美国国家实验室建设了SATURN、DOUBLE EAGLE等高能注量X射线源，并开展了一系列实验；我国在“强光一号”上开展了软X射线辐照实验。但上述X射线源实验成本很高，且辐照靶材较小，对结构响应研究具有局限性。此外，我国还开展了一系列炸药加载、柔爆索加载、电子束和离子束加载等模拟加载实验[7-10]，但是不可避免地在实验等效性上存在误差。

数值仿真技术弥补了X射线源实验条件的不足，与理论解相比，可以利用更精细的计算模型和复杂的初、边界条件，借助超算进行大尺度仿真，发挥建模灵活性及数据采集与参数优化等方面的优势。美国空军实验室开发的1维仿真程序PUFF-TFT[11]，考虑了次级粒子输运引起的剂量增强效应，更精确地描述了X射线的能量沉积过程，主要用于评估X射线沉积导致的1维应变-应力响应和薄层叠加效应。美国圣地亚国家实验室开发了CTH程序，用于建模仿真大形变和高强度冲击下的3维复杂响应问题[12]，包括黏塑性和率相关模型，实现了自适应网格细化和大规模并行计算，有效提高了计算精度和计算效率。汤文辉等采用光滑粒子流体动力学方法对金属铝在脉冲X射线辐照下的BOI进行了数值模拟[13]。蒋邦海研究了某种纤维增强型复合材料的1维应变率相关动态本构模型，用于1维X射线辐照动力学的数值模拟[14]。黄霞等建立了2维正交各向异性动态弹塑性本构模型，基于有限元法开发了2维仿真程序TSHOCK2D[15]，对碳酚醛材料中的2维X射线热击波和BOI进行了研究。ZHANG等将各向异性本构模型推广到3维，并在文献[15]的基础上开发了3维仿真程序TSHOCK3D[16]。这些仿真程序，缺少动态内存分配、动态时间步及自适应网格技术等计算优化方法，如采用高精度网格，仿真计算将耗时较大。

在对脉冲X射线辐照动力学过程的建模与模拟中，由于存在模型及材料物性参数测量不确定度等情况，仿真输入参数中存在随机不确定性和认知不确定性，通过计算模型的传导，导致材料响应和结构响应的估计结果的不确定性，最终会导致气化反冲仿真结果的不确定性，对数值仿真结果的可靠性或可信度评估带来挑战。如何量化数值仿真中由于输入参数不确定性导致的响应量的不确定性是一个值得探讨的问题。

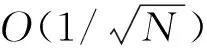
针对MC方法收敛性低的问题，一种解决方法是使用拟(MC)方法，该方法的不确定度近似为O(1/N)量级，但仍有一定的局限性；另一种解决方法是用代理模型(也称元模型)，近似原仿真模型，可显著减少计算时间。现有的代理模型众多，如响应面法、径向基函数法及样条插值法等[19]。与其他方法相比，Kriging代理模型具有回归和插值的双重特性及良好的非线性估计性能，能给出预测点处的估计方差，对开展不确定量化和模型精度评估具有一定优势，应用较广。

但是，本文仿真的高精度样本较为稀缺，计算耗时仅能承受个位次数的仿真，不足以构造足够精确的Kriging模型来解决12维的问题。因此，本文通过网格收敛性分析，选取一组具有均衡时效比的低精度网格来获取低精度样本，将高、低精度样本通过训练Co-Kriging模型进行数据融合，有效解决了数值仿真样本点获取成本较高带来的代理模型精度较低，甚至无法建立代理模型的问题；同时，提出了一种基于留一法交叉验证的序贯试验设计方法，提高了采样效率，确保了代理模型精度；最后，基于TSHOCK3D实现了X射线辐照铝板气化反冲仿真，并进行了不确定度量化分析。

1BOI的有限元仿真

X射线的辐射功率通常采用Planck黑体辐射模型：

(1)

其中，c1，c2分别为第一、第二辐射常量；λ为波长；T为黑体温度。在数值上，将λ离散，并截断上下限。归一化处理后，对于波长处于Δλi内的光子，能量占入射能量的份额ωi(λ)为

(2)

X射线能量沉积计算中主要考虑光电效应和Compton散射效应。查表可得Δλi内铝对光子的质量吸收系数μi(λ)。假定X射线脉冲波形是矩形波，在1维条件下，X射线能注量Φ(x)在材料内随入射深度x的变化关系为

(3)

其中，n为离散个数；ρ0为材料的初始密度；Φ0为初始入射能通量。对于3维条件下的能量沉积计算，采用矢量面积分方法进行简化计算[20]。

BOI的数值计算方法有2种。一种是通过计算迎光面处的压力对时间积分获得；另一种是通过计算气化单元的动量之和获得。文献研究认为，气化单元尺寸的急剧膨胀，使得单元两端节点处的速度和密度差较大，进而导致数值计算结果的不确定度增加[21]。因此采用第一种方法计算更为准确。

更新拉格朗日方法的控制方程组为

(5)

采用弹塑性流体力学本构，塑性屈服采用von-Mises屈服准则，断裂采用最大拉应力准则，物态方程采用修正的各向异性PUFF物态方程[22]。

2不确定度量化方法

近年来，不确定性量化理论快速发展，但目前还没有统一、标准的数学框架。基于样本的不确定性量化分析有4个基本步骤[23]：1)通过抽象物理模型，构造数学模型和计算模型，建立输入变量x和目标响应量y的数值映射关系；2)根据专家经验或统计数据，利用概率密度分布函数描述输入变量x的认知不确定度或随机不确定度；3)从输入变量x到目标响应量y进行不确定度传递；4)给出不确定性分析结果，如目标响应量的经验概率密度分布。此分析过程一般利用MC方法，通过对随机输入参数进行概率抽样和确定性仿真，完成不确度传递，并对目标响应量y进行概率统计分析。

本文基于样本的不确定性量化分析框架，对不确定度量化过程进行细化和改进，利用Co-Kriging代理模型来融合两类仿真精度数据点，进行MC仿真，不确定度量化流程如图1所示。

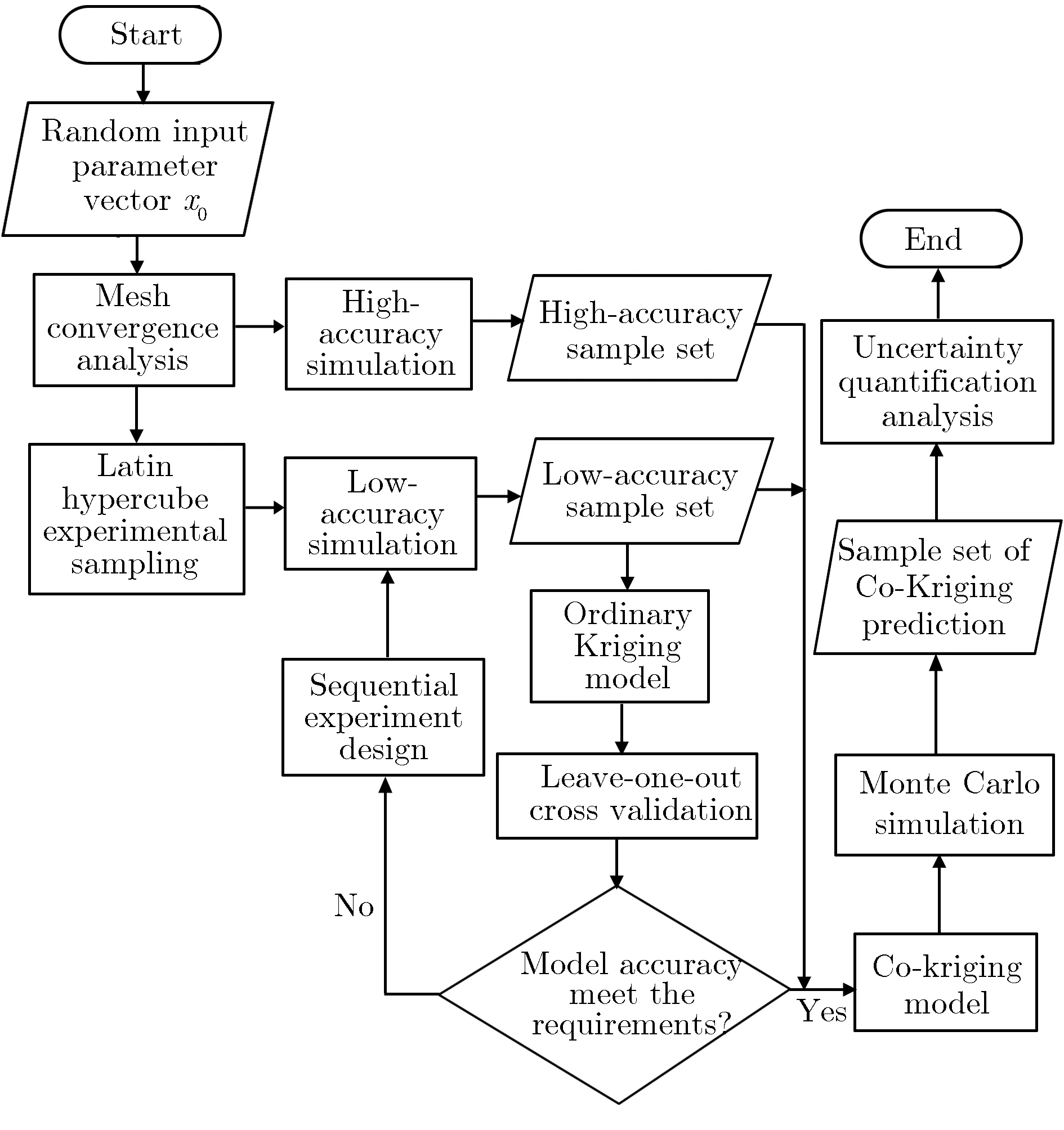
图1不确定度量化流程图Fig.1Flow chart of uncertainty quantification

2.1Kriging模型的构造

常见的Kriging代理模型有Simple Kriging (SK) 模型，Ordinary Kriging (OK) 模型，Universal Kriging (UK) 模型和Blind Kriging (BK) 模型，主要差异在于假设的回归函数的形式不同。选择回归函数是Kriging建模的难点，目前主要通过经验或试算来选择。工程问题一般假设回归函数为常数，采用OK模型。对于UK模型，基函数选择不当会降低代理模型的估计精度。BK模型通过一种贝叶斯特征选择技术，从基函数备选集中选择有显著影响的基函数加入回归函数中，需要利用更多的样本点进行训练，但其在某些测试函数中的性能与OK模型接近[24]。因此，对于计算参数维度高及非线性程度高的工程问题，综合考虑计算时间和拟合精度，OK模型是较优的选择[25]。但是，对于样本点抽样困难的情况，OK模型的预测精度较差。O’Hagan等将Co-Kriging (CK) 模型引入工程仿真计算领域，利用易抽样的低可信度样本来辅助抽样困难的高可信度样本构建代理模型，提高了模型整体预测精度[26]。

综上，由于本问题的高精度仿真计算时间较长，本文构造具有较高保真度的代理模型予以解决。首先，采用拉丁超立方设计，计算得到一定数量的高精度仿真样本；其次，基于OK模型进行序贯试验设计，计算得到低精度仿真样本；最后，基于CK模型融合不同精度的仿真样本，实现代理模型构造效率和全局预测精度的平衡。

给定样本集X={x1,x2,…，xn}，x∈d对应的响应量集记为y={y1,y2,…，yn}，y∈,输入输出样本的维数分别是d维和1维，样本数为n。为了消除量纲的影响，提高Kriging模型的精度和鲁棒性，对样本集和响应量集进行归一化预处理。

通常，Kriging模型包含插值和回归两重属性，其构造包括2步，首先基于样本集构造回归函数(趋势函数)，然后基于残差构造高斯过程Z(x)。OK模型假设回归函数为常数，可以写为如下形式：

Y(x)=μ+Z(x)

(6)

其中，μ为常值回归函数；Z(x)为高斯过程函数，满足下面统计学特征：

其中，R(Θ,x,x′)为任意两个样本点x和x′之间的相关函数模型，包含一组超参数Θ={θ1,θ2，…,θn}。对工程类问题，Matérn相关函数具有更好的拟合效果[27]，这里采用Matérn32相关函数，其形式为

(8)

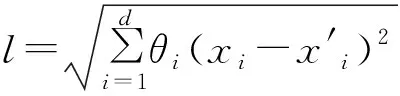
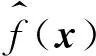
(10)

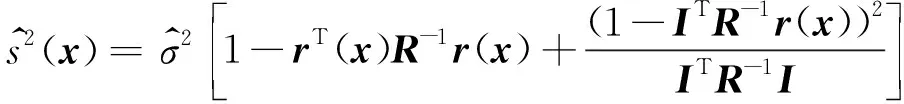
其中，r(x)是n维向量,第i个元素是待估样本点x和已知样本点x(i)的相关函数R(Θ,x,x(i))。

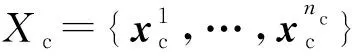
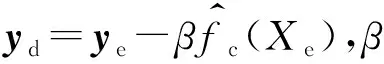
(12)

(13)

(14)

其中，(σc,rc,Rc)和(σd,rd,Rd)分别由OK模型Yc(x)和Yd(x)进行极大似然估计得到；回归系数β从Yd(x)的极大似然估计中获得。

2.2序贯试验设计

Kriging代理模型的预测精度很大程度上取决于训练集的数量。通过试验设计可以用尽量少的试验点得到尽可能多的模型信息，从而高效地构建Kriging模型。Kriging模型通常配合拉丁超立方抽样(Latin hypercube sampling, LHS)，用一次性采样点集训练Kriging模型。但是一次性采样会造成样本点的冗余或不足，导致计算资源浪费或达不到要求的代理模型精度。

序贯设计(sequential design, SD)可以有效解决上述问题。其基本思想是用一组数量较少的初始训练样本点为基础，根据已有样本点信息和已构造的近似模型信息对精确模型的定义域进行序贯采样，有针对性地补充精确模型信息，以逐步提高近似模型的全局或局部预测精度，直到满足预设要求的精度[28]。序贯试验设计的核心是根据试验设计目标，选择合适的序贯加点准则，本质上是利用某个目标函数来衡量新样本点对模型精度的改善，将样本点的选取问题转化为最优化问题。重复上述过程直到满足终止条件停止采样。

本文使用应用较广的“最大方差”加点准则[29]，最大程度减小Kriging模型的全局预测方差，选择参数空间内使得预测方差s2(x)最大的点xnew作为下一个采样点：

(15)

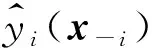
(16)

在实际计算中，随着样本点增多，LOOCV方法带来的开销逐步增大。文献[31]提出了一种近似计算公式，在留一交叉验证时保持训练样本集不变，大大提高了计算效率。近似计算公式为

(17)

其中，Hi,:,H:,i分别代表矩阵的第i行和第i列元素，Hii代表对角线上元素。

最后，当σCVPE的连续相对改善(successive relative improvement, SRI)σSRI低于某个阈值时，采样终止。σSRI的定义为

(18)

综上，本文提出的序贯试验设计算法如下：

Step 1：对于d维输入参数，基于最大化最小距离准则进行初始LHS抽样n0=2d+1个点，并对样本点进行仿真，得到初始样本集X(n0)和响应量集Y(n0)。

Step 2：训练OK模型，计算初始σCVPE(n0)。

Step 3：选择xnew作为下次仿真计算样本点xn0+1，更新OK模型，并计算σCVPE(n0+1)。

Step 4：计算连续相对改善σSRI(n0)。若样本数n≤nmin，回到Step3。

Step 5：若σSRI(n0)连续4次低于阈值σ0，则停止。否则回到Step3。

需要注意的是，为防止前期σSRI的偶然性波动，需设定一个最低迭代次数nmin=4d。

序贯试验设计流程如图2所示。

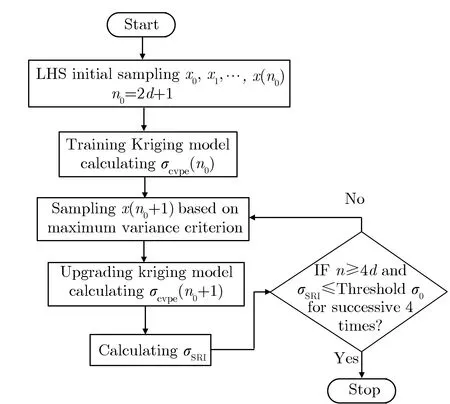
图2序贯试验设计流程图Fig.2Flow chart of sequential experiment design

3算例与分析

利用有限元程序TSHOCK3D进行算例仿真和结果分析，使用Ansys前处理生成正交六面体单元网格，并且假设X射线垂直靶面入射，有限元网格划分以及仿真场景，如图3所示。

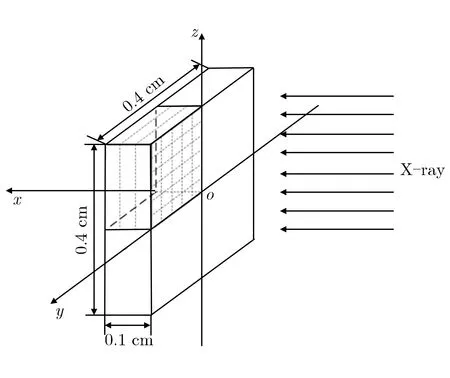
图3有限元网格划分以及仿真场景示意图Fig.3Schematic diagram of finite element griddivision and simulation scene

3.1输入参数不确定度分布

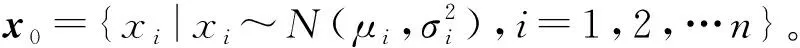
关于输入参数的不确定度分布，本文仅根据专家经验给出粗略估计。对于铝的10个物性参数，采用3σ准则给出标准偏差的估计，出于简化问题考虑，取3σi=0.1μi，即假设各参数以99.73%的概率落在μi±3σi区间内。对与辐射源有关的X射线复合谱及能注量，则基于实际X射线复合谱及能注量的等效简化假设选取值，并根据专家经验假设正态分布，根据3σi=0.1μi给出标准偏差的估计。

针对这一组参数x0开展气化反冲仿真的不确定度量化，具体各参数的取值及不确定度分布按上述估计给出，如表1所列。

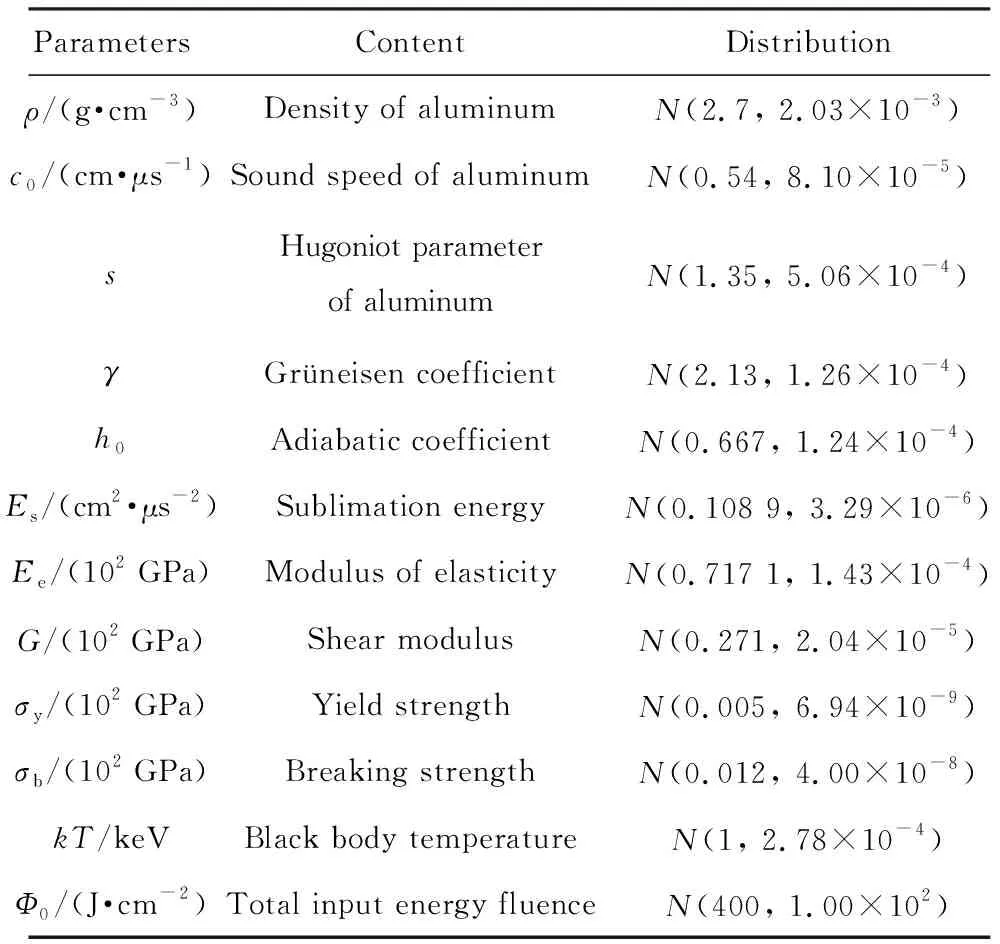
表1各参数的取值及不确定度分布Tab.1The distribution of random parameters

3.2网格收敛性分析

进行网格收敛性分析，一是选择1组高精度网格，近似地满足计算网格无关性条件；二是选择1组合适的低精度网格来开展多精度数据的融合，在代理模型精度和样本计算开销上寻求平衡。算例在0.1 m×0.2 m×0.2 m的靶板区域内进行仿真，考虑到对称性边界只计算1/4模型。为避免边侧稀疏波的干扰，y，z方向长度为x方向长度的4倍。取靶板迎光面和x轴交汇点(原点O)为应力监测点，对时间积分得到BOI。采用中间加密法细化网格，对得到的各组网格进行仿真，给出铝板BOI随网格数量变化关系，即铝板BOI的收敛性曲线，如图4所示。

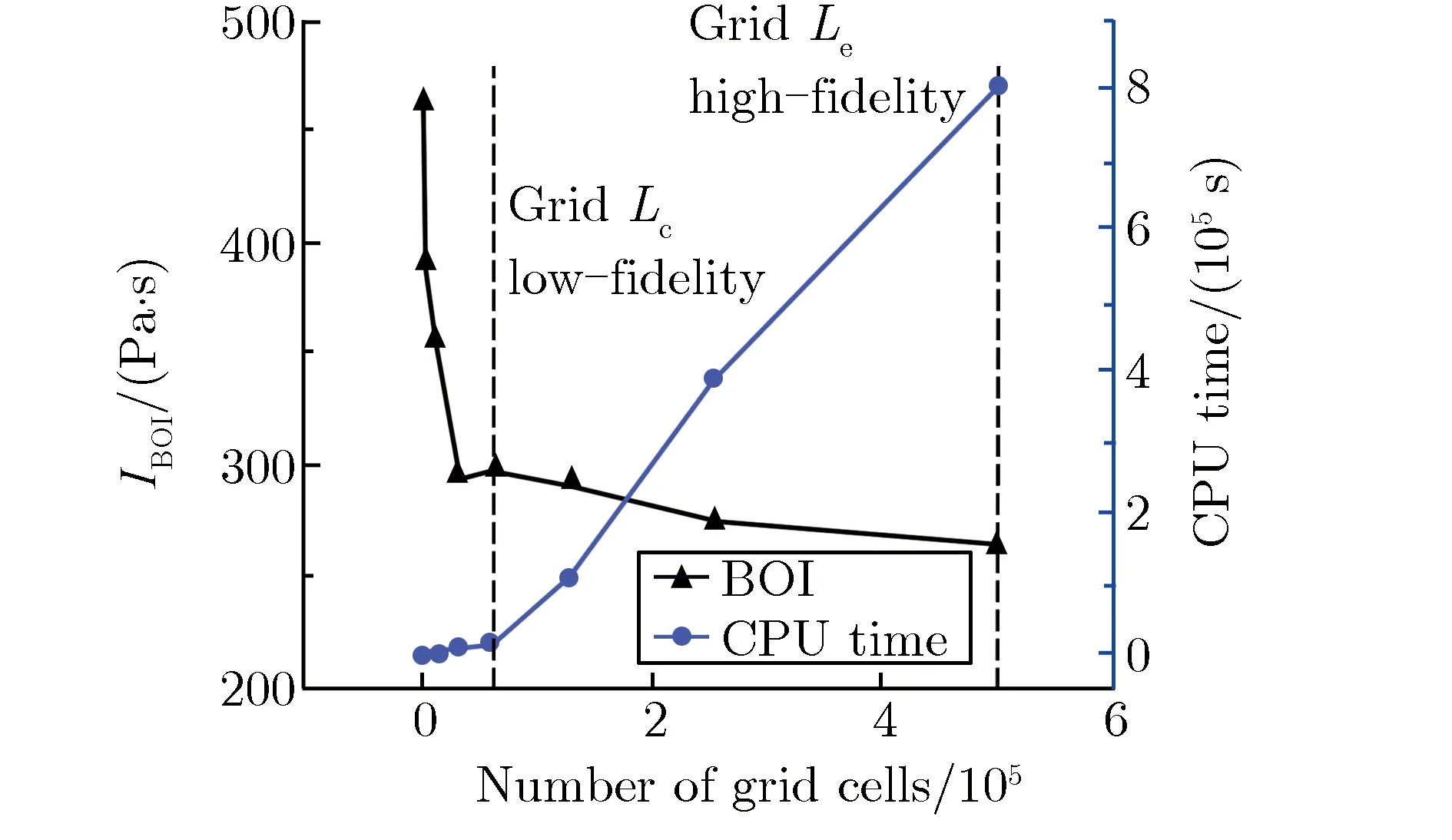
图4铝板BOI的网格收敛性曲线Fig.4Grid convergence curve of blow-off impulse

由图4可见，随着网格密度增加，CPU计算时长快速增加，BOI逐渐收敛。原因是软X射线的能量沉积曲线在迎光面附近急剧下降，x方向网格精度极大地影响了能量沉积离散的计算精度。随着网格精度的提高，离散单元的能量沉积逐渐收敛，最终与连续能量沉积曲线对应。由于程序采用均匀网格，提高网格精度将带来CPU计算时长的增加，降低边际效益。因此，综合考虑时效比，对照网格收敛性曲线，选定BOI收敛速度趋缓处对应网格作为低精度网格，记作Lc。将BOI基本达到收敛处对应网格作为高精度网格，记作Le。取产生BOI的时刻为0时刻，对比两类网格仿真的BOI随时间的变化关系，如图5所示。

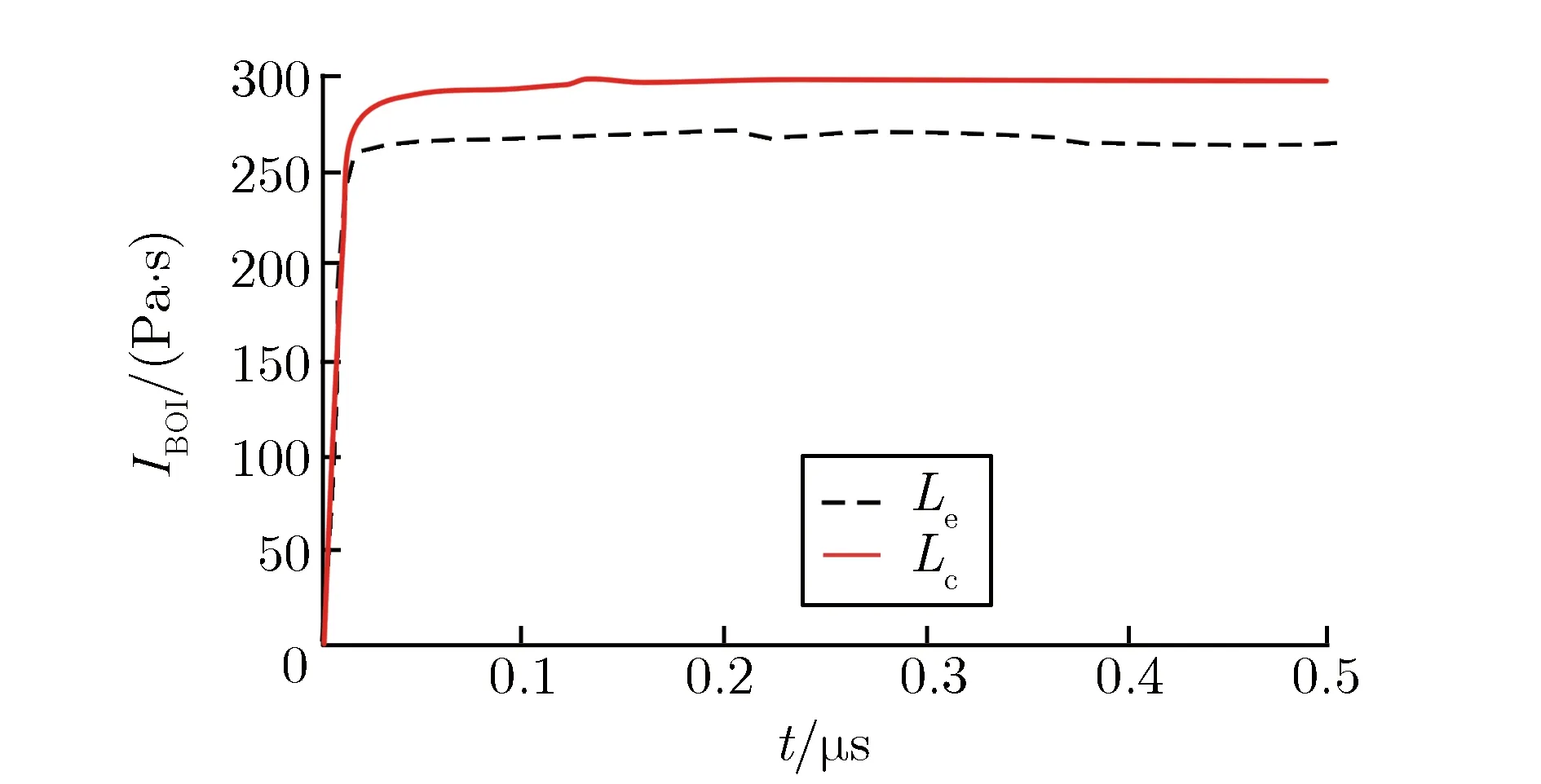
图5采用Le和Lc精度网格的铝板BOI随时间的变化关系Fig.5Comparation of Le and Lc grid simulationof blow-off impulse induced by pulsedX-ray irraditation on aluminum

3.3序贯试验设计和CK建模

在高精度样本集的选取上，基于最大化最小距离准则对随机参数向量x0进行一次性的LHS采样。由于计算耗时的限制，设计6个样本点进行Le精度仿真。在低精度样本集的选取上，采用基于最大化最小距离准则的LHS设计初始25个样本点，并进行Lc精度仿真。选择t=0.5 μs时刻(平台期)的BOI作为响应量，训练初始OK模型，按照序贯采样算法继续采样92次，直至达到停止条件。此时，迭代训练后的OK模型σCVPE=0.003 4。σSRI的收敛趋势如图6所示。

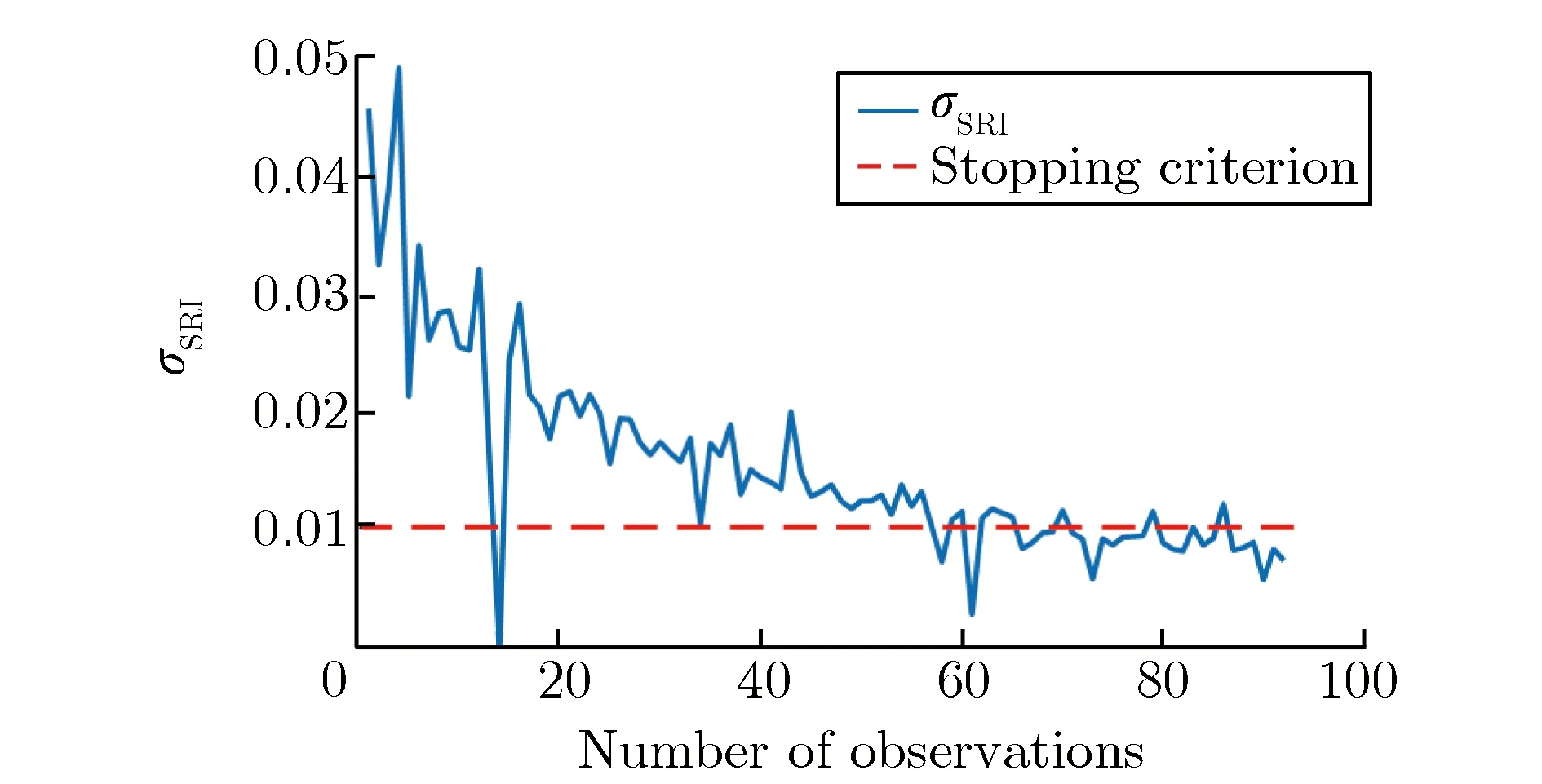
图6Lc精度网格仿真σSRI收敛趋势图Fig.6Convergence trend of Lc grid simulation

用117个Lc精度仿真结果和6个Le精度仿真结果中t=0.5 μs时刻的BOI作为响应量，训练得到CK-1模型，相应σCVPE=0.009 3。同时，选择t=0.05 μs时刻(上升期)的BOI作为响应量，训练得到t=0.05 μs时刻的CK-2模型，相应σCVPE=0.009 0，可以看到CK-2具有与CK-1接近的模型预测精度。

3.4响应量BOI的不确定度量化

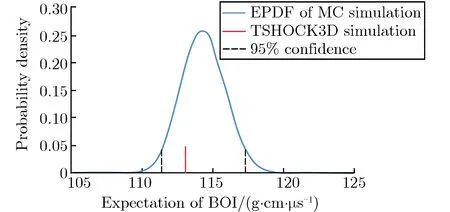
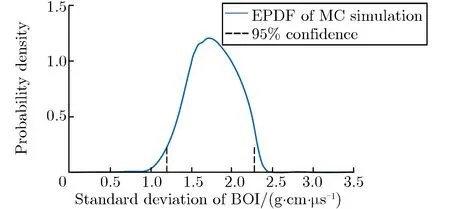
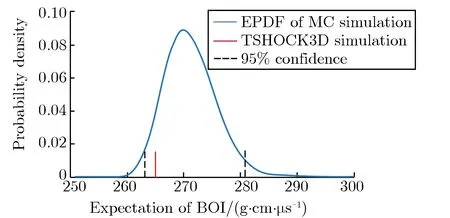
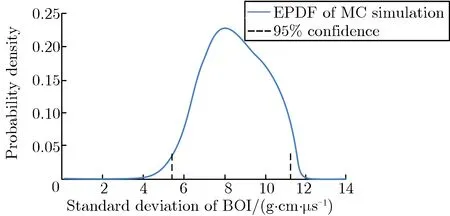
核密度估计 (kernel density estimation, KDE) 是在概率论中用来估计未知参数的密度函数，属于非参数检验方法之一。基于已经获取的MC仿真样本，本文采用Epanechnikov核函数对响应量总体的概率密度进行估计，得到近似的概率密度函数，即经验概率密度函数 (empirical probability density function, EPDF)。利用上述两个时刻数据训练的CK-1和CK-2模型，分别进行MC仿真1×106次。分别对两个时刻的样本点集进行核密度估计，得到t=0.5 μs和t=0.05 μs时刻的BOI的期望和标准差的经验概率密度函数及其95%置信区间，如图7所示。

(a)t=0.05 μs

(b)t=0.05 μs

(c)t=0.5 μs

(d)t=0.5 μs

由图7可见，在t=0.05 μs时刻，根据MC仿真得到BOI的95%置信区间为111.40～117.29 g·cm·μs-1，实际Le精度仿真结果Ie=113.07 g·cm·μs-1落在95%置信区间内。在t=0.5 μs时刻，根据MC仿真得到BOI的95%置信区间为263.29～280.94 g·cm·μs-1，实际Le精度仿真结果Ie=265.04 g·cm·μs-1落在95%置信区间内。因此，认为以高精度网格Le采用输入参数组x0仿真得到的BOI在5%显著性水平下是可信的。

此外，基于建立的CK模型，还可实现±10%参数空间内的BOI的快速预估。下面重新设计6组样本点，对比Le精度仿真结果和CK模型预测结果。其中，前6组用CK-1模型进行估计，后6组用CK-2模型进行估计。对比TSHOCK3D仿真结果，预测的平均相对偏差在5%以下，如表2所示。

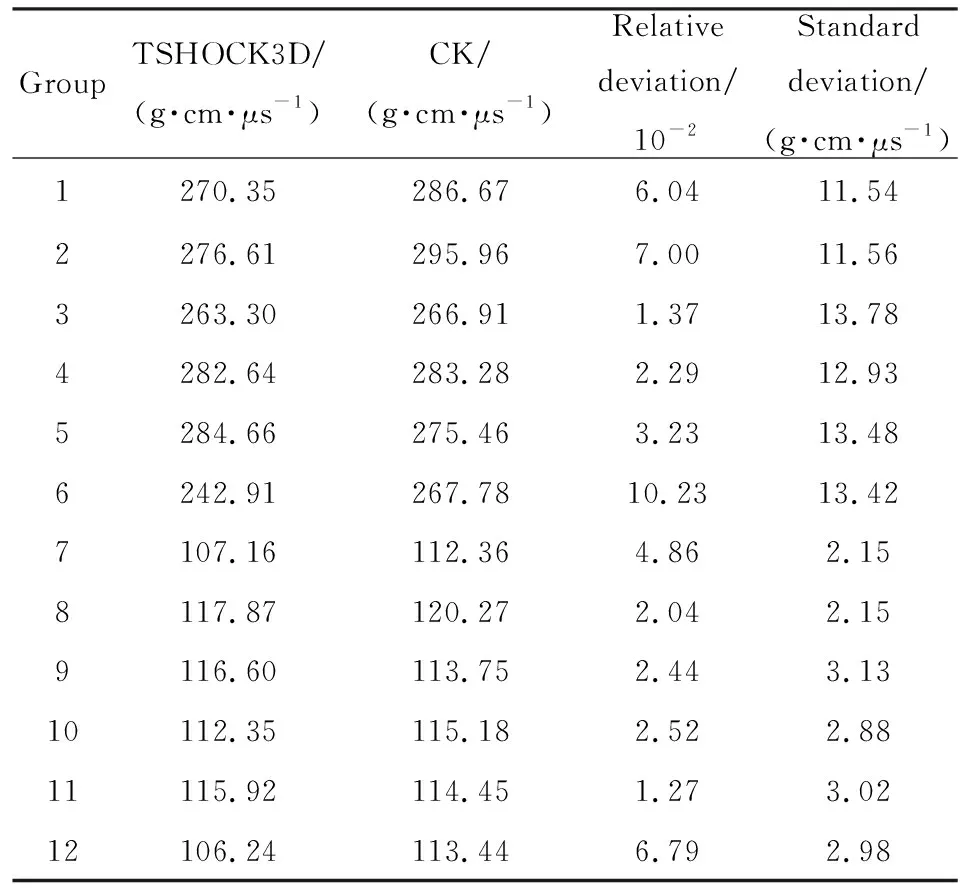
表2CK模型对BOI的快速评估及相对偏差Tab.2CK model fast prediction for BOI and its relative error

4结论

1)针对脉冲X射线辐照铝靶BOI数值仿真输入参数的不确定性问题，本文提出了一种改进的MC不确定度量化方法。通过加入序贯试验设计采集样本，及采用CK模型进行数据融合，有效提高了不确定度量化的效率。给出了1 keV软X射线脉冲辐照下铝板BOI仿真结果的经验概率密度分布及其95%置信区间。计算结果表明，基于高精度网格的仿真结果在5%显著性水平下是可信的。

2)通过新的高精度仿真样本验证，本文建立的Kriging代理模型，平均估计相对偏差在5%以下，可用于x0(1±10%)参数空间内的BOI的快速预估。

3)下一步将根据相关实验或数值计算及其他不确定度信息，更准确地给出分布参数的估计。同时，基于建立的Kriging模型进行输入参数的敏感性分析，如采用Sobol法给出对仿真结果影响较大的输入参数。