差分遗传算法优化BP神经网络的双目相机标定

张峰峰，陈龙，薛保珊，闫晓剑，孙立宁

(1.苏州大学 机电工程学院，江苏 苏州 215006；2.苏州大学 苏州纳米科技协同创新中心，江苏 苏州 215123)

近年来，双目立体视觉在机械制造、定位、测距以及三维重建等领域有着越来越广泛的应用，相比于单目立体相机，它能够获取更多目标深度信息[1-3]。双目立体视觉主要利用视差原理对从不同位置获取的2幅图像上的同名点之间的位置偏差进行计算，从而获得目标物体的三维信息[4]。双目相机的标定是基于双目立体视觉进行三维重建、视觉检测等研究的重要环节，因此自动、高精度的双目相机标定是实现高精度双目视觉三维重建、定位等功能的重要前提[5-7]。

双目相机的标定决定了双目立体视觉成像系统的内、外部参数，相比于单目立体相机，其标定过程比较繁琐，对算法优化和目标变化的要求更高[8-9]。目前所存在的双目相机标定方法大多依赖于精确的成像数学模型，对成像过程中各种非线性畸变因素考虑较少。人工神经网络是人工智能领域近年来发展起来的一种新技术，它具有很强的自适应、自学习以及强大的非线性映射能力[10]。在双目相机标定过程中，相比于传统的相机标定方法，它无需确定相机的内部和外部参数，也无需了解相关的相机的成像模型，直接建立二维的相机像素坐标与物体的三维真实世界坐标的映射关系，并且将所有的非线性因素都包含在神经网络中，作为一种隐式标定。在使用人工神经网络算法对双目相机进行标定的研究中，使用BP神经网络算法较多，其在双目相机标定中的可行性已经被崔等人证实[11]。但是其标定精度和收敛速度在实际测试中并不令人满意。刘金颂等[12]提出了一种基于Zernike矩和粒子群(partical swarm optimization，PSO)算法的摄像机神经网络标定方法。该方法对BP神经网络进行优化，主要通过PSO算法优化BP网络的初始权重和阈值,提高网络的收敛速度和泛化能力。相比于普通的BP神经网络的双目相机标定其各方面能力都有了一定的改善，但是仍然不能满足实际工程中的需求。目前，大多数研究在应用BP神经网络进行双目相机标定主要面临的问题：左右相机图像中同名点的误匹配率高以及BP神经网络迭代时间较长、精度低、收敛性差。

基于以上情况，本文提出了一种差分遗传算法优化BP神经网络的双目相机的标定方法，克服了传统相机标定过程复杂、计算量大的问题。从而能够方便、灵活、高精度地对双目相机进行标定。

1 棋盘格角点的检测与自动匹配

1.1 基于能量生长算法的棋盘格的角点检测

棋盘格角点的检测是双目相机标定的重要环节之一，角点检测是为了获取棋盘格角点的像素坐标，因此角点检测的精度直接影响相机最终的标定精度[13]。采用基于能量生长算法的棋盘格角点检测具有鲁棒性好、角点提取精度高以及可以同时检测一个图片里包含多张棋盘等优点[14]。

首先，通过定义2种角点原型，一种类似于棋盘格中正方形的4个角，另一种为在第1种的基础之上，将正方形旋转45°的角点。每个原型由4个滤波核组成，用于后面和图像进行卷积操作。然后，利用这2个角点原型来计算每个像素点与角点的相似程度。对每个像素点都进行上述计算后，可以去掉大量的非棋盘格式的角点，同时得到所有可能的角点。其次，对上述角点的位置以及边缘方向进行亚像素级精细化处理。最后，给定一个种子角点，沿着其边缘方向搜索产生一个初始化的种子棋盘格。该棋盘格有3×3个角点，有2×2个棋盘。以此种子棋盘格为基础，分别从最外沿的4个边缘去生长棋盘格，生成4个新的棋盘格。如果其中能量最小的那个棋盘格的能量值比棋盘格扩展前的能量更减少了，就说明生长成功，用这个新的棋盘格代替原来棋盘格，继续生长，直到4个方向新棋盘格能量不再减少为止。

1.2 棋盘格的同名角点匹配

1.2.1 传统方法的同名角点匹配

传统的同名角点匹配主要在Opencv中通过Sift(scale invariant feature transform)、Surf(speeded up robust features)、Fast(features from accelerated segment test)等特征算子进行特征点检测[15-16]，再使用BruteForceMatcher或者是FlannBasedMatcher进行匹配。然后，经过一系列的错误匹配去除步骤获取优质的匹配结果。由于本研究标定块的6个面为类似国际象棋的棋盘，该棋盘的图案太过类似，从在同名角点匹配的时候，容易出现大量错误的匹配。常用于针对Sift、Surf、Fast等匹配行之有效的错误匹配点去除算法在这里效果较差。

1.2.2 基于光线扫描算法的同名角点匹配

根据光线投射算法的启发，本研究提出一种基于光线逐行扫描的同名角点匹配算法来克服棋盘格角点误匹配率高的缺点。基于光线扫描的同名角点匹配算法的原理图如图1所示，其主要分为以下几个步骤：

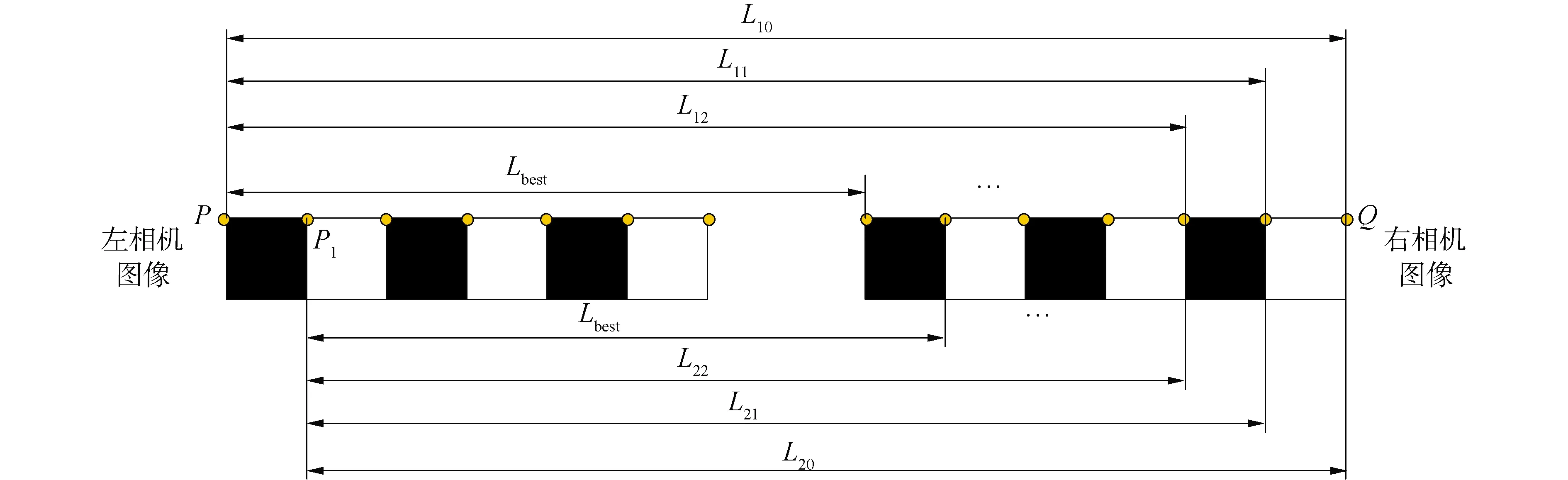
图1 基于光线扫描算法的同名角点匹配原理

1)通过Opencv中最小外接矩形的方法，搜寻与左摄像机拍摄的棋盘格图像的左上角最近的点，同时搜寻与右摄像机拍摄的棋盘图像的右上角最近的点，以此获取现有棋盘图像角点集合的左上角与右上角的2个点P、Q。

2)把棋盘的角点从上到下从左到右地划分，这样其实就获取了棋盘第1行的2个端点。将P、Q2点构造1条射线，通过计算左上角点到右上角点的方向矢量，将其作为射线方向。

3)保持P点静止，假设此时PQ距离为L10,将Q点从右往左逐步步进，不断计算PQ间的距离。当发现点Q处于剩余棋盘角点点集中的某一棋盘点与当前的P点处于的位置小于某个阈值(Lbest)时，将该点列为PQ射线经过的一个点。

4)把PQ射线经过的点存放到新的向量n1里，同时将这个点从剩余棋盘角点点集中去除。此时P点右移到P1的位置，然后将Q点继续从最右端角点开始进行下一次的步进。

依次类推，直到达到该行应该有的最大的同名角点匹配个数，那么这一行的同名角点匹配完成。其余棋盘图像各行同名角点匹配也是相同的步骤，只需要迭代棋盘的行数，比如9×9的棋盘迭代9次，就可以完成最终的同名角点的匹配。

2 差分遗传算法优化BP神经网络的双目相机标定

2.1 基于BP神经网络相机标定的参数设置

主要通过棋盘图像角点的二维像素坐标值作为BP神经网络的输入。利用BP网络自身固有的正向计算，反向优化权值的特点来进行棋盘图像角点的三维世界坐标的预测[21]。通过多组训练集对BP神经网络内部的权值进行不断训练和改变，拟合并建立二维像素坐标到三维世界坐标之间的关系。具体基于BP神经网络进行双目相机标定的结构示意图如图2所示。

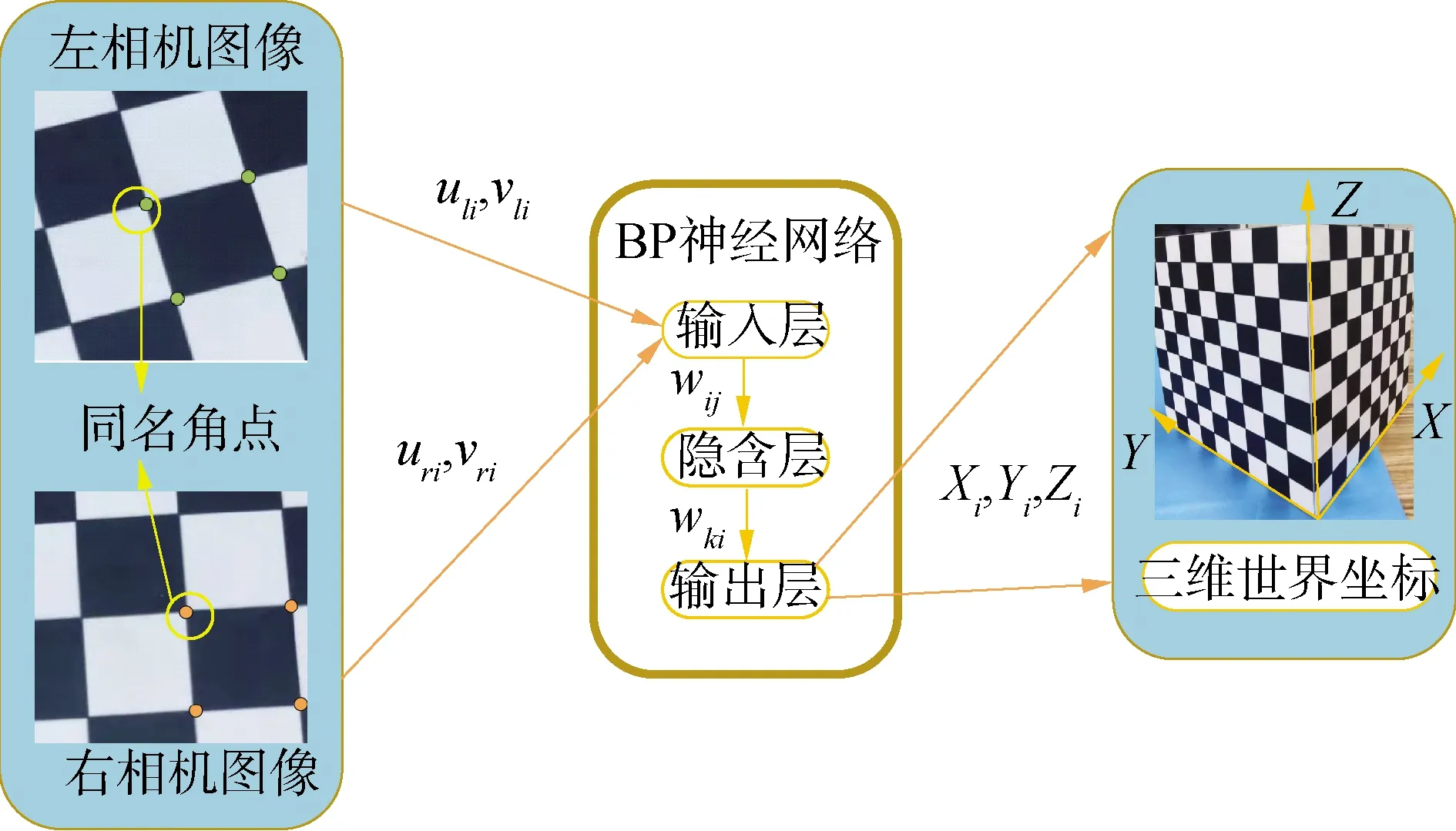
图2 采用BP神经网络的双目相机标定原理

2.2 差分遗传算法优化BP神经网络的双目相机标定原理

2.2.1 相机标定的数据种群适应性调节

传统的BP神经网络在进行双目相机标定时，容易陷入局部最优值，同时标定精度相对较低。引入差分算法后需要在前期开始差分进化的时候增强相机标定数据种群的多样性，在后期需要对最佳个体持续改善。因此，根据精英策略和适应度值来动态调节数据种群的规模对于双目相机的标定非常重要。根据：

(1)

GAVAPS[17]提出的双线性分配策略对大于种群设定的寿命的个体进行删除。式中：fmax和fa表示种群的最大和平均适应度；Mmax和Mmin表示寿命的最大、小值。

在删除部分个体的同时需要对数据种群多样性减少进行弥补。通过复制高适应度值的个体来增加种群规模，根据公式

Cn=ψ×(Nmax-NC)

(2)

NC+1=NC-ND+Cn

(3)

可以得到此时的种群规模的变化。式中：Cn表示复制个体的数目；ψ为复制的概率；Nmax代表了种群的最大规模；NC和ND分别表示当前种群规模和种群删除的个体的数目。

2.2.2 选择算子的改进

选择算子在双目相机标定的过程中起到重要的作用，主要以适应度函数作为参考，从相机标定的数据种群中挑选一些个体保留至下一代，剩下的个体全部淘汰，因此从相机标定的数据种群中选择的个体的好与坏将直接影响双目相机标定的后续操作。传统的选择算子在选择过程中误差较大，针对该问题，本研究利用排序法对其改进来减小选择个体之间的误差，第n个体在排序后被选择的概率Pnew重新定义：

(4)

Pnew=b(1-q0)β-1

(5)

式中：a表示种群的数量；b代表将q0标准化；q0作为最优个体被选择的概率；β表示第n个个体在整个种群排序后的位置。

2.2.3 交叉算子的改进

双目相机标定的数据种群的多样性主要依赖交叉概率[18]，同时遗传算法的全局寻优能力也受交叉概率的直接影响。在目前的研究中多数将其设定为一个常数值，在实际过程中最佳参数较难调节。本研究根据种群适应度的分散程度不同，将种群的最大和平均适应度即(fmax和fa)的关系定义为：

(6)

对交叉概率Qj的自适应性进行改进，x1表示自适应性参数为：

(7)

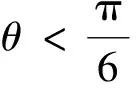
2.2.4 差分变异算子

双目相机标定过程中能否避开局部极值主要由遗传算法的变异概率决定[19]。与传统的遗传算法的变异算子不同，差分变异算子在相机数据种群整体的差异基础之上，种群个体之间的变异通过差分向量的形式对个体进行扰动来实现[20]。本研究对不同个体之间的向量差进行计算，同时引入待变异个体向量，对向量差采用缩放的方法与其合并成新的个体。具体的缩放合并公式为：

G(n+1)=Pr1(n)+ξ×[Pr2(n)-Pr3(n)]

(8)

式中：ξ代表向量差的缩放值；Pr1(n)代表待变异的个体的向量；Pr2(n)-Pr3(n)代表个体之间向量差。在实际的计算过程中需要根据适应度值的变化利用下式对ξ进行自动调节：

(9)

式中：Pw代表最差适应度值的向量；Pb代表最优适应度值的向量；χ表示适应度值调节参数。当适应度值较低时，此时需提高ξ值，以此来增加寻优解的概率，反之，则降低ξ值。

3 实验和结果

3.1 双目相机标定硬件平台的搭建

双目相机标定的硬件平台主要由图3所示的显示器、工作站、双目相机、标定块等组成。标定块为立方体，其6个面均布满相同数量的边长为1 cm的正方形。以图中所示立方体3个底边的角点作为原点O，并以3条棱作为X、Y、Z轴，便可以获取每个小正方形的角点的实际的三维坐标。

图3 双目相机标定的硬件平台

3.2 棋盘角点的检测和匹配实验

本文采用了基于能量生长算法来完成棋盘二维像素图像的角点检测，并且提出基于光线扫描算法来完成检测后的角点的匹配。在此基础上，本文利用双目相机拍摄如图4所示的图片，将拍摄的棋盘图像分成左、右相机图像，并且每次拍摄10～20张图片。利用本文提出的方法对分类好的左、右相机的图像进行角点检测和匹配，通过实验获得最终的效果如图5所示。

图4 双目相机拍摄的标定图像

图5 本研究方法的同名角点检测与匹配

为了验证本文提出的角点检测和匹配方法的稳定性，继续进行5组上述的实验，最终获得的同名角点匹配的正确率如表1所示。

表1 同名角点检测和匹配结果

结合图5和表1可以很清晰地看出采用本文提出的方法具有很高的同名角点匹配的正确率。为了进一步突出其在棋盘图像上应用的优越性，本文将其与传统的角点特征检测和匹配算法进行对比。例如分别采用Sift检测算法+FlannBasedMatcher匹配方法和Surf检测算法+FlannBasedMatcher匹配方法最终通过实验效果如图6所示，同名角点匹配的平均成功率如表示。从图6(a)中可以看出棋盘格对应点可以实现完美匹配，但是棋盘格的角点检测基本失效。从图6(b)可以看出该方法可以顺利实现棋盘格角点的检测，但是其同名角点出现多处匹配错误的问题。综合表可以看出采用本文的方法同名角点匹配成功率分别提高了90%和70%左右。

图6 基于传统方法的同名角点检测与匹配

表2 基于不同方法的同名角点检测和匹配结果

3.3 双目相机的标定实验和结果分析

3.3.1 不同方法的标定精度对比实验

利用本文提出的差分遗传算法优化后的BP神经网络来进行双目相机的标定，需要获得一定量数据的同名角点的二维像素坐标和对应的该点的三维世界坐标。将二维像素坐标作为神经网络的输入，三维世界坐标作为神经网络的输出。具体经过采集获得的部分的同名角点的像素坐标和三维实际坐标如表3所示。

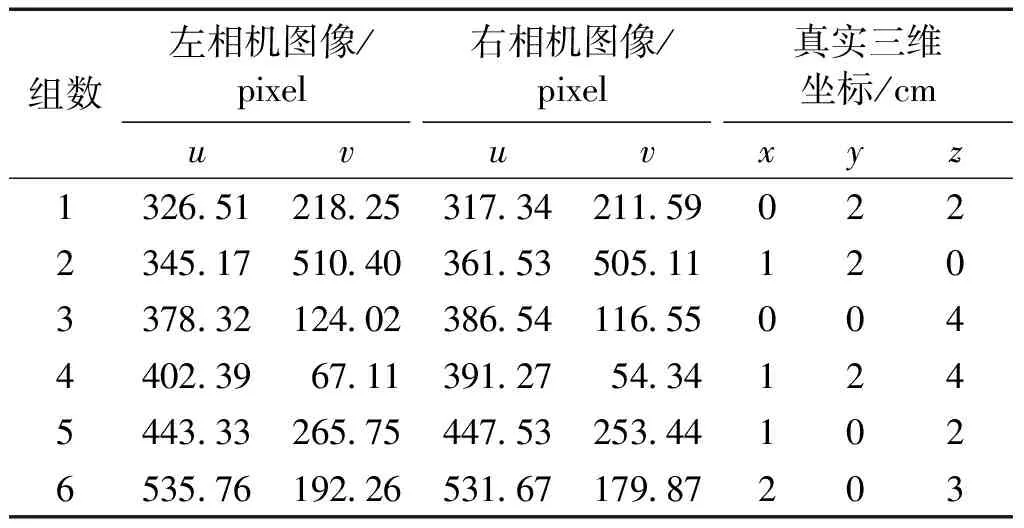
表3 同名角点的像素坐标和三维坐标(部分数据)

将类似表中500组同样的数据作为普通BP神经网络和本文提出的差分遗传算法优化后的神经网络的训练集。选取6组数据作为神经网络的测试集，通过实际的实验测试得出优化前后的神经网络预测角点的三维世界坐标的值分别如表4所示。

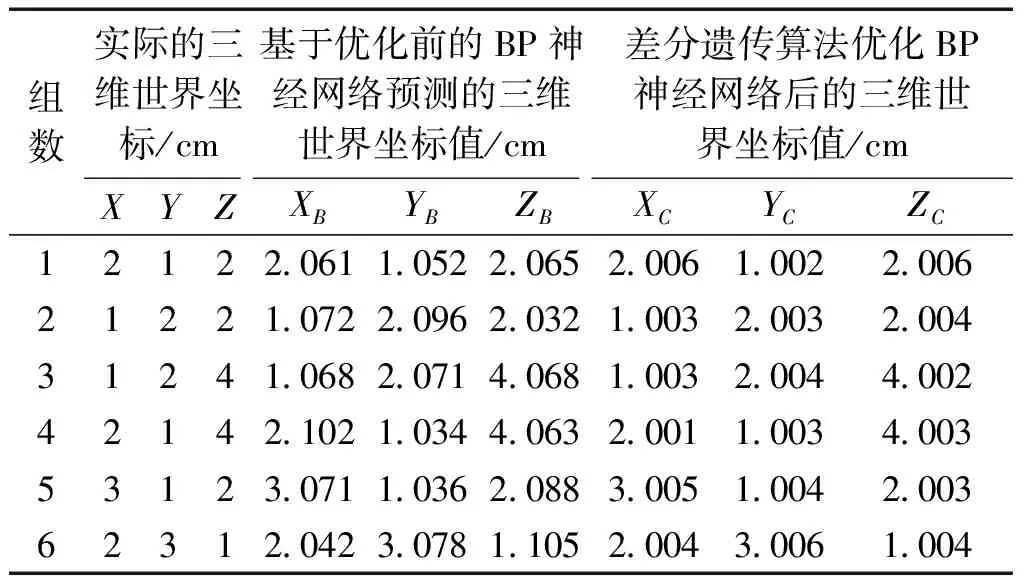
表4 神经网络预测角点的三维世界坐标值

为了进一步验证采用本文差分遗传算法优化后的神经网络来标定双目相机的精度，将其结果与采用Opencv的张正友标定和Matlab自带的双目相机标定工具箱标定出来的结果进行对比。利用基于Opencv的张正友标定方法对双目相机进行标定，需要大概10～20张双目相机的拍摄的图片。对拍摄的图片进行标定操作，便可以获得双目相机的内、外参数。在双目相机的内、外参数已知的情况下，便可以根据拍摄的棋盘的二维图像的角点像素坐标来计算出对应的三维世界坐标。与之相似的是，将拍摄的棋盘图像导入Matlab，利用自带的双目相机标定工具箱来标定出双目相机的内、外参。在标定出内、外参后，同样根据二维图像的角点像素坐标来计算出对应的三维世界坐标。

将神经网络标定的6组测试集的二维像素坐标，作为基于Opencv和Matlab标定的实验输入数据。通过各自标定出的双目相机的内、外参，分别计算出二者实际对应的棋盘角点的三维世界坐标。具体计算结果如表5所示。

表5 基于传统方法的角点的三维世界坐标值计算

3.3.2 标定精度结果的分析

采用均方根误差评判的方式对3种不同方式的标定精度进行评价。假设真实的角点的三维世界坐标的值为(X,Y,Z),通过不同标定方式计算获得的三维世界坐标值为(Xi,Yi,Zi)。其中i可取C、O、M分别代表3种不同的标定方式下计算出的三维世界坐标的实际的值。故此标定精度的均方差计算公式设定为：

(10)

通过式(10)的计算，最终针对6组测试集采用3种不同标定方法计算出的均方根的误差如表6所示。

从表6中数据可以看出采用本文提出的方法的双目相机的标定误差的平均均方根约为0.038 mm。采用基于Opencv和Matlab标定的方法获得的双目相机标定的平均均方根误差分别为0.155 mm和0.417 mm。相比而言，其标定精度分别提高了75%和90%。从图7中也能清晰看出3种不同方法的标定误差的均方根的变化，采用本文提出的方法的标定的精度和稳定性相对较好。

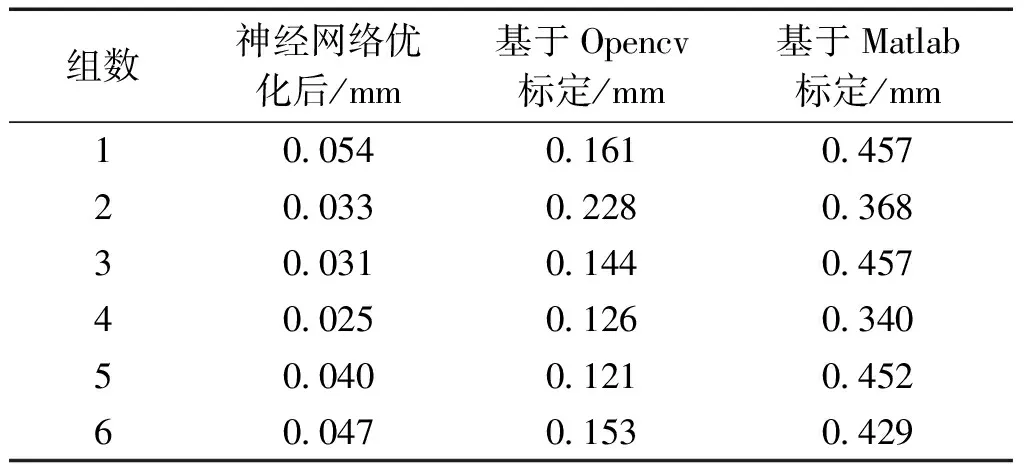
表6 不同方法标定的误差的均方根

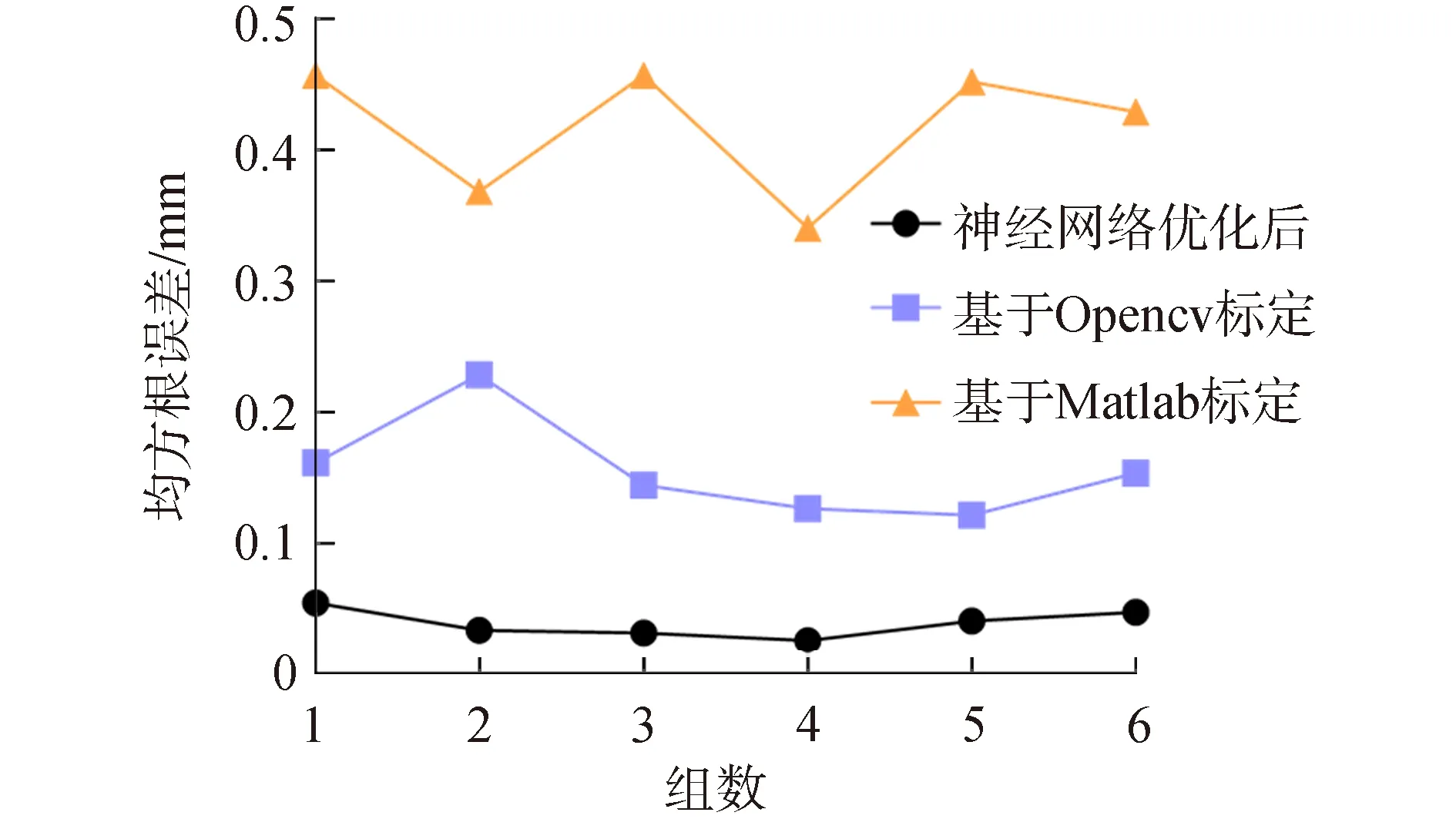
图7 基于不同方法的标定误差均方根变化

进一步从每个三维坐标的X、Y、Z轴的误差分别进行分析，如图所示。从图8中可以看出采用本文提出的方法在X、Y、Z3个方向的误差均比较小，而且整体的稳定性相对较高。通过3种不同的方法最终计算出的三维世界坐标的各个方向的误差分布图，更加清晰证明本文提出的方法的有效性和稳定性。

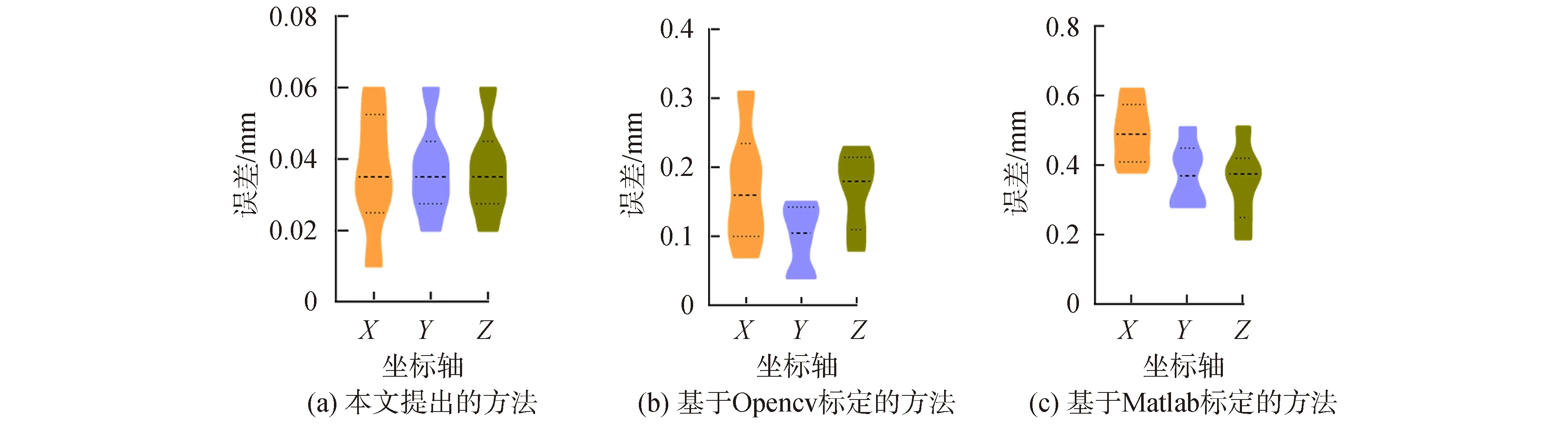
图8 基于不同方法的角点的三坐标标定误差分析

3.3.3 不同方法的标定速度对比实验

针对上述3种不同方法进行双目相机标定时的速度进行测试。按照相同的环境同样的硬件条件下进行5组实验测试，最终标定花费的计算时间如表7所示。

从表7中的数据可以看出采用本文方法进行双目相机标定时需要的平均时间为26.3 s,采用Opencv和Matlab标定时所需要的平均时间分别为5.8 s和6.6 s。相比而言采用本文提出的方法所需要花费的时间较长，主要因为需要进行大量的训练集进行训练。在训练的过程中不断调整神经网络的权重值，使其标定的精度不断提高。

4 结论

1)本文提出的基于差分遗传算法优化BP神经网络来进行双目相机标定的方法最终获得的标定误差的均方根为0.038 mm。

2)与传统的基于Opencv和Matlab的方法相比，不仅简化了标定的流程，降低了计算的复杂度，同时还提高了标定的精度。从实际的实验结果进行分析，完全符合双目相机标定的精度需求。

在实际的应用过程中，由于神经网络训练需要大量的数据集，因此在数据集的采集和训练所花费的时间相对较多。然而一旦神经网络达到训练设定的要求，后续的标定速度将会非常快。于此同时基于本文提出的方法标定的精度受数据集量的大小的影响，由于实验条件的限制选取了一部分实验数据，因此其实际的标定精度可以进一步的提高。