降低超声速飞行器声爆的一种主动控制方法

叶柳青, 叶正寅, 马博平

(西北工业大学 航空学院, 陕西 西安 710072)

声爆是飞行器在超声速飞行时特有的一种声学现象[1-5]。飞行器超声速飞行时在其近场会产生以激波为主的一系列扰动波，它们在大气层中自然非线性传播，最终在远场演化为“N”形声波。这种“N”形声波表示压力信号的形状，是由头部激波和尾部激波组成。激波的厚度很小，经过激波后空气的压强、密度、温度都急剧升高，速度急剧下降。被这两道激波扫过的任何空间中的物体都会感觉到强烈的变化，人的耳膜受到突然的空气压强变化，感觉是两声巨响，这两声巨响即为声爆[6-9]。

Seebass等首次提出了基于线化理论SGD(Seebass-George-Darden)方法来降低声爆，为低声爆超声速客机设计奠定了理论基础[10-11]。冯晓强等[12]基于SGD方法，首次提出一种“梭式”布局静音超声速客机方案。朱自强等[13]对目前降低声爆的优化设计方法进行了详细的介绍与讨论。徐悦等[14]通过求Euler/N-S方程计算了2个典型低声爆构型国际标准算例(即SEEB-ALR旋成体和三角翼)的近场声爆信号，他们指出在计算上述标准算例的简单绕流场近场声爆时，流场的黏性效应不是必须考虑的因素。Howe[15]提出了一个“静音锥”概念来降低声爆水平。主要是在机头上安装一个可伸缩的静音锥，产生一系列弱激波，从而达到降低声爆的目的。国内李占科等[16]和冯晓强等[17]研究了不同参数的单级和多级静音锥对超声速声爆水平的影响。在“静音锥”概念的启发下，沈沉等[18]和翟荣华等[19]提出在超声速客机机头安装合适的细长杆来降低声爆的方案，并基于AUSM+格式和Fluent的准三维数值模拟手段对多组细长杆设计方案进行了模拟分析，计算结果表明6 m长的12.5°半锥角单级锥形细长杆具有明显的降噪效果。然而，附加的静音锥或细长杆会显著增加飞机的质量，必须配备足够的刚度以避免气动弹性不稳定。

吸喷气是常用于飞行器流动控制的一种较为成熟的技术手段[20-22],如合成射流技术[20]、边界层吹吸气以及协同射流控制技术等[21-22]都采用吸喷气对流动进行控制。本文创新地将吸喷气应用于超声速声爆抑制中，主要是在翼型下表面前缘附近处开口进行吸气，同时在翼型下表面后缘附近处开口进行喷气，且保持吸气量与喷气量相等。这种方法不仅避免了质量损失、大幅度增加阻力，以及牺牲机身空间等不利影响，还具有操作简单、易于控制等优点。为了节约能源，当超声速飞机在人口密度较大的城市上空飞行时，吸气口和喷气口是打开的，而当飞机飞越海面或者沙漠时，吸气口和喷气口关闭。为了验证所提出的低声爆方法的有效性，将该主动控制方法应用于菱形翼型NACA0008翼型中，首先采用CFD方法求解Euler方程得到近场过压分布，再使用自研的远场传播工具将近场过压分布传播至地面，将最终得到的地面声爆波形与使用该主动控制方法之前的基准菱形翼型的NACA0008翼型进行对比。并进一步研究了吸气口与喷气口的位置、气体质量流量以及飞行迎角对地面声爆最大过压、阻力系数、升力系数以及升阻比的影响。

1 降低声爆的主动控制方法

本文创新地提出了一种可有效降低超声速飞行器声爆水平的方法，该方法主要是在翼型下表面前缘附近处开口进行吸气，同时在翼型下表面后缘附近处开口进行喷气，且保持吸气量与喷气量相等。该方法的气动原理是：飞行器超声速飞行时，翼型下表面前半部分的流场是由激波主导的，通过在翼型下表面前缘附近处开口进行吸气，产生一系列膨胀波，通过膨胀波与前缘激波相互作用，达到削减头部激波峰值的效果；翼型下表面后半部分的流场是由膨胀波区主导的，通过在翼型下表面后缘附近处喷气，产生激波来减弱后缘激波峰值。由于前后缘激波峰值的减小，传播到远场处的噪声值也会相应的降低。

为了说明本文提出的降低声爆的主动控制方法的有效性，这里选择菱形翼型和NACA0008翼型作为基准翼型。图1a)至1b)分别展示了基准翼型以及使用该主动控制方法后的翼型。c代表弦长。气流通过吸气口时，保持气流方向与吸气口所在表面垂直。同样地，气流通过喷气口时，保持气流方向与喷气口所在表面垂直。为了最大限度地降低功耗，从翼型前缘附近处吸入的气流流量与从后缘附近处喷出的气流流量相等。流动控制由泵进行驱动。

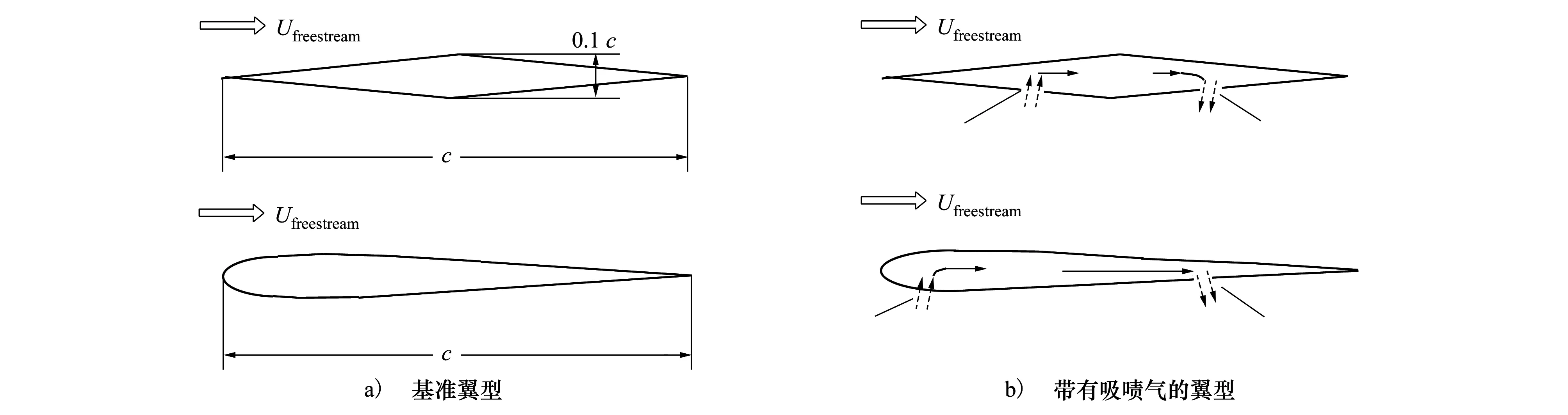
图1 基准翼型与带吸喷气的翼型

2 数值方法

精确地评估超声速飞行器飞行时地面感受到的声爆噪声水平是使用低声爆方法来降低声爆的先决条件[1-2]。目前国际上主流的声爆预测策略主要分为2个步骤[2]：①首先通过风洞试验或者CFD方法得到近场过压分布；②运用修正线化理论或非线性声学理论将近场的过压分布传播到远场，最终获得地面声爆的声压信号。噪声级有多种衡量标准，不同衡量标准间的差异较大。在获得地面声爆波形后，作为远场N波的主要参数，许多国内外的研究者，如翟荣华等[19]和Sun等[23]均采用地面声爆波形中的最大过压值来量化声爆水平。因此，这里也将声爆最大过压作为声爆强度的主要指标。

2.1 近场CFD计算数值方法

采用商业CFD软件，即Fluent,对二维欧拉方程进行求解，从而得到近场的压力分布。利用ICEM软件来生成结构网格。为了更加精确地捕捉激波特性，令网格面平行于激波面，并且对激波附近的网格进行加密。本文求解Euler方程来实现近场声爆的预测，其二维守恒形式的Euler方程为

(1)

式中，U为守恒变量,对流通量F(U)=(f(U),g(U)),表达式分别为

式中：ρ为密度;υ1和υ2为x,y方向的速度分量;E为单位总能;p为压强;h为单位总焓。

在进行数值计算中,选取Density基函数,求解法选择隐式,无黏通量项采用Roe格式。

2.2 声爆远场分析数值方法

在远场分析中,本文采用自研的基于Whitham修正线化理论、Thomas波形参数法和几何声学的综合声爆信号传播与分析工具(FL-BOOM)将近场声爆信号传播到远场。线化声爆预测理论是Whitham于1952年由线化超声速细长旋成体理论发展而来。Whitham认为,线化超声速细长旋成体理论中关于特征线是相互平行的假设在声爆计算中不合理,于是对特征线方程进行非线性修正,提出了声爆的线性理论,并给出了精度较高的特征线描述。

由线化超声速细长旋成体理论可以得到旋成体的小扰动速度表达式,如(2)式所示

(2)

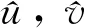
修改特征线方程x-Br=const为x-Br=y(x,r),即x与r的关系不是简单的线性关系,而是与空间点坐标(x,r)有关,于是(2)式可写为

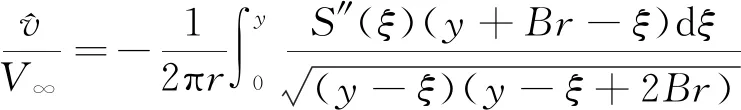
(3)

对于特征线方程的确定,这里给出特征线的表达式

(4)

F(y)为根据线化理论水平方向速度分量积分式近似出的Whitham“F-函数”。根据线化Bernouli方程可获得激波,其强度为

Δp/p0=γMa(2βr)-1/2F(y)

(5)

式中:γ为比热比,Δp/p0为声爆过压,Δp=p-p0,p为观测点当地压强,p0为环境压强。

3 结果与讨论

在数值计算中选取飞行马赫数为1.7。翼型弦长c=1 m。 吸气口处的边界条件设置为压力出口边界条件,喷气口处的边界条件设置为速度入口边界。通过调整速度入口边界处的速度大小,来保持吸气口处的气流流量与喷气口处的气流流量一致。在翼型下方两倍于翼型弦长的位置(即H/L=2,其中L=c)采集近场过压信号。假定飞行器巡航高度为16 764 m,飞行迎角为0°,用自研的FL-BOOM工具将近场过压信号传播到远场得到地面声爆波形。

3.1 近远场预测工具的正确性与一致性验证

表1给出了由不同方法计算的菱形翼型气动力系数。由表中数据可知,由商业软件Fluent计算得到的菱形翼型阻力系数为0.029 18,理论方法计算得到其的阻力系数为0.029 10,二者相比,误差仅为0.27%,表明所使用的数值方法具有较高的精度,可以用来后续研究。

表1 不同方法计算的菱形翼型气动力系数及其误差

为验证波形参数法的计算结果,本文使用声爆标模LM1021进行验证。远场传播条件如表2所示。图2为FL-BOOM计算的LM1021远场压力信号,作为对比的是SBPW-1参会代表提交的结果(图中以S开头的数据)对比。总体来看,本文计算的远场声爆波形与参会代表提交的结果吻合较好,表明FL-BOOM可用于后续的声爆远场波形预测。

表2 远场传播条件

图2 无黏条件下FL-BOOM计算验证

3.2 网格无关性验证

基于ICEM软件,分别生成3套不同网格数量的结构网格,并将不同网格密度下带有吸喷气口的翼型的近场压力分布进行比较,以验证网格无关性,如图3所示。对于带吸喷气的菱形翼型,3套网格的节点数分别为190×200,290×400和390×800分别对应于疏网格、中等网格和密网格。吸/喷气口分别位于距离前缘21.0%/79.0%弦长位置处。吸气口与喷气口的长度都为2%的弦长,并且质量流率都为1 kg/s。对于带吸喷气NACA0008翼型,3套网格节点数分别为190×206,380×412,760×823。吸/喷气口分别位于距离前缘16.1%和79.3%弦长位置处。吸气口与喷气口的长度都为2%的弦长,并且质量流率都为1.9 kg/s。

从图3及其局部放大图可以看出,不同网格密度下,激波与膨胀波的位置基本保持一致。但是采用较密的网格得到的激波与膨胀波的峰值会更大,这是由于较密的网格数值耗散较小。对于带吸喷气的菱形翼型和NACA0008翼型来说,当网格节点数分别达到290×400和380×412时,网格数量对计算结果的影响可以忽略。

图3 网格密度对近场压力分布的影响

3.3 吸气口与喷气口位置的影响

图4和图5分别表示以菱形翼型和NACA0008翼型作为基准翼型时,吸气口或者喷气口位置对地面声爆最大过压的影响。Δp-o(maximum overpressure)代表前缘激波处的最大过压,为正值。Δp-u(maximum underpressure)表示后缘激波处的最大过压,为负值。x代表开口(吸气口或者喷气口)中心距翼型前缘的距离。这里研究吸气口位置的影响时,关闭喷气口。同样的,研究喷气口位置的影响时,关闭吸气口。

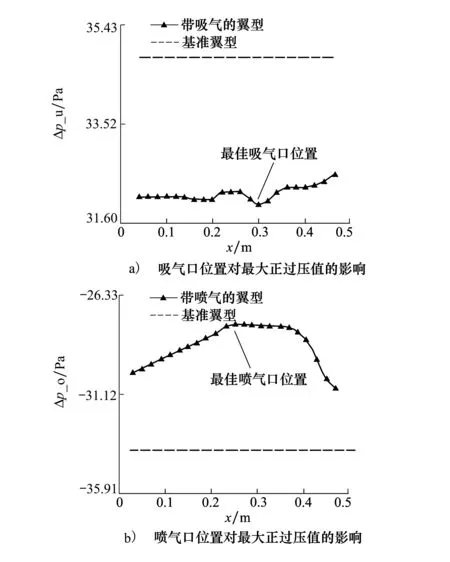
图4 基准菱形翼型和带吸喷气菱形翼型最大过压的对比

图5 基准NACA0008翼型和带吸喷气NACA0008翼型最大过压的对比

对于基准翼型为菱形翼型来说,吸气口长度为4%的弦长,吸气口中心位置从距翼型前缘0.04 m到0.46 m变化,中间间隔为0.02 m,吸气口处质量流率为-6.428 kg/s。从图4a)可以看出打开吸气口后,翼型前缘激波处的最大正过压值低于基准翼型,这表明在翼型前缘附近处吸气可降低声爆水平,并且当吸气口位于距前缘0.3 m时,前缘激波处的最大正过压值最小。因此,吸气口位于距前缘0.3 m位置处为最佳吸气口位置。关闭前缘附近吸气口,只打开后缘附近喷气口,喷气口的长度为2%的弦长,喷气口中心位置从距翼型前缘0.53 m到0.97 m变化,中间间隔为0.02 m,喷气口处的质量流率为2.5 kg/s。从图4b)可以看出打开喷气口后的菱形翼型后缘激波处的最大负过压值高于基准翼型,但其绝对值明显低于基准翼型,这表明在翼型后缘附近处喷气可降低声爆水平,并且当喷气口位于距前缘0.75 m时,翼型后缘激波处的最大负过压值绝对值最小,因此,喷气口位于距前缘0.75 m位置处为最佳喷气口位置。

对于基准翼型为NACA0008翼型来说,只打开前缘吸气口,吸气口长度为2.4%的弦长,吸气口中心位置从距翼型前缘0.022 5 m到0.334 5 m变化,中间间隔为0.048 0 m,吸气口处的质量流率为-6.887 7 kg/s。图5a)展示了吸气口位置对最大正过压值的影响。关闭前缘吸气口,只打开后缘喷气口,喷气口长度为2.4%的弦长,喷气口中心位置从距翼型前缘0.619 5 m到0.955 5 m变化,中间间隔为0.024 0 m,喷气口处质量流率为3.356 97 kg/s。图5b)展示了喷气口位置对最大负过压值的影响。类似于上面对基准翼型为菱形翼型的分析,从图5中可以确定最佳吸气口的位置为吸气口中心距离前缘0.046 55 m位置处,最佳的喷气口位置为距前缘0.693 0 m位置处。

总的来说,图4和图5的结果显示不论在翼型的前缘附近处吸气还是在后缘附近处喷气,都可有效地降低声爆水平。另外一方面,也可以看出本文提出的主动控制方法不仅适用于基准菱形翼型,也同样适用于基准NACA0008翼型。

3.4 气体质量流量的影响

吸气口与喷气口处气体的质量流量是一个重要的参数,会对最终降噪的效果产生影响。分别将吸气口与喷气口设置于3.3小节中确定的最佳位置处,同时打开吸气口与喷气口,并保持吸气口处气流的质量流量与喷气口处气流的质量流量相等。根据文献[21-22],为避免等质量吸气时在吸气口发生壅塞,吸气口长度应该大于喷气口的长度。这里,对于带吸喷气的菱形翼型,吸/喷气口长度分别取4%和2%的弦长。图6和图7展示了吸气口与喷气口处的气流质量流量对地面声爆波形、最大过压、阻力系数以及升阻比的影响。对于带吸喷气的NACA0008翼型,吸/喷气口长度分别取4.8%和2.4%的弦长。图8和图9展示了气流质量流量对地面声爆波形、最大过压、阻力系数以及升阻比的影响。

图6 不同质量流量下基准菱形翼型与带吸喷气的菱形翼型的计算结果对比

图7 在质量流量为6.5 kg/s时基准菱形翼型与带吸喷气的菱形翼型的地面声爆波形对比

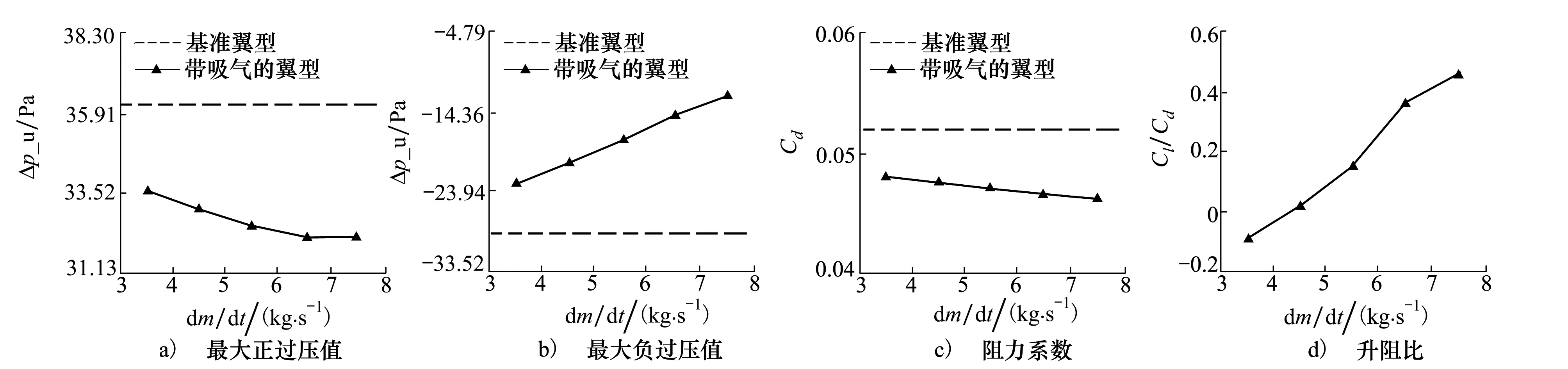
图8 不同质量流量下基准NACA0008翼型与带吸喷气的NACA0008翼型的计算结果对比

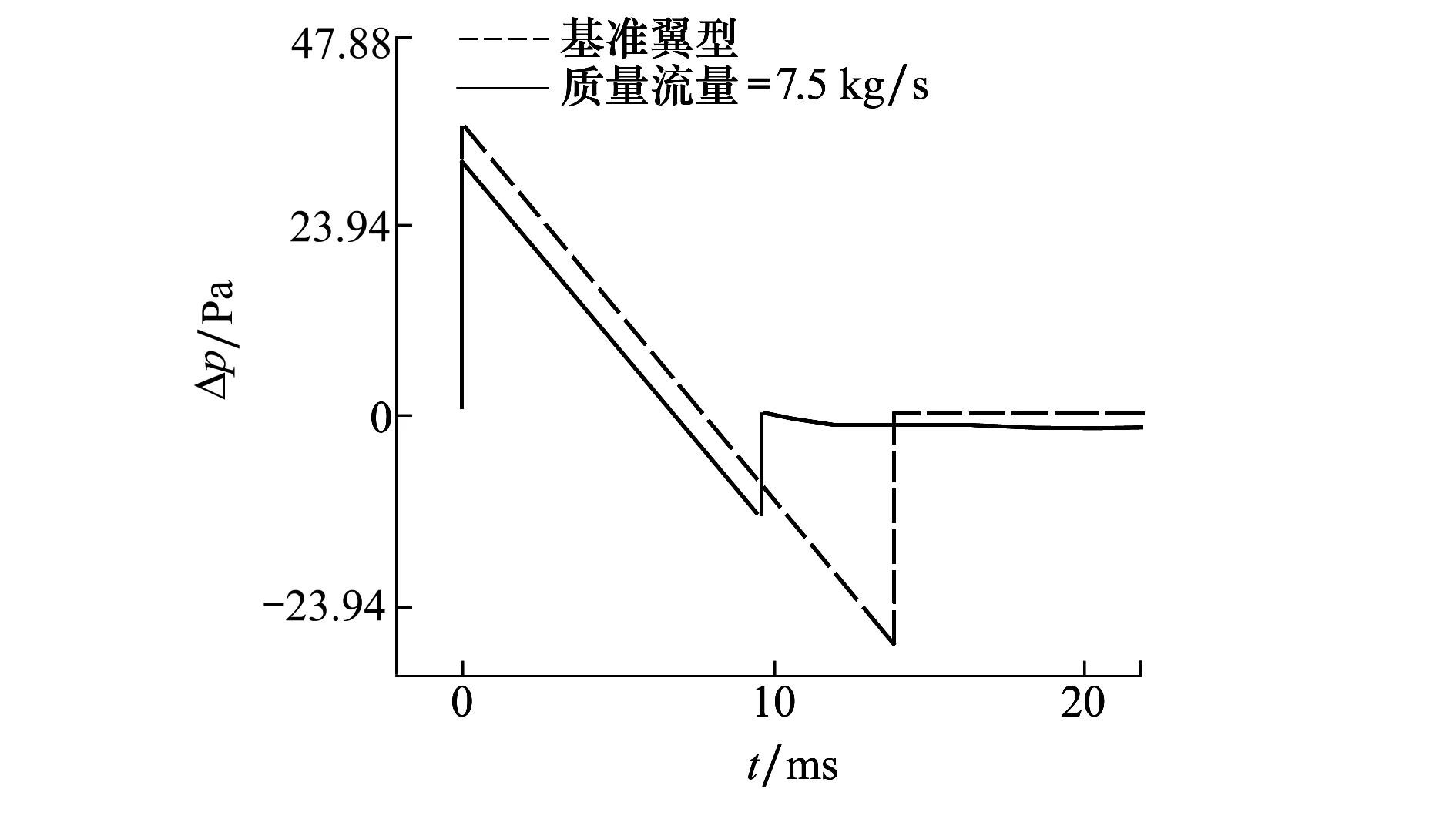
图9 在质量流量为7.5 kg/s时基准NACA0008翼型与带吸喷气的NACA0008翼型的地面声爆波形对比

从图6a)～6b)中可以看出,与基准菱形翼型相比,带吸喷气的菱形翼型的前缘激波处的最大正过压值变小,后缘激波处的最大负过压值变大,但其绝对值变小,这表明在菱形翼型前缘附近处吸气并同时在翼型后缘附近喷气的方法可以有效降低声爆水平。从图中还可以看出,随着吸喷气口处气体的质量流量的增大,前缘激波处的最大正过压值不断减小,后缘激波处的最大负过压值不断增大,但其绝对值仍不断减小,这表明增大吸喷气口处气体的质量流量可以增强降噪效果。从图6c)中可以看出,与基准菱形翼型相比,带吸喷气的菱形翼型的阻力系数变小,并且随着气流质量流量的增大,阻力系数不断减小。在气体质量流量为6.5 kg/s时,前缘激波处的最大正过压值降低了12.87%,后缘激波处最大负过压值的绝对值降低了33.83%,阻力系数降低了9.50%。从图6d)可以看出,随着气流质量流量的增大,升阻比也不断增大。这说明本文提出的主动控制方法不但能够有效降低声爆水平,而且还会带来气动特性的显著提升。对于主动流动控制而言,若评判其气动效率如升阻比L/D,应该将喷吸气的功耗也考虑进来,参考文献[21-22]中功耗的计算方法,图6e)给出了不同气流质量流量下菱形翼型吸喷气消耗的功率系数。从图中可以看出,气流质量流量越大吸喷气消耗的功率系数也越大。因此,结合上面的分析可知,若想达到降低音爆的最佳效果,应该在功耗允许范围内尽可能地提高吸喷气口处的气流质量流量。

从图8和图9中可以看出,吸喷气口处气体的质量流量对基准翼型为NACA0008翼型的地面声爆波形、最大过压、阻力系数以及升阻比的影响规律与菱形-SI翼型基本一致,这里就不展开描述。对带吸喷气的NACA0008翼型来说,当气体质量流为7.5 kg/s时,前缘激波处的最大正过压值降低了12.85%,后缘激波处的最大负过压值的绝对值降低了56.77%,阻力系数降低了10.96%。

总的来说,增加吸喷气口处气体的质量流量会导致声爆水平与阻力的进一步降低,并且后缘附近处喷气比前缘附近处吸气更容易达到降噪的效果。

因此,在使用本文提出的降低声爆的主动控制方法时,若想要达到较好的降噪效果,可尽量提高吸气口与喷气口处气体的质量流量。

3.5 飞行迎角的影响

图10和图11展示了在不同迎角时,将本文提出的主动控制方法应用于菱形翼型与NACA0008翼型时的降噪效果和气动性能。同时打开翼型前缘附近处的吸气口与翼型后缘附近处的喷气口,将吸/喷气口分别放置在其对应的最佳位置处,并保持吸气口处气流的质量流量与喷气口处气流的质量流量相等。其中,对于带吸喷气的菱形翼型来说,吸/喷气口长度分别为2%和为4%的弦长;对于带吸喷型还是带吸喷气NACA0008翼型,吸/喷气口长度分别为2.4%和为4.8%的弦长。无论对于菱形翼型还是NACA0008翼型气体的质量流量都为3.5 kg/s。

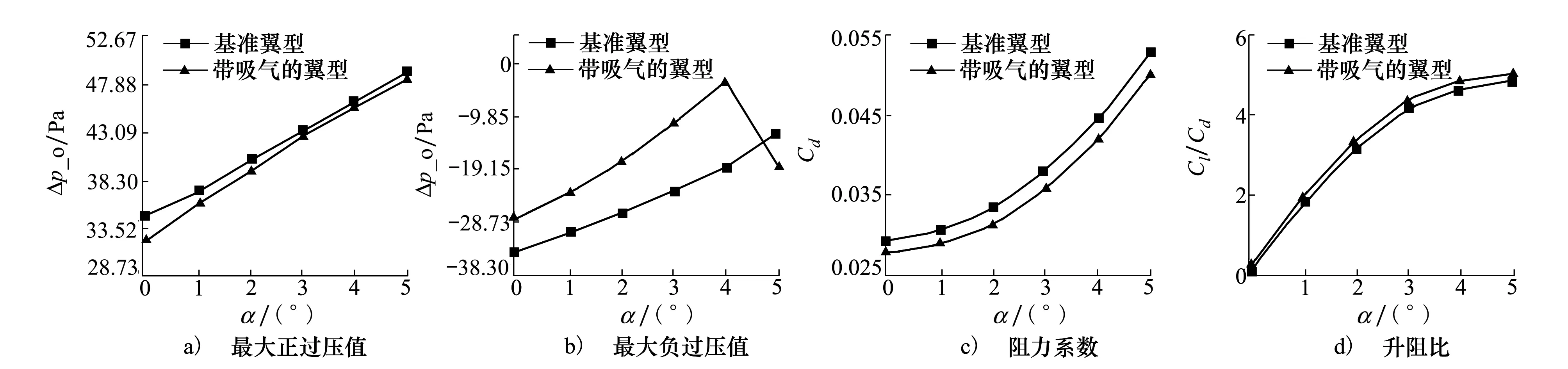
图10 不同迎角下带吸喷气的菱形翼型与基准菱形翼型的计算结果对比

图11 不同迎角下带吸喷气的NACA0008翼型与基准NACA0008翼型的计算结果对比

图10和图11的结果显示,在不同的飞行迎角下,与相对应的基准翼型相比,带吸喷气的菱形翼型与带吸喷气的NACA0008翼型的前缘激波处的最大正过压值略微降低,而后缘激波处的最大负过压绝对值显著降低,阻力系数明显降低,升阻比基本不变。然而,从图10b)和图11b)还可以看出,当迎角增大到5°时,带吸喷气的菱形翼型后缘激波处的最大负过压绝对值超过了基准菱形翼型;当迎角为3°时带吸喷气的NACA0008翼型后缘激波处最大负过压绝对值也超过了基准NACA0008翼型。这说明本文提出的降低声爆的主动控制方法适用于小迎角范围。

为了验证本文进行近场声压信号采集的位置(即H/L=2)是合适的,这里选取不同的位置进行近场声压信号采集,再将其传播到远场得到地面声爆信号,如图12所示。将吸/喷气口分别放置在其对应的最佳位置处。对于带吸喷气的菱形翼型,吸/喷气口长度分别为0.02c和0.04c,吸喷气口处气体的质量流量为6.5 kg/s。对于带吸喷气的NACA0008翼型,吸/喷气口长度分别为0.024c和0.048c,吸气喷气口处气体的质量流量为7.5 kg/s。从图12可以看出,由位置H/L=2处得到的地面声爆波形中的最大过压与H/L=5以及H/L=7得到的结果是基本一致的。这说明本文进行近场声压信号采集的位置(即H/L=2)是合适的。

图12 不同位置处采集近场压力信号得到的地面声爆波形对比

4 结 论

本文创新地提出了一种可降低超声速飞行器声爆的主动控制方法,具体为翼型下表面前缘附近处开口进行吸气,同时在翼型下表面后缘附近处开口进行喷气,且保持吸气量与喷气量相等。为了验证所提出低声爆方法的有效性,将该主动控制方法应用于菱形翼型和NACA0008翼型中,并进一步研究了吸气口与喷气口的位置、气体质量流量以及飞行迎角对地面声爆波形、最大过压、阻力系数以及升阻比的影响,得到的结果主要如下:

1) 该方法能够显著地降低超声速飞行器的声爆水平以及阻力,并且后缘处喷气比前缘处吸气更容易达到降噪的效果;从气动角度看,该方法在降低声爆的同时能够兼顾气动性能;

2) 增加吸气口与喷气口处气体的质量流量将会进一步增强降噪效果。将该主动控制方法应用于菱形翼型后,在气流质量流量为6.5 kg/s时,最大正过压值降低了12.87%,最大负过压值的绝对值降低了33.83%,阻力系数降低了9.50%;将该主动控制方法应用于NACA0008翼型后,在气体质量流量为7.5 kg/s时,最大正过压值降低了12.85%,最大负过压值的绝对值降低了56.77%,阻力系数降低了10.96%;

3) 该降低声爆的主动控制方法适用于小迎角范围。

为了节省能源,吸气口与喷气口可在人群密度较大的城市上空打开使用,而在海面或者沙漠上时关闭。可见本文提出的低声爆方法效果良好,控制灵活,为新一代低声爆超声速客机的设计提供了有益的参考。