基于OpenFOAM的正十二烷喷雾燃烧数值模拟

2021-07-12李文刚肖隐利路易聘曹志博吴娟

西北工业大学学报 2021年3期

李文刚, 肖隐利, 路易聘, 曹志博, 吴娟

(西北工业大学动力与能源学院, 陕西西安 710072)

随着世界范围内能源危机与环境污染的加重，高效能低排放已成为航空发动机设计需要考虑的重要因素。开发先进的燃烧控制方法是实现低排放的重要手段，为此，需要全面掌握燃烧特性，如点火延迟时间、火焰浮升高度和火焰稳定机理等。为了实现这一目标，ECN[1]为国际试验和数值模拟的合作提供了一个开放可存取的数据库和论坛。

ECN将正十二烷的喷雾燃烧称为Spray A，由于常用柴油的化学成分复杂，其热力学性质和化学性质很难获得。因此，ECN刚开始数值模拟时采用易于操作且化学反应动力学已被广泛验证的正庚烷替代柴油。然而典型柴油碳链是由10～25个碳原子组成，因此正庚烷并不能较好地反映柴油的热物理性质，尤其是柴油的沸腾和蒸发等性质，而这些性质对准确预测柴油喷雾燃烧的点火延迟时间和火焰浮升高度等参数至关重要。而正十二烷有更长的碳链，热物理性质和输运性质明确，更适合替代柴油燃料。近年来，许多学者和研究人员意识到开发正十二烷合适的化学反应机理的重要性，Luo等[2]开发并验证了一个包含106组分420基元反应的正十二烷骨架机理，采用非定常雷诺时均法(URANS)验证了射流喷雾燃烧；斯坦福大学的Narayanaswamy等[3]开发了一个包含257组分1 521基元反应的正十二烷反应机理；Ranzi等[4]开发了一个130组分2 395基元反应的正十二烷反应机理。清华大学的Yao等[5]开发并验证了一个54组分269基元反应的正十二烷骨架机制。

Spray A有大量可用的试验数据，包括环境温度、环境密度、燃油注入压力等参数变化相对应的试验数据，ECN团队利用高速摄像技术得到了正十二烷喷雾的瞬态过程，利用Mie散射和Rayleigh散射技术对无反应情况下气体的混合情况进行定量测量[6]。

针对Spray A，不同的研究人员采用不同的湍流模型和燃烧模型进行了广泛的数值研究。早些年，由于计算机资源的限制，大部分的数值研究是基于非定常雷诺时均法(URANS)下的求解器进行的，Errico等[7]采用与参考文献[2]相同的正十二烷化学机理，比较了良好混合(well-mixed)燃烧模型和多代表交互小火焰(multiple Representative Interactive Flamelet，mRIF)燃烧模型分别在Spray A不同环境温度和氧气浓度条件下的情况，结果表明，采用well-mixed模型能够准确地预测点火延迟，但高估了热释放率，预测的燃烧室压力偏高，进而影响对污染物排放的准确预测，相比之下mRIF燃烧模型结果更好，与试验结果有较高的一致性；Bhattacharjee和Haworth[8]研究了不同环境参数对Spray A的影响，此研究使用二维RANS结合输运概率密度函数(TPDF)的方法来模拟反应扩散过程。

大涡模拟(LES)近些年被广泛地应用于Spray A的数值研究中，Salehi等[9]首次将LES与多映射调节(multiple mapping conditioning,MMC)模型相结合应用于Spary A，发现Spray A火焰稳定发生在具有显著湍流化学相互作用的区域，在靠近喷嘴出口液相会影响火焰；Wehrfritz等[10]基于OpenFOAM平台，采用LES和火焰面生成流(flamelet generated manifold,FGM)方法对不同的环境氧气浓度条件下的Spray A进行模拟，使用拉格朗日粒子追踪(Lagrangian particle tracking)方法描述液滴颗粒，比较了参考文献[3]和参考文献[4]中2种正十二烷详细机理的表现，发现2种化学机制在点火特性存在显著差异，但对于稳定火焰来说，差别不大，该研究首次量化了燃油喷嘴出口与火焰浮升高度之间的冷焰结构(cool flame)，还发现在较低环境气量浓度下，火焰浮升高度预测很好，21%的氧气浓度下，对火焰浮升高度预测过高；Cheng等[11]采用LES方法对900 K和1 000 K 2个环境温度的Spray A进行数值模拟，预测了Spray A两级点火行为，结果表明，第一级着火发生在贫燃混气中，第二级着火在富油混合气中发生，贫燃混气中的第一级点火促进了富燃料混合气中的第一级和第二级点火，用自燃和火焰传播与低温点火耦合2种机理来解释燃烧过程的火焰浮升高度和稳定性，2种机理相互竞争，关键取决于环境温度。

虽然Chomiak和Karlsson[12]采用了部分搅拌反应器(PaSR)模型研究正庚烷的喷雾射流燃烧，但还未发现基于PaSR燃烧模型的正十二烷喷雾射流燃烧数值模拟报道，基于此，本文采用PaSR燃烧模型与一个包含54组分269基元反应的正十二烷骨架机制相结合，对Spray A进行数值研究。

1 物理模型和数值模拟方法

1.1 物理模型与网格划分

Spray A喷雾燃烧器和截面结构示意图如图1所示，该燃烧器是由Sandia国家实验室(SNL)构造的一个特征长度为108 mm的定容立方体，燃油喷嘴安装在立方体上表面正中心处。数值模拟工况严格按照试验条件设置，试验具体条件如表1所示，有反应和无反应2种情况燃烧室气体组分如表2所示。

图1 SNL喷雾燃烧器及截面结构示意图

表1 Spray A试验条件H

表2 燃烧室气体组分(体积分数) %

对计算网格的划分,为了提高数值模拟计算效率,定容燃烧室简化为一个长方体,其底面为边长70 mm的正方形,长方体高108 mm。非均匀结构网格使用OpenFOAM网格生成字典blockMeshDict生成,利用网格加密字典refineMeshDict进行一次加密,加密区域为一个底面与燃油注入平面重合的长方体,底面为边长16 mm的正方形,正方形中心与燃油喷嘴重合,高为78 mm,其二维截面如图3所示。以便更好预测喷雾射流性能参数,总体六面网格数量约27.7万,加密后最小网格尺寸为0.25 mm,纵横比约2.3。

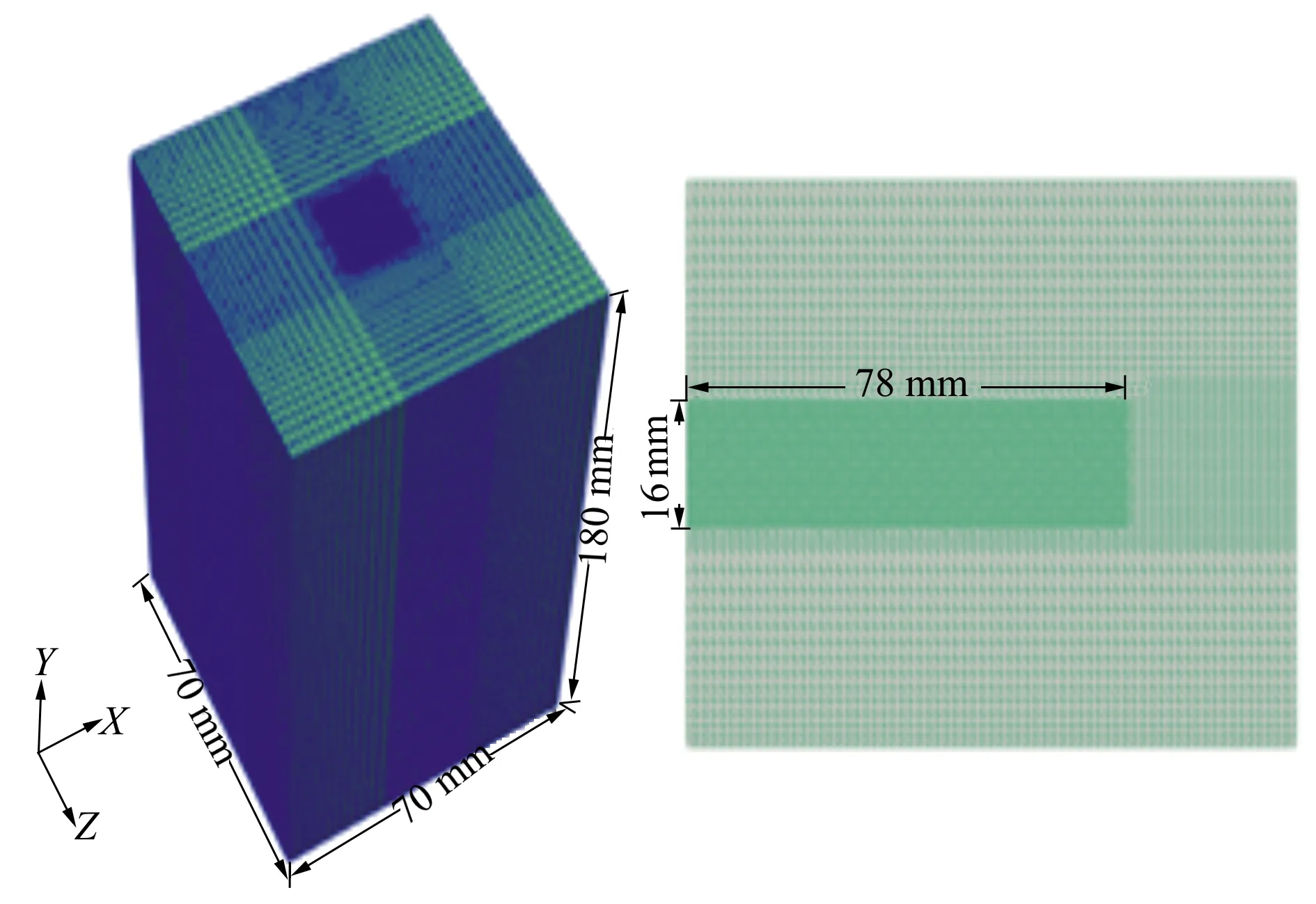
图2 三维结构网格图3 三维网格加密区域

1.2 PaSR燃烧模型

PaSR模型通过求解组分输运方程的方法来封闭湍流模型中的反应源项。该模型假设火焰结构比计算网格单元小得多,一个网格单元可分为反应区和非反应区,在非反应区,只发生反应物之间的混合,在反应区是一个完全搅拌反应区,在反应区中,化学时间尺度要远远大于湍流时间尺度。

假设整个计算网格单元是完全搅拌反应PSR,某反应物的初始平均浓度为c0,k,在时间t内反应物平均浓度从c0,k变化为ck,那么在时间t内,PSR网格单元中的平均反应速率如下表示

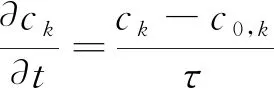
(1)

PaSR计算网格反应物平均浓度想要达到ck,需要额外的时间τ,那么平均反应浓度ck可以表示为

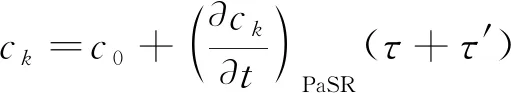
(2)

则PaSR计算网格反应物平均反应浓度c1,可表示为

c1=k*c+(1-k*)c0

(3)

式中：

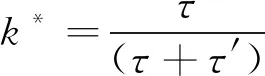
(4)

k*为在一个PaSR计算网格中PSR反应区所占的体积分数,由于τ′与反应区与和非反应区的组分之间的混合过程相关,所以将τ′通常被称为混合时间尺度τmix。在k-ε中可以通过公式(5)得到混合时间尺度

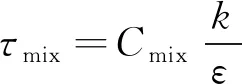
(5)

式中，Cmix是经验确定的模型常数,其值为0.03。

1.3 Reitz-KHRT雾化模型

Reitz-KHRT模型是一种二次雾化模型,该模型认为经过初次雾化的较大液滴在喷雾场中同时受到2种不稳定波的作用,一种是K-H(Kelvin-Helmholtz)不稳定波,另外一种为R-T(Rayleigh-Taylor)不稳定波。K-H模型认为液滴受到空气动力作用,引起K-H不稳定波增长导致气液界面不稳定性,最终导致液滴分裂破碎;R-T模型认为是由于受到R-T波的不稳定性增长导致液滴分裂破碎(R-T波是指在气液界面上沿着流动方向的波)。在子液滴雾化时,K-H模型和R-T模型是竞争关系,对一个将要破碎的液滴,判断其增长最快的扰动波长度与液滴直径的大小关系,若增长最快的扰动波长度小于液滴直径,液滴发生RT破碎;否则判断液滴韦伯数We是否大于临界韦伯数Wecr(通常取Wecr值12.5),若是,则发生K-H破碎。

1.4 数值模拟方法

本研究的求解器基于开源CFD框架OpenFOAM下的标准求解器SprayFoam。SprayFoam是一个瞬态求解器,适用于可压缩的湍流气液两相喷雾燃烧;喷雾采用欧拉-拉格朗日方法进行模拟,气相在欧拉框架下使用非定常雷诺时均法(URANS)进行描述,液相在拉格朗日框架下使用拉格朗日粒子追踪的方法(LPT)进行处理;湍流模型采用Realizek-ε模型,燃烧模型采用PaSR模型,化学机理采用一个包含54组分269基元反应的正十二烷的骨架机制[5]。计算过程中动态调整时间步长,约5×10-7s,最大库朗数不超过0.25,确保计算的稳定性,模拟结束时间设置为1.5 ms,此时,无反应情况下液体穿透长度稳定在10 mm左右,有反应情况下火焰形成准稳态火焰结构,对模拟结果不会产生影响。

液相雾化子模型中燃油注入采用Blob模型,液滴受到作用力为球形阻力模型,初次雾化采用LISA模型,二次雾化采用Reitz-KHRT模型,蒸发模型为liquidEvaporation模型;燃油注入持续1.5 ms,总共注入18 000 000个液体颗粒包(liquid parcels),液体颗粒包由一群具有相同直径和动量的液体颗粒组成;液滴的分布采用Rosin-Rammler模型,其中,设置液滴直径最大值与喷嘴内径相同,分布指数n设置为3;喷雾半角设置为10°。

压力速度方程由PIMPLE算法耦合,PIMPLE算法结合了SIMPLE和PISO算法,适用于非定常求解器,确保了稳定性和准确性。扩散项采用二阶中心差分格式,对流项采用二阶TVD中心差分格式,时间项采用一阶隐式Euler格式。

2 计算结果与分析

2.1 网格独立性验证

欧拉-拉格朗日框架下的喷雾数值计算结果与网格大小有密切关系,因此需要验证网格独立性。为了评估喷雾性能对网格的依赖性,对无反应情况的Spray A采用4种不同的二维轴对称非均匀结构网格进行数值模拟,网格信息如表3所示。Nordin等[13]发现网格依赖性主要受径向(即垂直于喷射方向)上的单元网格尺寸的影响,如果径向上的单元网格尺寸太大,在液体雾化区域内得到的气体速度分布将是平坦的,较细的单元网格可以更准确地表示速度场,然而,喷射方向上的单元网格尺寸对液体蒸汽穿透长度和火焰浮升高度有很大影响,因此在计算域网格划分时,纵横比不能太大。

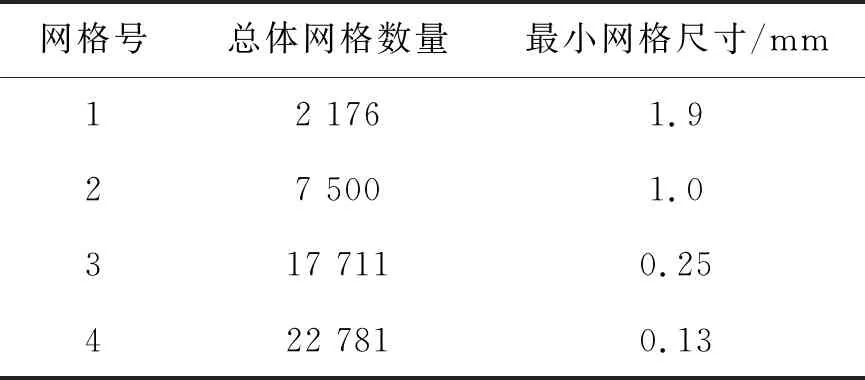
表3 二维网格信息

4种网格对液体穿透长度和蒸汽穿透长度数值模拟结果与SNL试验结果进行对比,如图4所示,发现随着网格尺寸减小,液体穿透长度增大,但当网格数量达到一定数量时,再细化网格却不增加液体颗粒包时,不会获得更好的模拟结果,只会增加计算成本。另外,对于液体穿透长度,mesh3和mesh4与试验结果有很好的一致性,说明网格最小尺寸为0.25 mm时,数值结果已经能够对喷雾性能做出较为准确的预测,这也验证了对三维网格的划分精度足够,不会对模拟结果造成影响。

图4 不同网格下液体和蒸气穿透长度

2.2 无反应情况射流喷雾性能

为了评估当前的湍流和喷雾模型设置,本文针对无反应情况Spray A,对数值模拟的液体和气体穿透长度、燃料混合分数分布结果与SNL试验数据进行对比验证。图5分别显示了液体和蒸气穿透长度随注入时间变化的试验与模拟结果,在本文中,液体穿透长度定义为从喷嘴出口到累积注入燃油总质量95%的最远液滴位置的轴向距离。与试验数据相比,该喷雾模型很好地预测了液体和蒸气穿透长度,只是在燃油注入早期液体和蒸气穿透长度与试验有很小的偏差,这是由于该喷雾模型不能很好反映燃油初次雾化造成的。

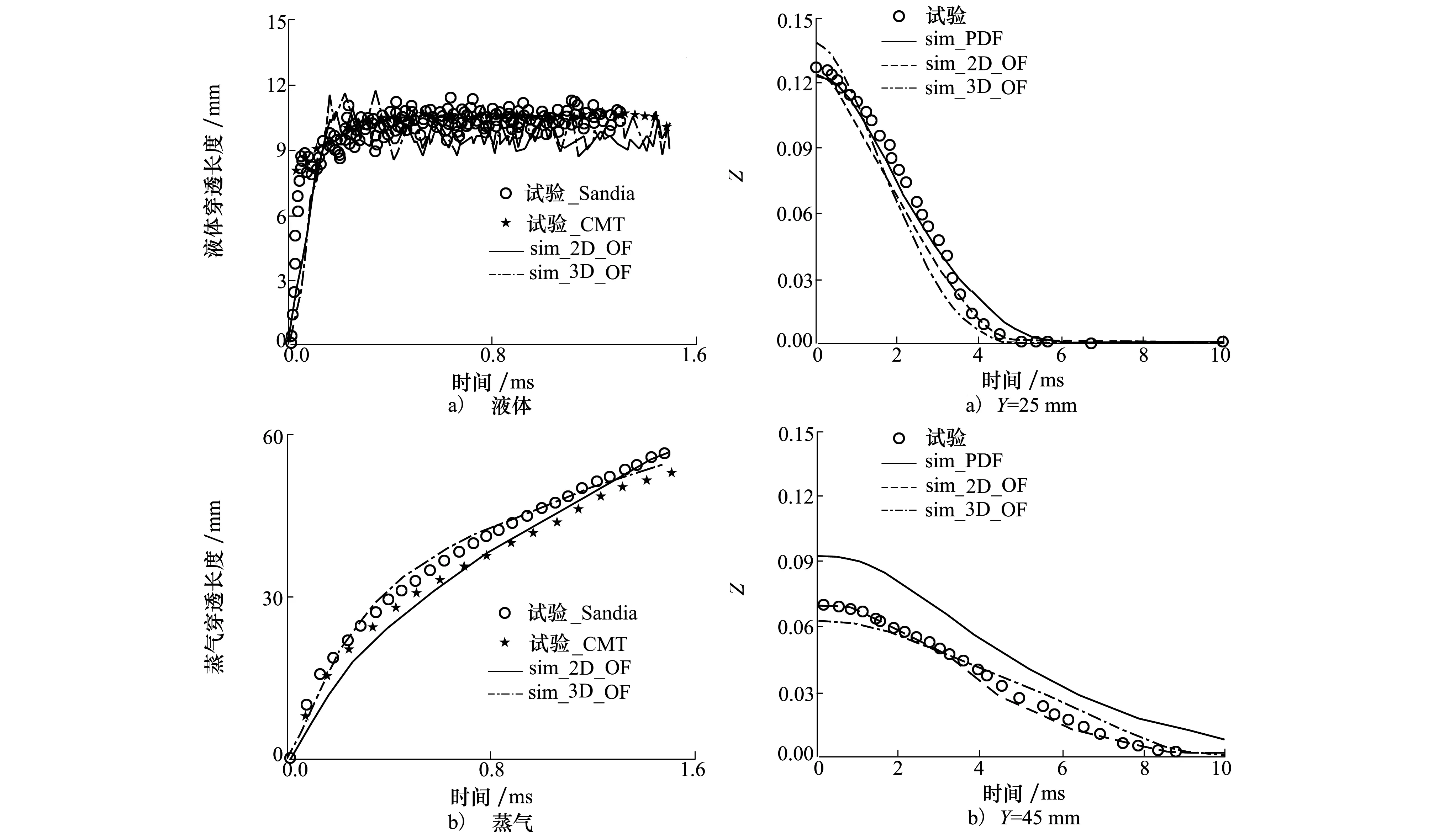
图5 无反应情况下液体和蒸气穿透长度图6 混合分数径向分布

燃料混合分数的准确分布对喷雾燃烧的点火延迟时间和火焰浮升高度的预测至关重要。在2个轴向位置(25 mm和45 mm)提取燃料混合分数Z,模拟结果与试验结果进行比较,如图6所示。可以看到模拟结果很好地预测了混合分数的径向分布,与试验结果有很好的一致性。只是在Y=25 mm处,预测结果略低于试验结果,但偏差值在试验误差范围内。

2.3 喷雾点火过程

通过分析有反应情况下的Spray A数值模拟结果研究燃油雾化后点火过程,图7显示了有反应情况下在燃烧室内压力升高随时间变化的曲线,其中蓝色虚线表示本文模拟得到的燃烧室压力升高随时间的变化曲线,绿色实线表示将蓝色曲线数据乘修正系数0.42得到的修正压力升高曲线,这是由于在试验中燃烧室是边长为108 mm的立方体,而模拟中为了降低计算成本,只关注中心射流及其雾化的计算域,从而将计算域简化为底面边长为70 mm的正方形,高为108 mm的长方体,体积的变化导致密度改变,所以得到的压力升高曲线斜率要远远大于试验数据曲线斜率;因此,假设燃油蒸发后迅速扩散,即燃烧室内气体密度均匀,根据连续方程和理想气体状态方程得到

(6)

式中:ρ1,A1分别为假设模拟燃烧室气体密度和底面积;ρ,A为假设试验燃烧室气体密度和底面积。

从图7中看到,燃油通过压力旋流喷嘴不断被注入燃烧室,由于高压(150 MPa)和较高的环境温度(900 K),燃油迅速雾化蒸发,在t<0.43 ms这一过程,只是发生燃油雾化蒸发和低温反应,释放热量小,压力几乎没有发生变化;在0.43 ms时燃油自燃,在随后的时间中,由于燃烧放出大量热量,燃烧室内压力随时间单调增加;在主燃烧阶段,燃油蒸汽与空气混合控制火焰的传播;修正压力升高曲线与试验数据有很好的一致性,点火延迟时间也得到了很好的预测。

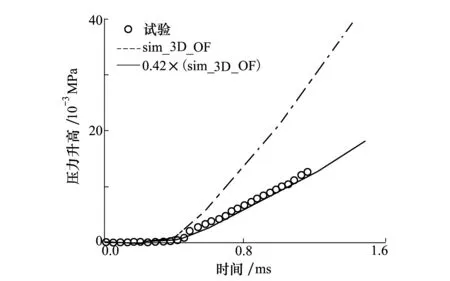
图7 压力升高曲线

图8显示了无反应情况和有反应情况下不同时刻混合分数分布云图,其中黄色实线为当量混合分数等值线(Zst=0.045),对于有反应情况,0.4 ms是燃油高温点火之前时刻,1.5 ms为燃油燃烧后一时刻。发现高温点火前2种情况下的喷雾径向扩散基本相同,随后,在轴向和径向上,反应喷雾情况下的混合物分数比无反应情况下(图中为1.5 ms)扩散到更大的区域。这是由于反应情况下的径向速度高于无反应情况下的径向速度,这使得燃料蒸气在径向上的传输更快;反应情况下的,高温热气的膨胀加速了喷雾的径向扩散速度,这也使得反应情况下蒸气穿透长度更长。

图8 混合分数分布云图

图9显示了反应情况下不同时刻气体温度云图,黄色实线表示当量混合分数等值线,从中可以看到在反应前即0.4 ms时刻,气体最高温度约为1 200 K,初始燃烧室内环境温度为900 K,这表明在燃烧前燃烧室内已经进行了低温放热反应;在0.5 ms时刻,已经发生燃烧,可以看到在距离燃油喷嘴下游约为20 mm处形成一个高温火核,该火核以当量混合分数等值线为中心温度逐渐向四周扩散降低,火核随后长大,火焰沿着化学当量混合分数线传播,在下游化学当量混合分数周围形成高温区,表明混合控制扩散火焰建立。

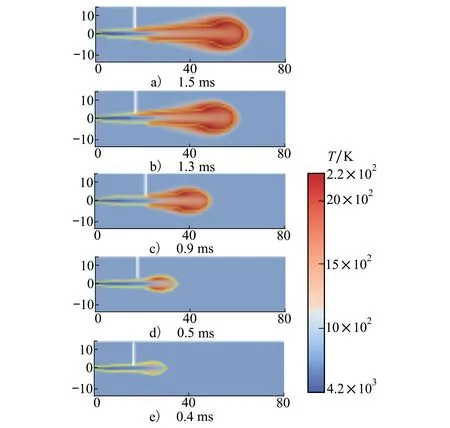
图9 不同时刻温度云图

另外,发现扩散火焰并没有附着在燃油喷嘴附近,而是在化学当量混合某处下游被点燃,表现为火焰浮升一定高度,火焰浮升高度随时间有轻微波动,不同时刻火焰浮升位置在图中用白色实线表示出来;火焰浮升高度是指燃油喷嘴与最靠近喷嘴的火焰前缘之间距离,试验中通常使用激发态OH基达到最大值50%的位置定义火焰浮升高度,采用化学发光法测得,本文采用温度达到1 600 K作为判断标准。从图9看到,火焰建立是在约距离喷嘴下游20 mm处,随后,火焰稳定在距离喷嘴下游17 mm处,将不同时刻火焰浮升高度进行平均,得到平均火焰浮升高度为17 mm,这与SNL试验得到16.4 mm几乎一致,得到很好预测。这表明该喷雾燃烧模型很好地模拟了燃油点火过程中的瞬态行为和火焰浮升现象。

为了进一步说明喷雾燃烧点火过程,图10给出了几个关键组分质量分数分布云图,其中黄色实线表示化学当量混合分数等值线,上文通过不同时刻温度云图得知,在雾化蒸发燃油蒸气未被点燃前,燃烧室已经发生了反应,气体温度升高;确实如此,有反应情况的喷雾点火经历2个阶段,第一阶段为低温点火阶段,如10a)图和图10b)所示,从0.3 ms到0.4 ms这一时间段内,酮过氧化氢(ketohydroperox-ide,KET,在这指OC12H23OOH)质量分数迅速降低,而H2O2含量迅速升高表示第一阶段低温点火开始[15];从0.4 ms到0.5 ms这一时间段内,如图13中b)和c)所示,H2O2质量分数降低,OH含量上升表示第二阶段高温点火已经开始;在1.5 ms时刻,从OH分布可知,火焰沿着化学当量混合区域传播,另外,值得注意的是,四副图的右半为H2O2质量分数分布云图,即使在高温点火后,在靠近燃油喷嘴的化学当量混合分数区域内,H2O2仍然存在且含量变化不大,说明在高温点火后,低温点火会持续稳定进行。

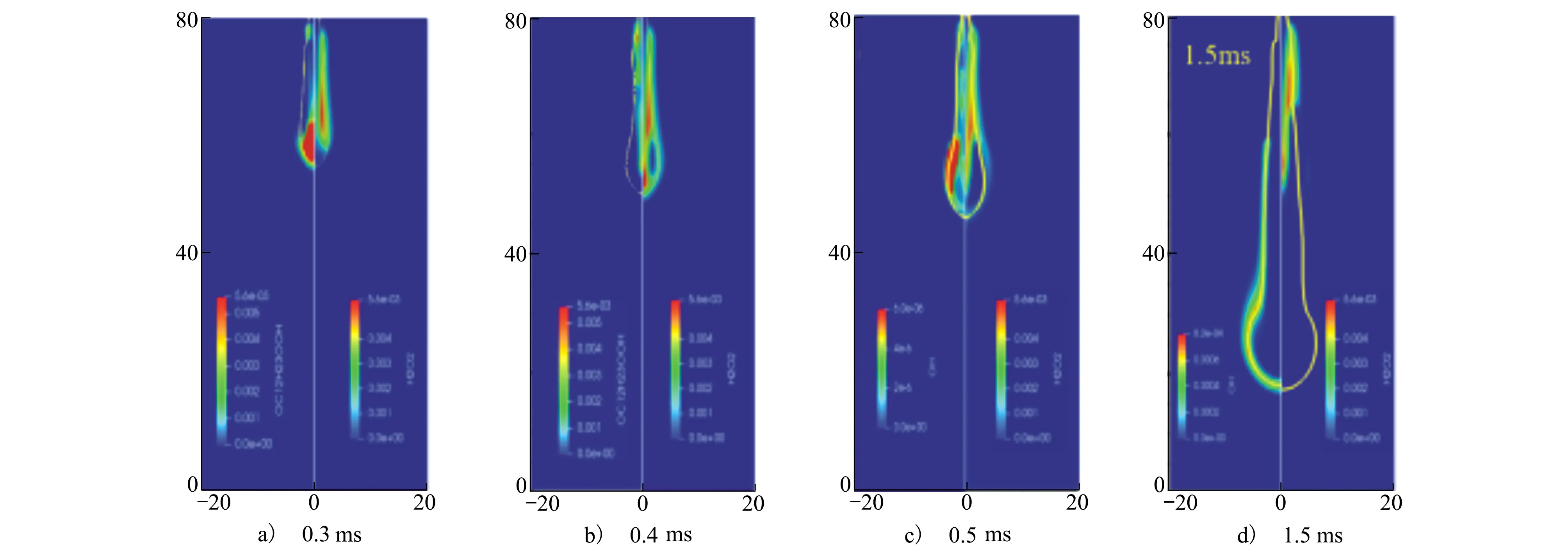
图10 不同组分质量分数分布云图

图11显示了在有反应和无反应2种情况下流场中温度随局部混合分数分布散点图。对于无反应喷雾情况,混合分数空间内的温度分为两部分,第一部分沿着红色虚线密集分布,第二部分在红色虚线下方,与第一部分相交于流场中混合分数的最大值处,此处的温度约为585 K,此温度为当前环境压力下(约6 MPa)燃油的沸腾温度;第一部分中的燃油蒸气来自于燃油喷嘴出口附近油滴在沸腾温度下的蒸发,由于蒸发的吸热作用,当燃油与高温空气混合时,局部温度会随着混合分数的增加而降低。第二部分中的燃油蒸气来自于温度低于沸点的油滴,这些油滴的蒸发速率随着温度的升高而增加,因此在第二部分的燃油蒸气局部混合分数也随着温度升高而变大。

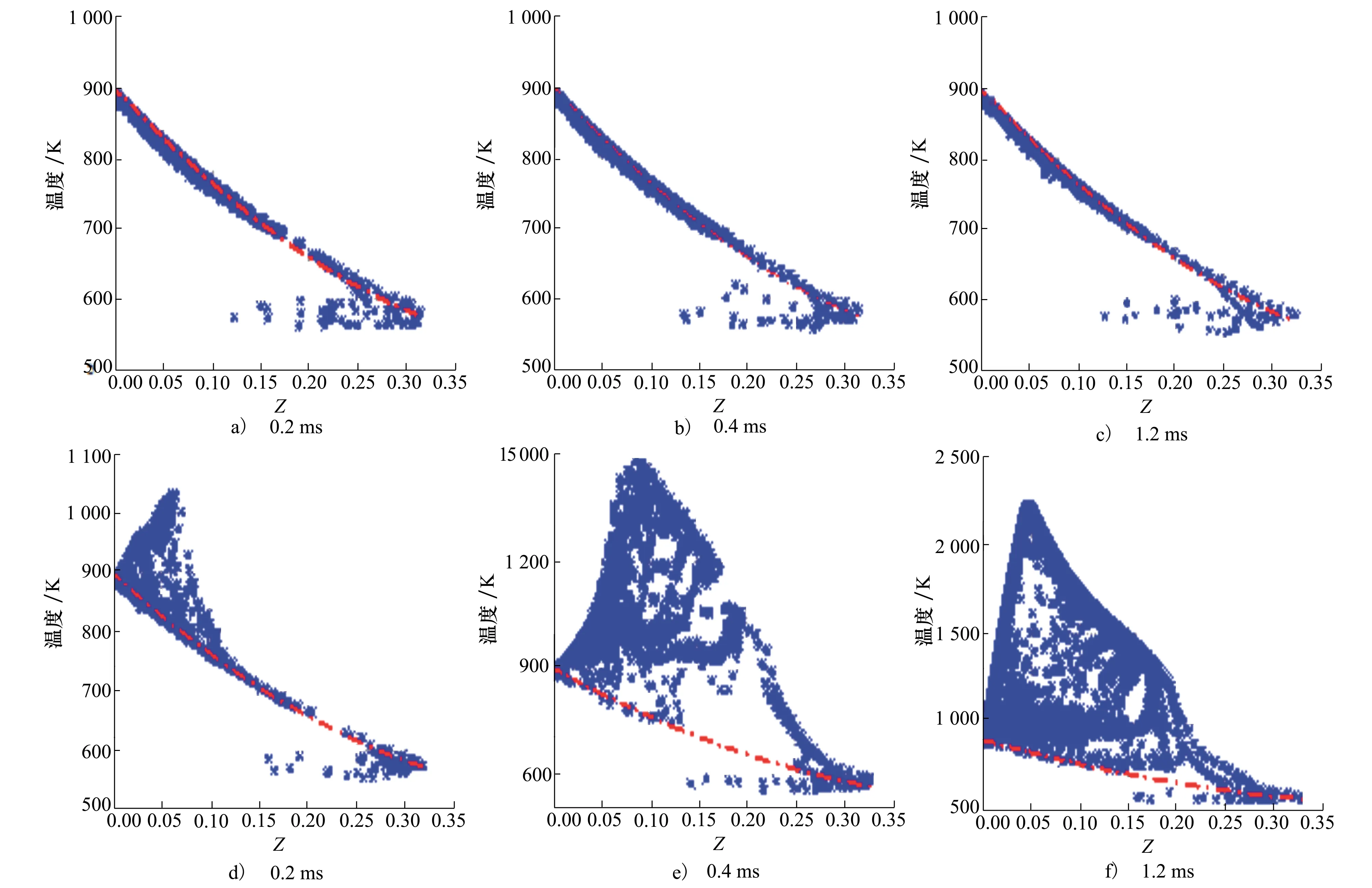
图11 流场温度随混合分数分布散点图

在无反应喷雾情况下,不同时刻流场温度分布变化不大,对于无反应喷雾情况,Mastorakos等[15]使用一个二次函数来拟合流场温度与混合分数之间的关系

T=1 500Z2-1 500Z+Tam

(7)

式中:Z为混合分数,Tam为环境初始温度,此算例中为900 K。

图11中所有为红色虚线为温度与混合分数的二次函数解析拟合,该温度与混合分数的关系与气态燃料中不同,一般情况下,如果气态燃料路易斯数(Lewis number)与该燃油蒸气的路易斯数相同时,气态燃料射流温度与混合分数为线性关系,这种差异是由于燃油喷雾蒸发吸收了大量热量,造成热量损失造成的。

对有反应喷雾情况,在反应初期(0.2 ms),2种情况的流场温度分布差别很大,在有反应情况下此刻进行低温反应,将有反应情况的散点图与无反应情况的拟合函数曲线进行比较,发现有反应情况在低温反应开始前混合物的温度分布与无反应情况下的相似;在0.4 ms时,混合物分数高于0.05的大多数混合物温度在1 000～1 500 K之间,这说明低温反应在此已经充分发展;1.2 ms 时的散点图表明,此时流场可分为两部分,从火焰浮升高度位置分开,火焰浮升高度上方(温度高于1 200 K)流场中的燃烧呈现典型的扩散火焰结构,其温度最大值对应的化学计量混合分数为0.045,火焰浮升高下方流场中的燃烧显示出充分发展的冷焰(cool flame)结构。

2.4 注入压力对点火延迟时间和火焰浮升高度的影响

图12显示了在不同燃油注入压力下,点火延迟时间和火焰浮升高度的变化曲线,研究了注入压力分别为50,100,150 MPa的3种情况。除了燃油注入压力不同外,其他试验条件均相同,环境温度900 K,环境气体组分与表2有反应情况相同。可以看到,模拟较好地预测了点火延迟时间和火焰浮升高度趋势,但在3种情况下,模拟的点火延迟时间预测均稍高于试验数据,这可能与计算网格有关,本文所使用的网格预测到的混合分数要稍低于试验数据,混合分数对点火延迟时间和火焰浮升高度的精准预测非常重要,这可能是导致在不同试验条件下,模拟点火延迟时间均高于试验数据的原因。

图12 注入压力对点火时间和火焰浮升高度的影响

点火延迟时间和火焰浮升高度这两个参数对注入压力的变化并不敏感,总的趋势是随着注入压力的升高,点火延迟时间降低,火焰浮升高度有所上升;但我们看到,不同的燃油注入压力对应的点火延迟时间在0.5 ms附近,相邻2个不同的注入压力之间点火延迟时间相差小于0.05 ms, 这也导致火焰浮升高度变化不大;有趣的是,注入压力升高,点火延迟时间降低,火焰浮升高度却有所升高,通常来讲,点火延迟时间降低,火焰浮升高度也会降低,但在这正好相反,这是由于注入压力升高,燃油雾化蒸发速率变大,第一阶段的低温反应能够更快开始,点火延迟时间也会降低,但注入压力的升高会给燃油液滴更高的初始动量,这就使得低温反应和高温点火在距离燃油喷嘴更远的地方发生,即表现为火焰浮升高度的升高。