用几何画板 教漂亮数学

陈燕萍

[摘 要]几何画板是一款动态几何工具，适用于数学的分析、作图等，它有强大的作图与动画等功能.几何画板技术与数学课堂教学深度融合，能使静态的数学图形运动起来，能展示数学的动态之美、直观之美、图形之美、逻辑之美，激发学生学习数学的兴趣，有助于发展学生的数学核心素养，打开数学课堂教学的另一扇窗.文章运用几何画板，探索数学课堂教学与信息技术深度融合的方式.

[关键词]几何画板;信息技术;数学课堂教学

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2021）17-0012-03

数学是一门集数形关系知识于一身的学科，很多的数学课堂教学，还是以粉笔、三角板（圆规）等工具开展讲授、板书等主要的教学活动，往往只能呈现变化过程中的某一静止状态，不容易挖掘数与形之间的关系，发现它们的变化规律，学生感觉数学学习很困难，教师感觉数学教学很辛苦.

信息技术与课堂教学深度融合，为学生提供丰富的资源，让课堂学习变得有趣一点，轻松一些，对调动学生的学习积极性有重要作用.几何画板是一款动态几何工具，适用于数学的分析、作图等.本文尝试运用几何画板探索数学课堂教学与信息技术深度融合的方式：借助几何画板强大的图形处理和动画处理功能，探索数与形之间的关系，展示数学的动态之美、直观之美、图形之美、逻辑之美，让数学运动起来，使问题化难为易，激发学生学习数学的兴趣，发展学生的数学核心素养，打开数学课堂教学的另一扇窗.

一、运用几何画板，探究几何定理、概念的形成过程，发展学生的思维能力

数学课程标准中指出：数学教材内容要呈现数学知识的形成过程.在教学过程中，可以运用几何画板探究概念的形成过程.运用几何画板指导学生动手操作，指导学生观察现象，度量、统计与分析数据，归纳总结各种情况，打破了传统的“教师讲授—学生练习—强化记忆—测试讲评”的教学模式，改变为“问题—实验—观察—猜想—证明—应用”的新探究模式.通过系列探索，容易开阔思路，发展思维，提升素养.

例如，《平行线分线段成比例定理》一课的学习难度大，学生理解、记忆及应用都比较困难. 如果让学生动手进行测量、计算、归纳，需要大量的时间，所以许多教师在上这一课时，都会直接告诉学生结论，让学生生硬记忆，或者花上很多时间进行探究，效果并不理想.但是通过几何画板的测量、计算等功能，直观地展示测量与计算结果，就能吸引学生眼球，促进学生积极参与课堂活动和思考，使得教学任务轻松愉快地完成，并达到让学生长时间记忆不忘记的目的.

教学时，先出示图形与题目“已知：[L1∥L2∥L3]，探究[AB]∶[BC]与[DE]∶[EF]的关系”.运用几何画板作出测量与计算（如图1），不断拖动平行线及两条截线的位置，观察数据.

学生发现：只要平行条件不变，无论如何变换不同的位置，两组线段的比值始终都是相等的.由此得到的结论，学生学得轻松，记得牢固.接着再次改变图形，让点A与D重合（如图2），结论同样成立.再次移动：让点B、E重合（如图3），结论同样成立.

再变：把平行线L1、L2、L3隐藏，分别得到图4、图5，又发现了什么？

这样通过几何画板，打开数学几何探究课堂教学的另一扇窗，学生通过操作探索发现计算结果与图形变化无关，容易掌握图形变换的规律，享受学习数学的快乐与感受数学的神奇.苏霍姆林斯基说过：“在人的心灵深处，都有一种根深蒂固的需要，就是希望自己是一个发现者、研究者、探索者，而在儿童的精神世界中，这种需要特别强烈.”有了强烈的求知欲望，学习数学就转变为学生的自主行为了！

二、用几何画板揭示变化的图形中不变的几何规律，感受图形之间各种量的关系

几何就是在不断变化的几何图形中研究不变的几何规律.而几何画板工具的精髓就是“在运动中保持给定的几何关系”，正好为几何学习研究提供了技术支持.

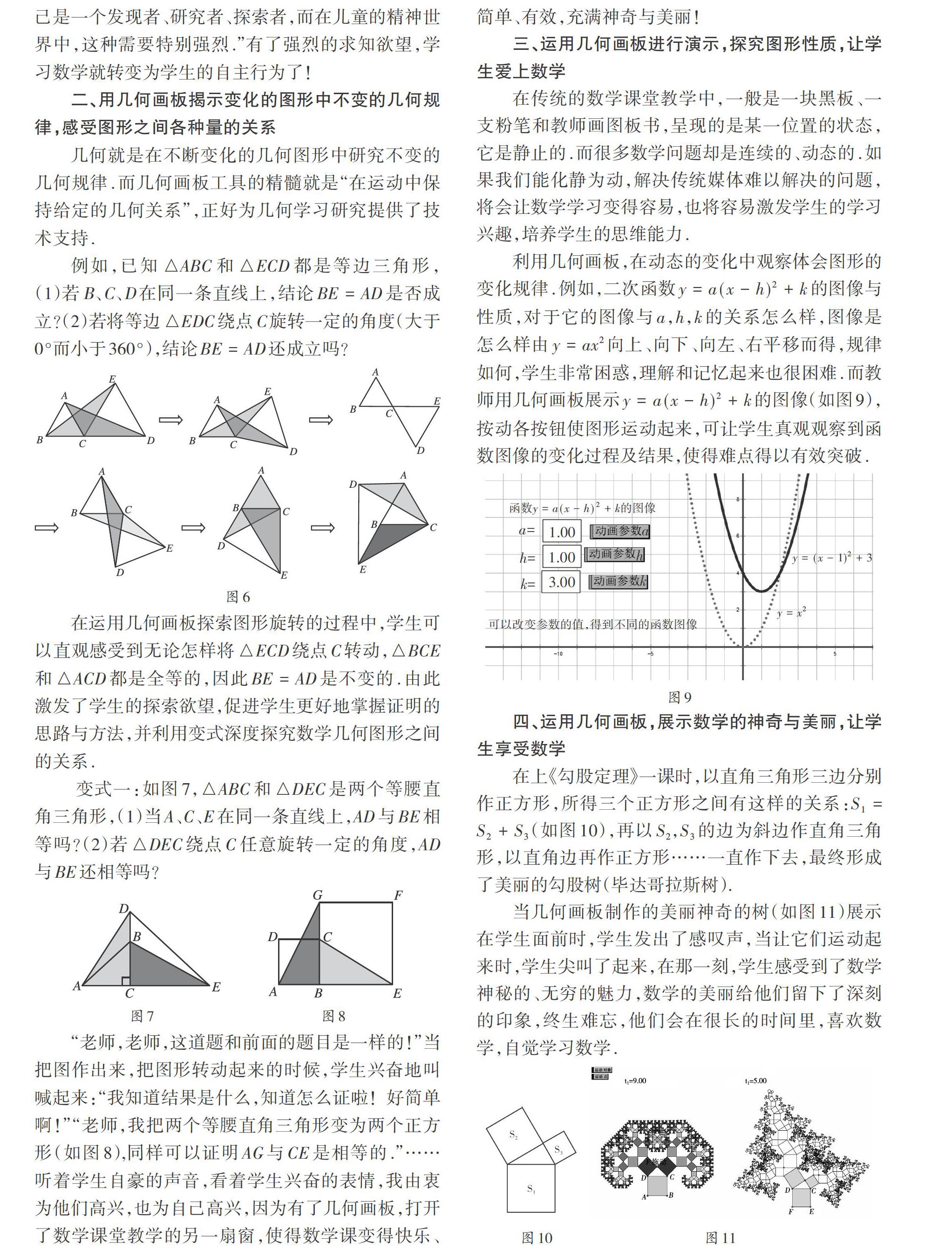
例如，已知[△ABC]和[△ECD]都是等边三角形，（1）若B、C、D在同一条直线上，结论[BE=AD]是否成立？（2）若将等边[△EDC]绕点C旋转一定的角度（大于0°而小于360°），结论[BE=AD]还成立吗？

在运用几何画板探索图形旋转的过程中，学生可以直观感受到无论怎样将[△ECD]绕点C转动，[△BCE]和[△ACD]都是全等的，因此[BE=AD]是不變的.由此激发了学生的探索欲望，促进学生更好地掌握证明的思路与方法，并利用变式深度探究数学几何图形之间的关系.

变式一：如图7，[△ABC]和[△DEC]是两个等腰直角三角形，（1）当A、C、E在同一条直线上，[AD]与[BE]相等吗？（2）若[△DEC]绕点C任意旋转一定的角度，[AD]与BE还相等吗？

“老师，老师，这道题和前面的题目是一样的！”当把图作出来，把图形转动起来的时候，学生兴奋地叫喊起来：“我知道结果是什么，知道怎么证啦！好简单啊！”“老师，我把两个等腰直角三角形变为两个正方形（如图8），同样可以证明AG与CE是相等的.”……听着学生自豪的声音，看着学生兴奋的表情，我由衷为他们高兴，也为自己高兴，因为有了几何画板，打开了数学课堂教学的另一扇窗，使得数学课变得快乐、简单、有效，充满神奇与美丽！

三、运用几何画板进行演示，探究图形性质，让学生爱上数学

在传统的数学课堂教学中，一般是一块黑板、一支粉笔和教师画图板书，呈现的是某一位置的状态，它是静止的.而很多数学问题却是连续的、动态的.如果我们能化静为动，解决传统媒体难以解决的问题，将会让数学学习变得容易，也将容易激发学生的学习兴趣，培养学生的思维能力.

利用几何画板，在动态的变化中观察体会图形的变化规律.例如，二次函数[y=a（x-h）2+k]的图像与性质，对于它的图像与a，h，k的关系怎么样，图像是怎么样由[y=ax2]向上、向下、向左、右平移而得，规律如何，学生非常困惑，理解和记忆起来也很困难.而教师用几何画板展示[y=a（x-h）2+k]的图像（如图9），按动各按钮使图形运动起来，可让学生真观观察到函数图像的变化过程及结果，使得难点得以有效突破.

四、运用几何画板，展示数学的神奇与美丽，让学生享受数学

在上《勾股定理》一课时，以直角三角形三边分别作正方形，所得三个正方形之间有这样的关系：[S1=S2+S3 ]（如图10），再以[S2]，[S3]的边为斜边作直角三角形，以直角边再作正方形……一直作下去，最终形成了美丽的勾股树（毕达哥拉斯树）.

当几何画板制作的美丽神奇的树（如图11）展示在学生面前时，学生发出了感叹声，当让它们运动起来时，学生尖叫了起来，在那一刻，学生感受到了数学神秘的、无穷的魅力，数学的美丽给他们留下了深刻的印象，终生难忘，他们会在很长的时间里，喜欢数学，自觉学习数学.

五、運用几何画板，使问题化难为易

很多数学问题难在知识的推理过程，动态的几何问题，轨迹问题更是如此.合理运用几何画板的作图及轨迹的追踪功能，可以直观形象地演示复杂图形的形成过程及知识的推导过程，使问题由繁变简，化难为易，从而有利于突破教学难点.

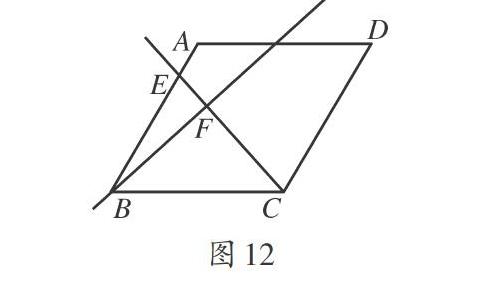
例如，2017年中考真题：如图12，在菱形[ABCD]中，[∠ABC=60°]，[AB=4]，点[E]是[AB]边上的动点，过点[B]作直线[CE]的垂线，垂足为[F]，当点[E]从点[A]运动到点[B]时，点[F]的运动路径长是多少？

本题中，求点[F]的运动路径长，先要知道点运动的轨迹是什么，这是学生最难想象与理解的地方，画出图形就是解题的难点与关键所在.通过几何画板的演示，可以非常清晰地知道点运动的轨迹是以[BC]为直径的圆上的一段弧，再由作图的条件与过程分解，引导学生理解分析为什么是这样的一段弧.当没有几何画板辅助时，可以怎样思考作出图形，由此轻松突破了难点（如图13），余下的计算就比较简单了.

使用几何画板进行数学教学及实现多媒体与课堂教学的深度融合，通过具体的感性的信息呈现，能够把知识发生与发展的过程合理展示，与学生思维发展规律、认知特点相吻合，给学生留下更深刻的印象，激发学生积极参与学习过程.

古人有云“横看成岭侧成峰”，角度不同，看到的风景也不同.传统教学自有传统教学之美，用几何画板进行的几何课堂教学，打开了数学课堂教学的另一扇窗.用几何画板，教漂亮数学，让我和学生感受到了数学课堂的另一种魅力，那是一种自由、开放、灵动之美！

（责任编辑 黄桂坚）