基于扰动观测器的伺服控制律设计方法研究
2021-07-10黄子露付志敏高小雨张丛丛
黄子露,付志敏,高小雨,张丛丛
(航空工业洪都,江西 南昌,330024)
0 引言
伺服系统是用来控制被控对象的某种状态,使其能够自动的、连续的、精确的复现输入信号的变化规律的随动系统。伺服系统作为目前飞行器机动飞行的主要执行机构,其动态性能对飞行器至关重要。而决定伺服系统动态性能的,除了伺服系统硬件固有特性外,控制律对其影响也十分重大。
伺服系统常用的控制律设计方法为PID控制,该方法成熟可靠,简单易懂[1]。本文提出了基于扰动观测器的伺服控制律设计方法,较之PID控制,该方法能更直观的看出控制律中各部分所代表的含义。
1 伺服控制律设计原理
1.1 直流电机模型
直流电机模型框图如图1,Ua为线圈输入电压;ia为线圈电流;Tg为电磁转矩;TL为外界负载;ω为电机输出轴角速度;θ为电机输出轴角位移;Ra为线圈电阻;La为线圈电感;K为电磁转矩系数及感应电动势系数;J为转子惯量;f为转子动摩擦系数。
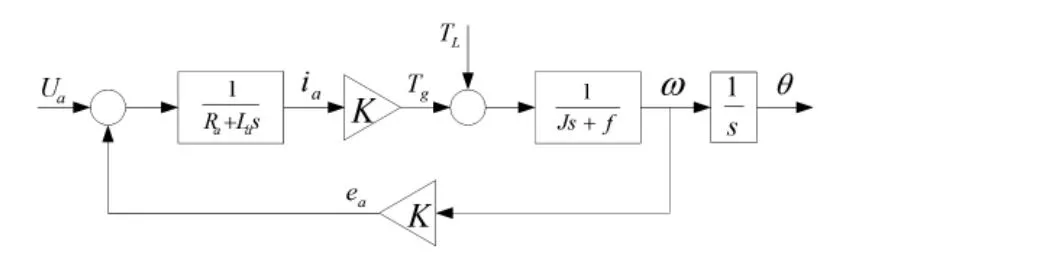
图1 直流电机模型框图[2]
1.2 扰动观测器
扰动观测器模型框图如图2,R为输入;D为外界扰动;Y为输出;(D为估计扰动;ξ为测量噪声;P为系统模型;Pn为标称模型;Q为滤波器模型。

图2 扰动观测器模型框图[3]
过推导可得

由式(2)可得
当Q→0GRY=P GDY=P GξY=0
当Q→1GRY=Pn GDY=P GξY=-1
测量噪声ξ相对于输入指令R、外部扰动D来说是一个高频信号,因此对于该扰动观测器,只要Q是一个低通滤波器,即可实现

1.3 基于扰动观测器的伺服控制律设计
针对图1,推导直流电机传递函数表达式
从电压输入到电机输出轴角速度的传函:
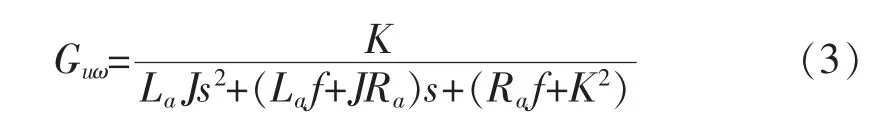
从负载力矩到电机输出轴角速度的传函:

基于扰动观测器的闭环电动伺服系统框图如图3。

图3 基于扰动观测器的闭环伺服系统
其中

伺服控制器的设计问题转化为滤波器Q、标称模型Pn的选择问题。
参照图1,实际使用的直流电机中,电磁时间常数远小于惯性时间常数,转子惯量远小于电势系数。此时,将直流电机从输入电压到输出角速度的模型近似为一个惯性环节,其时间常数近似为J*Ra/K2。
由上一章节结论可得,标称模型Pn即近似为闭环系统模型,在确定标称模型Pn时,可以初步考虑选取其带宽为左右。考虑到Q的带宽直接影响系统的开环增益,带宽越大,开环增益越大,所以在确定滤波器Q时,要综合考虑闭环系统的稳定性。
2 模型不确定性的稳定性分析
考虑到G1G2含积分环节,而期望的标称模型Pn不可能含积分环节,令

Δ为模型G与Pn的乘性误差。
图3所示的系统框图经线性分式变换后,其模型框图如图4所示。

图4 闭环伺服系统线性分式变换模型框图
其中,

图4的模型框图可简化为图5。
图5 图4的简化框图
其中,

根据小增益定理,为使系统在误差?存在的情况下稳定,则需满足

式(9)给出了基于扰动观测器设计伺服控制律时Q和Pn相互约束:的大小体现了标称模型Pn和真实模型G的差异,由于标称模型Pn体现了我们对闭环系统性能的期望,在确定了标称模型Pn后,Δ实际已经确定了;为了使闭环系统在实际模型有限不确定性的情况下一直稳定,必须对Q进行限制,Q为低通滤波器,‖QΔ‖∞的大小与Q的带宽密切相关。
3 基于扰动观测器的伺服系统仿真
选取市面上一款直流电机,参数如下:

综合式(5)、(6)、(7)计算出G的表达式,选取期望的标称模型,可以画出Δ的BODE图,如图6所示。

图6 Δ的增益曲线
根据式(8)、(9)的约束可以大致对Q的带宽进行约束,在此选择Q=1/(0.001s+1),综合画出Δ和Q得BODE图,如图7所示。
从图7可以看出,Q满足式(9)的稳定性条件。
针对选取的直流电机参数和控制器参数对闭环系统进行仿真,在0.1s加入幅值为1的阶跃输入,0.3s加入幅值为0.1的阶跃负载,对比标称模型Pn的阶跃响应如图8所示。
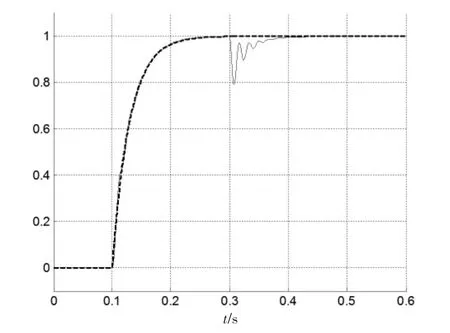
图8 闭环系统阶跃响应曲线
图8中的虚线为标称模型的阶跃响应,实线为实际闭环系统按上述仿真条件的响应。可以看出,该闭环系统与标称模型相似度很高,对外界负载扰动的抑制效果也很好,证实了基于扰动观测器设计的伺服控制器是有效可行的。
4 结语
本文采用的基于扰动观测器的控制器设计方法,将经典的频域控制器各个部分进行了分离处理,使得控制器各个部分物理含义更加明了直观。对于控制器的设计过程,工程人员能够将闭环系统期望的状态直观的体现在控制器设计上。
