基于现代控制理论的飞机横航向控制律设计研究

刘诗超，翁雪花，邹俊俊，冷国旗

（1.海装驻南昌地区军事代表室，江西 南昌，330024;2.航空工业洪都，江西 南昌，330024）

0 引言

对于电传飞机而言，飞行控制系统相当于人类的大脑，是至关重要的，而控制律设计作为飞行控制系统中的关键技术之一，受到设计人员的高度重视。

目前在工程实践中使用的控制律设计方法，为调参法。控制律一般采用PID结构，参数设计采用极点配置方法、根轨迹分析法等较为经典的方法。随着新型飞行器的不断出现，控制律设计所面临的挑战不断增加，现代控制理论和方法的应用研究越来越受到关注和重视。

本文研究几个具有工程应用前景的控制方法：线性二次型最优控制方法、特征结构配置方法和动态逆方法。

1 控制律设计

本文以某型教练机5km、0.3M状态点为例，应用线性二次型最优控制方法、特征结构配置方法及动态逆方法对飞机横航向控制律设计进行研究。

1.1 线性二次型最优控制方法

线性二次型最优控制方法的研究始于20世纪60年代，是一种最优控制系统设计方法。该方法以线性系统为对象，取状态变量和控制变量的二次型函数的积分作为性能指标函数，寻找状态线性反馈控制律，使得性能指标函数最优。该方法能生成一个简单的状态反馈控制律，易于计算和工程实现。

1.1.1 方法描述

对于系统

其中，x为n维状态向量；u为r维输入向量，y为m维输出向量；A为n×n维的常数矩阵、B为n×r维的常数矩阵、C为m×n维的常数矩阵、D为m×r维的常数矩阵。

其状态反馈控制律为

假设能控且可观的线性定常系统，设计最优控制律u（t），使得性能指标J取极小值：

其中，Q为n×n维半正定的状态加权矩阵、R为r×r维正定的控制加权矩阵，常选为对角线矩阵。

根据线性最优控制理论，使得J取极小值的控制律u（t）存在且唯一地由式（4）确定：

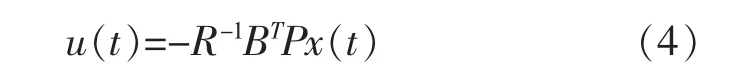
式中，P为对称矩阵，且满足黎卡提（Riccati）方程：

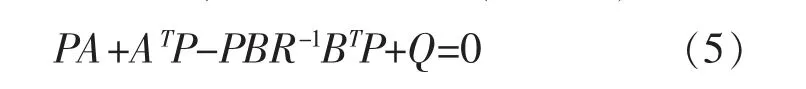
则控制系统的全状态反馈增益K计算如下：

1.1.2 设计

针对飞机横航向控制律的设计，选取状态变量x=[βωxωyγ]，n=4，控制输入为u=[δxδy]，得到相对应的飞机状态空间表达式。

首先验证系统的能控能观性。

对多输入系统，其能控的充分必要条件是能控性矩阵

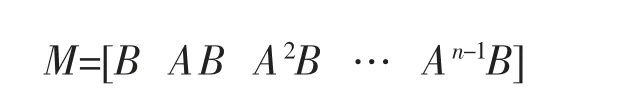
的秩为n。

其能观的充分必要条件是能观性矩阵

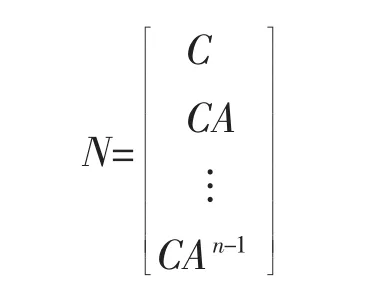
的秩为n。

通过上述判据，验证0503状态点的状态方程具有能控能观性，满足设计前提。

其次，要选取合适的加权矩阵Q和R。

Q和R是状态向量和输入向量的加权矩阵，两者取值与系统的性能相关，通过反复取值计算仿真，观察仿真结果，综合考虑系统动态性能指标，选取Q、R矩阵如下：

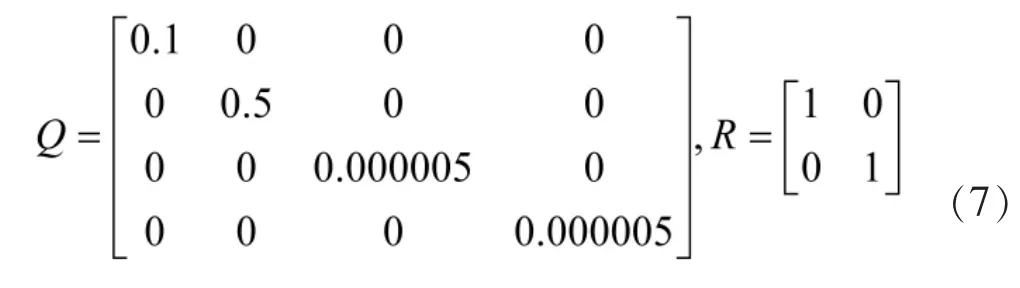
再由A、B、Q、R求解黎卡提矩阵微分方程，得到黎卡提矩阵P，由P求得反馈增益矩阵K。这里利用MATLAB工具箱提供的lqr()函数，调用格式为K=lqr（A，B，Q，R），可得到反馈矩阵K如下：

1.2 特征结构配置方法

特征结构配置方法是20世纪60年代发展起来的一种基于时间域的多变量系统设计方法。该方法根据要求选择适当的特征值和特征向量，使系统达到期望的动态响应特性，类似于经典控制理论中的零极点配置。在特征结构配置技术中，特征值用于闭环系统的稳定，特征向量用于动态响应的解耦，两者一起保证系统的动态性能。

1.2.1 方法描述

对于系统式（1），其状态反馈控制律为

则有

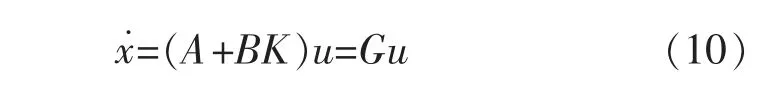
其中，K∈Rr×n、G∈Rn×n。若G具有n个互异特征值λi，i=1，2，K，n，对应的特征向量为vi，则有

特征结构配置方法即是寻找K，使得G即（A+BK）含有规定的特征值和特征向量。

1.2.2 设计

首先选择期望的特征值和特征向量。

依据GJB 185-86一级标准，选择荷兰滚特征根为-2.5±2.5i，对应的荷兰滚阻尼比为0.7071，荷兰滚频率为3.5355，滚转模态特征根为-3，对应的滚转模态时间常数为0.33，螺旋特征根为-0.002，对应的螺旋模态倍幅时间为500，则期望的特征值：

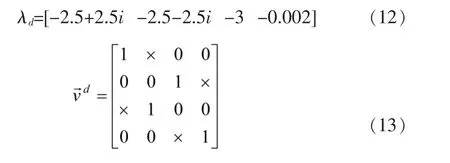
其中“×”表示未受约束（即任意的）项，而所有其他值（包括“0”）表示严格的特征向量约束。

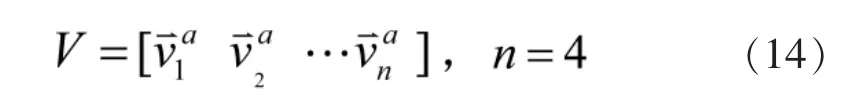
由于矩阵B的秩为r（r=2），小于n，引入线性变换T，使得B变换后的秩为n，则

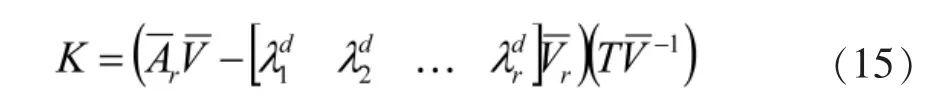
综上，通过计算，可得到基于特征结构配置的反馈矩阵K为

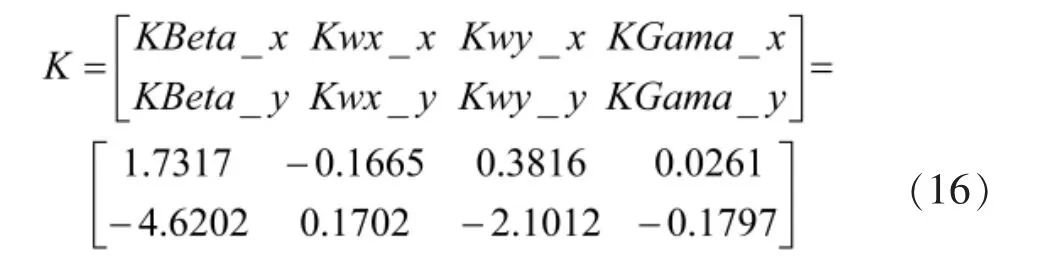
1.3 动态逆方法

动态逆方法又被称为“反馈线性法”，始于20世纪70、80年代，是建立在逆系统理论基础上的一种方法，其实质是用期望的动态环节，通过代数运算，替代原系统中存在的不符合期望的动态环节，使系统输出为期望的动态环节。

1.3.1 方法描述

假设有非线性系统

其中x是状态向量，u是控制向量。

假设g（x）可逆，则通过求逆，当控制律为

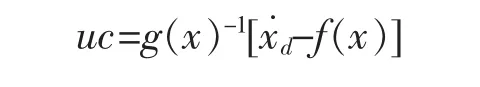
1.3.2 设计

根据横航向控制的目的，选择的控制变量为β和ωx，则飞机方程简化为

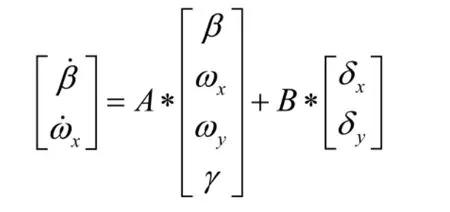
其中，A为4×4维常数矩阵，B为4×2维常数矩阵，则

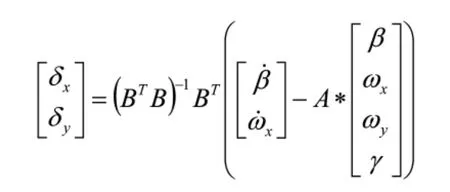
一般希望飞机响应为一阶惯性环节，因此这里构造期望的动态特性为

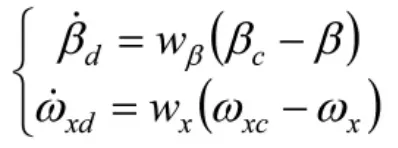
其中，βc和ωc为侧滑角和滚转角速率指令。

根据时标分离原则及快慢回路间带宽的选择要求，其带宽设计为wβ=2rad/s,wx=10rad/s，则有

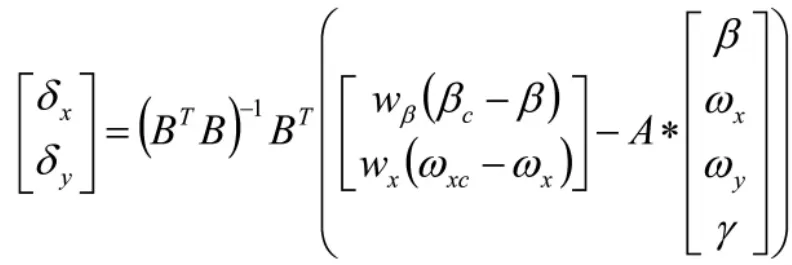
通过计算，可得基于动态逆方法的反馈控制律为

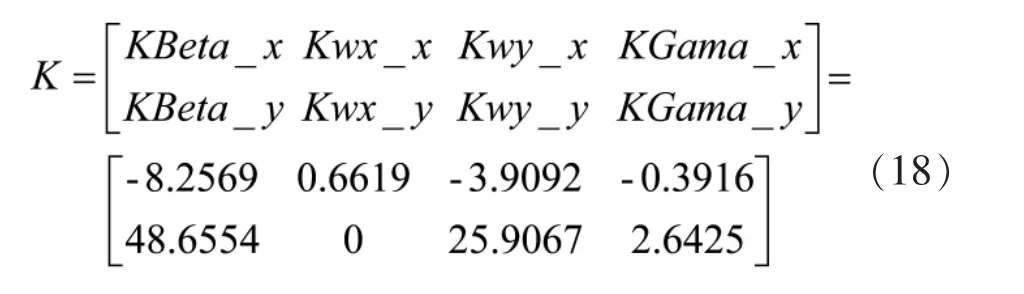
2 仿真分析

基于上述方法得到的控制律，在MATLAB Simulink下搭建模型，该模型包括控制系统、作动器和飞机方程，框图如图1所示。

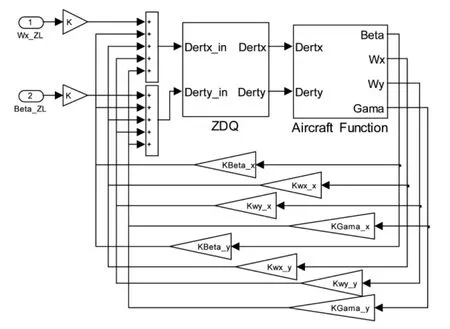
图1 仿真模型示意图

分别给出10°/s的滚转角速率指令和1°的侧滑角指令，三种方法仿真结果如图2、图3所示。

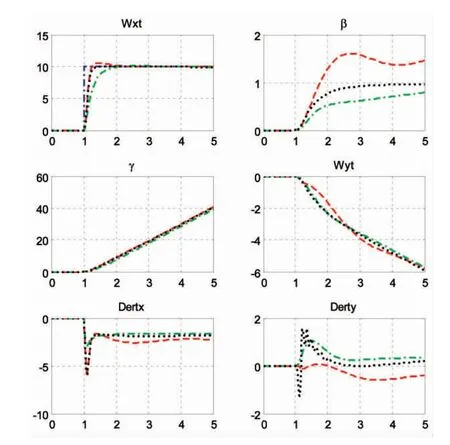
图2 横向仿真结果对比

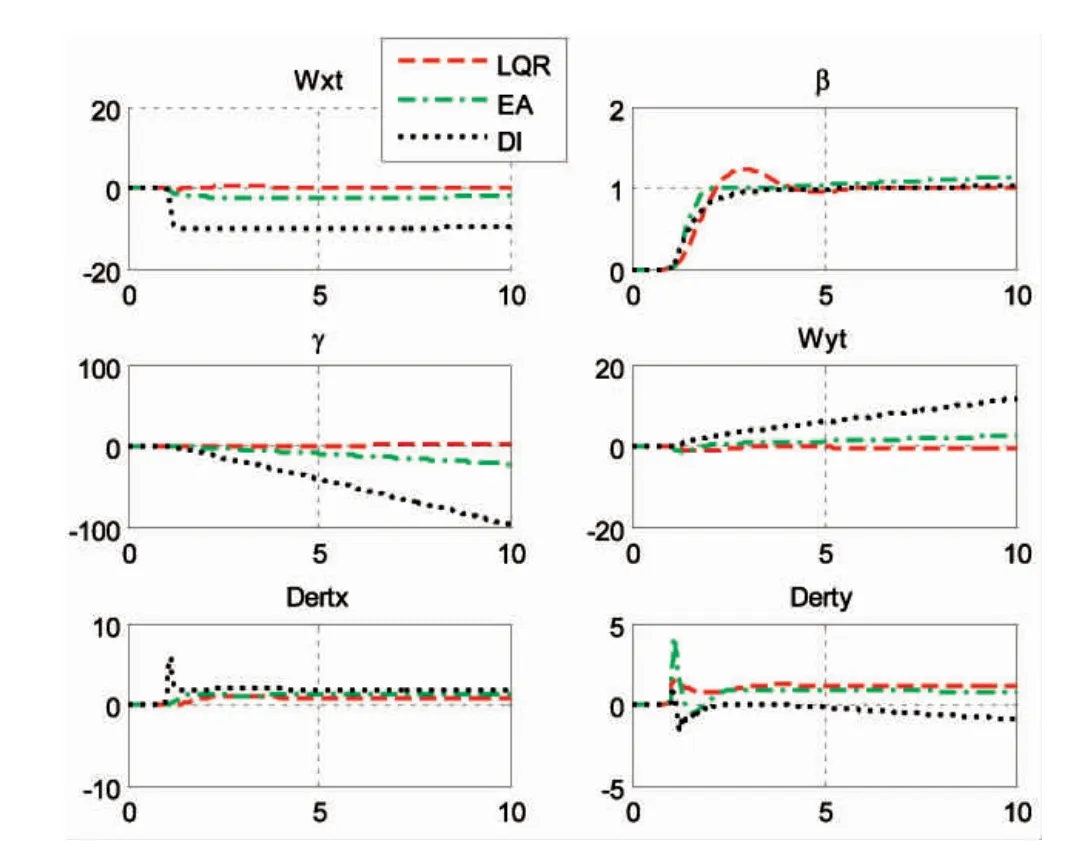
图3 航向仿真结果对比

由上述对比结果可知，当给定10°/s滚转角速率指令时，最优控制方法和动态逆方法的响应速度较特征结构配置的快，但最优控制方法存在超调，而另两种方法均能平滑跟踪指令，三者的稳态误差均几乎为零，特征结构配置方法的横航向解耦效果最优；当给定1°侧滑角指令时，三种方法的响应速度相当，最优控制方法存在超调，动态逆方法给定侧滑角同时产生的滚转角速率较大，解耦效果较前两者差。

设置20%的飞机模型扰动，给出10°/s的滚转角速率指令和1°的侧滑角指令，三种方法仿真结果如图4、图5所示。

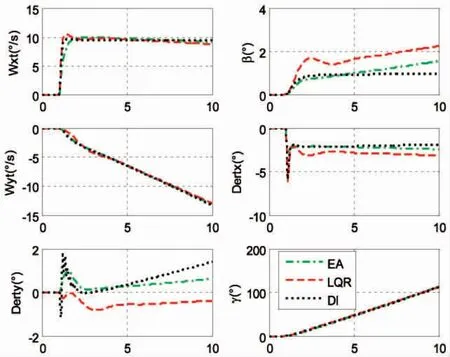
图4 横向仿真结果对比（带扰动）

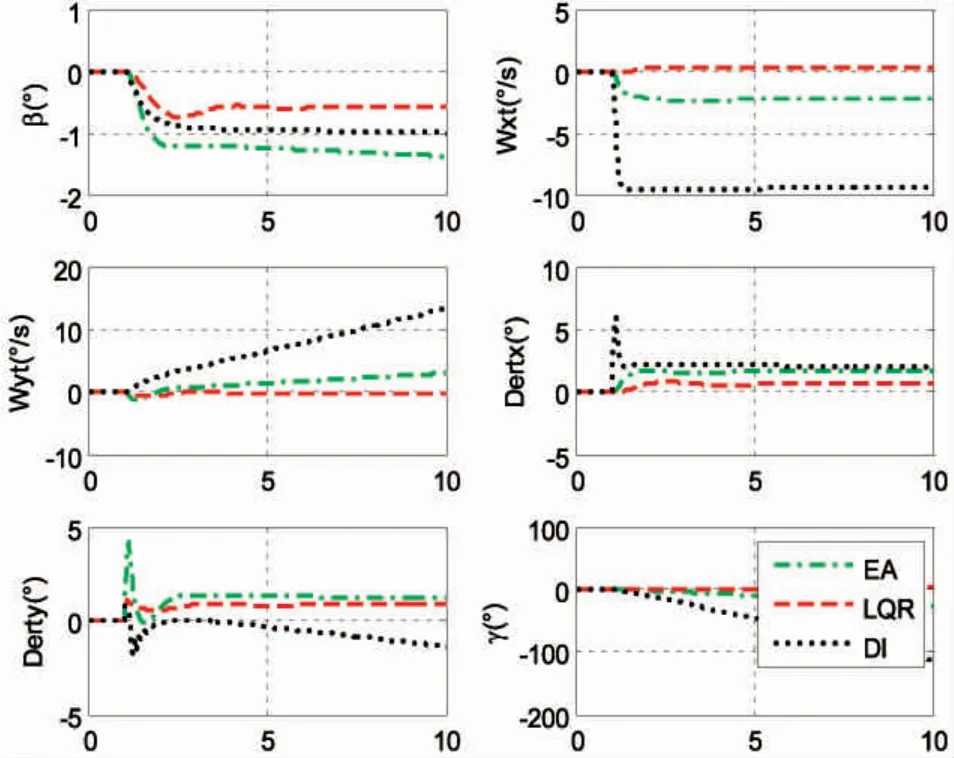
图5 航向仿真结果对比（带扰动）

扰动时，给定10°/s滚转角速率指令时，三种方法都能很好地跟踪指令，最优控制方法略微超调，三者的稳态误差均几乎为零；给定1°侧滑指令时，特征结构配置方法和最优控制方法的侧滑角存在稳态误差。由此可知，三种方法的抗扰动能力相当。

3 结语

本文研究基于现代控制理论方法的飞机横航向控制律设计，其中运用具有工程意义的线性二次型最优控制方法、特征结构配置方法和动态逆方法，以某型教练机5km、0.3M状态点为例，进行横航向控制律设计，搭建Simulink模型，仿真分析并验证。通过仿真结果可知，线性二次型最优控制方法，响应速度快，但存在一定的超调；特征结构配置方法能够平滑较快地跟踪指令，且稳态误差几乎为零，较好地实现了横航向解耦；动态逆方法能够平滑较快地跟踪指令，且稳态误差几乎为零，其给定横向指令时，能够较好地实现横航向解耦，但当给定航向指令时，横航向解耦效果较差。

综上，线性二次型最优控制方法设计过程最为简单，MATLAB中有函数工具，可直接得到反馈控制律，但其最关键的问题是性能指标中Q和R的选择，Q和R的值并没有理论依据，设计过程中需要不断试凑，观察仿真结果来调节Q和R，直至达到期望的仿真结果。

特征结构配置方法的计算过程比较复杂，尤其还涉及复根，选择不同的特征根和特征向量得到的反馈控制律也不同，后期飞行品质计算结果也会受影响，可根据飞行品质计算结果适当调节特征根，使得其动态特性和品质都符合要求。

状态反馈动态逆方法得到的反馈增益偏大，对飞机稳定性影响较大，后期要根据稳定储备的计算加以修正。

较经典理论而言，基于现代控制理论的全状态反馈方法能够一次性求出反馈系数，后续可根据相关飞行品质计算调整个别参数，缩短了控制律设计的时间，提高了效率。