基于自适应近似模型的GTS模型低风阻尾板优化

胡兴军 刘一尘 李金成 兰巍 张扬辉 王靖宇†

(1．吉林大学 汽车仿真与控制国家重点实验室，吉林 长春 130012；2．吉林大学 汽车工程学院，吉林 长春 130012)

随着能源问题的不断凸显，商用车因其能耗较高、受空气阻力影响大的特点，逐渐成为气动减阻领域的研究热点。Hakansson[1]通过改变重型卡车货箱外形及增加各种气动附加装置，发现合理布置的气动附加装置可以达到与流线型货箱同等的气动减阻效果，而并不压缩货箱容积，从而说明了气动附加装置的重要性。其中，尾板由于形状简单、容易布置，且减阻潜能大而获得了广泛关注。Salati等[2]通过对某汽车列车梯形尾板及圆锥形气动附加装置进行研究和优化，发现当梯形尾板倾角为13°时，汽车列车气动阻力系数随着梯形尾板的板长增加呈现出先增加后降低的趋势；Ellis等[3]通过在尾板中间增加副尾板，使得某汽车列车在0°～5°偏航角的平均气动阻力系数降低最高达26%；Hassaan等[4]基于无车轮GTS模型增加尾板结构，并以尾板长度和倾角作为变量探究最优阻力方案减阻机理，发现尾板越长气动阻力系数越小，倾角为15°时气动阻力系数最小，并指出C柱涡引起的上洗气流变化是控制尾部上洗涡、下洗涡分布的关键因素；国内的胡兴军等[5]通过对比5种不同的尾板方案指出，推迟气流分离的尾板方案相比产生分离涡的尾板方案可以获得更大的气动减阻效果。

另一方面，气动减阻中的试验设计(DOE)和优化也是研究重点。张凯歌[6]通过使用静态SVR(支持向量回归)近似模型，对重型卡车尾板进行优化，取得了气动减阻8.2%的成果；Doyle等[7]应用遗传算法(GA)直接驱动CFD程序，从而实现对二维卡车尾板几何的自动寻优，但其执行的GA算法相当于每次产生300个样本点，对于计算量巨大的三维流场仿真很难应用。总体来讲，先构建静态近似模型，再利用某种寻优算法对近似模型进行寻优获得最优点是优化设计的常见思路。但是，静态近似模型主要依靠较多的样本点以实现全局拟合精度，存在数据集获取时间长、优化效率低、样本量计算困难的问题。因此，部分学者转而研究追求最优点拟合精度的自适应近似模型。Jeyasingham等[8]利用ExaADAPT构建自适应采样法，结合RSM(响应面方法)近似模型对某皮卡车型的30个参数进行了气动减阻优化研究，发现该自适应方法可以加速RSM近似模型的收敛过程，并获得预测精度更高的RSM近似模型；Huang等[9]通过构建自适应SVR近似模型对T型管液压成型加载路径进行优化，自适应SVR近似模型只迭代27次便收敛得到Pareto前沿。由此说明自适应近似模型具有较大的优化效率。

本文使用粒子群算法(PSO)完成最小二乘支持向量回归(LSSVR)模型的调参过程，构建自适应PSO-LSSVR近似模型，并采用全局和局部自适应近似模型的方式进一步提高最优解区域的拟合精度，尽量避免陷入局部最优解，同时基于Branin函数为测试函数进行验证；最后将自适应PSO-LSSVR近似模型用于GTS模型低风阻尾板的优化设计上。

1 自适应PSO-LSSVR近似模型的建立

1.1 LSSVR算法

LSSVR算法是将SVR中求解二次规划的问题转换为求解线性方程组的问题，由此可以显著加快收敛速度[10]，算法过程如下。

对于训练集S=(xi,yi),i=1,2,…,n，其中xi∈Rm，作为训练集的m维输入；yi∈R，作为一维输出。在SVR中，将原样本空间中的非线性函数估计问题转化为高维特征空间的线性函数估计问题的表达式如下：

(1)

式中：w=(w1,w2,…，wn)T,为权值系数向量；φ(x)=(φ1(x),…,φn(x))T，为输入映射函数；b为实常量。利用结构风险最小化原理求解，将问题转换为一个等式约束优化问题：

(2)

s.t.yi=wTφ(xi)+b+ei，i=1,2，…,n。

式中，γ为正则化系数，ei为误差项，可在后式中约去。求解上述优化问题，使用Lagrange等式并根据KKT条件得：

(3)

式中，En为n阶单位矩阵，1n=(1,1,…,1)T，y=(y1,y2,…,yn)T，α=(α1,α2,…,αn)T,αi是拉格朗日乘子，Ω=k(xi,xj),k(xi,xj)=φT(xi)φ(yj)，i、j=1,2,…,n。求解α和b后，LSSVR 算法可以表述为

(4)

为了避免“维数灾难”问题，LSSVR引入了核函数[11]。常用的核函数包括线性核函数、多项式核函数、RBF核函数及Sigmoid核函数等。RBF核函数具有普适性强的特点，可以适用于任意分布的样本集[12]，因此本文构建的LSSVR模型采用RBF核函数。RBF核函数表达式如下：

(5)

式中，σ为核函数的宽度。本文的LSSVR模型使用MATLAB LSSVM Toolbox V1.6构建，在该工具箱中，LSSVR模型的σ2和Γ(惩罚因子)决定拟合和泛化能力。已有的文献采用交叉验证法[12]、网格搜索法[13]、核校准[14]等方法进行调参，本文针对上述两个参数，构建二维坐标(σ2，Γ)，采用PSO进行自适应调参。

1.2 PSO-LSSVR近似模型构建方法

PSO算法是一种全局优化的进化算法[15]，因其具有相对较高的求解效率和较快的收敛速度，被广泛用于模型调参、函数优化等领域。

PSO算法的原理是采用一种仅有速度和位置两个属性的粒子来模拟鸟类觅食的过程，其更新速度和位置的公式如下：

vi+1=ωvi+c1(pbest,i-xi)+c2(gbest,i-xi)

(6)

xi+1=xi+vi+1

(7)

式中：i为迭代次数；vi为粒子第i次迭代的速度向量；xi是粒子第i次迭代的位置向量；pbest,i是粒子历史最优解的位置向量；gbest,i是粒子群当前最优解的位置向量；ω是惯性系数，用于调整全局寻优与局部寻优能力，一般取0至1之间；c1和c2被分别称为每个粒子的个体学习因子和社会学习因子，通常取c1=c2=2。

均方根误差(RMSE)因其量纲与数据集相同，更加便于解释误差，因此本文使用验证集的RMSE作为PSO算法的适应度函数。RMSE的计算表达式如下：

(8)

图1 PSO-LSSVR近似模型构建方法

1.3 自适应PSO-LSSVR近似模型构建方法

在自适应近似模型构建中，未达到收敛标准之前，每次迭代产生的解将会被重新放入数据集中，这些解被称为校正点。校正点的选取对模型拟合效果有很大影响，目前较为常见的思路是响应最优策略[9]，即将每次迭代的最优解作为校正点，但Jones等[16]指出响应最优策略容易使得近似模型陷入局部最优解。

另一方面，在利用PSO算法进行LSSVR模型的调参时，将会根据验证集数据RMSE选择最佳超参数。如果验证集是每次迭代后的数据集最优解时，理论上可以获得在数据集最优解处拟合精度最高的近似模型，从而加快寻优速度；但如果数据集的最优解不是全局最优解，则更容易陷入局部最优。

综上，为尽量避免自适应PSO-LSSVR近似模型陷入局部最优解，本文提出一种自适应近似模型构建方法。借鉴逐步缩减求解域[17]的方法，将近似模型分为全局自适应近似模型和局部自适应近似模型两部分，其中全局自适应近似模型的主要目的是较为精确地获得全局最优解的可能位置和数值，为局部自适应近似模型提供边界条件；局部自适应近似模型利用全局自适应近似模型迭代的所有校正点，在全局最优解可能的位置处构建新的自适应近似模型，从而增加全局最优解附近的拟合精度。这样，由于不直接将全局自适应近似模型的最终迭代解作为全局最优解，也就减小了陷入局部最优解的可能，而构建局部自适应近似模型的样本点主要来自以往的校正点，从而加强了样本点的利用率。

同时，为了增强自适应近似模型在最优点附近的搜索能力，自适应近似模型的验证集将从上次迭代预测的最优解实际值和数据集最优解中随机选择，为了保证收敛结果有意义，同一验证集选择方案必须至少保持两次迭代步。全局和局部校正点的收敛标准如下[18]:

(9)

(10)

1.4 优化问题求解策略

自适应PSO-LSSVR近似模型针对单目标优化问题的求解策略如图2所示。

图2 自适应PSO-LSSVR近似模型构建方法

1.5 自适应PSO-LSSVR近似模型寻优算例

1.5.1 测试函数

为验证自适应PSO-LSSVR近似模型的有效性，使用Branin函数[19]作为单目标优化问题测试函数，并使用自适应PSO-LSSVR近似模型进行全局寻优。

Branin函数表达式如下：

(11)

其中，x1∈[-5,10]，x2∈[0,15]，目标函数为minfBF(x1,x2)。该函数理论最优解约为0.397 887，具有3个最优点。

初始全局数据集选取20组样本点，为兼顾训练和验证效果，初始验证集为数据集中函数值最小的两组样本点。MIGA算法个体数为6 000。

1.5.2 Branin函数寻优过程

对初始数据集构建自适应PSO-LSSVR近似模型。取ε1=5%，ε2=1%，N=20。迭代13次后，全局自适应PSO-LSSVR近似模型收敛，进入局部近似模型阶段，迭代3次后，局部自适应PSO-LSSVR近似模型收敛。

自适应PSO-LSSVR近似模型在Branin函数上的校正点迭代过程如图3所示。

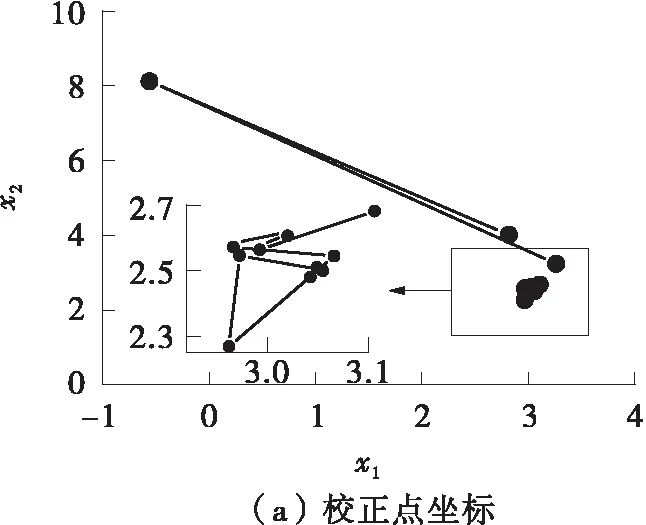
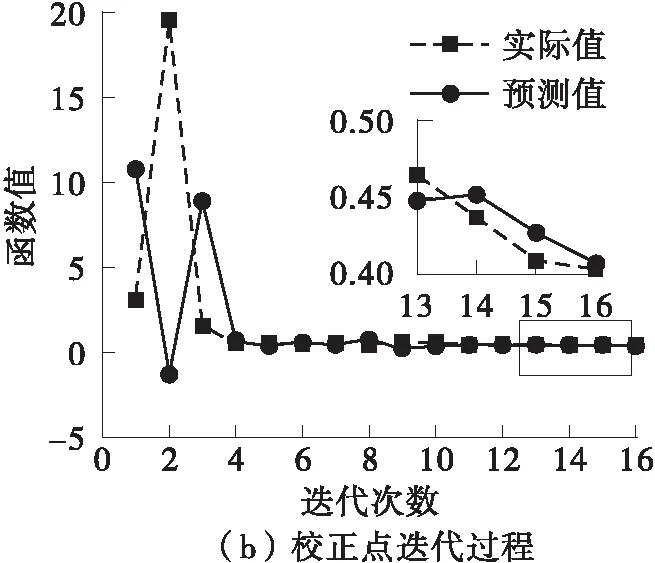
图3 Branin函数自适应寻优过程

1.5.3 与其他常用近似模型寻优的对比

为进一步说明自适应PSO-LSSVR近似模型相对于其他常用近似模型的优势，在Branin函数的基础上，分别使用与自适应PSO-LSSVR近似模型收敛后相等的样本点数量，采用iSight软件构建静态二阶近似模型(2阶RSM)、三阶RSM近似模型(3阶RSM)、静态Kriging近似模型和静态RBF神经网络近似模型(静态RBF NN)，并使用相同参数的MIGA算法进行全局寻优，从而对比得到的最优值及其精度差异。各近似模型在Branin函数上的寻优结果如表1所示。

表1 各近似模型在Branin函数上的寻优结果1)Table 1 Optimization results in Branin function with different approximation models

综上所述，自适应PSO-LSSVR近似模型在同等样本量情况下可以获得更优秀的寻优能力及预测效果，证明其较适合由于样本量获得较为困难而产生的小样本优化问题。本文将应用自适应PSO-LSSVR近似模型对GTS模型低风阻尾板进行优化设计。

2 GTS模型低风阻尾板优化

2.1 GTS模型的计算设置及对标过程

本文采用GTS模型作为车辆研究对象。GTS模型是Sandia National Laboratories Ground Transportation System的基础车辆模型[20]，车辆外形是一种具有货箱的半挂汽车列车，车辆长19.805 m、宽2.590 m、高4.113 m。Gutierrez等[20- 21]对1:8 GTS模型进行了风洞试验，试验结果显示，非侧风工况时，车辆尾部流场呈现出几乎对称分布的流场结构。由于本文仅计算非侧风工况稳态情况，为减少计算量，可认为流场左右对称分布，而只计算半车身。

计算域方案参照SAE J2966-2017标准[22]，为减少计算域宽度对流场的影响，在推荐值基础上增加至15倍半车宽，计算域全长220.0 m(前3倍车长、后7倍车长)、宽19.6 m(15倍半车宽)、高24.0 m(6倍车高)，阻塞比为1.06%。设置3层加密区，按照1:2增长率逐层加密，并对车尾分离区进行了再次加密。多面体网格具有生成与计算效率高、对梯度及局部流动分布预测性好的特点[23]，因此本文使用多面体网格进行划分，网格划分如图4所示。

图4 GTS模型网格划分

数值计算使用STAR-CCM+软件。采用RANS稳态计算方式和SSTk-ω湍流模型进行数值计算,整车边界层厚度为2.16 mm，划分为15层，使得全车绝大部分满足y+≤1的要求，而仅在驾驶室侧部边缘处，由于气流加速使得此处y+～4，为缩小可能带来的计算误差，使用全y+壁面处理功能[1]。残差收敛标准为10-4，气动阻力系数CD收敛后取后300步CD均值作为最终CD计算值。各边界条件如表2所示。

表2 GTS模型仿真边界条件Table 2 Boundary condition of simulation of GTS model

Gutierrez等[20- 21]的试验雷诺数(以车宽作为特征长度)为1.6×106，满足商用车缩比模型风洞试验雷诺数应大于0.5×106的要求[24]，可认为进入雷诺数自准区，气动阻力系数不再改变，这与Storms等[25]的试验结果变化趋势一致,因此可用于气动阻力系数对标过程。网格无关性结果与试验的对标结果如表3所示。

表3 气动阻力系数试验对标结果与网格无关性Table 3 Benchmark of CD and grid independency

1)ΔCD指CD的相对变化量。

由表3可以发现，当半车身体网格数为857万时，气动阻力系数几乎不变，且与试验值的误差小于5%，而进一步增加体网格数使得计算量增长巨大，因此使用857万网格方案进行后续计算。

2.2 GTS模型低风阻尾板的自适应优化过程

对GTS模型增加尾板，并通过自适应PSO-LSSVR近似模型研究最优尾板设计。初始方案尾板形状及几何参数如图5所示。

图5 GTS模型尾板设计变量及初始值

使用相同的仿真策略，得到增加尾板后GTS模型的气动阻力系数为0.312 3，相比无尾板GTS模型下降15.14%。确定上尾板倾角θ1、下尾板倾角θ2、侧尾板倾角θ3和尾板长度L作为设计变量。由于改型前后车辆正投影面积不变，故可将气动阻力系数作为目标函数。

根据后扰流器的设计准则[6]，尾板的长度应满足下式：

(12)

式中，A为商用车的正投影面积，γ′为比例系数，通常取0.28～0.57。计算可得尾板的长度范围为885～1 805 mm。然而在一定情况下，尾板过长不利于侧风稳定，因此选择长度约束条件为500～1 000 mm，尾板各角度的约束条件均为5°～20°。整个优化问题描述可以表达为

minf(θ1,θ2,θ3,L)

(13)

s.t.θ1,θ2,θ3∈[5,20],

L∈[500,1000]。

使用最优拉丁超立方抽样方法对样本空间进行抽样。初始数据集为22组样本点，由于数据集因变量CD极差只有0.06左右，与各自变量极差相差过大，因此对数据集进行归一化以提升LSSVR算法训练效率[26]。归一化算法如下：

(14)

其中，X=(θ1,θ2,θ3,L,CD)。

对初始数据集构建自适应PSO-LSSVR近似模型。为更加贴近实际优化需求，使用反归一化的气动阻力系数控制收敛过程，并取ε1=1%，ε2=0.5%，N=20。初始化近似模型验证集为2组样本点。

迭代6次后全局自适应PSO-LSSVR近似模型收敛，最优结果范围缩小至θ1，norm∈[0.191,0.572]，θ2，norm∈[0.030,0.296]，θ3，norm∈[0.020,0.273]，Lnorm∈[0.939,1.000]，下标norm表示归一化后。迭代3次后局部自适应PSO-LSSVR近似模型收敛。迭代过程如图6所示。

图6 气动阻力系数自适应寻优过程

最优气动阻力系数为CD,norm=-0.018 4,位于θ1,norm=0.523 3、θ2,norm=0.278 4、θ3,norm=0.216 7、Lnorm=0.976 6处。反归一化结果为CD=0.282 5，位于θ1=12.85°、θ2=9.18°、θ3=8.25°、L=988.31 mm处。计算得到该方案的气动阻力系数为0.283 0，自适应近似模型预测误差仅为0.18%，证明了构建的自适应PSO-LSSVR近似模型可以用于GTS模型低气动阻力尾板的优化。

2.3 最优低风阻尾板减阻机理

相对于初始尾板工况，最优尾板工况气动阻力系数下降达9.38%。由图7、图8压力系数分布可知，相比于初始方案，优化后方案在尾板附近流场压力出现回升，由图9可知，优化后车尾表面压力系数明显提高；由图10可以发现，优化后方案的总压为零等值面缩小，说明分离区减小，从而降低了压差阻力。观察图7、图8的速度矢量分布，优化后的尾板使得C柱下洗气流强度减弱，使得上洗气流得到充分发展，上洗涡(B涡)更靠近车尾，下洗涡(A涡)和上洗涡(B涡)呈现出对称分布的特点，驻点上移，使得尾部分离区面积减小，侧板附近的分离涡(C涡)尺度减小。优化后方案的对称面尾流场分布，与Hassaan等[4]对无车轮GTS模型尾板研究中相似板长最低阻力工况的尾流场分布类似。图11是使用λ2涡识别方法得到的尾流分离区涡分布图，可以看出，由于上洗气流强度的减弱，优化后流向涡尺度明显减小，且位置不再紧贴地面。

图7 对称面速度矢量及压力系数分布

图8 Z=2.3 m处的速度矢量及压力系数分布

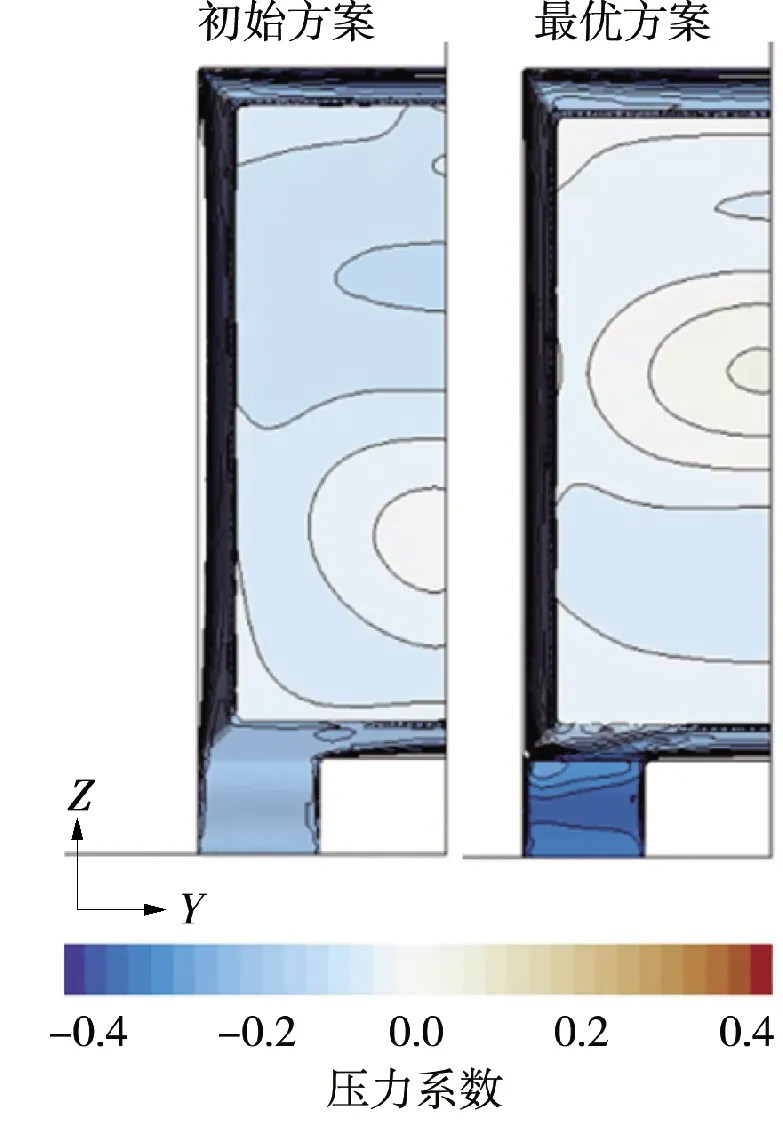
图9 车尾表面压力系数分布

图10 总压为零等值面

3 结论

(1)通过合理选择初始数据集样本量和验证集，基于PSO-LSSVR机器学习算法的自适应近似模型在数据集样本量一定的情况下，于 Branin函数上的寻优能力和拟合精度超过了常用的4种近似模型，说明自适应PSO-LSSVR近似模型优化方法具有较大的快速寻优潜力。

图11 λ2=-5等值面

(2)自适应PSO-LSSVR近似模型可以通过对最优解构建局部近似模型的方法,增强模型在最优解处的拟合精度。

(3)将自适应PSO-LSSVR近似模型优化方法应用在GTS模型低风阻尾板优化上，仅使用31组样本便得出了最优方案，最优方案相比初始方案减阻达9.38%，且局部近似模型拟合误差仅为0.18%。由此说明自适应PSO-LSSVR近似模型优化方法在保证寻优精度的情况下，寻优效率提升明显，适用于单样本点获取耗时较多的小样本单目标优化问题。