车联网环境下基于可变相位的公交优先信号控制方法
2021-07-09宋现敏冷宁姜景玲袁咪莉
宋现敏 冷宁 姜景玲 袁咪莉
(1.吉林大学 交通学院,吉林 长春 130022;2.交通运输部科学研究院,北京 100029)
公交信号优先技术可以减少公交车在交叉口处的延误,提高公交车运行效率,进而增大居民公交出行比例,对于缓解城市交通拥堵具有重要意义。传统的公交优先控制包括被动优先控制、主动优先控制和自适应控制[1- 3]。其中,基于历史交通数据的被动优先控制不能适应交通量波动大、公交车不能按固定时刻和间隔到达等随机情况;而基于固定检测器的主动优先和自适应控制难以评判检测点至停止线间的路段状态,从而无法准确预测公交到达时间[4- 5]。
近年来,车联网技术的兴起为解决上述问题提供了数据支持。在车联网环境下,车辆与控制机之间可实现信息的实时、双向传递,控制系统能够准确获悉交叉口交通状况和公交车运行状态,根据实时数据对其到达时间进行精准预测[6- 7]。因此,许多学者利用车联网环境进行了一系列公交优先信号控制方法的研究。Hu等[8]将公交相位绿灯时间窗口自动滑动的思路应用到公交信号优先策略中,并用微观模拟进行了方法评估;Christofa等[9]基于实时获取的公交乘客占有率,建立了混合整数非线性规划模型,在实现公交车通行权优先分配的同时,社会车辆乘客的延误增加幅度较小;Xu等[10]引入公交优先策略、公交线路等级和过境方式的权重表达式,建立了公交信号优先的优化模型,并以公交车站的人均延误和乘客等待时间为指标评价模型的有效性;Zeng等[11]通过建立随机混合整数模型来确定公交信号优先策略中的最佳绿灯时间;Zamani-pour等[12]提出了一种多模态信号控制统一决策框架,该框架同时考虑了不同出行方式乘客的需求,并用数学优化模型来求解;王永胜等[13]通过插入短相位的方法让公交优先通行,实现了公交优先,但是该方法插入的短相位均为设定好的自然相位。
以往研究多基于固定相序或相位组合进行公交优先控制,缺乏灵活性,而在车联网环境下,可以实时获取交叉口信息,允许动态调整信号相序与相位时长以适应交通需求变化[14],因此,本文采取可变相位的方法进行公交优先信号控制。在动态相位算法的评价指标选取方面,Kari等[15]建立了一个具有有效性度量队列的车辆自适应控制优化器,用车辆排队长度来评价算法的有效性;Wunderlich等[16- 17]以排队长度为公交信号优先选择指标,提出基于最大权重匹配算法的动态信号调度方法,实现了最长排队方向的公交优先调度;Chen等[18]应用车联网技术,实时处理车辆转弯比例和车辆位置信息,以车辆通过流量最大为目标,提出了交叉口动态交通控制框架。
由于车辆排队长度为最易检测且准确性较高的交通参数,因此文献多以排队长度作为相位动态调整指标,忽略了社会车辆与公交车辆的运载差异性,未充分体现公交优先主旨。本文提出了一种基于可变相位的公交信号优先控制策略,建立了确定相位、相序的优先决策框架。在考虑到公交车进入车联网检测范围时的初始状态的基础上,建立了公交车到达时间预测模型,以乘客通过率作为优化目标,设计了公交信号优先算法及求解流程;最后利用VISSIM仿真平台的COM接口与Python搭建了车联网仿真平台,在不同交通条件下对本文提出的公交优先控制方法进行了测试。
1 基于可变相位信号控制的基本思想
1.1 交叉口双环信号控制方法
信号交叉口最常用的信号控制方法是双环信号控制。如图1所示,双环信号控制策略包含两个环:环1(相位1、4、5、8)和环2(相位2、3、6、7)。其信号相位顺序是固定的,在适应动态变化的交通需求方面缺乏灵活性,这会造成绿灯时间的浪费和车辆延误等问题,无法保证交通条件实时变化的情况下车辆顺利通过交叉口。
1.2 交叉口相序和相位组合模型的构建
针对上述问题,本文提出了一种基于车联网环境下信息获取的自适应信号控制策略。假设所有车辆都装置了联网设备,当车辆进入交叉口的通信范围时,车辆可以实时向中央控制器传输交通信息,例如车辆的位置信息、速度信息、载客量信息、车辆编号信息、车辆类型信息等。同时,中央控制器将一个周期的固定相位转换为可变相位,其相位序列与相位时长可进行动态调整。通过收集到的交叉口的实时信息来求解交叉口可变相位控制目标函数,选取使得乘客通过率最大的方案,以最大限度地增加单位绿灯时间内通过的排队人数。
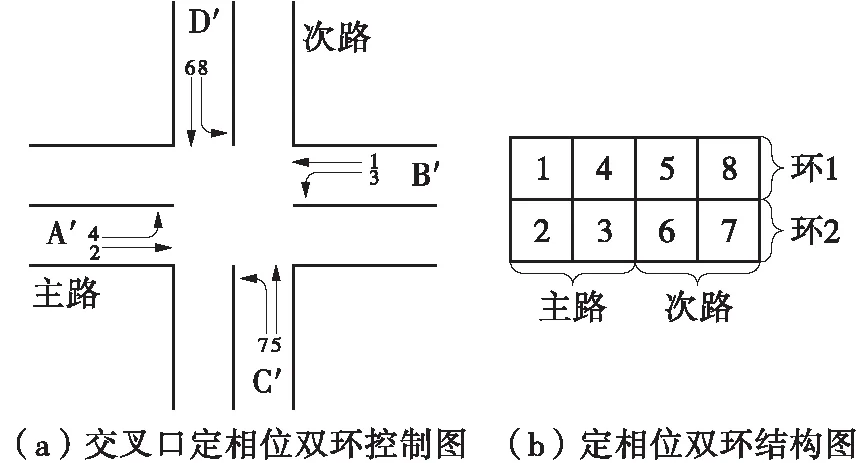
图1 定相位双环控制策略
本文用信号相位矩阵描述信号相位状态,比如具有n个进口道的交叉口,就用n×n矩阵描述其相位状态,则所有相位矩阵的集合组成了该交叉口全部可选相位方案。其中,用“1”表示允许通行,用“0”表示不允许通行。例如用一个4×4矩阵来描述具有4个进口道(A′、B′、C′、D′)的十字交叉口的信号相位状态,如图2所示,在{1,2}相位下,A′进口道通往B′进口道的车辆行驶方向(即由西向东直行)允许通行,由B′进口道通往A′进口道的车辆行驶方向(即由东向西直行)允许通行,以及A′、B′、C′、D′进口道的右转运动允许通行,其他行驶方向则不允许通行。需要注意的是,在相位矩阵中,默认所有进口道的右转方向与其他方向不发生冲突,因而所有右转运动都表示为1。

图2 主路相位矩阵示例
基于上述规则,可以得到主路候选相位矩阵集合A={Aj}(j∈{1,2,3,4}),以及次路候选相位矩阵集合B={Bj}(j∈{1,2,3,4})。其中,A1为东西直行相位,A2为东西左转相位,A3为西进口道直左相位,A4为东进口道直左相位,B1为南北直行相位,B2为南北左转相位,B3为从南进口道直左相位,B4为北进口道直左相位。本文提出的可变相位方法允许在每个阶段中,相位组合与相位序列根据交叉口的实时状况进行动态调整。交通控制器根据实时交通条件从候选相位矩阵选择下一相位矩阵。需要注意的是,在1个周期中,1个方向仅能获取1次绿灯时间,1个相位也只能被选择 1次。图3以主路为例,给出了确定相位次序的逻辑规则,次路的相位次序的确定方法同理。

图3 主路相位次序逻辑规则
图3中:Di为信号阶段,i=1,2,3;A为所有可选相位的集合;Aj(p,q)为含方向p、q的相位Aj,p=1,2,3,4,q=1,2,3,4;“”表示两个集合的差集。
1.3 公交车到达时间预测
当第k辆公交车进入到车联网通信范围,即距离交叉口停止线XA处时,控制系统根据获取的时间、位置、速度等信息,结合实时交通流状况预测第k辆公交车到达交叉口停止线的时间,并根据其进入检测范围时的不同初始状态,将它在检测区间的运行情况分为以下3种:以初始速度Vk直接通过交叉口(情形1)、经历停车排队并跟随车队驶离交叉口(情形2)、减速但不排队后驶离交叉口(情形3)。下面分别对3种运行情况进行分析,以预测第k辆公交车到达时间。
情形1:当j相位p方向的第k辆公交车进入车联网范围(位置XA)时,假设当前相位红灯开始时刻为t0。若公交车无需减速和停车直接通过交叉口,如图4所示,则公交车通过停止线的时间满足:
(1)
(2)
(3)
(4)


图4 情形1下公交到达情况示意图
则第k辆公交车不减速和停车直接通过停止线时应满足如下条件:
(5)
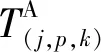
(6)
此时,第k辆公交车通过停止线的时间为
(7)
情形2:当j相位p方向的第k辆公交车进入车联网范围(位置XA)时,设当前相位红灯开始时刻为t0。若公交车需要停车排队,并在绿灯期间跟随车队驶离交叉口,如图5所示,则公交车辆总行程时间包括了公交以自由行驶速度从XA行驶到队列尾端的行程时间、公交排队等待时间和公交重新起动后驶离交叉口的行程时间。

图5 情形2下公交到达示意图
(1)公交行驶到队列尾端的行程时间
如图5所示,公交从XA行驶到排队队列尾端的时间可以通过求解以下方程得到:
(8)
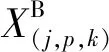
通过求解式(8)中的联立方程组,可得到公交自由行驶到车辆尾端的行程时间和公交行驶至排队队列尾端的停靠位置分别为:
(9)
(10)
(2)公交排队等待时间
当公交车到达队尾后,在队列中排队等待。等待的时间Δt4为起动波传递到公交车的时刻与公交车到达队尾开始排队的时刻之差:

(11)
(3)公交重新起动后驶离交叉口的行程时间
第k辆公交车起动后,继续以排队车辆的消散波速度行驶。公交车从重新起动到驶离交叉口的行程时间为:
(12)
(4)公交到达交叉口停止线时刻的预测
结合式(8)-(12),可推出第k辆公交通过交叉口停止线的时间为:
(13)

(14)
而P点坐标可以由以下联立方程确定:
(15)
从而得P点坐标为
由图6可知,
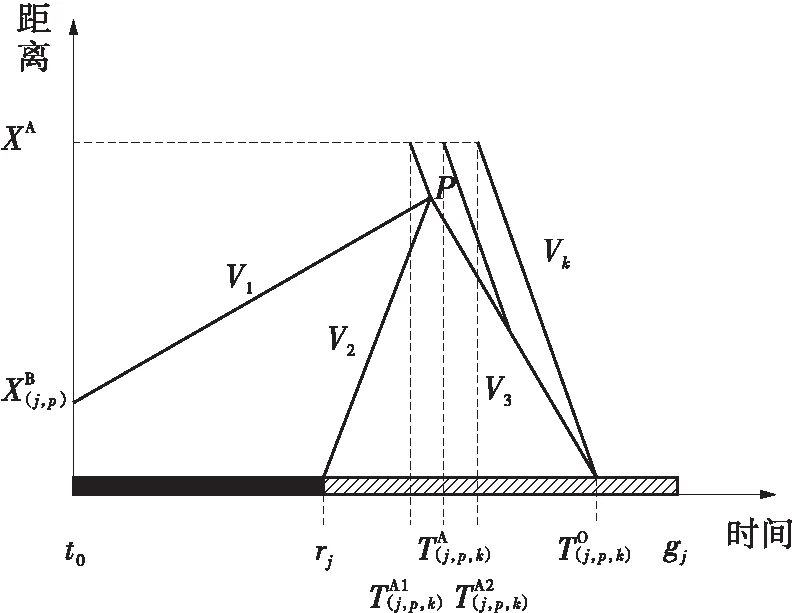
图6 情形3下公交到达示意图
(16)
从而容易算出:
(17)
所以,第k辆公交车经过减速排队不停车时,需满足:
(18)
此时第k辆公交车通过停止线的时间为:
(19)
2 基于可变相位的公交优先信号控制模型
2.1 绿灯时间的确定
(20)
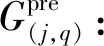
(21)
最终得到j相位所有预测绿灯时间的集合:
(22)
2.2 目标函数
可变相位信号控制算法旨在最大限度地增加单位时间内通过交叉口的排队人数,即使乘客的通过率最大化。对于每一次优化,在通信范围内到达交叉口的排队车辆的乘客都包含在该目标函数中。为了求得最优的配时方案,本文提出了一个以交叉口单位绿灯时间内通过的排队人数最多为目标来求解下一个绿灯相位的公交优先信号控制方法,设定此公交优先信号控制的目标函数为:
(23)

2.3 模型求解流程
可变相位控制算法的思想是在候选相位中选取令乘客通过率最大的方案作为下一相位。若信号组的状态为红灯,可变相位信号控制算法将计算所有8种不冲突的绿灯相位下的目标函数(相位{1,2}、相位{3,4}、相位{1,3}、相位{2,4}、相位{5,6}、相位{7,8}、相位{5,7}、相位{6,8}),以找到在全红状态下最长单位绿灯时间内通过的排队人数的相位,将目标函数最大的相位设置为绿灯相位,并标记选定绿灯相位下的所有车道的排队车辆。
如图7所示,若信号组的状态为绿灯,可变相位信号控制算法将跟踪绿灯相位下被标记的车辆是否通过交叉口。当所有被标记的车辆已通过交叉口停止线或当前绿灯相位时长大于最长绿灯时间时,将此信号机的状态转变为黄灯。当前绿灯相位时长小于最短绿灯时间或被标记的车辆还未通过交叉口时,保持此信号机的状态仍为绿灯。
3 实验
3.1 调查地点的选取
为了评价车联网环境下基于可变相位的公交信号优先算法,本文选取长春市光谷大街与飞跃路交叉口作为实验对象,交叉口平面图如图8所示。光谷大街入口有6条进口道,包含2条左转专用道、3条直行车道与1条提前右转车道;飞跃路入口有5条进口道,包含2条左转专用道、2条直行车道与1条提前右转车道。本文用VISSIM的COM接口,结合Python软件,进行可变相位下公交信号优先仿真试验。本文通过COM接口控制仿真实验,获取地理位置、速度、路线、载客数等车辆信息,动态调整信号相序与相位时长,为公交车辆提供优先。考虑到长春市光谷大街与飞跃路交叉口的各进口道长度、最大排队长度、各相位时长、车辆行驶速度等综合因素,将车联网通信范围设定为500 m。依据现有车联网技术的发展情况,在该范围内既可以保障数据采集的即时性,也可以保证数据传输的质量[19- 20]。其中,设置黄灯时间为3 s,全红时间为1 s,最短绿灯时间为18 s,最长绿灯时间为60 s。社会车辆的乘客数量赋值为1-4的整数,公交车辆的乘客数赋值为1-60的整数。每次实验中基于车辆编号,实验组与对照组的所有车辆的乘客数量赋相同值。

图7 可变相位求解流程
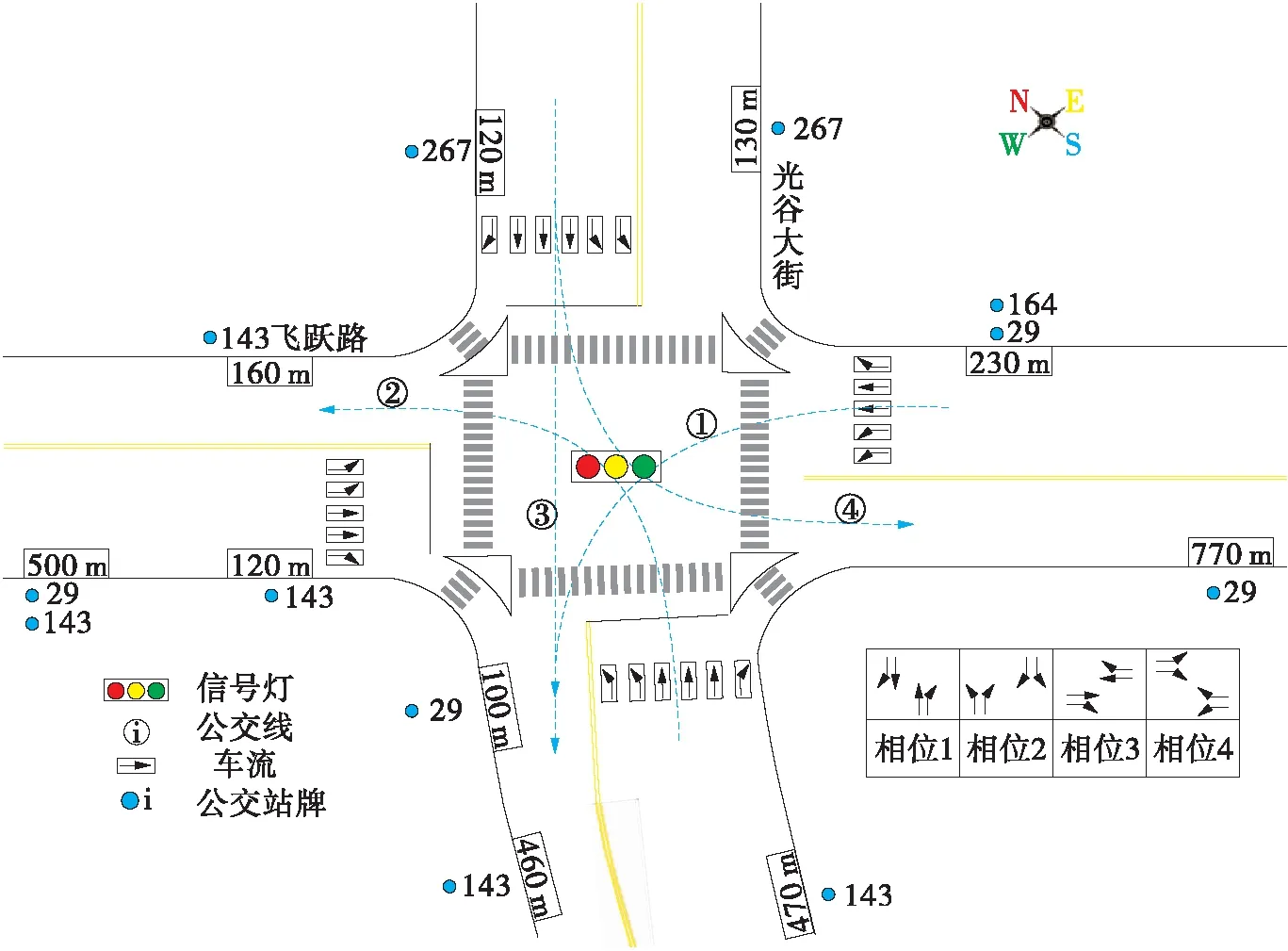
图8 飞跃路与光谷大街交叉口平面图
3.2 不同道路饱和度下的仿真结果及分析
为了验证可变相位下的公交优先信号控制方法在不同道路饱和度下的效益,本节分别在饱和度为0.7、0.8、0.9、1.0、1.1的条件下进行仿真实验。每个饱和度下分别进行10次实验,每次实验的仿真时间为1 h,并将结果取平均值。表1为分别采用无公交优先信号控制方法(方法1)与可变相位公交优先信号控制方法(方法2)下的交叉口人均延误、公交车辆人均延误、社会车辆人均延误。
由表1可知,随着道路饱和度的增加,两种信号控制方法下交叉口人均延误、公交车辆人均延误与社会车辆人均延误均呈现增长的趋势。在各道路饱和度下,对比于无优先控制方法,采用可变相位公交优先信号控制方法后交叉口人均延误明显降低。

表1 不同道路饱和度下可变相位模型仿真结果Table 1 Simulation results of variable phase model under different road saturations
图9给出了不同道路饱和度下人均延误的改善效果。由图9可知,随着道路饱和度的增加,采用可变相位模型的人均延误改善效果(延误减少率,下同)逐渐降低,且在未饱和状态下人均延误改善效果明显优于饱和与过饱和状态。在未饱和的情况下,交叉口人均延误减少比例分别为59.96%、32.01%、25.45%。当交叉口饱和与过饱和时,可变相位模型下交叉口人均延误改善比例小于13%。同样地,随饱和度的增加,公交车辆人均延误改善效果从67.10%减少到了10.27%,社会车辆延误改善比例从52.21%减少到了12.37%。
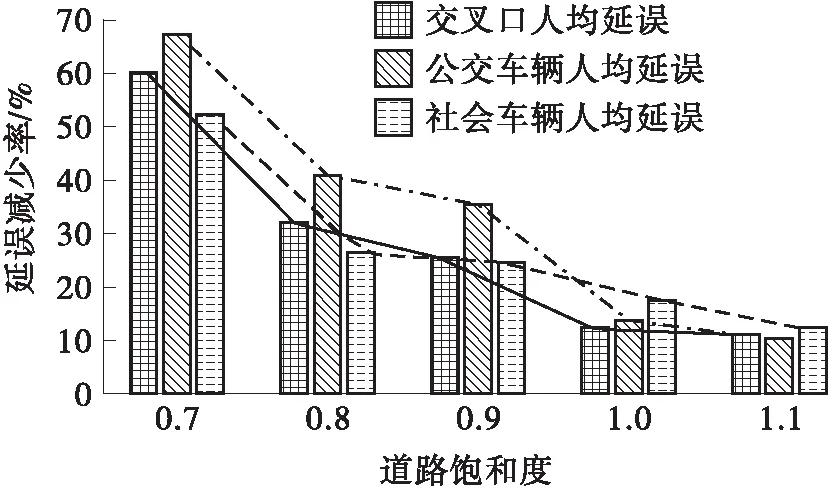
图9 不同道路饱和度下人均延误改善效果
因此,未饱和时,基于可变相位的公交优先信号控制方法对减少公共交通人均延误的效果更为显著;当道路过饱和时,此方法的交叉口人均延误、公交车辆人均延误与社会车辆人均延误的改善效果并不显著。这说明可变相位下的公交优先方法可以在为载客数更多的公交车提供优先权的同时,减少了整个交叉口人均延误,且该方法对于未饱和的道路条件具有更佳的适应性。
3.3 不同公交车比例下的仿真结果及分析
为了验证可变相位下的公交优先信号控制方法在不同公交车比例下的效益,在道路饱和度为0.9的情况下,对公交车比例从2%到20%变化范围内进行仿真实验。在每种公交车比例下进行10次实验,每次实验的仿真时间为1 h,并将结果取平均值,仿真结果如表2所示。
由表2可知,可变相位方法对比于无公交优先方法,整体上减少了交叉口人均延误。采用可变相位方法后,交叉口延误的改善效果比较稳定,不随公交车比例的变化而发生较大波动。
从表2中还可以看出,在公交车比例大于10%时,可变相位方法与无公交优先方法对于公交车人均延误的改善效果都比较稳定,没有太大波动。当公交车比例小于8%时,可变相位方法改善效果愈发明显,逐渐拉大了与无公交优先方法之间的差距,尤其是当公交车比例为2%时,可变相位方法下公交车辆人均延误降低为13.58 s,几乎为无公交优先方法下公交车辆人均延误的一半。因为当公交车比例车降低时,优先请求冲突的可能性随之降低。

表2 不同公交车比例下可变相位模型的仿真结果Table 2 Simulation results of variable phase model under different bus ratios
综上所述,可变相位方法能更有效地满足公交车辆的优先请求,而不用损失其他方向的公交优先请求。
通过表2还可以发现,当公交车比例在10%~20%之间时,社会车辆人均延误改善趋于稳定;而当公交车比例在2%~8%之间时,可变相位方法下的社会车辆人均延误略有增长。这表明在公交车比例较低的情况下,为了满足公交车辆的优先请求,可变相位方法可能会为少数公交车提供优先权而不会明显改善其他社会车辆的人均延误。然而这种情况下,可变相位的延误也小于无公交优先方法,说明并未增加其他社会车辆的负担。
综上所述,可变相位方法在公交车比例较低的情况下,公交优先的效益更显著,而对其他社会车辆的人均延误并无明显改进;在公交车比例较高的情况下,可变相位方法能够同时改善交叉口人均延误、公交车辆人均延误、社会车辆人均延误,但无法保证公交车辆的改善效果大于其他车辆。
3.4 交叉口在不同流量波动状态下的仿真结果及分析
本次仿真实验为比较可变相位方法与定时方法的差异,在VISSIM仿真平台中,将道路流量设置在特定范围内,使其在流量范围内上下波动。本次仿真实验共测试了两种交叉口流量波动状态下,可变相位下的公交优先信号控制方法的效益。每种波动状态下分别进行了10次仿真实验,并将仿真结果取均值。波动性实验的仿真结果如表3、4、5所示,实验将道路波动系数定义为道路饱和度上限与道路饱和度下限的差值。

表3 不同流量波动状态下可变相位模型的交叉口人均延误Table 3 Per person delay of intersection with variable phase model under different flow fluctuation

表4 不同流量波动状态下可变相位模型的公交车辆人均延误Table 4 Per person delay of buses with variable phase model under different flow fluctuation

表5 不同流量波动状态下可变相位模型的社会车辆人均延误Table 5 Per person delay of social vehicles with variable phase model under different flow fluctuation
表3、4、5分别展示了不同道路波动系数下可变相位模型的交叉口人均延误、公交车辆人均延误和社会车辆人均延误变化情况。由表3可知,道路饱和度大于0.8时,无论道路波动系数为0.1还是0.2,延误减少率均小于40%,随着道路饱和度的下降,可变相位优先方法的改善效果越来越明显,延误减少率可以达到60%。由表4可知,当道路饱和度大于0.8时,无论道路波动系数为0.1还是0.2,延误均减少了35%左右,同样随着饱和度的下降,可变相位的优化效果最高可以将人均延误减少70%。由表5可知,当道路饱和度大于0.8时,无论道路波动系数为0.1还是0.2,社会车辆的人均延误改善效果都小于40%,当饱和度小于0.8时,延误改善效果大于40%。以上现象也印证了3.2节提出的可变相位方法更适用于低饱和度道路条件的结论。可变相位模型与定时配时方法相比,其交叉口人均延误、公交车辆人均延误、社会车辆人均延误均大幅度降低;在波动系数为0.1与0.2时,可变相位模型均能够取得较好的效益,且其人均延误减少量无显著差异。
4 结论
本文提出了一种车联网环境下基于可变相位的公交优先信号控制方法,该方法在为公交车提供优先通行权同时,能达到对绿灯时间利用率最大化的目的。该方法的核心是在公交车不同的到达情况下,为下一相位的所有可选方案实时求解出所需绿灯时间,并实施使乘客通过率最大的方案,以达到使交叉口人均延误最小的目的。通过VISSIM仿真平台的COM接口与Python编程软件搭建的车联网仿真平台对该方法进行仿真和评价,结果表明,当道路未饱和时,基于可变相位的公交优先信号控制方法对减少公共交通人均延误的效果更为显著,更适用于未饱和的道路条件。在公交车比例较低的情况下,该方法取得了更佳的效果,对公交优先的效益更显著;而在公交车比例较高的情况下,可变相位方法能够同时改善交叉口人均延误、公交车辆人均延误、社会车辆人均延误,但无法保证公交车辆的改善效果大于其他车辆。
