平流层飞艇升空全过程的热力耦合分析

韩强 唐梓棋 张闰† 刘婷婷 姚小虎

(1.华南理工大学 土木与交通学院，广东 广州 510640；2.中国特种飞行器研究所，湖北 荆门 448000)

平流层飞艇作为一种性能优越的临近空间飞行器，在军用及民用领域都具有极大的应用价值[1- 4]。其一方面可以作为信息平台服役于军事通信、侦查、导航、预警等军用场合[5]；另一方面还能实现民用通讯、电视转播、气象汇报、空中运输及紧急救助等工作[6- 7]。由于其所具有的经济性、空间性、通讯性和前景性，越来越得到各国的重视[8]。

平流层飞艇需依靠气囊提供的浮力实现升空和悬停，同时受到大气、风场等复杂外界环境影响，存在复杂的热力耦合和非线性动力学耦合问题[9]。因此，研究飞艇在升空阶段的热力耦合问题成为了实时控制其运动状态的关键所在[10]。Zhao等[11- 13]介绍了飞艇的动力学模型及关键运动参数的计算方法，通过NPSOL等优化软件，以时间和能源为优化指标对飞艇上升轨迹进行了数值优化；Harada等[14- 15]建立了平流层飞艇的热力学理论模型；姚伟等[16]通过MATLAB的SIMULINK工具箱建立起详细的热力学模型，并进行了初步升空仿真，仿真过程考虑了太阳辐射和对流换热对飞艇上升净浮力和升空过程的影响；Bessert等[17]采用VSAERO与ABAQUS联合分析方法耦合求解飞艇的静气动弹性特征；王晓亮等[18]利用FLUENT与ABAQUS联合结构交错积分耦合法研究了平流层飞艇在突风荷载瞬时响应下的流固耦合特性。整体而言，目前主流文献对平流层飞艇的多物理场耦合研究中，流固耦合方面的报道较多，而具体的热力耦合模型分析以高空驻留阶段的热动力学模型居多，对于升空全过程的热力解耦方案主要停留在理论建模分析阶段，对涉及飞艇变质量升空全过程可视化联合仿真控制方面的研究较为缺乏。

为更全面考虑环境变量对精确模拟升空过程的影响，分析飞艇升空全过程的热力耦合特性，本文以无动力升空平流层飞艇为研究对象，在MATLAB软件中详细建立了包括风场模型和大气模型的动力学和热力学的耦合模型，将多物理场耦合非线性问题进行时域离散化迭代解耦，联合多体动力学软件ADAMS进行飞艇刚体建模及仿真分析，为平流层飞艇变质量升空过程建立了全新的可视化联合仿真方案，并对某型号平流层飞艇升空全过程的热力耦合问题利用该方案进行详细分析。

1 飞艇升空的数学模型

1.1 飞艇的动力学模型

本文对平流层飞艇模型所定义的坐标系如图1所示，其中惯性坐标系记为xyz，其原点为地面起飞点[19]。艇体坐标系记为xbybzb，(xG,yG,zG)为艇体坐标系下飞艇的重心坐标,u、v、w分别表示艇体坐标系下沿xb、yb、zb轴方向的速度，p、q、r分别表示艇体坐标系下绕xb、yb、zb轴转动的角速度分量[20]。对动力学模型做以下假设：①飞艇视为刚体结构，忽略其弹性效应，上升过程中飞艇气囊总体积恒定；②飞艇上升过程中体心与浮心位置一致；③由于飞艇沿艇体坐标系xbObzb的纵向面对称设计，因重力矩的自平衡作用导致飞艇绕艇体轴的转角很小，认为重心、浮心均位于纵向对称面内；④忽略蒙皮磨损、氦气泄露等特殊情况引起的质量变化；⑤假定每个气囊内部气体温度均匀分布(包括主气囊和副气囊)。

图1 平流层飞艇的坐标系示意图

根据平流层飞艇的质点动量定理和动量矩定理，建立6自由度方程：

轴向力(Fx)方程、侧向力(Fy)方程、垂向力(Fz)方程(对应于艇体坐标系xb、yb、zb轴)分别为

(1)

同理，滚转力矩(Mx)方程、俯仰力矩(My)方程、偏航力矩(Mz)方程(对应于艇体坐标系xb、yb、zb轴)分别为

(2)

式中：m表示飞艇的总体质量；(Fx,Fy,Fz)、(Mx,My,Mz)分别表示作用于飞艇体心点、在3个艇体坐标轴的合力分量及绕3个艇体坐标轴转动的合力矩分量，下标l表示流体惯性力(附加质量力)，下标at表示空气动力(受大气风场影响)，下标G表示重力，下标B表示浮力；(Ix,Iy,Iz)、(Ixy,Ixz,Iyz)分别表示绕艇体坐标系的惯性矩和惯性积。

飞艇的附加质量是飞艇升空过程中受到周围流体所引起的惯性力，其主要与飞艇速度和尺寸效应有关。常见的附加质量计算[21- 22]均是基于Lamb所提的标准公式[23]，经几何转化，得到艇体坐标系下的附加质量矩阵为

(3)

式中，mi(i=1,2,…,6)为飞艇在理想流体中以单位(角)加速度运动时所受的流体惯性力矩阵中的对角线元素。

飞艇所受空气动力主要与飞艇外形、速度和大气环境有关，风荷载的影响主要体现在风速对空气动力的影响上，因此，可利用风洞试验拟合得到的空气动力系数Ci(i=Fx、Fy、Fz、Mx、My、Mz)，根据下式计算在艇体坐标系下的空气动力各分量[24]：

(4)

基于惯性坐标系与艇体坐标系之间的几何转化关系[25]，由运动学推导，得到艇体在惯性坐标系下姿态角变化率及位移变化率的表达式：

(5)

1.2 飞艇热力学模型

平流层飞艇在升空过程中的热交换示意如图2所示，根据式(6)的能量守恒方程，可建立平流层飞艇内部各子系统的能量方程[26]：

(6)

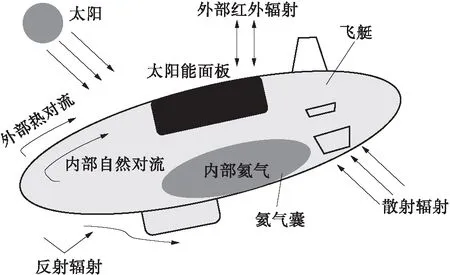
图2 平流层飞艇的热力学模型

(1)气囊子系统

在时间微元dt足够小的情况下，飞艇上升加速度不会太大，囊内无气流能量的变化。假设囊内气体质量在dt内保持不变，可根据下式求得每个气囊内的气体能量变化值：

dEsys,i=dQi+dWi=micp,idTi

(7)

式中，mi为某单个气囊i内部气体总质量，cp,i为定压比热容，dQi为单个气囊通过边界吸收的热量，dWi为外界对单个气囊所做的功。根据式(7)可求得单位时间内的温度变化值dTi，对时间微元内温度变化量积分可得到任意时刻的温度值；同时可根据式(7)求得任一时刻的气囊内部气体温度，然后利用理想气体状态方程求得任一时刻的压强值，即可求得气囊内外的压强差。

(2)蒙皮子系统

由于艇体的蒙皮分布较广，不同位置热交换条件均不同，因此蒙皮的温度计算按多区域分别计算。考虑到蒙皮系统的能量变化以热交换为主，因此式(6)可简化为下式：

dEsys,j=dQj=mjcjdTj

(8)

式中，mj为所划分区域j的蒙皮面质量，cj为对应区域j的蒙皮比热容。使用式(8)求得每一区域蒙皮的均布温度Tj。

1.3 热力解耦

在动力学方程(式(1)、(2))中，重力、浮力、空气动力均与气体的密度有关，根据理想气体状态方程：

PV=nRT=NKT

(9)

或

PM=ρRT

(10)

式中：P为理想气体的压强；V为理想气体的体积；n为气体物质的量；R为理想气体常数；T为理想气体的热力学温度；K为波尔兹曼常数；N表示气体粒子数；M为理想气体的摩尔质量；ρ为气体密度。由式(10)可知密度是受温度影响的量，因此，重力、浮力、空气动力均为关于温度的函数：

(11)

由式(11)可知，在任一时刻，动力学模型与热力学模型中各参数均与温度相互耦合，因此需要将方程进行时域离散，对各时间微元dt进行解耦分析。由排气控制方程，根据tk时刻囊内气体密度ρ1、囊体内外压差ΔP、温度量Tair推导出飞艇在tk+1时刻的总质量，艇体质量变化方程如下:

(12)

式中：nr为排气阀个数；s为单个排气阀的面积；C为排气常数；Pm为气囊内外压差的设计最小值；V1为单个气囊的体积；Rair为空气的常数系数。

根据动力学模型，采用时域离散对全过程进行逐步求解。将升空全过程时间域[0,t]均分为k段，不失一般性，对其中[tk,tk+1]时间段，可得到速度场方程增量形式如下：

(13)

其中dt=tk+1-tk。同理，位移场方程为

(14)

同样可根据tk时刻的温度场求解tk+1时刻的温度场:

(15)

式中：Tfilm、THe、Tair分别表示飞艇蒙皮(蒙皮划分为多区域，此处为某区域的蒙皮)、主气囊氦气及副气囊气体的温度值；mfilm、mHe、mair分别表示飞艇某区域蒙皮、氦气、副气囊气体的质量；cfilm、cHe、cair分别表示飞艇某区域蒙皮、氦气、副气囊气体的比热容。

根据式(12)-(15)，可由tk时刻的物理量推导出tk+1时刻的温度与力场。但由于tk+1力场是根据tk时刻的各物理量推导得来，然后根据比热容公式利用tk+1的各力场求得tk+1时刻的温度，因此tk+1时刻的温度与各力场之间存在着误差而无法自洽。因此在上述时域离散方法基础上，文中通过设定求解控制误差进行迭代收敛计算，标准为最后一次迭代与上一次迭代的温度差值不大于0.000 1 K，流程图如图3所示。

图3 飞艇热力解耦流程示意图

2 数值计算

2.1 模型构造及初始参数

基于前述模型搭建方法及解耦方案，本节对某型号在研平流层飞艇进行示例仿真，艇身主要由主气囊、前副气囊、后副气囊3部分构成，初始参数如表1所示。

表1 飞艇初始状态主要设计参数Table 1 Main design parameters for the initial state of airship

飞艇的示例仿真选定放飞时刻的气象条件为晴天，忽略大气湿度对升空的影响。根据选定的放飞经度和纬度及具体放飞时间点(北京时间08：00)确定放飞温度为298 K。为了说明联合仿真方法的普适性，选定不同的气囊内外压差设计最小值和不同地面放飞温度进行升空仿真研究。根据统计的平均风场数据，平均风速模型按表2线性插值选取。

表2 平均风速的插值表Table 2 Interpolation table of mean wind-speed

主气囊内填充氦气、副气囊内填充空气与氦气的混合气体，主气囊不排气且可自由膨胀，副气囊通过排气阀门开闭个数控制排气量的多少，从而控制飞艇升空过程的飞行速度、姿态及内外压差。

2.2 联合仿真过程

联合仿真过程主要步骤如下：

步骤1根据运动学方程和能量守恒定律，在MATLAB中建立飞艇的热力学耦合模型并进行热力解耦，得到飞艇升空段的质量变化曲线和作用于艇体坐标轴的3个分力以及绕飞艇3个坐标轴转动的分力矩时程曲线；

步骤2在CATIA软件中建立飞艇几何模型，并将其保存为通用格式文件，用ADAMS导入通用格式文件组装成飞艇的6自由度总体模型，并定义材料属性及建立参考坐标系和特征点；

步骤3结合步骤1求解得到的升空过程变质量时程曲线，开发可模拟飞艇在升空过程中的实时变质量升空的ADAMS子程序，通过子程序调用步骤1中解耦所得的飞艇变质量数据来实现飞艇变质量升空仿真；

步骤4由于本文研究暂不关注飞艇薄膜应力分布，因此基于刚体结构及对称简化假设，考虑计算效率，根据力的平移定理，将MATLAB中解耦后得到的所有力场都转化施加至ADAMS的飞艇模型体心点上，故分析结果具有纵向对称性，无需额外施加对称约束，模型荷载示意如图4所示。图中使用脚本仿真类型，分析平流层飞艇整体升空段的动态响应效果。

图4 模型荷载示意图

2.3 ADAMS子程序的开发

多体动力学软件ADAMS在求解多刚体问题时使用拉格朗日坐标系，ADAMS/View不能提供改变质量的函数，无法模拟在过程中刚体质量的改变，与真实的平流层飞艇升空过程质量不断减少不相符，本方法利用通用程序设计语言——C语言开发能在Adams/Solver中，以交互式或批处理形式计算的CONSUB子程序[27]，以实现升空过程飞艇模型质量变化。该CONSUB子程序开发及调用的主要流程如图5所示，它首先利用C语言编写变质量子程序代码块；之后使用Visual studio本地命令提示符工具进入ADAMS环境中进行编译，编译过程使用Intel visual Fortran的多个静态链接库lib文件；最后在ADAMS中的平流层飞艇模型上施加6自由度荷载，同时定义脚本仿真类型，在脚本中指定唤起子程序的命令，并对求解器指定已编译好的子程序文件。

图5 子程序开发及调用流程图

3 热力耦合结果分析

为研究平流层飞艇在调用变质量子程序下的动态响应，选取沿惯性坐标系z轴和绕y轴旋转两个主要自由度的运动进行详细分析，具体对应于飞艇在不同的气囊内外压差的设计最小值下的运动学响应量；同时分析了不同地面放飞温度下主气囊内氦气温度的变化规律。

3.1 运动轨迹

由式(11)可知，飞艇的排气上升过程受气囊内外压差的设计最小值Pm的控制。由于蒙皮材料的材料性能有限，Pm不宜过大也不宜过小，因此分别选取200、300、400 Pa的设计值进行仿真分析，研究平流层飞艇在气囊内外压差的不同设计最小值Pm情况下，变质量上升过程(0～14 000 s)中的速度与高度及俯仰角与高度的变化曲线。

由图6可见，飞艇在前期为加速上升阶段，副气囊排出气体，主气囊中氦气膨胀，对外做功，温度下降。随着速度的增大，气囊排气量减少，气囊内外密度差减小，初始阶段净浮力损失较多，导致飞艇上升加速度在之后一段时间内出现负值，上升速度达至峰值后开始减小，随后又开始上升到达一个较为稳定的速度平台。当飞艇高度达11.0 km时开始进入平流层，气囊内氦气可能出现“超冷”现象而导致飞艇上升速度迅速降低。然而随着飞艇的不断上升，太阳辐射较为显著，气囊内温度缓慢回升，因此可看到飞艇速度迅速降低后逐渐缓慢减小直至接近零；同时可观察到囊内外最小压差不同设计值虽对速度有所影响，但影响不显著，速度的发展趋势仍较为一致。

图6 不同Pm下的高度-速度变化曲线

平流层飞艇与高空热气球同为临界空间飞行器，且两者的无动力升空运动具有一定的相似规律性[28]，因此可参考高空热气球的放飞试验数据来进行飞艇的升空设计和策略控制。图7中将仿真结果与GPS测试的高空气球速度曲线[29]对比可发现，平流层飞行器在无动力升空过程中均表现为前期速度迅速增大到达峰值，然后又快速下降到一个速度平台，进入平流层后速度又再次减小，最后将不断波动或者缓慢减小为零，在最大升空高度处以接近于零的小速度量上下浮动。以上速度变化规律与临近空间飞行器试验所得的合理上升速度区间相一致[30]，从而进一步验证了该联合仿真分析方法的合理性。

3.2 运动姿态

根据该型号平流层飞艇设计要求，飞艇升空过程中俯仰角变化不可过大，需保证在重力矩的自动调节作用下，飞艇维持在一定俯仰角范围内而稳定平直上升。研究气囊内外不同压差设计最小值下俯仰角的变化，如图8所示。飞艇升空过程的俯仰角度主要在0°～2.5°的小范围内不断震荡，这是由于升空过程中，当飞艇俯仰角过大时会受到回复力矩的作用，从而使其回复到一定稳定范围内。同时由于平流层飞艇俯仰角度主要受重心与体心间距及排气控制的影响，而本示例的控制方案设计中重心与体心间距较小，前后气囊的排气量较一致，因此对比不同组的俯仰角可知，气囊内外压差设计最小值的变化对俯仰角的影响可忽略不计，可不作为飞艇姿态控制的关键因素考虑。在考虑风场、重力、浮力等多物理场影响条件下，图9给出了当预设气囊内外压差设计最小值为300 Pa时，通过联合仿真获得的典型时刻飞艇的可视化姿态。

图7 不同Pm下的速度-时程曲线

图8 平流层飞艇俯仰角-高度曲线

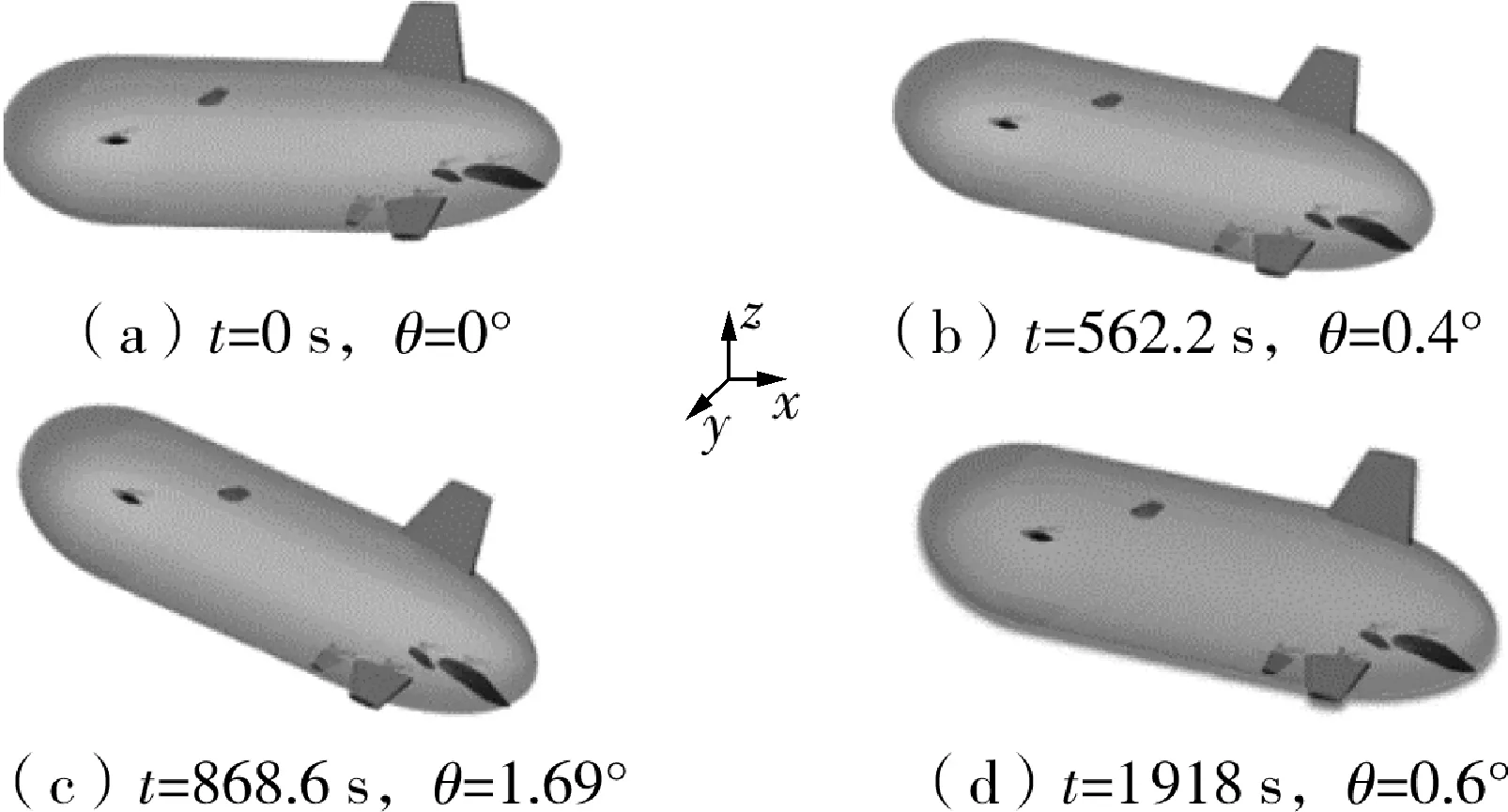
图9 平流层飞艇典型姿态示意图

3.3 主气囊氦气的温度分析

利用联合仿真方法研究飞艇上升段的主气囊在不同地面放飞温度下的氦气温度变化情况。仿真结果与高空热气球的测试数据如图10所示，在对流层底层(上升前期)，飞艇上升速度较快，副气囊排气明显，主气囊温度下降较快，主要受对流换热及主气囊膨胀做功控制；在对流层中顶层(上升中期)，飞艇速度缓慢，气囊排气量减少，囊内气体温度下降变缓；进入平流层后(上升后期)，太阳辐射明显，蒙皮吸热逐渐升温，与主气囊内氦气热交换显著，“超冷”现象逐渐消失，更有利于飞艇的进一步升空。

图10 不同放飞温度下主气囊氦气高度-温度曲线

由图10可知，地面放飞温度越高，在对流层的同一升空高度气囊内气体的温度越高，随着高度的增加，温度的变化具有一致的降低趋势。由于平流层飞艇与高空热气球在无动力升空中的热交换条件几乎一致，因此仿真数据与高空热气球试验[31]测得的氦气温度具有较大的拟合性，均表现出与ISA大气温度模型相一致的变化规律：0～20 km区间内，在对流层中温度随高度上升而降低，而进入平流层后温度又缓慢回升至216 K左右。这一温度变化规律与临近空间飞行器的真实放飞试验结果相符合[32]，从而验证了仿真结果的可靠性。

4 结论

本文通过所提出的新型热力耦合分析方法，对某型号平流层飞艇进行基于MATLAB和ADAMS的联合仿真分析，并首次结合C语言开发了ADAMS环境下变质量子程序，实现对飞艇升空全过程的可视化模拟，主要得出以下结论：

(1)针对飞艇的热力学模型与动力学模型复杂耦合问题，文中在综合考虑了风场模型、大气模型等详细模型基础上，提出了一种有效的时域离散迭代解耦方法，能快速、准确求解出平流层飞艇的升空过程中所受的荷载和温度场。

(2)与传统平流层飞艇分析方法对比，文中基于AdamsSolver求解器开发了变质量仿真分析的CONSUB子程序，有效解决了现有的有限元分析方法无法实现平流层飞艇全过程变质量升空的仿真技术问题。

(3)在考虑多物理场耦合作用下，提供了一种基于MATLAB与ADAMS的平流层飞艇变质量联合升空控制的高效仿真控制方法，经仿真分析获得飞艇在任意升空时刻的运动状态和边界条件，为进一步研究飞艇的刚柔耦合、流固耦合问题提供参考。

(4)仿真结果与试验结果对比表明，即使飞艇的地面放飞温度不一致，但其升空过程中均表现出较一致的温度场变化趋势：飞艇进入平流层前，气囊内气体温度由于“超冷”现象的出现达到温度最低点，进入平流层后太阳辐射加强导致囊内气体温度逐渐回升；同时飞艇速度在进入平流层后开始缓慢降低直至接近零，最后飞艇将在悬停高度范围以较小的速度上下浮动。该结论对飞艇的温度及速度控制设计有重要的指导意义。

(5)平流层飞艇在升空过程中由于受到重力、浮力、空气动力共同作用，一旦上升俯仰角过大，将受到回复力矩的负反馈作用，导致飞艇的升空全过程俯仰角在0°～2.5°之间平稳波动；同时可发现气囊内外最小压差设计值对速度的实时变化控制不明显。以上结论可为飞艇姿态分析及气囊内外压差和排气控制的有效设计提供参考。