针对二维双曲守恒律方程求解方法的研究
2021-07-08吕梦迪
吕梦迪
(陕西国际商贸学院,陕西 咸阳 712046)
1 引言
计算流体力学是基于数值方法对满足定解条件的流体力学方程进行的离散化处理,借助于电子计算机求得相应方程的数值解,并对数值解进行进一步的分析和处理,通过数值模拟的过程得到流体的运动规律,进而解决流体运动中遇到的实际问题。
双曲守恒律方程的数值解是以计算机为工具对双曲守恒律方程进行数值求解的一种方法。早在二十世纪三十年代,国外数学家就开始了偏微分方程的理论研究,Courant,Friedrichs和Lewy等人对双曲守恒律方程的解的存在性和惟一性进行了最早的研究,并给出了著名的稳定性判别条件--CFL条件,为差分法的进一步发展打下了坚实的基础。Lax在1954年提出了弱解的概念,且在弱解意义下允许间断解的存在,但是弱解并不是惟一确定的,因此很多数值方法无法保证其具有物理意义。满足“粘性消失”的Cauchy问题的解在任何时刻是唯一的具有物理意义的解,这种解被称为“熵解”,Lax于1973年从热力学第二定律出发,证明了熵稳定条件可由一个单元熵不等式来表示。满足熵条件的守恒型差分格式被称为熵稳定格式,不满足熵稳定条件的解被称为非物理解,其数值模拟结果表现出常见的“膨胀激波”、“奇偶失联”和“红斑”等非物理现象。
2 国内外研究现状及发展趋势
为了达到熵稳定条件,同时避免非物理现象的产生,人们常用的做法是通过引入额外的耗散机制来抑制熵的变化。理论研究在格式的相容性、收敛性和稳定性方面取得了卓有成效的发展,Lax由等价性定理建立了稳定性和收敛性之间的关系,出现了Richtmyer和Lax的Fourier分析法。随着计算机科学技术的发展和应用,出现了各种数值方法,如Tadmor[1]于1987年提出了二阶的熵守恒格式,并且证明了一个三点格式是熵稳定的,只需含有比熵守恒格式更多的粘性,熵稳定这一概念为获得具有物理意义且数值上稳定的解提供了思路。2006年,Roe[2]在2006年将自己提出的数值粘性项添加在熵守恒格式上,以此得到了ERoe格式,该熵稳定格式能够有效地避免解在间断区域的伪振荡现象,但是该格式是一阶精度的。2009年,Roe和Ismail[3]在2009年深入研究了解在跨过激波时熵增在数量上是激波强度的立方阶量级,即熵相容格式,该格式容易达到熵稳定条件且数值结果更符合真实的物理现象。封建湖、郑素佩、程晓晗、任炯、刘友琼[4-7]等人构造了高分辨率熵相容格式并成功运用于双曲守恒律方程的求解中。
由于熵稳定格式的解在间断处会出现过度抹平的现象,利用传统的高精度格式求解方程在间断处会产生伪振荡现象,因此,如何构造高精度的数值计算方法,使之能够精确地捕捉到激波和这些间断,并且避免伪振荡地产生,一直以来都是科研工作者致力于研究的焦点。针对以上问题,以Harten为首的科研者提出了高分辨率TVD(Total Variation Diminishing)格式[8],从此打开了高精度格式的构造之路。随之又出现了TVB(Total Variation Bounded)格式,ENO(Essentially Non-oscillatory)格式[9]、WENO(Weighted ENO)格式[10]和CWENO(Central WENO) 格式[11]等。郑素佩、吕梦迪[12-15]等人构造了三阶、四阶、五阶的紧凑CWENO格式,并成功应用于双曲守恒律方程的求解中。
3 二维双曲守恒律方程的数值求解方法
双曲守恒律方程是计算流体力学中一类反映物理现象和规律的重要方程。通常情况下,二维守恒律方程具有如下形式:

即方程(1)也可以写成:

此方程(1)被称为二维双曲型守恒律方程。
3.1 熵守恒格式
给定一组熵对(P,Q,R),对于 ∀u∈Rn,均有:

该格式被称为具有二阶精度的熵守恒格式。
3.2 熵稳定格式
熵守恒格式能够保持总熵不变。但在激波等间断处会产生振荡,根据比较原则,若在熵守恒格式上添加合适的耗散项,使得总熵有所耗散,由此避免伪振荡地产生,则该格式被称为熵稳定格式。Roe 用熵守恒格式代替Roe 通量函数中的算术平均数,从而得到新的数值通量函数为:
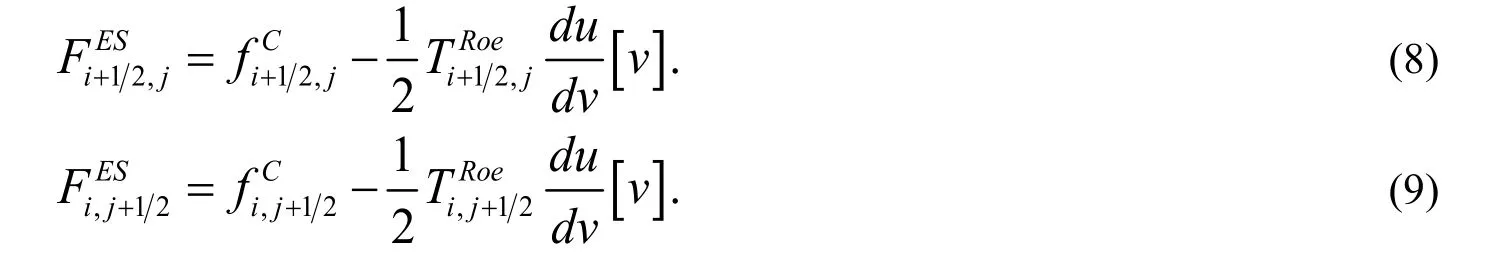
其中以x方向为例,可知:


该格式被称为熵稳定格式。
3.3 熵相容格式
Ismail 发现熵稳定格式中的粘性项的解在跨过激波时达不到应有的熵增,若要达到应有熵增,就需要在熵稳定格式的基础上添加额外的耗散项来满足熵的色散,其数值通量函数为:
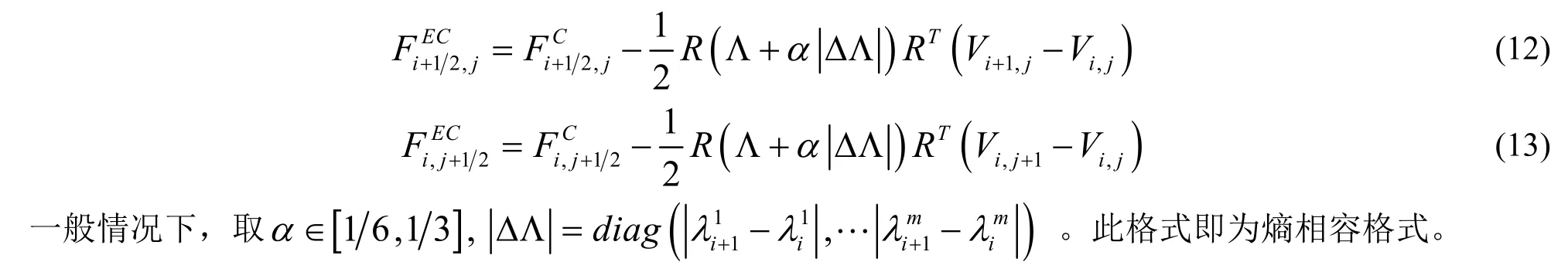
3.4 高分辨率熵稳定格式
分别给(12)、(13)式添加适当的限制器,得到高分辨率双曲守恒律方程的熵稳定格式的数值通量为:

4 结语
本文针对二维双曲守恒律方程的求解问题,主要介绍了熵守恒、熵稳定、熵相容格式,并分析了提高格式精度的高分辨率熵稳定格式,这些方法易于计算机编程实现以及向高维双曲守恒律方程的推广,即对双曲守恒律方程的求解问题有重要的研究意义。但对于二维双曲守恒律方程,有一些问题需要我们继续研究。比如如何更好地控制二维问题中常出现的“红斑”现象;如何基于非结构网格构造高分辨率的熵稳定格式;如何提高格式的分辨率以及二维甚至多维熵稳定格式高分辨率理论研究等。
