基于双正交基字典学习的图像去噪方法

刘伟华，刘 聪

(1.湖北科技学院 五官医学院，湖北 咸宁 437100；2.湖北科技学院 学报编辑部，湖北 咸宁 437100)

通过对图像去噪处理，能够将受到噪声污染的图像进行原始图像的恢复，在对图像去噪中产生了诸多的方法，如小波变换、轮廓小波变换等，但这些方法在使用中都存在一定的局限性，每种变换并不能对所有的特征实现有效地表示。为了促进对图像去噪效果的提升，借助超完备的字典当作图像稀疏的表示，实现对图像各种的几何奇异性特征表现，基于贝叶斯的框架，按照以图像块稀疏的表示对全局图像的先验概率相应模型进行建立，从而给出最大化后验概率的模型下图像优化去噪的算法。此方法对正交基特点充分利用，通过SVD的方法实现字典高效学习，从而提升围像去噪的性能。

一、图像去噪方法综合分析

在图像去噪的传统方法中，比较常用经典型去噪的方法有均值的滤波、中值的滤波和维纳线性的滤波等，它们主要是对空域或者频域进行局部地分析，尽管对图像噪声实现了抑制，但也导致图像的细节信息发生损失，造成去噪后的图像变得模糊。其中空域内均值的滤波主要是对全部像素点实施均值的处理，将其像素点当作中心，对小邻域中全部像素点实施加权和平均值，并将其当作中心性像素点完成滤波后的值，此算法十分简单、易懂，且对各种的图像以及各类噪声都能够实现处理，但因为仅表现出一种平滑的过程，若图像特征的本身并不具备很好的平滑性，往往处理的结果就不理想[1]。对于中值滤波和维纳线性的滤波法等来说，此类一般只对图像数据内二阶统计的特性使用，图像内重要的特征往往借助高阶统计的特性进行体现，因此此类方法的图像去噪效果并不是很好。图像内有用的信息部分与噪声在频带上会出现重叠的情况，这也是以有用信息与噪声频率的特性差别为基础的传统法出现缺陷的本质原因[2]。还以一些其他常见去噪法，如小波域法、几何尺度的分析法和主成分的分量法等，在基于字典学习的图像去噪方法研究逐渐研究深入背景下，其在图像的去噪中逐渐得到了广泛应用。

二、字典学习去噪法概述

对于图像噪声来说，它主要由人为的定义高斯、椒盐和均值等噪声通过混合而构成，想要对此类噪声综合去除，人们可以建立两个以上基函数图像信号进行表示，它的结果比用任何单一基函数的效果要好很多。通过超完备冗余的函数库对基函数取代，称作冗余的字典，此字典内的元素称作原子。对原子库选择中，要尽可能好和被逼近图像信号的结构符合，对其构成可以不进行限制，自原子库内寻找具备最佳组合M项的原子进行一个信号的表示，这就被称作信号稀疏的逼近[3]。

随着不断发展，以字典学习为基础的去噪法以及以非局部的自相似性为基础的去噪法逐渐受到了行业内学者广泛地关注。以字典学习为基础的去噪法在发展中，主要得益稀疏表示的理论进展情况，它基本的思想是通过图像局部的稀疏性实现去噪。

在稀疏在线的字典学习法中，通过在线字典的学习法获取冗余的字典，对算法计算的效率实现了提升。以非局部的自相似去噪法中，基本的思想是通过图像内不相邻的部分具备非局部的自相似来去噪，如NLM的算法(非局部的平均算法)、块匹配和BM3D的算法(3D滤波)等[4]。其中NLM的算法主要借助欧氏距离对像素邻域间相似性表征，且通过此距离对像素重构中的权值计算，从而实现对像素值的估计；BM3D的算法主要对图像块实施匹配，把具有相似性结构二维化图像块的组合共同形成三维化的数据，后对其联合滤波处理，且对重叠块进行加权平均实现图像的重构。此外，一些学者对同时借助稀疏性以及非局部的自相似性图像去噪法进行了研究，还有一些学者通过梯度的直方图进行一致性的约束添加，让去噪后的图像和含噪图像接近，从而对图像的去噪效果提升，但此算法要对图像梯度的直方图事先进行估计[5]。

在上述的算法中，对图像的去噪都获取一定的成功，但此类算法在实现去噪同时也对部分图像的纹理结构相关信息产生了丢失，造成视觉效果的下降情况发生。所以，有必要对既能有效实现噪声去除且还能够对图像细节与纹理信息很好保持的去噪法研究。现阶段，稀疏的表示理论主要集中对稀疏分解以及字典构造的算法等方面研究。若能以此为基础对字典的结构进一步实施优化，对原子的图像表达能力实现提升，降低字典的噪声会对图像产生的影响，将会得到更好的去噪处理效果。

三、基于双正交基字典学习的图像去噪方法

1.以贝叶斯为基础重建图像去噪的模型

对一个噪声的图像考虑：

Y=X+V

(1)

上式内，Y表示所观测的图像；X表示未知原图像；V表示发生叠加零均值型白高斯的噪声。此文章主要的目标是对一个算法自Y中进行噪声删除使它尽可能和原图像X接近的算法[6]。

(2)

在上式内，‖α‖0表示L0的范数，指不是0的元素数量。在稀疏表示中，主要的思想是对图像的信号Y进行成字典内最少一组列的向量分解，它的线性组合所表示信号和Y平方的误差比ε小。 因为上述公式具有组合的性质，在求解中存在很大的困难。现阶段，常用近似的算法有MP(匹配追踪的算法)、OMP(正交匹配的追踪算法)和 BP(基追踪的算法)等。在此文内，采取能够较为简单实现的 OMP方法[7]。

在叠加的零均值型白高斯的噪声y图像块中，其噪声具有标准的方差是σ，所对应原图像x使用上式(2)对稀疏进行表示。通过贝叶斯中最大后验的概率对原图像求解，则对图像块的噪声去除最大的后验估计是：

(3)

(4)

上式内，μ表示正则化的参数，要对其进行合理选取。

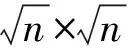
(5)

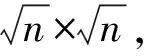
2.以双正交基为基础联合字典的学习法

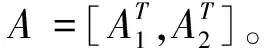
(6)

在上式内，Y所对应的是全部图像块。对上述的优化问题进行直接求解的话，存在很大的困难，所有采用BCR的算法思想对上述问题实施优化处理。此优化处理，可以分作两个阶段，第一阶段通过正交匹配的追踪算法对系数的矩阵A进行确定；第二阶段是固定系数的矩阵A进入到计算的字典D内[9]。此BCR的算法具备收敛性，在对字典D计算阶段中，可先对一正交基固定，后对另一正交基优化计算，这样就能够将式(6)进行下式的转变：

(7)

若假定D2已经固定，则令P等于Y-D2A2，就可以将上式(7)转变为：

(8)

对上式(8)优化的问题就可以进行著名正交普鲁克问题(Procrustes Problem)。

对上式进行优化，对最后一项最大值进行求解，对A1PT奇异值进行分解，得到：

A1PT=U∑VT

tr(D1A1PT)=tr(D1U∑VT)=tr(VTD1U∑)=

tr(Q∑)

由于Q=VTD1U表示正交的矩阵，所以：

在上式内，σii是∑对角的矩阵内第i个的奇异值，而qii是Q矩阵内对角线第i个的元素。若上式达到了最大值，则确定矩阵Q一定是单位的矩阵，Q表示为Q=VTD1U=I，进而得到：

D1=VUT

(9)

在初始化环节中， 令K等于0，且基于噪声图像对图像块级内样本的训练集Z= {Z1，Z2，Z3，… ，ZM}构建，其中M表示样本数；选取两个正交的变换基进行初始化超完备的字典D0构造。

四、基于双正交基字典学习的图像去噪方法验证

对上述的算法性能实施验证，把此算法应用在图像的处理中，常用标准的图像有Peppers、Lena以及Barbara等，选取图像都是512×512的尺寸。对此类图像进行不同噪声的级别白高斯的噪声叠加。用在字典训练以及图像恢复中的图像块具有8×8的像素，对其每个块进行列向量转换而形成实际的信号。

在初始的字典中，选用DCT(离散余弦的变换)、DST(离散正弦的变换)两类正交变换进行合并构建，它们变换完成后的系数比较稀疏。在实验中，设置DCT与DST都是64×64的尺寸，由于字典是64×128的大小。对它们变换的矩阵通过 1D进行变换获取，且大小是8×8，它们的形式表示是：

C1D=cos((i-1)(k-1)π/8)

S1D=sin(ikπ/9)；i，k=1，2，3，...，8。

对它们实施初始化期间，在DCT中除了对第一个原子外其它每个原子就要对其均值减去，从而最终字典是克罗内克积(Kronecker积)，表示为：

C2D=C1D⊗C1D

S2D=S1D⊗S1D

把两字典进行一超完备的DMT字典合并，得到64×128的尺寸。实验中，在学习和去噪过程中都涉及到通过OMP的算法对图像块稀疏表示分解，其终止的条件为平均的误差比T=1.15×σ小，σ表示图像标准的方差，而1.15倍方差终止的条件是通过实验获取的。通过上述算法完成训练后得到Peppers的字典，其训练的次数是10，对噪声的方差是70[11]。

在对算法性能比较中，文章选取现阶段小波域上具有较好效果的去噪法进行比较，主要有BLS-GSM、DMT(非学习性超完备的字典)。对各种的去噪法峰值的信噪比值列出，如下表。

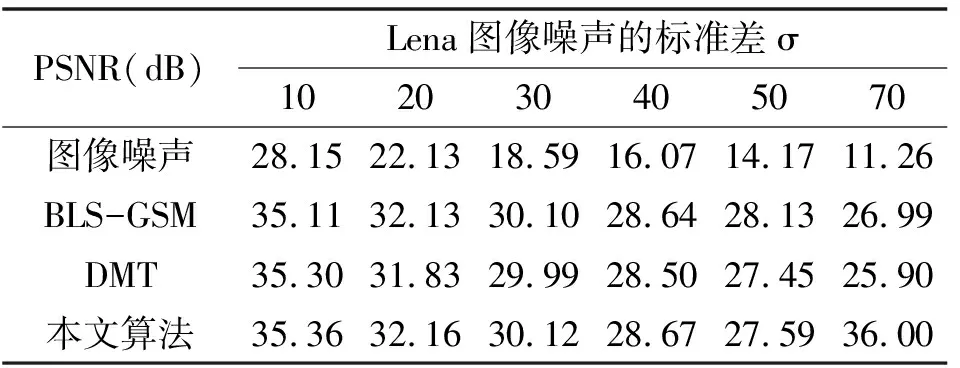
表1 不同噪声的标准差σ下Lena图像不同算法处理后的噪声情况

表2 不同噪声的标准差σ下Peppers图像不同算法处理后的噪声情况

续表2 不同噪声的标准差σ下Peppers图像不同算法处理后的噪声情况

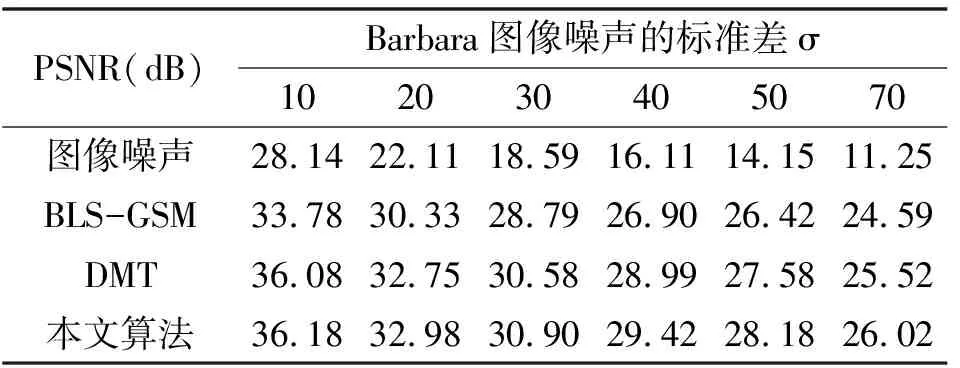
表3 不同噪声的标准差σ下Barbara图像不同算法处理后的噪声情况

通过上表能够看出，基于不同噪声的强度，文章所建立的方法在去噪能力方面比较强，特别是比50dB的噪声条件低的情况。通过文章所研究算法对 Peppers的图像实施去噪，对原图进行标准方差是25噪声的迭加，完成图像的去噪声处理后，噪声已经被基本去掉，呈现出可视的效果十分好。

五、结语

综上所述，文章所提出一种以双正交基的字典学习为基础图像去噪的方法，将图像块当作处理的单元，通过正交匹配的算法对图像块稀疏表示进行计算。将稀疏表示和图像块差当作先验概率的分布，以MAP的框架中去噪图像求解以及字典训练的学习。因为超完备的字典是通过双正交基而构成，所以字典学习的问题就进行 Frobenius(弗罗贝尼乌斯)范式下正交矩阵的求优问题转化，文章给出一种新型推导的公式。因为此问题存在封闭公式的解，所以实现学习速度的有效提升。通过性能实验也表明了，其和传统小波类的去噪法比较，这种基于学习法可以实现对图像内白高斯的噪声更好去除，图像完成去噪后其PSNR值比现阶段较好去噪法小波域要优，且呈现出视觉的效果也更好。