Fluent的高超声速锥形弹丸间的激波干扰研究

王彦超，赵永娟，朱润人，张鹏飞

(中北大学 军民融合创新协同研究院， 太原 030051)

高超声速武器是指飞行速度超过5Ma的武器，目前各国所研制的大部分超高声速武器速度主要集中在6～9Ma之间[1]。飞行器在亚音速和跨音速时激波阻力在总阻力之中的比重较小，而在高超声速飞行时，激波阻力的比重显著提高，因此研究减少激波阻力十分重要。吴子牛等提出的减阻方案包括① 通过物体自身结构破坏激波从而达到减阻的目的。② 通过激波干扰或者反射，使其减弱，或者作用于飞行器背风面，达到减阻效果[2]。关晓辉等[3]提出了基于远场组元的机翼机身协同化优化算法(CoFCE)利用机翼和机身间的气动干扰进行激波阻力的优化。李沛峰等[5]提出了λ形激波激波结构“强干扰”和等熵压缩“弱干扰”的激波减阻控制机理[4]。JIE-MA发现在弹丸肩部安置微叶片抑制弹丸边界层流体分离以提高飞行稳定性。H.Ogawa等[6]提出通过流量控制减少飞行器引起的分叉激振结构从而减小波阻。K.Mazaheri等[7]提出通过激波控制凸起技术(SCB)，改变上游激波结构，进行结构优化。国内外多数以在飞行器上方设置微型凸起破坏激波结构，减阻机构与飞行器为一体结构。本文研究的内容将第一枚弹丸产生的激波作为干扰项，达到对其他弹丸的干扰作用以达到减小阻力，提升升阻比的效果。已达到利用外部干扰所产生的自身空气动力变化实现抛撒弹丸扩大散布面积的目的。目前计算空气动力参数的方法有很多，如牛顿迭代法和极大似然法等[8]。随着科技的发展，空气动力的计算可以更多的借助计算机仿真，利用Fluent以及相关软件，对项目进行仿真计算得出的数据以辅助研究工作。本文基于Fluent，Navier-Stokes方程[9-10]，在黏性存在和绝热壁面的情况下，对双弹头贴近飞行时，计算激波的干扰情况，并在改变密度的情况下得出相应的规律。

1 弹丸飞行的过程控制

本文假设锥形弹丸以7Ma速度飞行时，弹丸头部压缩空气产生激波，当压缩界面作用于后部弹丸激波发生处时的情况，由于常规武器在大气层内的抛撒高度为1 500 m到2 500 m左右，根据海拔高度与空气密度的关系可知，这段区间的空气相对密度为0.858-0.770，于是通过控制空气密度为原有80%再次计算观察其与激波扩散角的关系。

1.1 计算模型的选择

首先对单个弹丸发射时产生的激波位置进行了仿真计算，由于是高超声速飞行，用于不可压缩气体计算的压力体仿真模型，在这里并不适用，改而采取适于可压缩气体的密度体模型。在边界条件设置上采用了速度进口，并设定气流速度为2 380 m/s，出口采用压力出口设定，静压为0，表示出口处与大气压相等。计算中的基本方程包括连续方程、动量方程和能量方程：

(1)

(2)

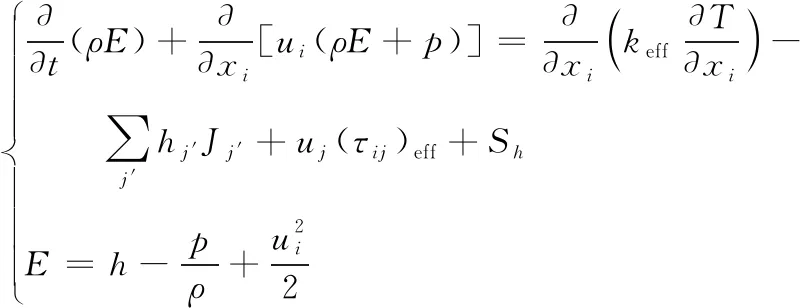
(3)

式中：Sm为分散相附加到连续相的质量；τ为应力张量；δ为张量记号，当i=j时为1，否则为0；keff为有效热传达系数；J为扩散能量；Sh为包括化学反应热的体积热源项；u为在各方向上的速度分量。

在得到结果之后，在软件中，将第2枚弹丸放置在上方，弹头分别与第1枚头部、中部和尾部对齐，以寻找第1枚弹丸激波干扰的最佳位置。通过控制网格最大尺寸小于计算边界1%，在此划分单元长度为边界长度的0.5%的结构化网格，比较适用于方向规律的流体计算，共得到117 215个网格，网格质量较好。网格如图1。

图1 弹丸网格示意图

在湍流模型的选择上主要是以下3种模型：SA模型、k-ε模型和k-ω模型。考虑到边界层的计算与气体扰流，这里选择了双方程模型k-ω的SST，该模型能较好的计算有界壁面和低雷诺数流动，绕流流动，并融合了k-ε公式包含的转捩和剪切方程[11-12]。式中湍流动能k方程和ω方程为:

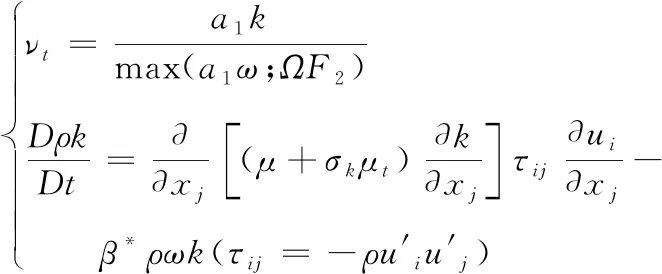
(4)

(5)

式中:Ω为涡量；y为距壁面距离；k为脉动动能；ω为耗散率；γ为重度。

1.2 单弹丸飞行压缩界面的确定

为了确定压缩界面的位置，更好的将被干扰弹丸激波产生位置放置于精确的地点。在正式仿真计算之前进行了单个弹丸的高超声速飞行空气动力仿真计算，并采用了2次计算。这2次除边界条件与上述的情况相同之外，主要区别在于，第1次飞行假定的是在正常近地状态下的标准大气环境温度300 K，大气压力1.013 kPa，大气密度1.293 kg/m3；第2次飞行温度不变，将大气压力和大气密度下调至原来的80%。仿真中以弹头位置为坐标原点，弹头到弹尾的方向为x轴正方向，垂直与x轴向上的方向为y轴正方向。取弹尾正上方激波压缩界面的位置为激波扩张角度的计算点。计算O点的y值与x值的比即tan(A)=Y/X。激波压缩界面示意图如图2。

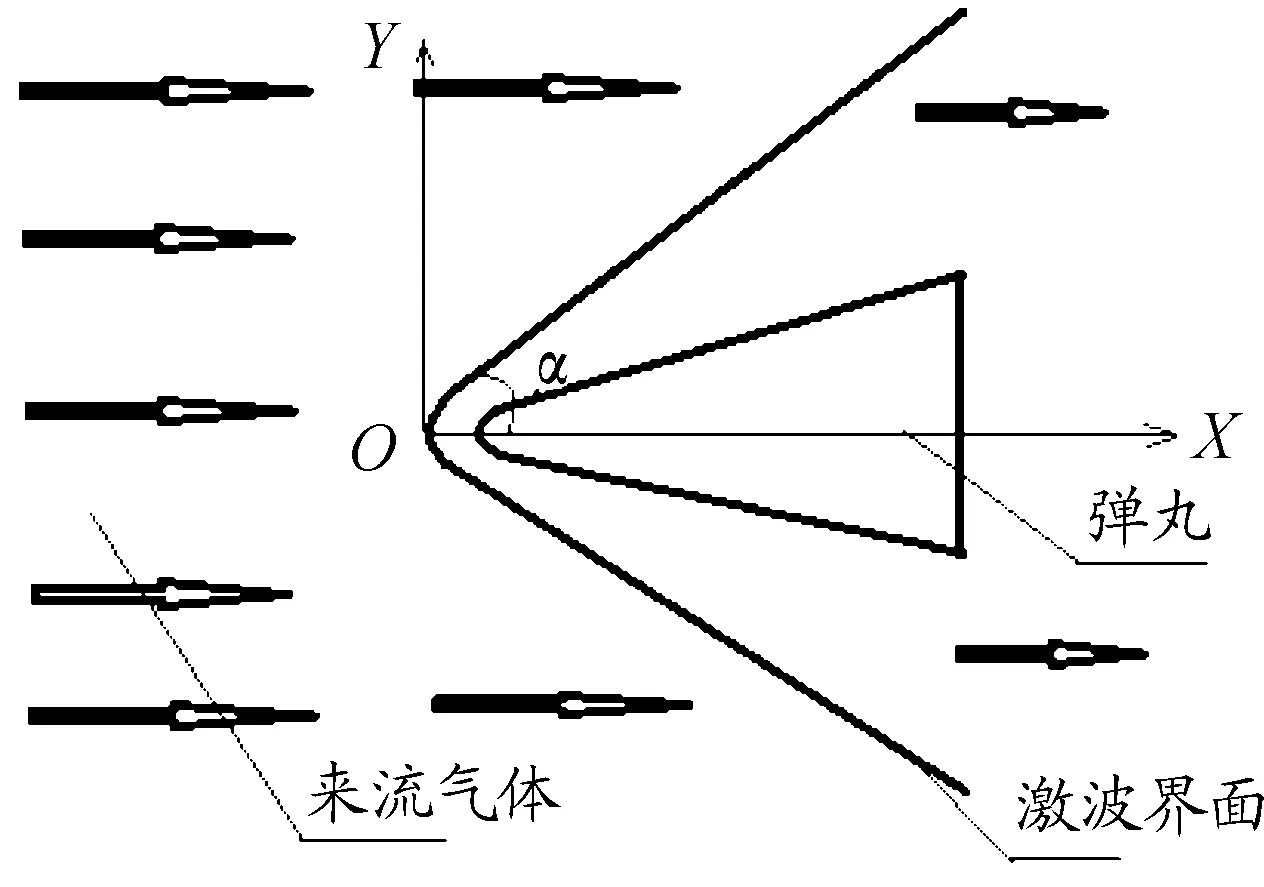
图2 激波压缩界面示意图

经过计算得出在标准大气情况下压缩界面的扩张角A：

tan(A)=0.488

在80%密度的大气情况下压缩界面的扩张角A：

tan(A)=0.619

可以看出在密度和气压降低的情况下，空气表现为更易压缩的状态。在此我们无法得出密度与激波扩张角的具体数值关系。在这里引入脱体激波的概念，即在超声速来流中，钝头物体与波阵面不接触，而是分离的激波，来流气体介质性质与速度的差异，对应一个极限的激波角βmax为：

(6)

式中:M为马赫数；γ为空气的重度，γ=ρg。由于极限激波角是一个定性量，从公式可以看出角度与空气重度有关，而重度与密度和重力加速度有关，重力加速度为常量。从极限激波角的公式可以推断出压缩界面的扩张角正弦的平方与空气密度对应成比例。

2 双弹头飞行激波仿真与分析

首先为了确定前弹丸对后弹丸干扰能达到最佳效果，分别使被干扰弹丸位于干扰弹丸的并列位置，后部半弹长位置和后部全弹长位置进行计算。设置相同的边界条件进行仿真计算得到密度云图如图3～图6：

图3 并列排布密度云图

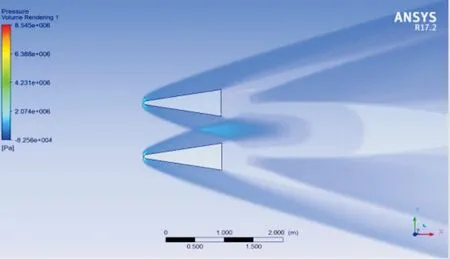
图4 并列排布压力云图

图5 半弹长密度云图

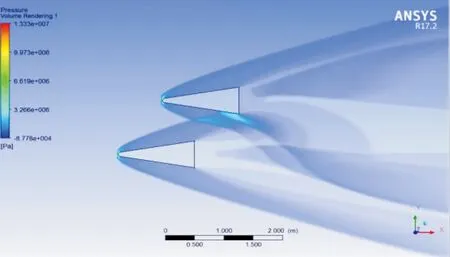
图6 半弹长压力云图

从图中可以看出由于高超声速飞行的原因，激波角度减小，致使干扰较少。在采用传统的并列排布方式的情况下，激波的干扰情况大多数集中于弹丸中间的尾部位置。在后部半弹长度位置的情况下，干扰情况有所增强，也是集中于弹丸的尾部位置。升力系数和阻力系数进行计算得到升阻比的情况，如图7所示。

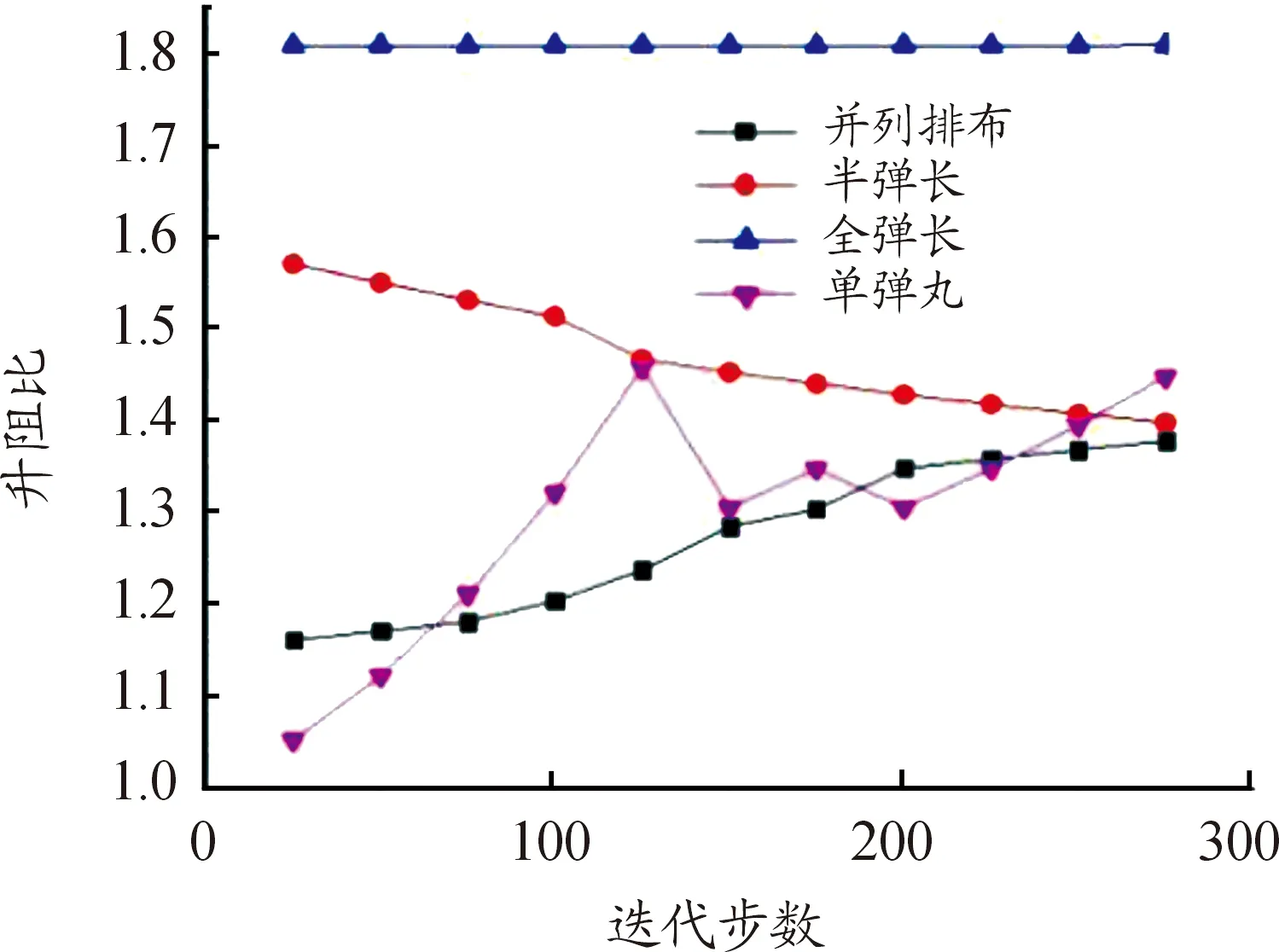
图7 不同位置的升阻比曲线

从图7可以看出，在采取传统的并列排布的方式升阻比基本没有得到提升，在位于干扰弹丸后部半弹长位置的情况下，升阻比有一定的提升，但没有全弹长情况提升明显。仿真结果显示当前弹丸以高超声速飞行时，产生的激波流迹作用于后弹丸的弹头时，对后弹丸的激波产生干扰效果达到最佳。设置边界条件与上文所述相同，共进行两组计算，分别为标准大气密度和80%大气密度。分别得出密度云图，速度云图，温度云图和压力云图如图8～图15。

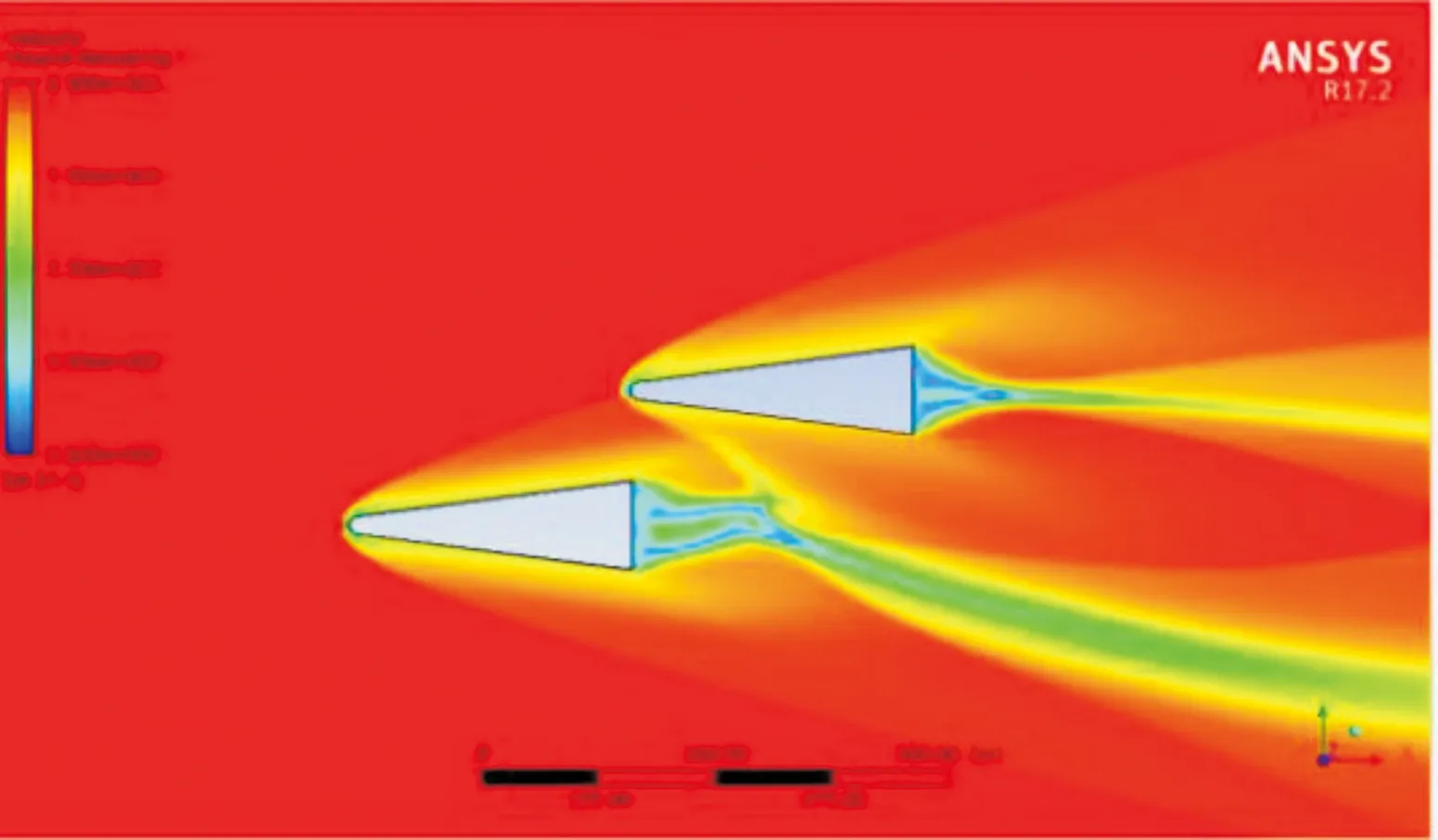
图8 标准密度速度云图

图9 80%密度速度云图

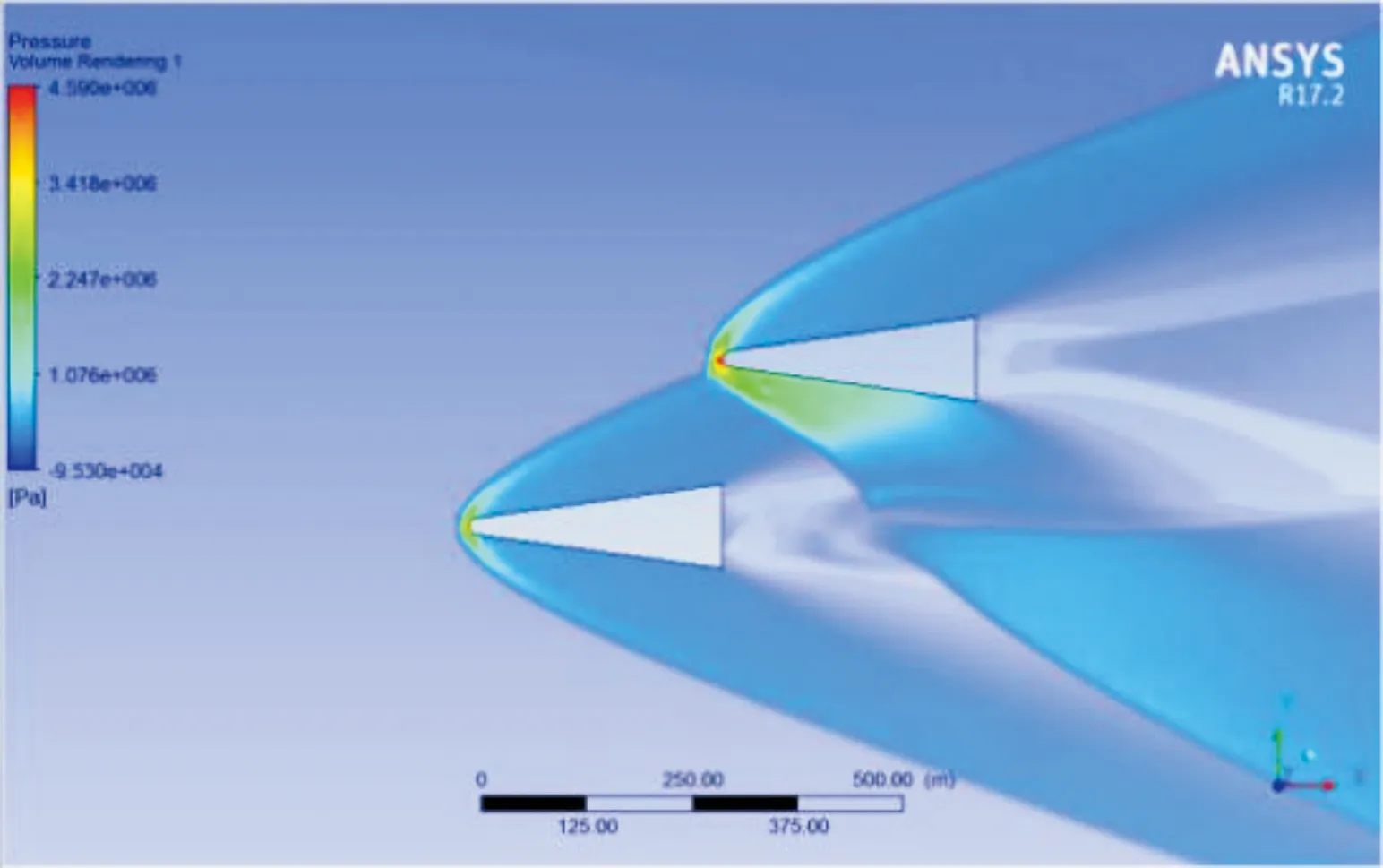
图13 80%密度下温度云图

图14 标准密度下压力云图

图15 80%密度压力云图

分别取未被干扰区域，中间过渡区域和第2颗弹丸下方被干扰区域，3个区域的划分如图16所示。

图16 3个区域的划分示意图

3个区域的速度，密度，温度和压力数值，以标准气压下的气流参数为例求得数据见表1。

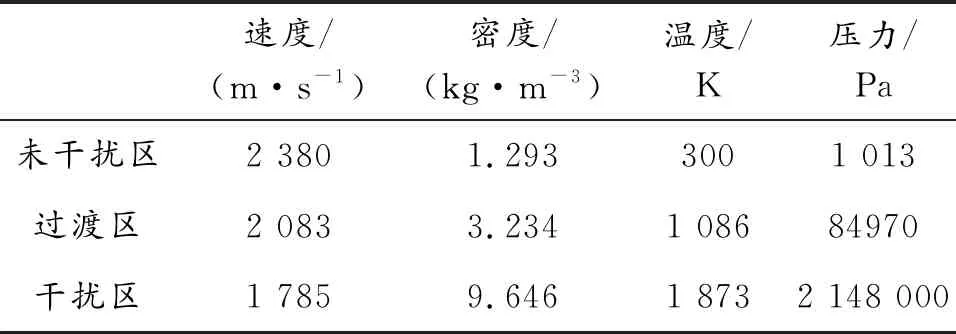
表1 标压下气流数据

通过经验公式可知当空气通过激波时速度下降，密度、温度、压力均上升。其表达式为：

(7)

(8)

(9)

式中k为绝热指数，再通过该公式建立过渡区与干扰区的相关气流公式，并以过渡区为桥梁联立得出未干扰区和干扰区的关系式：

(10)

(11)

(12)

从公式中可以看出未被干扰区和干扰区的压强、密度和温度都与未干扰区和过渡区的马赫数的平方的比值有关。而3部分区域速度的减小量约为300 m/s，接近于1倍音速的衰弱。经过Fluent的仿真计算，分3次对单个弹丸，标压下的双弹丸和80%压力下的双弹丸飞行进行迭代，2次双弹丸飞行监控的都是被干扰弹丸。仿真结束后分别得到了3组情况下的升力系数和阻力系数，选取了数据稳定的一段时间内的系数，并通过作商的方式求出3种情况的升阻比，得到升阻比曲线如图17。

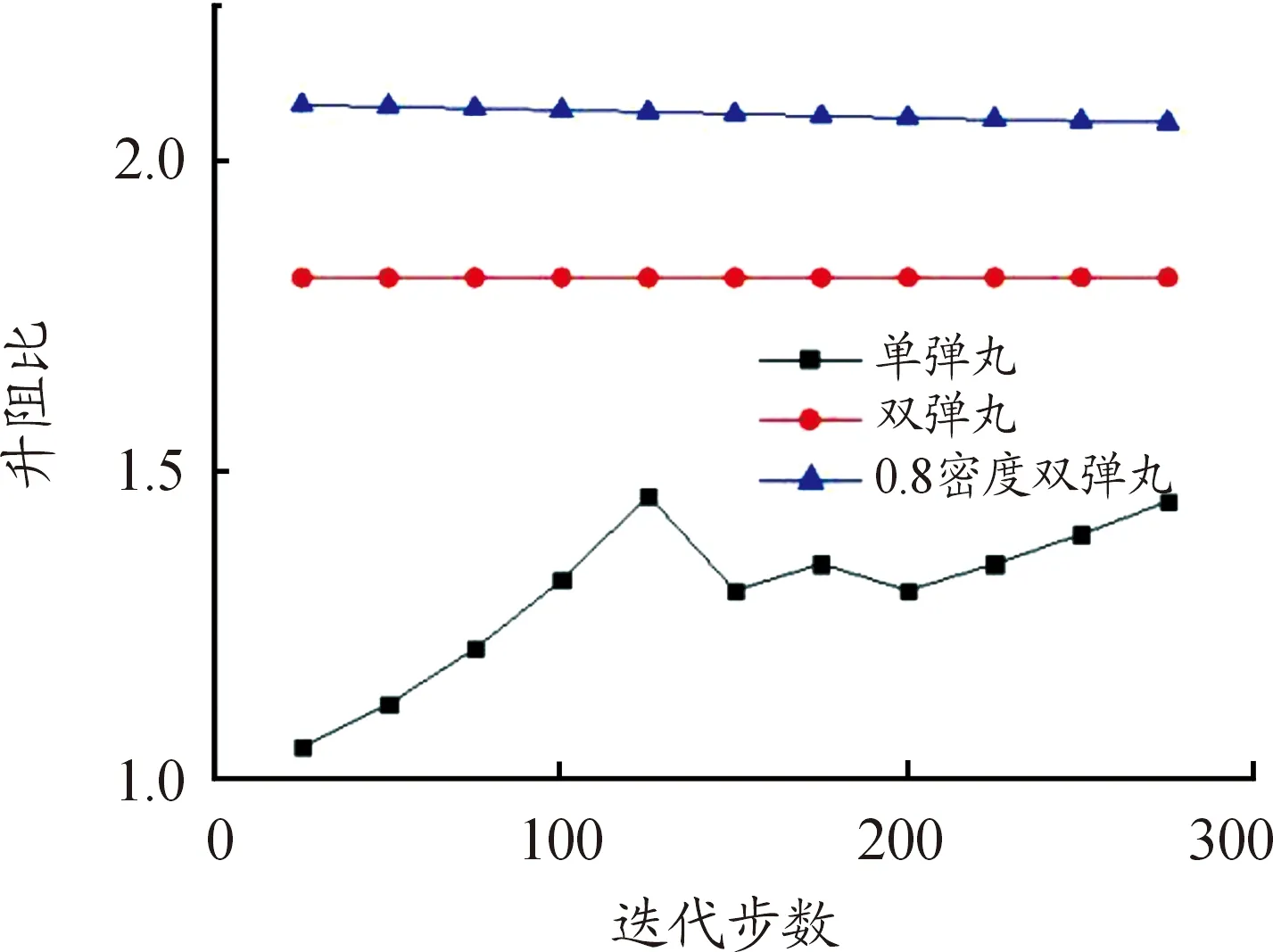
图17 升阻比曲线

随后对所有升阻比数据求和并求取平均值，见表2。

表2 升阻比平均值

从表中可以看出3种情况下的升阻比呈现上升趋势，对于被干扰弹丸，激波的存在对升阻比的提升有着辅助的关系。从第2组和第3组数据中可以看出，密度对升阻比也存在着影响，这可以从Fluent的升阻力系数公式中可以看出：

(13)

(14)

式中：Fs为水平分力；FL为垂直分力，其中ρ对于升力系数和阻力系数的影响是一致的，按照正常计算应该是升阻比不变。然而由于激波干扰的存在，弹体两侧的气流参数已经不同，导致在垂直方向上的分力发生变化，导致了升力系数的提升，进而导致升阻比的提升。

3 结论

利用Fluent对高超声速飞行2个锥形弹丸间激波干扰的情况进行计算。从升阻比的上升趋势可以看出，通过激波的干扰或者反射可以减阻。空气通过激波压缩界面后压力的提升，再经过第2次的提升，使被干扰弹丸两侧的压力分布产生较大差异，压力差作用于弹丸质心，会使两枚弹丸分离。对于多弹头抛撒武器，可以通过位置排布，利用弹丸本身空气动力进行分离，以增大毁伤散布面积。在降低80%密度的情况下，弹丸间的干扰更加明显。整个计算过程符合要求，计算的结果基本达到了预期目的。